FLUENT是常用的空气动力分析软件,软件进行流固耦合分析的计算步骤如下:在每一个时间步内,先求解流体控制方程,得到速度场、压力场以及作用于固体的升力和阻力,通过UDF提取升力和阻力,并结合动力方程计算固体的振动响应,将振动响应中的速度项通过FLUENT动网格宏模块DEFINE_CG_MOTION传递到FLUENT计算数据中,速度与时间步之积即为固体近似的位移响应变化,根据位移响应变化确定固体下个时间步的空间坐标,同时更新固体附近的网格划分,进行下一个时间步的计算(以上参考FLUENT用户自定义函数手册[1])。
由文献[2-4]可知,在FLUENT中流固耦合的计算方法应用广泛,同时可以采用多种数学方法求解运动微分方程(新型显示积分法[5]、四阶Runge-Kutta、Newmark-β算法等),本文着重对采用常加速度Newmark法求解运动微分方程的流固耦合计算方法进行分析。
常加速度Newmark法获取固体的振动响应,振动响应包括位移、速度、加速度,其计算结果是稳定的,同时具有二阶精度[6],因此在时间步长较小的条件下,可以认为这三个振动响应是精确的,然而在FLUENT中采用动网格宏模块DEFINE_CG_MOTION将速度项传递到计算数据中,通过速度与时间步的乘积确定位移响应变化,从而确定新时间步的位移响应,这个位移响应与常加速度Newmark法直接计算得出的位移响应不存在等价性。因此,在FLUENT中,用速度响应结合时间步长计算得出的新位移响应来替代用常加速度Newmark法直接计算得出的位移响应,这样的做法将改变常加速度Newmark法原有的计算过程,是一种近似于常加速度Newmark法的算法(下文将这种算法统一命名为软件算法,同时常加速度Newmark法简称为Newmark法),需要对软件采用的算法流程进行分析,以确定算法流程的可靠性。
本文首先给出数值算例,提出软件采用的算法流程会引入数值阻尼的假定。而后通过数学手段证明数值阻尼的存在,并给出数值阻尼的理论计算公式。之后,给出算例,得出算例的数值阻尼,并利用数值阻尼修正软件采用的算法,同时验证理论公式的有效性。最后,给出文章理论的工程应用。
1 Newmark算法与软件算法算例比较 1.1 算例信息文献[7]阐述了输电塔典型节点钢管构件涡激振动的研究。其中钢管构件直径70mm,壁厚3.5mm,钢管杆件长度在2354mm~3766mm之间,自振频率在7.06Hz~13.36Hz之间。在风洞中改变来流风速的大小,对钢管在空气中涡激振动的现象进行研究。
由于输电塔钢管构件涡激振动现象是在微风下产生的,来流风速较小,其振动由一阶自振频率控制,因此采用单自由度体系进行分析。其力学模型的数学表达式为:
| $ m\ddot x + c\dot x + kx = p\left( t \right) $ | (1) |
式中:k为物体刚度;c为阻尼系数;p(t)为外荷载;x为物体的位移。
为方便分析,对构件的参数进行简化。物体的质量取为m=5.74kg,自振频率取为10Hz,则k取为22660.6N/m,空气密度ρ=1.225kg/m3,来流风速为3.2m/s,迎风面积为0.07m2,阻尼比取ξ为0.015。
在FLUENT中对模型进行分析,获取如下参数:稳定的升力系数CL取为0.7,则外荷载的极值为
由于FLUENT计算量较大,用C语言模拟软件算法的过程,程序借鉴于文献[8]。C语言计算结果经过验证与FLUNET稳定后的计算结果一致,因此下文采用C语言对FLUENT软件的算法流程以及Newmark法的算法流程进行编译计算,并对结果进行比较分析。
根据结构动力学理论[9],当阻尼比不为0时,物体振动振幅公式为:
| $ \rho = {p_0}{k^{ - 1}}{\left[ {{{\left( {1 - {\beta ^2}} \right)}^2} + {{\left( {2\xi \beta } \right)}^2}} \right]^{ - 1/2}} $ | (2) |
式中:p0是荷载最大值,取为0.307N;β为荷载频率与固有频率比,取为0.97。
不同阻尼比条件下,计算结果如表 1所示。
| 表 1 不同阻尼比对应振幅 Table 1 Amplitude of different damping ratios |
|
|
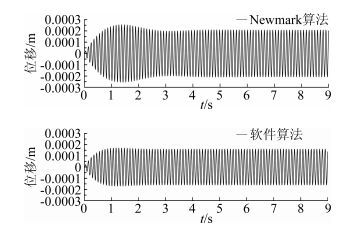
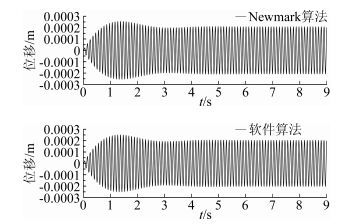
时间步长为0.001s,计算9000个时间步,阻尼为0.015。图 1为阻尼比为0.015时,Newmark算法和软件算法的位移时程图。采用Newmark算法时,稳定的位移最大值为2.07×10-4,与理论值的误差在0.5%以内,可以认为Newmark算法是精确的。采用软件算法时,稳定的位移最大值为1.60×10-4,与理论值的误差在22.3%,软件算法计算误差很大。
|
图 1 阻尼比为0.015时的位移时程图 Figure 1 Displacement-time diagram of damping ratio of 0.015 |
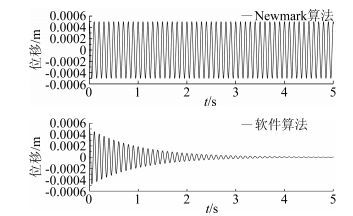
在有阻尼条件下,软件算法比Newmark算法的位移幅值要小的多。结合文献[10]中对数值阻尼的定义(这种阻尼并不是材料本身的内阻尼,而是由于数值计算方法产生的“数值阻尼”,或称为“算法阻尼”),笔者提出在软件算法中引入数值阻尼的假定。为验证以上假定,笔者将分析无阻尼条件下的位移时程图(见图 2)。
|
图 2 无阻尼时的位移时程图 Figure 2 Displacement-time diagram of damping ratio of 0 |
为了显示阻尼经典的衰减特征,在无阻尼算例中,外力为0,初始位移为0.0005m。
在图 2中,采用Newmark算法时,位移没有随着时间出现衰减的现象,证明Newmark算法是不会引入数值阻尼的。然而在采用软件算法时,阻尼为0的条件下,位移随着时间出现了衰减的现象,同时根据阻尼比与位移关系式[9]:
| $ \ln \left( {\frac{{{x_n}}}{{{x_{n + m}}}}} \right) = \frac{{2m\frac{{\Delta t}}{T}{\rm{ \mathsf{ π} }}\xi }}{{\sqrt {1 - {\xi ^2}} }} $ | (3) |
式中:xn、xn+m是物体位移按时间等间距排列后序号为n和n+m的数值,ξ为阻尼比,Δt为时间间隔,T为自振周期。
根据式(3)计算得阻尼比为1.57%。计算得到数值阻尼后,将初始阻尼与数值阻尼叠加,计算叠加后阻尼比的理论位移值(根据式(2)),并与软件算法的数值算例值进行比较,如表 2所示。
| 表 2 考虑数值阻尼后理论位移与数值算例位移比较 Table 2 Comparison of theoretical displacement and numerical displacement considering numerical damping |
|
|
在表 2中总阻尼为初始阻尼与数值阻尼之和。总阻尼比根据式(2)计算得理论位移,并与算例位移进行比较。根据表 2可知,理论位移与数值算例位移拟合性很好,误差在0.9%左右。
因此数值算例验证了软件算法引入数值阻尼的假定,而数值阻尼的最终确定需要用数学方法进行理论证明。
2 算法流程说明 2.1 常加速度Newmark法计算流程说明根据文献[11]给出的常加速度Newmark法采用的基本假定:
| $ {{\dot x}_{t + \Delta t}} = {{\dot x}_t} + 0.5\left( {{{\ddot x}_t} + {{\ddot x}_{t + \Delta t}}} \right)\Delta t $ | (4) |
| $ {x_{t + \Delta t}} = {x_t} + {{\dot x}_t}\Delta t + 0.25\left( {{{\ddot x}_t} + {{\ddot x}_{t + \Delta t}}} \right)\Delta {t^2} $ | (5) |
式中:xt、
为求解t+Δt时刻位移、速度和加速度,引入t+Δt时刻的平衡方程:
| $ m{{\ddot x}_{t + \Delta t}} + c{{\dot x}_{t + \Delta t}} + k{x_{t + \Delta t}} = {p_{t + \Delta t}} $ | (6) |
式中:m、c、k分别为结构的质量、阻尼系数、刚度,pt+Δt为t+Δt时刻的外荷载。
在式(4)(5)(6)中,xt、
1) 根据式(5),用未知量xt+Δt以及t时刻的已知量表示
2) 根据式(4),以及上一步得到的
3) 将前两步得到的
4) 利用xt+Δt和t时刻的已知量求解
5) 此时t+Δt时刻的位移、速度和加速度均为已知,可以进行下一个时间步未知参数的求解。
2.2 软件算法计算流程说明软件算法的前四步和Newmark法一样。然而软件算法在求解得
| $ {x_{t + \Delta t}} = {x_t} + {{\dot x}_{t + \Delta t}}\Delta t $ | (7) |
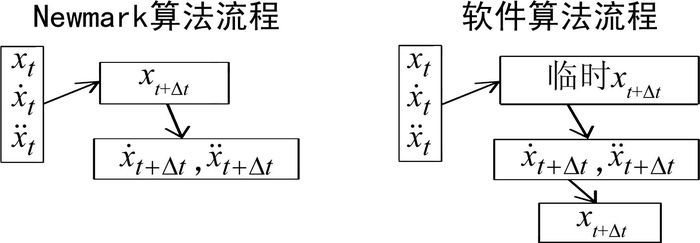
图 3两种算法的流程比较,从中可以看出,软件算法在Newmark算法的基础上,根据式(7)用速度值对位移值进行了修正。
|
图 3 两种算法流程对比 Figure 3 Comparison of both algorithms |
借鉴文献[12]中Newmark法解的稳定性中相关的推导方式,进行软件算法的递推关系式推导。为了避免出现参数表示的歧义,将临时xt+Δt用at+Δt表示。由前面可知数值阻尼与初始阻尼比没有关系,同时外荷载仅仅影响振幅的大小,不会改变数值阻尼,因此在求解通项公式的过程中忽略初始阻尼系数以及外荷载,简化平衡方程式如式(8)。将简化平衡方程式与Newmark算法基本假定式(9)(10)以及修正公式(11)联立,如下:
| $ \begin{array}{l} {{\ddot x}_{t + \Delta t}} + {w^2}{a_{t + \Delta t}} = 0\\ {{\ddot x}_t} + {w^2}{a_t} = 0 \end{array} $ | (8) |
| $ {{\dot x}_{t + \Delta t}} = {{\dot x}_t} + 0.5\left( {{{\ddot x}_t} + {{\ddot x}_{t + \Delta t}}} \right)\Delta t $ | (9) |
| $ {a_{t + \Delta t}} = {x_t} + {{\dot x}_t}\Delta t + 0.25\left( {{{\ddot x}_t} + {{\ddot x}_{t + \Delta t}}} \right)\Delta {t^2} $ | (10) |
| $ {x_{t + \Delta t}} = {x_t} + {{\dot x}_{t + \Delta t}}\Delta t $ | (11) |
将式(8)代入式(9)(10)可得式(12)(13):
| $ {{\dot x}_{t + \Delta t}} = {{\dot x}_t} - 0.5{w^2}\left( {{a_t} + {a_{t + \Delta t}}} \right)\Delta t $ | (12) |
| $ {a_{t + \Delta t}} = {x_t} + {{\dot x}_t}\Delta t + 0.25{w^2}\left( {{a_t} + {a_{t + \Delta t}}} \right)\Delta {t^2} $ | (13) |
将式(13)代入式(12)可得式(14):
| $ {{\dot x}_{t + \Delta t}} = \left( {{a_{t + \Delta t}} - {x_t}} \right)/\Delta t - 0.25{w^2}\left( {{a_t} + {a_{t + \Delta t}}} \right)\Delta t $ | (14) |
将式(14)代入式(11)可得式(15):
| $ {x_{t + \Delta t}} = {a_{t + \Delta t}} - 0.25{w^2}\left( {{a_t} + {a_{t + \Delta t}}} \right)\Delta {t^2} $ | (15) |
式(14)为t+Δt时刻的速度表达式,易知t时刻的速度表达式为式(16):
| $ {{\dot x}_t} = \left( {{a_t} - {x_{t - \Delta t}}} \right)/\Delta t - 0.25{w^2}\left( {{a_{t - \Delta t}} + {a_t}} \right)\Delta t $ | (16) |
将式(16)代入式(13)可得式(17):
| $ \begin{array}{l} {a_{t + \Delta t}} = {x_t} + {a_t} - {x_{t - \Delta t}} - 0.25{w^2}\left( {{a_{t - \Delta t}} + {a_t}} \right)\Delta {t^2} - \\ \;\;\;\;\;\;\;\;\;\;0.25{w^2}\left( {{a_t} + {a_{t + \Delta t}}} \right)\Delta {t^2} \end{array} $ | (17) |
由式(15)易得式(18)(19):
| $ {x_{t + \Delta t}} - {a_{t + \Delta t}} = - 0.25{w^2}\left( {{a_t} + {a_{t + \Delta t}}} \right)\Delta {t^2} $ | (18) |
| $ {x_t} - {a_t} = - 0.25{w^2}\left( {{a_{t - \Delta t}} + {a_t}} \right)\Delta {t^2} $ | (19) |
将式(18)(19)代入式(17)可得式(20):
| $ 2{a_{t + \Delta t}} = {x_{t + \Delta t}} + 2{x_t} - {x_{t - \Delta t}} $ | (20) |
由式(20)易得式(21):
| $ 2{a_t} = {x_t} + 2{x_{t - \Delta t}} - {x_{t - 2\Delta t}} $ | (21) |
将式(20)(21)代入式(15)可得式(22):
| $ \begin{array}{l} {x_{t + \Delta t}}\left( { - \frac{1}{2} - \frac{1}{8}{w^2}\Delta {t^2}} \right) + {x_t}\left( {1 - \frac{3}{8}{w^2}\Delta {t^2}} \right)\\ \;\; + {x_{t - \Delta t}}\left( { - \frac{1}{2} - \frac{1}{8}{w^2}\Delta {t^2}} \right) + {x_{t - 2\Delta t}}\left( {\frac{1}{8}{w^2}\Delta {t^2}} \right) = 0 \end{array} $ | (22) |
式(22)即为软件算法的递推关系式。
3.2 软件算法位移通项式求解根据软件算法位移的递推关系式,利用特征值[13]的方法求解位移的通项式。
由递推关系式(22)可知:
| $ A \cdot \left( {\begin{array}{*{20}{c}} {{x_t}}\\ {{x_{t - \Delta t}}}\\ {{x_{t - 2\Delta t}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} a&b&c\\ 1&0&0\\ 0&1&0 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{x_t}}\\ {{x_{t - \Delta t}}}\\ {{x_{t - 2\Delta t}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_{t + \Delta t}}}\\ {{x_t}}\\ {{x_{t - \Delta t}}} \end{array}} \right) $ | (23) |
式中:a=[1/2+1/8(w2Δt2)]-1[1-3/8(w2Δt2)],b=[1/2+1/8(w2Δt2)]-1[-1/2-1/8(w2Δt2)]=-1,c=[1/2+1/8(w2Δt2)]-1[1/8(w2Δt2)]
求解矩阵A,得矩阵A的三个特征值,记为λ1、λ2、λ3,对应的特征向量分别为V1、V2、V3,则可以推得式(24):
| $ {A^n} \cdot \left( {\begin{array}{*{20}{c}} {{x_t}}\\ {{x_{t - \Delta t}}}\\ {{x_{t - 2\Delta t}}} \end{array}} \right) = \sum\limits_{i = 1}^3 {{c_i}\lambda _i^n{V_i}} = \left( {\begin{array}{*{20}{c}} {{x_{t + n\Delta t}}}\\ {{x_{t + \left( {n - 1} \right)\Delta t}}}\\ {{x_{t + \left( {n - 2} \right)\Delta t}}} \end{array}} \right) $ | (24) |
式中,ci为待定参数,可以根据初始值确定。
由式(24)可以得出软件算法的位移通项式(25):
| $ {x_{t + n\Delta t}} = \sum\limits_{i = 1}^3 {{c_i}\lambda _i^n{v_{1i}}} $ | (25) |
式中,v1i为特征向量Vi第一行的数值。
由数值算例的求解可知,结构振动形式具有周期性,且振幅随着时间的推移出现衰减性,因此特征值λ1和λ2必定为一对共轭复数,同时c1v11=c2v12(保证位移不为虚数,消除虚数项),记λ1, 2=α±βi,并假定物体的初始位移为0(忽略通项式中的第三项),则可以进一步简化式(25),得式(26):
| $ {x_{t + n\Delta t}} = d\left[ {{{\left( {\alpha + \beta {\rm{i}}} \right)}^n} + {{\left( {\alpha - \beta {\rm{i}}} \right)}^n}} \right] $ | (26) |
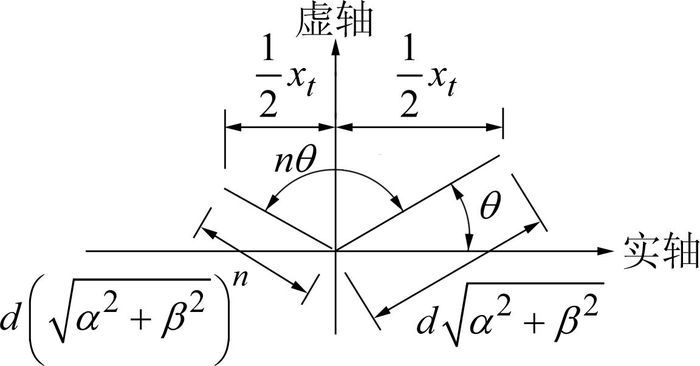
图 4为式(26)复数乘法计算的几何意义。其中θ=arctan(|β/α|),复数的模长在实轴上的投影即为xt+nΔt,在图 4中只显示共轭复数其中一个,因此投影值为实际值的
|
图 4 复数乘法的几何意义 Figure 4 Geometric meaning of multiplication of plural |
根据结构动力学理论[9],位移按e-ξwt衰减,即:在一个周期内,位移将衰减为原来的e-ξw2π/w=e-2πξ。一个周期内,在复平面上,复数需要旋转的次数为2π/θ,投影长度将变为原来的e-2πξ倍,计算式如式(27):
| $ \begin{array}{l} {{\rm{e}}^{ - 2{\rm{ \mathsf{ π} }}\xi }} = {\sqrt {{\alpha ^2} + {\beta ^2}} ^n} + {\sqrt {{\alpha ^2} + {\beta ^2}} ^{2{\rm{ \mathsf{ π} }}/\theta }}\\ \;\;\;\;\;\;\; = {\sqrt {{\alpha ^2} + {\beta ^2}} ^{{\rm{ \mathsf{ π} }}/\theta }} \end{array} $ | (27) |
因此,由式(27)可以推出阻尼比公式:
| $ \xi = - \left( {1/2} \right)\theta \ln \left( {{\alpha ^2} + {\beta ^2}} \right) $ | (28) |
因此,软件算法引入数值阻尼的命题得到证明。
3.4 数值阻尼与采样步长、自振周期的关系由于软件算法将引入数值阻尼,数值阻尼与矩阵A的特征值有关,同时矩阵A中的特征值与矩阵A中行列的数值有关,矩阵A中行列的数值与wΔt有关,因此软件算法引入的数值阻尼仅仅与wΔt相关。
由于wΔt在分析中不直观,因此笔者对wΔt进行如下变换:wΔt=(2π/T)Δt=2π(Δt/T)。Δt为采样时间间隔,T为结构自振周期,该比值直观地反映了单位周期内采样密度,在之后的分析中将采用Δt/T作为主要参数。
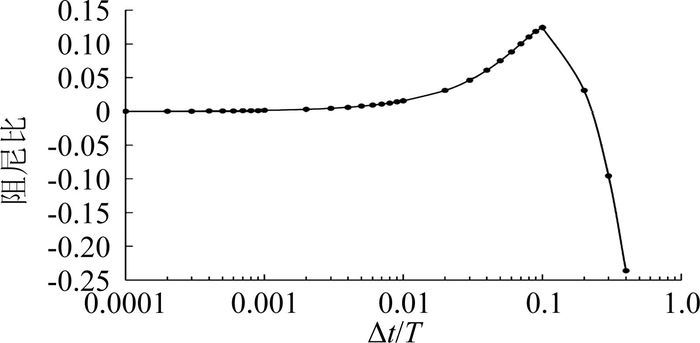
取一系列Δt/T值,计算对应的wΔt值,将wΔt值代入矩阵A,并计算矩阵A的特征值,根据复数特征值实部和虚部大小,结合式(28)计算阻尼比。计算结果如图 5。
|
图 5 阻尼比曲线 Figure 5 Damping ratio |
由图 5可知,当Δt/T小于0.01时,数值阻尼呈现增长趋势,数值计算的结果是稳定的;当Δt/T大于0.3时,数值阻尼为负,数值计算的结果是不稳定的。表 3给出Δt/T介于0.0001~0.01时数值阻尼的大小,从表 3中可以看出数值阻尼随Δt/T的变化是接近线性的,同时若结构初始的阻尼值较小,则数值阻尼将引起较大的误差。
| 表 3 Δt/T介于0.0001~0.01时数值阻尼的大小 Table 3 Numerical damping while the value of Δt/T is between 0.0001~0.01 |
|
|
取前文的数值算例对理论进行验证。易知:Δt=0.001s,T=0.1s,Δt/T=0.01。根据表 3可知,数值阻尼为0.0157,与图 2结合阻尼比与位移关系式计算所得的数值阻尼0.0157一致,说明理论公式的正确性以及精确性。
4.2 利用数值阻尼修正算法软件算法的数值阻尼为0.0157,初始阻尼0.015,因此在实际计算中将初始阻尼扣除数值阻尼,即为-0.0007,将扣除数值阻尼的软件算法记为修正算法。
图 6为阻尼比为0.015时,Newmark算法和修正算法的位移时程图。采用Newmark算法时,稳定的位移最大值为2.07×10-4,与理论值的误差在0.5%以内;采用修正算法时,稳定的位移最大值为2.02×10-4,与理论值的误差在2.0%。
|
图 6 阻尼比为0.015时的位移时程图 Figure 6 Displacement-time diagram of damping ratio of 0.015 |
修正算法计算精度可以满足要求。数值阻尼的理论公式,可以修正软件算法存在数值阻尼的缺陷。
4.3 Δt/T取值范围拓展讨论文章公式主要应用于输电塔钢管构件涡激振动,因此采样频率范围取为每周期20~2000次,可以涵盖实际工程应用,对应Δt/T介于0.0005~0.05。因此,本节中Δt/T讨论的范围为0.0005~0.05。
当Δt/T=0.01时,算例的数值阻尼与理论公式计算所得数值阻尼一致。下面将给出Δt/T取值介于0.0005~0.05时,算例的数值阻尼与理论公式计算的数值阻尼的比较,以进一步验证理论公式的正确性。
在表 4中,算例数值阻尼的获取方式和1.3节无阻尼时Newmark算法与软件算法比较中所用方式一致,均采用假定外荷载为0,初始位移为0.0005m,获取位移衰减时程图,根据公式(3)计算数值阻尼。理论数值阻尼根据表 3获得。
| 表 4 算例数值阻尼与理论数值阻尼比较 Table 4 Numerical damping of cases and theoretical formula |
|
|
由表 4可知,当Δt/T小于0.01时,理论公式的计算误差在1%以内;当Δt/T为0.03以及0.05时,理论公式计算精度下降。计算精度下降的原因如下:采样间隔过大,算法自身计算精度下降,计算精度导致的误差比例上升,导致理论数值阻尼与算例数值阻尼误差加大。
因此,实际应用中,采用理论公式求解数值阻尼并用数值阻尼修正软件算法的必要条件是Δt/T小于0.01。
5 工程应用FLUENT动网格宏模块DEFINE_CG_MOTION在实际工程中被用于模拟空气对弹性体的作用,文献[2-3, 14-15]均涉及动网格宏模块在空气动力学方面的应用。采用本文的数值阻尼理论公式修正软件算法的数值阻尼,可以提高软件的计算精度,对相关的研究工作及工程应用有实用价值。
本文的算例是输电塔钢管构件的涡振,钢管构件涡振由一阶振型控制,因此力学模型采用单自由度体系,之后的理论均是建立在单自由度体系的理论基础上。鉴于以上原因,多自由度体系不在本文考虑之内。考虑其它多自由度结构体系时模型时,因多自由度体系的复杂性,数值阻尼的求解较为困难,笔者建议可以从如下三种方法着手,尝试处理数值阻尼造成的误差:
1) 计算机运行能力足够的条件下,可以采用减小Δt/T比值的方法,减小数值阻尼的影响。
2) 当物体的位移为主要参考变量时,可以返回修正速度,使得修正速度与时间步长计算得的位移为真值,确保位移的正确性。
3) 采用其他的数值积分方法,使得数值积分方法与软件的数据传递模式相匹配。
6 结论1) 利用FLUENT进行空气动力分析,并采用常加速度Newmark法计算物体运动参数时,常用的计算模块是动网格宏模块。动网格宏模块由于自身数据传递方式的限制,修改了常加速度Newmark法的原有算法,引入了数值阻尼。
2) 数学方法证明了数值阻尼的存在,并得出数值阻尼的理论计算公式。软件算法的数值阻尼仅与Δt/T的值有关(Δt为采样步长,T为自振周期),当Δt/T小于0.01时,数值阻尼呈现增长趋势,数值计算的结果是稳定的;当Δt/T大于0.3时,数值阻尼为负,数值计算的结果是不稳定的。
3) 数值算例的验证结果表明:利用数值阻尼理论公式可以修正软件算法存在数值阻尼的缺陷。
4) 实际应用中,采用理论公式求解数值阻尼并用数值阻尼修正软件算法的必要条件是Δt/T小于0.01。
| [1] |
ANSYS Inc. ANSYS FLUENT 14.0 UDF Manual[M]. PA, USA, 2011:181-182.
(  0) 0) |
| [2] |
李田, 张继业, 张卫华, 等. 二维弹性圆柱涡致振动的尾涡模态[J]. 空气动力学学报, 2010, 28(6): 689-695. (  0) 0) |
| [3] |
徐枫, 欧进萍. 正三角形排列三圆柱绕流与涡致振动数值模拟[J]. 空气动力学学报, 2010, 28(5): 582-590. (  0) 0) |
| [4] |
艾尚茂, 孙丽萍, 沙勇, 等. 时间步长对低质量比圆柱涡激振动数值结果的影响[J]. 船海工程, 2011, 40(5): 168-171. (  0) 0) |
| [5] |
翟婉明. 车辆-轨道耦合动力学[M]. 北京: 中国铁道出版社, 2001, 398.
(  0) 0) |
| [6] |
邢誉峰郭静. 与结构动特性协同的自适应Newmark方法[J]. 力学学报, 2012, 44(5): 904-911. DOI:10.6052/0459-1879-12-033 (  0) 0) |
| [7] |
李峰. 输电塔典型节点钢管杆件涡激振动研究[D]. 同济大学, 2008: 57. http://d.wanfangdata.com.cn/Thesis/Y1811706
(  0) 0) |
| [8] |
韩占忠. FLUENT:流体工程仿真计算实例与分析[M]. 北京: 北京理工大学出版社, 2009, 160.
(  0) 0) |
| [9] |
彭津J, 克拉夫R. 结构动力学第二版(修订版)[M]. 盛宏玉, 译. 北京: 高等教育出版社. 2006: 27-30.
(  0) 0) |
| [10] |
方秦, 陈志龙. 显式Newmark法求解波动问题精度的探讨[J]. 岩土工程学报, 1993, 15(1): 10-15. (  0) 0) |
| [11] |
李鸿晶, 王通, 廖旭. 关于Newmark-β法机理的一种解释[J]. 地震工程与工程振动, 2011, 31(2): 55-62. (  0) 0) |
| [12] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003, 491-495.
(  0) 0) |
| [13] |
居于马. 线性代数[M]. 北京: 清华大学出版社, 2002, 223-230.
(  0) 0) |
| [14] |
车竞, 唐硕, 谢长强. 空射导弹发射初始弹道数值仿真[J]. 空气动力学学报, 2006, 23(2): 205-208. (  0) 0) |
| [15] |
朱雄峰, 郭正, 侯中喜. 基于动网格高空长航时机翼优化[J]. 空气动力学学报, 2014, 32(4): 468-474. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


