现代飞行器均布置有多组操纵面,在飞行器设计和制造过程中,操纵面与安定面之间有可能会存在一定的缝隙,缝隙的大小对于操纵效率的影响是操纵面设计的关键问题之一[1]。
飞翼布局飞行器取消了立尾和平尾,以多组操纵面控制飞行,机动飞行时,三轴力和力矩耦合严重,气动力、力矩呈现出明显的非线性特征[2-11],因此操纵面的缝隙对于飞翼布局飞行器操纵特性的影响更大。
目前在飞机设计中主要通过风洞试验[11-12]和数值模拟[12-15]方法确定操纵面缝隙的影响。风洞试验是获取操纵面气动特性的主要方法,但受到模型尺寸的限制,操纵面与安定面之间的缝隙难以准确模拟。数值模拟方法具有周期短、成本低和全尺寸模拟的特点,可作为风洞试验的辅助手段对操纵面缝隙进行设计。
国内对飞行器操纵面缝隙的研究主要集中于舵面缝隙对热流和铰链力矩的影响。陈嘉阳[13]等人对高超声速飞行器舵面缝隙的热流进行了研究,黄宗波[12]等人用风洞试验和数值模拟的方法分析了缝隙对铰链力矩的影响。目前针对飞翼布局飞行器舵面缝隙对操纵性能影响的研究较少,而操纵性能是其操纵面设计中关注的重点问题,进行操纵面缝隙对操纵性能影响的研究十分必要。本文采用数值模拟方法,对某飞翼布局飞行器操纵面缝隙的影响进行了研究,分析了舵面缝隙尺寸对于不同舵面操纵性能的影响。
1 控制方程与数值方法 1.1 控制方程三维非定常可压缩N-S方程在曲线坐标系中的形式[16]为:
| $\frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial \xi }} = \frac{1}{{R{e_\infty }}}\left( {\frac{{\partial {\mathit{\boldsymbol{F}}_V}}}{{\partial \xi }} + \frac{{\partial {\mathit{\boldsymbol{G}}_V}}}{{\partial \eta }} + \frac{{\partial {\mathit{\boldsymbol{H}}_V}}}{{\partial \xi }}} \right)$ | (1) |
式中,Q表示守恒变量矢量;F、G和H分别表示ξ、η和ζ方向的无黏通矢量;FV、GV和HV表示黏性通矢量。湍流的模拟采用两方程k-ω湍流模型。
1.2 数值方法与验证控制方程采用有限体积法求解,黏性通量采用中心差分格式进行离散,无黏通量采用Roe-FDS格式进行离散。远场为无反射边界条件,物面为无滑移条件。
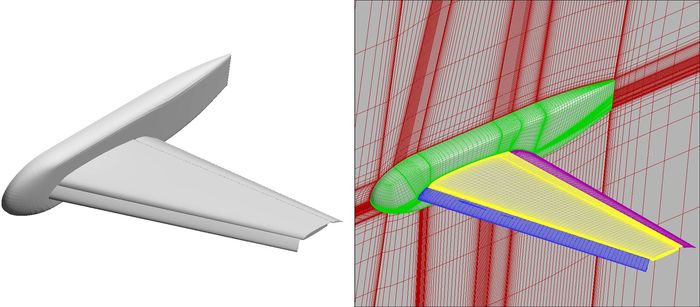
为了验证本文数值方法的精度,选用AIAA HiLift PW-1标模的风洞试验结果[17]。进行对比计算模型和网格如图 1所示,半模网格总数220×106。为准确获取缝隙内的流动,对缝隙区分布了12层网格进行了加密。计算条件见表 1。
|
图 1 DLR-F6计算模型及网格 Figure 1 Calculation model and grid of DLR-F6 |
| 表 1 计算条件 Table 1 Calculation condition |
|
|
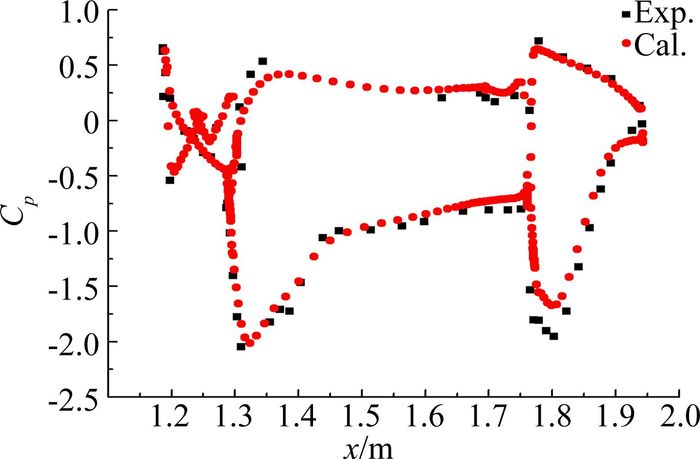
图 2给出了z/b=0.861截面的压力系数与试验值进行对比,其中b为展长。由结果可见,截面压力系数计算值与试验值吻合较好,说明本文的计算方法能够满足分析所需的精度要求,采用本方法进行后续研究可行。
|
图 2 z/b=0.861截面压力系数对比 Figure 2 Pressure coefficient contrast of z/b=0.861 section |
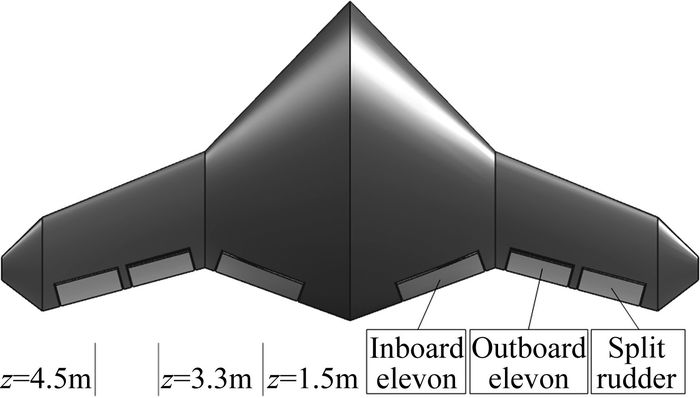
研究对象为飞翼布局飞行器,如图 3所示。该飞行器配置有三组操纵面,分别为内侧升降副翼、外侧升降副翼和开裂式方向舵,内侧升降副翼主要用来控制飞行器的俯仰运动;外侧升降副翼主要用来控制飞行器的滚转运动;开裂式阻力方向舵单侧偏转时控制飞行器的偏航运动,双侧同时偏转时作为减速板使用。
|
图 3 飞翼布局飞行器 Figure 3 Flying wing aircraft |
定义舵面前缘距离主翼面间的最小距离为舵面缝隙,记为h,本文选取三种舵面缝隙,分别为h=0mm、10mm、15mm。舵面的操纵效率定义为有舵偏状态的气动力、力矩系数减去0°舵偏状态的气动力、力矩系数。
采用结构化网格进行研究,为准确捕捉缝隙流动,对缝隙附近网格进行加密,网格总数为2.29×106。计算马赫数为0.6,高度10km,采用俄式坐标系,舵偏正负定义为正舵偏产生负力矩。
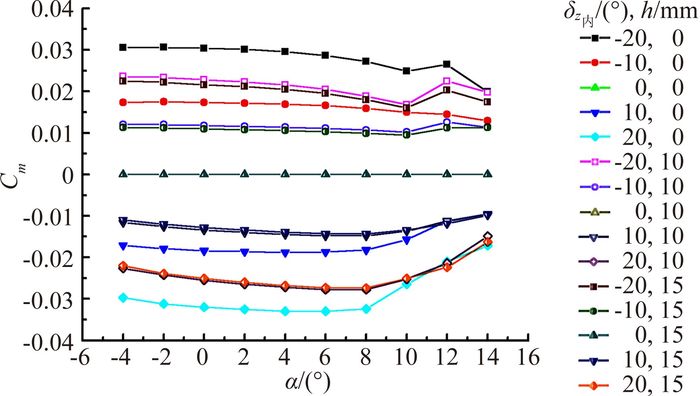
3 计算结果及分析首先针对内侧升降副翼有无缝隙情况下的操纵效率进行分析。图 4给出了内侧升降副翼不同舵偏时操纵面缝隙对操纵效率的影响。
|
图 4 不同缝隙下内侧升降副翼各舵偏的俯仰力矩系数增量 Figure 4 Pitch moment coefficient increment of inboard elevon in different gap sizes |
从图 4可见,相同舵偏角下,内侧升降副翼15mm舵面缝隙的操纵效率比10mm缝隙的操纵效率小2%~7%,10mm舵面缝隙的操纵效率比无缝情况下的操纵效率小16%~33%,且缝隙的存在对负舵偏操纵效率的影响比正舵偏更大。
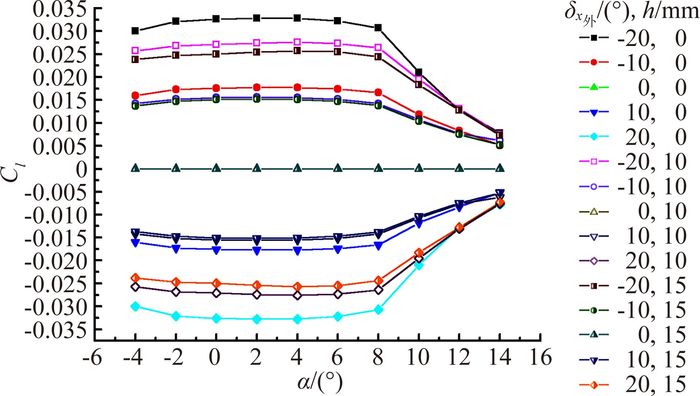
图 5给出了外侧升降副翼作副翼时不同舵偏操纵面缝隙对操纵效率的影响。
|
图 5 不同缝隙下外侧升降副翼各舵偏的滚转力矩系数增量 Figure 5 Roll moment coefficient increment of outboard elevon in different gap sizes |
由图 5可知,外侧升降副翼相同舵偏角下,15mm舵面缝隙的操纵效率比10mm缝隙的操纵效率小3%~7%,10mm舵面缝隙的操纵效率比无缝情况下的操纵效率小12%~17%。
综合来看,相对于舵面无缝状态,10mm舵面缝隙对内侧、外侧升降副翼的操纵效率影响量在12%~33%,15mm舵面缝隙对内侧、外侧升降副翼的操纵效率影响量在14%~38%。
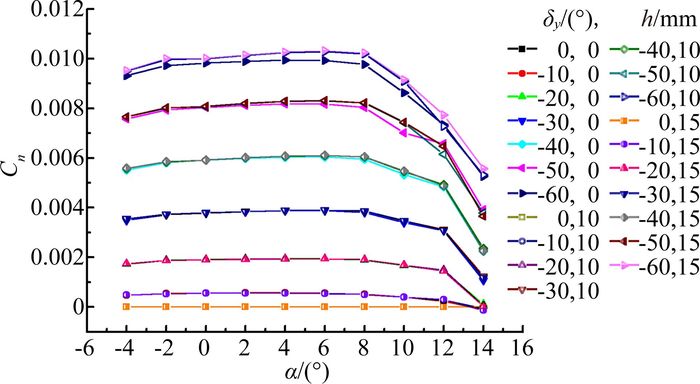
舵面缝隙是否会对开裂式方向舵产生同样的影响?图 6给出了左侧开裂式方向舵偏转时,舵面缝隙对其操纵效率的影响。
|
图 6 不同缝隙下开裂式方向舵各舵偏的偏航力矩系数增量 Figure 6 Yaw moment coefficient increment of split rudder in different gap sizes |
从图 6可以看出,对开裂式方向舵而言,10mm舵面缝隙与15mm舵面缝隙的操纵效率基本一致。与内侧、外侧升降副翼不同,有缝隙存在下的操纵效率比无缝隙的操纵效率高,在40°舵偏角以下这种现象不明显,当舵偏角大于40°,10mm缝隙和15mm缝隙的操纵效率比无缝隙情况下的大2%~5%。
根据上面分析,对于内、外侧升降副翼来说,有缝隙存在时其操纵效率比无缝隙情况低,且缝隙越大操纵效率越低;而对于开裂式方向舵而言,有缝隙存在时的操纵效率比无缝隙高。下面对这种现象产生的原因进行分析。
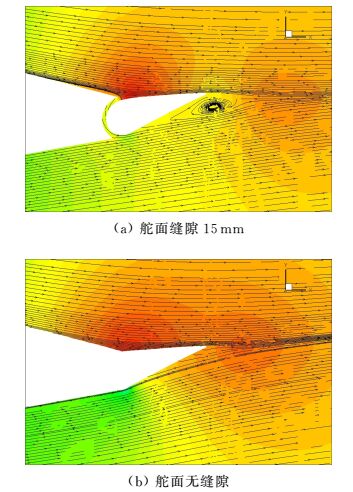
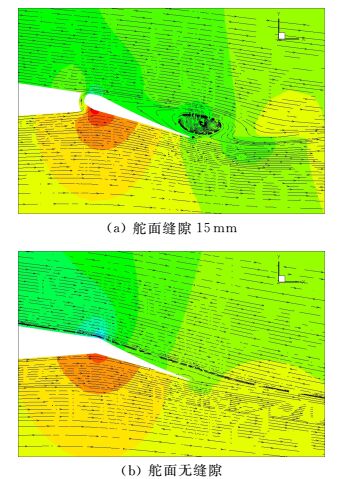
截取距离机身对称面z=1.5m、3.3m和4.5m三个平面,如图 3所示。图 7给出了4°攻角,内侧升降副翼-20°舵偏时z=1.5m截面的压力系数云图和流线图。图 8给出了4°攻角,外侧升降副翼20°舵偏时z=3.3m截面的压力系数云图和流线图。图 9给出了4°攻角,开裂式方向舵60°舵偏时z=4.5m截面的压力系数云图和流线图。
|
图 7 不同缝隙内侧升降副翼-20°舵偏时z=1.5m截面压力系数云图和流线图 Figure 7 Section z=1.5m pressure coefficient contour and streamline plot of inboard elevon deflect at -20° in different gap sizes |
|
图 8 不同缝隙外侧升降副翼20°舵偏时z=3.3m截面压力系数云图和流线图 Figure 8 Section z=3.3m pressure coefficient contour and streamline plot of outboard elevon deflect at 20° in different gap sizes |
|
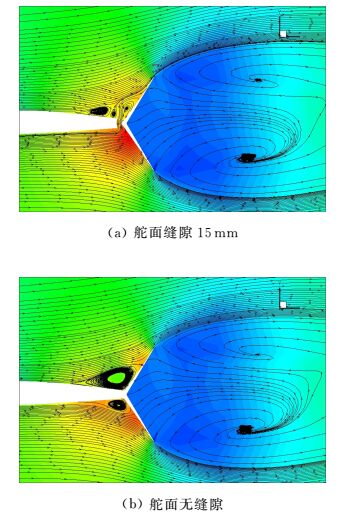
图 9 不同缝隙开裂式方向舵60°舵偏时z=4.5m截面压力系数云图和流线图 Figure 9 Section z=4.5m pressure coefficient contour and streamline plot of split rudder deflect at 60° in different gap sizes |
由图 7~图 9可见,对于内侧和外侧升降副翼来说,缝隙的存在使得上下翼面间存在窜流,舵面压力较高面的气流通过缝隙流入较低面,这样一方面减小了舵面上下表面的压力差,另一方面通过缝隙流入的气流在流出时对主流形成了一定阻滞,造成主流沿壁面法相速度增加,由此引起舵面吸力面的流动出现分离回流,从而降低了舵面的操纵效率。对于开裂式方向舵而言,在舵偏较大时,由于舵面造成的气流阻滞使得上下表面均存在回流区,有缝隙时,下翼面的高压气流通过缝隙加速流动到上翼面,在上翼面回流区内注入了沿舵表面切向的气流速度,使得回流区的范围显著缩小,无缝隙时,上下舵面的回流区更大,而不论缝隙存在与否在开裂式方向舵的后表面均为流动死水区,因而缝隙的存在使得开裂式方向舵在大舵偏时的操纵效率反而有所增加。
4 结论本文通过数值模拟的方法,分析了舵面缝隙对飞翼布局飞行器舵面操纵效率的影响,得到的主要结论如下:
1) 舵面缝隙使得内侧、外侧升降副翼的操纵效率均有所降低,且舵面缝隙越大,操纵效率的降低量越多,15mm舵面缝隙使内侧、外侧升降副翼的操纵效率相对于无缝隙状态降低14%~38%;
2) 舵面缝隙对开裂式方向舵操纵效率的影响与内、外侧升降副翼不同,有缝隙存在时的操纵效率比无缝隙高,且在大舵偏时这种现象更加明显;
3) 内、外侧升降副翼下表面气流通过舵面缝隙流至上表面从而降低了操纵面上下表面的压力差和阻滞了主流并造成吸力面流动分离是其操纵效率降低的原因;有缝隙时下翼面高压气流通过缝隙注入上翼面回流区从而降低回流范围是开裂式方向舵大舵偏时操纵效率增加的原因。
| [1] |
邓克绪. 飞机舵面缝隙设计及其光顺[J]. 南昌大学学报(工科版), 1998, 20(3): 24-31. (  0) 0) |
| [2] |
王睿, 祝小平, 等. 阻力方向舵在飞翼式高空长航时无人机中的应用[J]. 西北工业大学学报, 2008, 26(6): 673-677. (  0) 0) |
| [3] |
王睿, 祝小平, 周洲, 等. 阻力方向舵在飞翼式高空长航时无人机中的应用[J]. 西北工业大学学报, 2008, 26(6): 673-677. (  0) 0) |
| [4] |
Bowlus J A, Multh O D, Banda S S. Challenges and opportunities in tailless aircraft stability and control[R]. AIAA 97-3830, 1997.
(  0) 0) |
| [5] |
Martz C W, Church J D, Goslee J W. Free flight investigation to determine force and hinge moment characteristics at zero angle of attack of a 60°sweptback half delta tip control on a 60°sweptback delta wing at Mach numbers between 0.68 and 1.44[R]. NACA RM-L51I14.
(  0) 0) |
| [6] |
马超, 李林, 王立新. 大展弦比飞翼布局飞机新型操纵面设计[J]. 北京航空航天大学学报, 2007, 33(2): 149-153. (  0) 0) |
| [7] |
赵霞, 秦燕华. 一种飞翼布局横航向特性的控制研究[J]. 空气动力学学报, 2008, 26(2): 234-237. (  0) 0) |
| [8] |
Martz C W, Church J D. Flight investigation at subsonic, transonic, and supersonic velocities of the hinge moment characteristics, lateral control effectiveness, and wing damping in roll of a 60°swept back delta wing with half delta tip ailerons[R]. NACA RM-L51G18.
(  0) 0) |
| [9] |
王磊, 王立新, 贾重任. 飞翼布局飞机开裂式方向舵的作用特性和使用特点[J]. 航空学报, 2011, 32(8): 1392-1398. (  0) 0) |
| [10] |
Gillard W J, Dorsett K M. Directional control for tailless aircraft using all moving wing tips[R]. AIAA 91-3487, 1997.
(  0) 0) |
| [11] |
Grismer D, Grismer M. An experimental investigation of factors influencing hinge moments[R]. AIAA 2000-4016, 2000.
(  0) 0) |
| [12] |
黄宗波, 王勋年, 章荣平. 舵面铰链力矩及其缝隙效应研究[J]. 实验流体力学, 2007, 2007, 21(4): 1-6. (  0) 0) |
| [13] |
陈嘉阳, 阎超. 舵轴缝隙内流的数值模拟研究[C]//第十五届全国计算流体力学会议论文集. 北京: 中国力学学会, 2012: 777-781.
(  0) 0) |
| [14] |
李斌, 刘仙名, 王学占. 战术导弹全动舵舵面缝隙效应研究[J]. 战术导弹技术, 2010(2): 17-21. (  0) 0) |
| [15] |
吴宗成, 朱自强, 丁宁, 等. 三维副翼铰链力矩计算[J]. 航空学报, 2007, 28(3): 519-526. (  0) 0) |
| [16] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006, 17-185.
(  0) 0) |
| [17] |
Rumsey C L, Long M. Summary of the first AIAA CFD high lift prediction workshop[C]//28th AIAA Applied Aerodynamics Conference. Chicago:AIAA, 2011:1-32.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35

