2. 中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 621000
2. High Speed Aerodynamics of Institute China Aerodynamics Research and Development Center, Mianyang 621000, China
静气动弹性表征了气动力和结构弹性力之间的耦合作用,对飞行器的气动性能与飞行安全有着重要影响。例如,在Ma=0.8、Re=2.1×107条件下,弹性变形对MD-90飞机翼身组合体机翼外侧剖面的压力分布影响可达30%以上;波音707飞机在3km高度亚声速飞行时,静气动弹性效应可使飞机焦点前移0.06bA(即机翼平均气动弦长的6%),航向静稳定性导数下降50%[1]。因此,大型飞机的静气动弹性效应问题日益被重视,成为当前飞行器气动弹性专业领域的研究热点之一。
为了准确地预测静气动弹性对飞行器气动性能与结构安全的影响,国内外已经开展了大量的研究工作。在数值模拟研究方面:MSC公司基于不可压无旋流线性Laplace方程发展了NASTRAN等商业软件,波音公司基于跨声速小扰动方程开发了XTRAN3S,NASA基于Navier-Stokes方程耦合模态运动方程研发了CFL3D程序,Ames研究中心专门研发的气动弹性计算软件ENSAERO,都已经被广泛应用于飞行器的静气动弹性计算分析[2-8]。在风洞试验研究方面:比较著名的有美国基于F/A-18A飞机的主动气动弹性翼(Active Aeroelastic Wing, AAW)项目,希望可以主动利用机翼的气动弹性效应达到更好的滚转控制、颤振抑制、阻力减小以及最大可能提升飞行器气动性能[9-11]。在欧洲,瑞典的Martin C对一个大展弦比后掠机翼进行了低速静气动弹性风洞试验,试验基于应变天平测量气动力/力矩,利用光学系统来测量机翼的弹性变形。研究结果表明:随着风速的增加,机翼升力线斜率减小,副翼效率明显降低,机翼沿展向变形明显[12]。在国内,北航的万志强、杨超等人在复合材料前掠翼的发散特性方面进行了相关研究,通过开展低速静气动弹性风洞试验,采用测量结构应变的Southwell亚临界发散试验技术得到前掠翼模型的发散特性[13-14]。沈阳飞机设计所的钱卫与刘钟坤等人在大展弦比机翼静气动弹性模型设计与低速风洞试验方面进行了大量的研究工作,他们所设计的模型满足了几何外形相似与刚度相似的条件,并使模型在大迎角大变形下具备了足够的韧性和强度,且通过低速风洞试验获得了模型的压力系数、升力线斜率与升降舵效率的静气动弹性影响量[15]。
根据文献资料来看,有关飞行器静气动弹性方面的研究主要集中在数值模拟分析与低速风洞试验研究方面。而对于模型设计与制作难度较大、气动特性复杂、风洞试验技术要求更高的大展弦比机翼跨声速静气动弹性风洞试验来说,目前还缺少比较系统的研究。近年来,CADRC高速空气动力研究所针对某大型飞机翼身组合体开展了跨声速静气动弹性风洞试验研究,得到了该模型机翼在Ma=0.65~0.85、q=35~75kPa范围的风洞试验数据,为大型飞机静气动弹性效应的数值模拟方法验证以及风洞/飞行相关性修正研究提供了技术支持。本文简要介绍了试验的相关内容,给出了部分典型试验条件下的静气动弹性效应数据及曲线,对某些典型现象与规律进行了讨论与分析,结果表明由于跨声速阶段大展弦比机翼静气动弹性效应随流动参数变化的复杂性,风洞试验仍将是研究大型飞机静气动弹性效应的有力手段之一。
1 风洞试验 1.1 试验模型风洞试验采用了翼身组合体半模型。机身是刚性的,只提供整流作用;机翼加工两套,一套刚性翼面,一套弹性翼面,比较刚性机翼与弹性机翼气动特性差异,即可获取试验模型的静气动弹性效应[16]。机翼外形为型架构型的“干净”翼面,具备超临界翼型以及大展弦比、后掠、下单翼气动布局特征,忽略短舱/挂架、襟翼滑轨整流罩等。模型及其在风洞中的安装示意图如图 1所示。刚性模型的机身与机翼材质均为30CrMnSiA,试验过程中可认为不变形。弹性机翼材质为高强度复合材料,受到气动载荷后会发生相应的弹性变形。

|
图 1 试验模型外形及风洞安装示意图 Figure 1 Configuration and installation sketch of test model in wind tunnel |
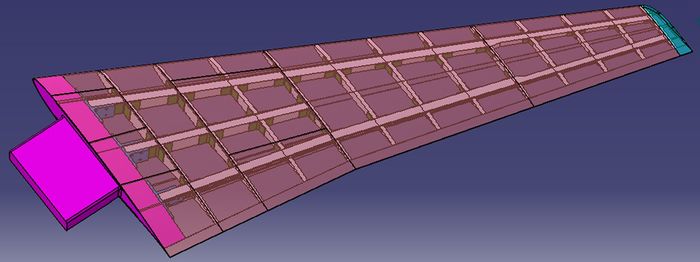
针对弹性机翼而言,为了更精确地模拟结构内部的传力关系,模型设计时参考了真实飞机的结构形式,内部采用梁架结构,外部覆以碳纤维蒙皮。模型除两根大梁外,内翼段中部还有一根短梁及13根肋板与梁架通过角片联接以支撑蒙皮,其余空间填充泡沫维形。弹性模型的结构示意图如图 2所示。弹性机翼除根部接头采用30CrMnSiA材料以外,其余部分都采用的是复合材料。蒙皮采用高强度碳纤维(东丽T300),梁架部分采用高强度玻璃纤维布SW-100A,空隙处用德固赛泡沫(ROHACELL51IG/IG-F)填充维形。与原准模型相比,根据地面刚度试验检测,该弹性机翼模型除翼根局部范围以外,其余测点的柔度矩阵系数误差均小于5%;根据地面模态试验检测,机翼的前四阶主要模态频率误差均小于2%。满足了静气动弹性风洞试验对模型的设计制作要求[17]。
|
图 2 静气动弹性试验模型的内部结构示意图 Figure 2 Internal structure sketch of static aeroelastic test model |
试验在CARDC高速空气动力研究所2.4m跨声速风洞(FL-26)半模试验段中进行。该风洞的详细性能参数见参考文献[18]。
测力试验采用高速空气动力研究所研制的B4W5-200B高精度五分量电阻应变式半模天平,其设计载荷、校准载荷、测量不确定度等详细性能参数见参考文献[19]。
1.3 试验方法本项试验研究采用半模试验方法。为了消除风洞侧壁附面层对模型气动特性的干扰,特意将半模机身的厚度在沿机翼展向靠近安装面的一侧增加了40mm,使半模机身的有效外形曝露于风洞侧壁边界层之外。机身不参与测力,直接与风洞侧壁转窗相连,机翼则通过天平接头与半模天平连接。天平接头包覆于机身内部,如图 3所示。为了防止试验过程中机翼与机身、天平接头与机身相碰而影响测力数据,机翼、天平接头与机身之间通常预留2~3mm的缝隙;为了防止缝隙窜流的干扰,试验前先用硅胶或海绵填充缝隙,再利用强力胶带封严。

|
图 3 机翼与天平装配示意图 Figure 3 Assembling sketch of wing and balance |
静气动弹性风洞试验时,对于弹性模型,试验程序采用固定马赫数、变速压或变迎角的方式进行,风洞速压根据静气动弹性模型设计时确定的速压比换算获得。对于刚性模型,则采用固定马赫数、固定速压、变迎角的方式进行,风洞速压通常选取该风洞各马赫数下的最低速压,以减小试验时模型承受的气动载荷,避免模型发生较大的弹性变形。
2 试验结果分析 2.1 巡航状态的静气动弹性效应分析对于具有大展弦比机翼的大型飞机来说,为了提高气动效率,其巡航Ma通常设定在跨声速区域,而这个范围也正是机翼静气动弹性效应比较严重的区域。因此,静气动弹性对大展弦比机翼巡航状态的气动特性影响值得重点关注。对照飞机的设定巡航飞行状态,根据相似定理换算后,选取对应巡航状态为Ma=0.78、q=35kPa、α=2°。
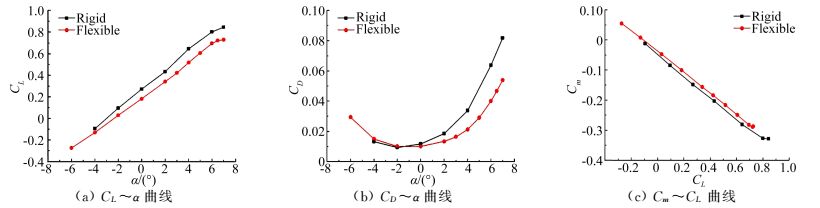
图 4给出了Ma=0.78、q=35kPa时刚性机翼和弹性机翼的CL~α、CD~α、Cm~CL曲线。可以看出,在试验状态范围内,刚性机翼和弹性机翼的气动特性差异明显。也就是说,在巡航飞行状态时,该机翼的静气动弹性效应将明显影响其飞行性能。具体来看,对于升力特性而言,静气动弹性减小了机翼的升力线斜率CLα,根据α∈[-2°~2°]线性拟合求得的CLα计算可知,CLα_F/CLα_R=92.7%(下标“_F”对应于弹性机翼,下标“_R”对应于刚性机翼,以下同),且在巡航迎角α=2°时,升力系数CL大约降低了21%。同时,对比阻力特性曲线可以发现,机翼的零升阻力受静气动弹性影响较小,对阻力特性的影响主要体现在升致阻力大幅降低;在巡航迎角α=2°时,阻力系数CD大约降低了27%。由于升力阻力同时减小,可知静气动弹性对机翼升阻比的影响不及单独对升力或阻力的影响大。经过计算,在巡航迎角α=2°时,升阻比K增加了大约8%。
|
图 4 巡航Ma时的静气动弹性效应 Figure 4 Static aeroelastic effects at cruise Mach number |
Cm~CL曲线反映了机翼的焦点位置或纵向静稳定性裕度,CmCL越小,纵向静稳定性裕度就越大。可以发现,静气动弹性降低了机翼的纵向静稳定性。经过计算得知,CmCL_F-CmCL_R=0.0093,亦即焦点位置XF前移约1%bA。
根据参考文献[20],导致以上现象的原因,主要是由于静气动弹性作用会导致机翼发生扭转变形与弯曲变形,从而改变机翼各翼型剖面(平行于机身纵轴)的有效迎角Δα。Δα的计算方法如下:
| $\Delta \alpha = \varphi {\rm{cos}}\chi - \theta {\rm{sin}}\chi $ | (1) |
其中,φ、θ、χ分别为机翼的弹性扭转角、弹性弯曲角(上反角)以及后掠角。
由于超临界机翼采用上翼面前部“削平”与下翼面后缘加载设计,其设计巡航点的焦点位置一般比较靠后,使得机翼的压心线与刚心线非常接近,加之翼面的扭转刚度很大,因此φ值一般较小,而与机翼弯曲刚度相关的挠度变形却很大,因而θ值较大。于是,Δα值的大小及符号主要取决于θ,而θ是与机翼的升力密切相关的。根据式(1)可知,静气动弹性作用通常会减小超临界大展弦比后掠机翼的有效迎角,从而影响载荷分布,改变其气动特性,从而产生所谓的静气动弹性效应。
2.2 速压对静气动弹性效应的影响分析研究静气动弹性效应随飞行高度和马赫数的变化,是确定飞机飞行包线的重要内容之一。通常,高速静气动弹性风洞试验都是利用变速压来模拟不同的飞行高度,以获取真实飞机的静气动弹性效应随飞行高度的变化特性。定义
| $\Delta x = {x_{\_F}} - {x_{\_R}}$ | (2) |
其中,x表示机翼的某气动系数(导数)。
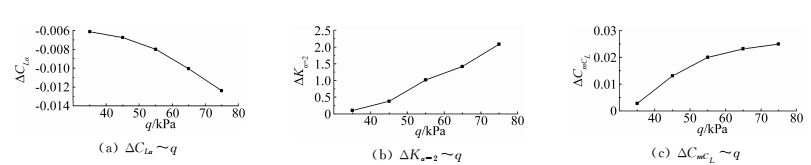
图 5给出了Ma=0.78时的ΔCLα~q、ΔKα=2~q、ΔCmCL~q曲线。总体来看,在Ma=0.78时,机翼的静气动弹性效应随速压并不是表现为简单的线性对应关系,而是呈现出一定的非线性。值得说明的是,ΔKα=2~q曲线在q=45kPa时规律稍显异常,量值偏大,笔者推测应该是由于在α=2°时机翼的轴向力绝对量值较小,天平的测量误差所致。可以看出,在试验状态范围内,机翼的|ΔCLα|与|ΔKα=2|均随着速压的增加而增大,且增长速率随速压增大而加剧;ΔCmCL随速压增加也在增大,但增长速率随速压增大而减缓。因此,以上试验结果表明:在跨声速区域,速压(飞行高度)对大型飞机机翼静气动弹性效应的影响不能简单按照线性规律推测或外插计算,最好是直接通过风洞试验测量或者依据风洞试验结果内插计算来获取。
|
图 5 静气动弹性效应随速压的变化 Figure 5 Dependence of static aeroelastic effects on q |
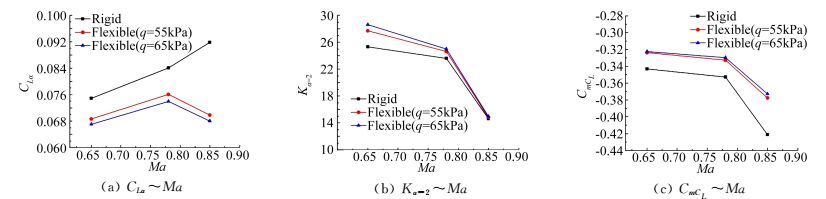
马赫数变化体现了空气压缩性的影响。图 6给出了刚性机翼与弹性机翼的CLα~Ma、Kα=2~Ma、CmCL~Ma曲线。并且,为了表明曲线随Ma的变化特性并非偶然,特意给出了弹性机翼的两组不同速压值下的数据。可以看出,在试验状态范围内,对应于不同的马赫数,刚性机翼与弹性机翼的气动系数/导数除了量值差异较大,其变化规律也不完全一致。例如,刚性机翼的CLα随着Ma的增加而增大,但弹性机翼的CLα随着Ma的增加却是先增大后减小,在Ma=0.85、q=65kPa时,CLα_F与CLα_R相差可达36%,但此时二者的Kα=2却几乎相等。总体上来看,随着Ma的增加,静气动弹性效应引发的升阻比增长趋势减弱,升力线斜率减小趋势增强,静稳定性减弱趋势增强。尤其是在超过设计巡航马赫数以后,静气动弹性效应使得机翼气动特性有恶化的趋势,这主要是由于该机翼的气动优化设计是针对刚性数模来进行的,未对静气动弹性变形后的机翼进行气动优化设计。因此,由于跨声速阶段静气动弹性影响的复杂性,要准确预计大型飞机的气动特性,必须借助于风洞试验或其它更可靠的手段来获取静气动弹性影响量,并进行相应的静气动弹性效应修正。
|
图 6 静气动弹性效应随马赫数的变化 Figure 6 Dependence of static aeroelastic effects on Ma |
基于气动/结构相似的翼身组合体模型,对某大型客机机翼的跨声速静气动弹性效应进行了风洞试验研究,重点探讨了静气动弹性对超临界大展弦比后掠机翼设计巡航点的气动特性影响,以及在跨声速阶段时速压、马赫数对机翼静气动弹性效应的影响。得到了以下主要结论:
1) 在设计巡航点,静气动弹性对超临界大展弦比机翼的气动特性影响明显,可使机翼的升力系数降低21%、升阻比增加8%、焦点前移约1%bA;
2) 在超过设计巡航马赫数以后,静气动弹性效应使得机翼气动特性有明显恶化的趋势;
3) 在跨声速时,马赫数、速压对机翼的静气动弹性效应具有显著影响,且影响规律呈现复杂非线性特征,难以依据现有理论分析手段进行准确预测。
由于大展弦比机翼跨声速阶段静气动弹性效应随流动参数变化的复杂性,利用风洞试验来获取先进大型飞机静气动弹性效应仍将是最有说服力的重要手段,建议在进行飞行器气动/结构设计及优化时,考虑静气动弹性的影响,并基于风洞试验开展技术验证。
| [1] |
陈德华, 林俊, 郭旦平, 等. 大型飞机高速气动力关键问题解决的技术手段及途径[J]. 流体力学实验与测量, 2004, 18(2): 2-5. (  0) 0) |
| [2] |
Rodden W P, Johnson E H. MSC/NASTRAN aeroelastic analysis user's guide[M]. MacNeal-Schwendler Corp, 1994.
(  0) 0) |
| [3] |
Tian B Y. Computational aeroelastic analysis of aircraft wings including geometry nonlinearity[D]. Graduate Education and Research University of Cincinnati, 2003. http://www.openthesis.org/documents/Computational-aeroelastic-analysis-aircraft-wings-533317.html
(  0) 0) |
| [4] |
Zhang Z C, Liu F. Calculations of unsteady flow and flutter by an Euler an d integral boundary-layer method on Cartesian grids[R]. AIAA 2004-5203, 2004.
(  0) 0) |
| [5] |
Livne E, Weisshaar T A. Aeroelasticity of nonconventional configurations:past and future[J]. Journal of Aircraft, 2003, 40(6): 1047-1065. DOI:10.2514/2.7217 (  0) 0) |
| [6] |
Ramji K, Wei S, et al. Time dependent RANS computation for an aeroelastic wing[R]. AIAA 2004-0886, 2004.
(  0) 0) |
| [7] |
Robinson B A, Batina J T, et al. Aeroelastic analysis of wings using the Euler equation with a deforming mesh[J]. Journal of Aircraft, 1991, 28(11): 781-788. DOI:10.2514/3.46096 (  0) 0) |
| [8] |
Guruswamy G P. Unsteady aerodynamic and aeroelastic calculations for wings using Euler equations[J]. AIAA Journal, 1990, 28(3): 461-469. DOI:10.2514/3.10415 (  0) 0) |
| [9] |
Perry B Ⅲ, Cole S R, Miller G D. A summary of the active flexible wing program[R]. AIAA 92-2080, 1992.
(  0) 0) |
| [10] |
Andersen G, Forster E, Kolonay R. et al, Multiple control surface utilization in active aeroelastic wing technology[J]. Journal of Aircraft, 1997, 34(4): 552-557. DOI:10.2514/2.2208 (  0) 0) |
| [11] |
Jennifer H, Charles V S, et al. Experimental results from the active aeroelastic wing wind tunnel test program[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Confer. Austin, Texas, 2005. AIAA 2005-2234.
(  0) 0) |
| [12] |
Martin C. Control surface response of a blended wing body aeroelastic wind tunnel model[C]//41st Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2003. AIAA 2003-1670
(  0) 0) |
| [13] |
万志强, 杨超. 复合材料前掠翼发散亚临界风洞试验方法[J]. 复合材料学报, 2008, 25(1): 200-204. (  0) 0) |
| [14] |
万志强, 唐长红, 邹丛青. 平板前掠翼发散风洞试验预测技术[J]. 复合材料学报, 2002, 19(3): 88-93. (  0) 0) |
| [15] |
刘钟坤, 钱卫. 大展弦比机翼静气动弹性模型设计与风洞试验[C]//第十二届全国空气弹性学术交流会会议论文集, 2011: 268-272.
(  0) 0) |
| [16] |
中国人民解放军总装备部军事训练教材编辑工作委员会. 高速风洞试验[M]. 北京: 国防工业出版社, 2003.
(  0) 0) |
| [17] |
Vasily V C, Fanil Z I, et al. Optimization approach to design of aeroelastic dynamically-scaled models of aircraft[C]//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Albany, New York. 2004. AIAA 2004-4642.
(  0) 0) |
| [18] |
董谊信, 陈章云, 等. CARDC 2.4m引射式跨声速风洞设计与运行调试[J]. 流体力学实验与测量, 2001, 15(3): 54-61. (  0) 0) |
| [19] |
彭超, 谢斌, 陆文祥. 2.4m×2.4m跨声速风洞半模测力天平研制[J]. 流体力学实验与测量, 2001, 15(3): 54-61. (  0) 0) |
| [20] |
郦正能, 程小全, 方卫国. 飞行器结构学[M]. 第2版. 北京: 北京航空航天大学出版社, 2010.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35

