静压传感器是飞机最为重要的大气数据传感器之一,为大气数据计算机计算空速、气压高度等提供静压参数。静压孔是飞机航电系统、飞控系统的重要输入[1],直接关系到飞机飞行性能以及安全。另一方面,静压孔的性能直接关系到空速校准的精度及进度,而空速校准试飞是所有型号飞机试飞的前置科目和基础。随着民机市场日益激烈的竞争,各航空公司对民机性能、运营能力以及飞行安全的要求不断提高,这对静压孔的测量精度提出越来越高的要求。
静压孔目前主要有两种形式,即皮托管式和机身齐平式。皮托管式静压孔布置在皮托管的侧壁,该形式的静压孔受干扰因素较多[2-3],对皮托管的设计、安装位置、静压孔在皮托管上的开孔位置要求很高,在使用时需要通过复杂的补偿对静压进行修正[4-5]。齐平式静压孔安装在机身表面,与机身蒙皮齐平,相对于皮托管式静压孔受气流影响较小。目前在民用飞机领域皮托管式静压孔已逐渐被齐平式静压孔所代替,主流民用飞机均采用齐平式静压孔,如波音B737-800、B737-MAX、B787以及空客A320/330/340/350系列等。即便如此,受机身攻角以及来流速度变化的影响,齐平式静压孔所测静压也可能会与来流静压有一定的差量,我们将此差量称作静压源误差(SSE, Static Source Error)。国军标GJB 1623-93[4]及运输类飞机适航标准CCAR25部[5]对静压源误差及安装提出明确要求,在实际使用过程中一般通过气动补偿对静压源进行修正[4-5]。
静压孔的安装位置直接影响静压源误差,理想的静压孔安装位置会大大降低甚至消除静压源误差。
国外主要飞机制造商针对静压孔安装定位的技术已相当成熟,波音公司、空客公司在此方面都有丰富并系统的经验积累,但作为一项关键技术,很少有静压孔安装定位方面的研究资料公开发表。
国内在静压孔安装定位方面的研究较少。汤黄华[6]通过模型简化,对规则旋成体上静压孔的安装定位进行理论分析,得到旋成体沿径向及周向的理想安装位置。姚宗信等对嵌入式大气数据传感器的测量位置进行研究[7]。其他相关论文主要针对静压源的测量[8-9]、系统设计[10-11]、修正[12]、算法[13-14]以及其他大气数据传感器的安装[15]问题进行研究,缺乏对静压孔安装位置的系统研究。
本文采用CFD计算分析以及简化模型理论分析方法,对静压孔布局规律进行研究。通过均方根统计方法以及圆柱绕流压力系数分布理论分析,以期得到统一的静压孔布局一般规律。开展高低速测压风洞试验对静压孔布局规律进行验证,以证明规律的正确性、普适性。
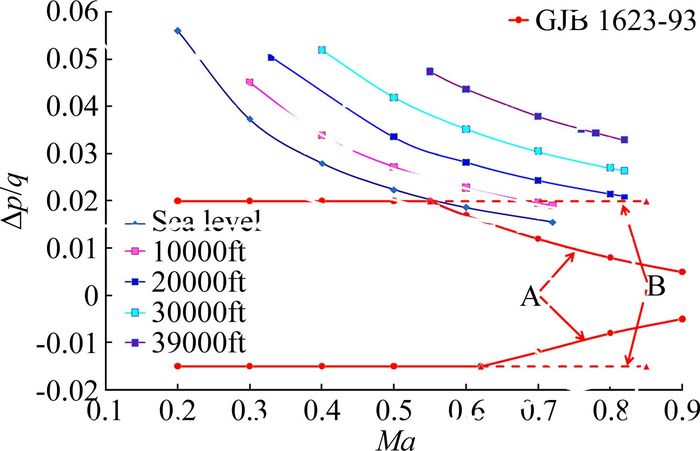
1 设计要求及分析GJB 1623-93《总静压系统设计和安装通用规范》3.2.3节中对静压位置误差提出明确要求:静压位置误差(Δp/q)的容限,当飞机在干净外形和所有重量范围内其容限不应超出图 1的规定。如果位置误差值在曲线B内而不在曲线A内,则必须用大气数据计算机或其他方法进行补偿。若位置误差值完全在曲线A内,可以不用大气数据计算机进行补偿。
|
图 1 静压源误差要求 Figure 1 Requirement of static source error |
运输类飞机适航条例CCAR25-R4 25.1325(e)条也对静压系统的设计及安装主要性能要求如下:每个静压系统的设计和安装必须使在海平面标准大气下所指示的气压高度的误差每100节不超过±10m(30英尺),速度小于100节时,气压高度误差允许为±10m(30英尺)。将要求转换成压力系数误差如图 1所示。
以上是国军标及适航条款对静压源安装的主要要求,其有两方面的含义,首先是理想情况下,飞机全包线范围内静压孔所测静压与来流静压一致;第二方面,工程实际中,允许静压孔所测静压与来流静压存在一定的差量,即静压源误差(SSE),该差量在全包线范围内不超过所指定的量化要求。
根据以上分析,将静压孔安装要求转换成如下两个层次的设计技术指标,即全飞行包线内满足以下要求:
a) Cp=0;
b) Cp误差满足图 1静压源误差要求。
2 气动计算 2.1 计算模型及网格以某支线客机为例,采用翼身组合体模型进行分析。计算网格采用六面体结构网格,网格单元数为8×106,计算模型及相应的网格如图 2所示。

|
图 2 翼身组合体模型及网格 Figure 2 Wing-body model and mesh |
采用三维定常雷诺平均N-S方程对流场进行数值模拟,其控制方程如下:
| $\frac{\partial }{{\partial t}}\iiint_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}V} + \iint_{\partial \mathit{\Omega }} {F\left( \mathit{\boldsymbol{Q}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}S = \iint_{\partial \mathit{\Omega }} {G\left( Q \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}S}}$ | (1) |
湍流模型采用k-w SST两方程模型。
2.3 计算状态根据第1节分析得到的设计技术指标,以及民用飞机的典型飞行状态,确定计算工况如表 1所示。
| 表 1 典型计算工况 Table 1 CFD simulation cases |
|
|
根据第1节中静压孔安装使用要求,期望静压测量值接近于0或者静压源误差修正值SSEC在全飞行包线范围内,静压测量值与0或者SSEC的方差越小越好。
基于以上分析,对机身表面静压测量值与0和SSEC之差的均方根进行分析,在此基础上总结满足技术要求的静压孔布局规律。静压值与0之差的均方根表示为RMS(Cp-0),简写为RMSCp,静压值与SSEC之差的均方根表示为RMS(Cp-SSEC),简写为RMSΔCp,具体分析过程如下。
3.1 RMSCp分布规律根据均方根定义,RMSCp表达式如下:
| $RM{S_{{C_p}}} = {\rm{sqrt }}(\sum {({C_p}\left( i \right) - 0)^2}/n),{\rm{ }}i = 1 \sim n$ | (2) |
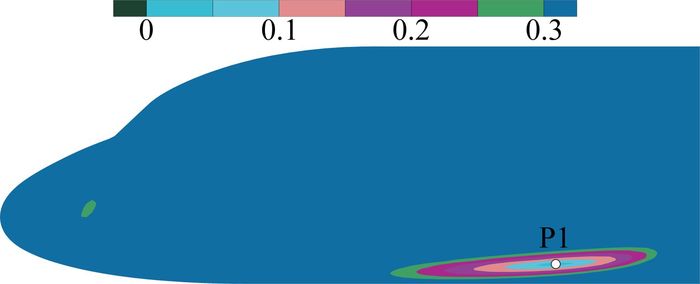
式中Cp(i)表示不同飞行状态下机身表面压力系数,i表示工况序号,n表示工况数。根据式(1)对计算结果进行处理、分析,结果如图 3所示。图 3为所有工况下机身表面RMSCp云图。由图可知:P1点处RMSCp值最小为0.004;满足国军标要求(RMSCp≤0.015)的区域较小,呈长扁椭圆状分布在机身等直段下腹部。
|
图 3 RMSCp云图 Figure 3 RMSCp contour |
与RMSCp相似,RMSΔCp表达式如下:
| $\begin{array}{l} RM{S_{\Delta {C_p}}} = {\rm{sqrt}}(\sum {({C_p}\left( i \right) - SSEC)^2}/n),\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad i = 1 \sim n \end{array}$ | (3) |
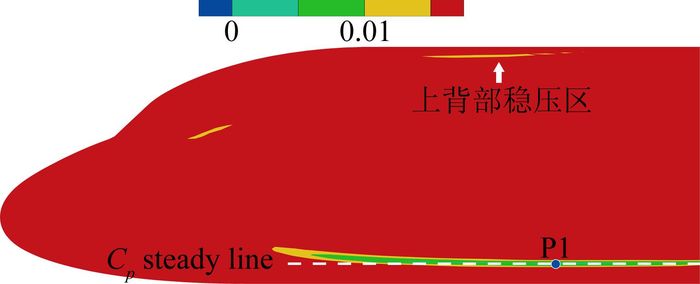
式中SSEC为未知数,在静压孔位置确定之前,无法确定静压源误差修正值SSEC。而本文期望各工况对应静压值与SSEC的相对离散度尽可能小,因此如若有解,理论上可用任意工况的静压值代替SSEC。具体实施时,采用Ma=0、α=0°工况静压值代替SSEC,分析结果如图 4所示。
|
图 4 RMSΔCp云图 Figure 4 RMSΔCp contour |
图 4为所有工况下机身表面RMSΔCp云图。由图可知:RMSCp≤0.015的区域主要以条带状分布在机身等直段下腹部,且该区域在机身周向的相对位置基本保持不变,如图中白色虚线所示,本文将其定义为稳压线。稳压线上Cp随α、Ma数变化较小,同时P1点位于稳压线上。还有很小的一部分分布在机身上背处,由于工程实际中静压孔面板不能朝上,因此不对上背部稳压区进行分析。
3.3 静压孔布局规律根据以上对机身表面RMSCp和RMSΔCp分布规律的分析,可得到理想静压孔安装位置规律如下:P1点是最佳静压孔安装位置;稳压线是扩展最佳安装区域。
工程实践中,最佳安装位置的P1点可能无法实现,而作为扩展最佳安装区域的稳压线则更具有工程实践意义。下面对稳压线相对位置进行分析,以期获得更为具体的静压孔理想安装位置规律。
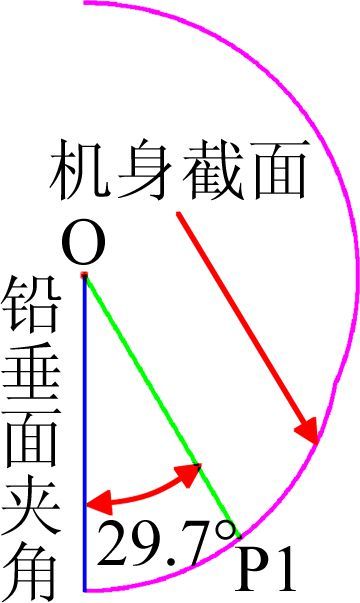
如图 5所示。P1点位于机身下半圆,其与圆心O的连线OP1与飞机对称面的夹角为29.7°,即这是P1点及稳压线沿机身周向的具体位置。该规律仅针对本文构型有效。
|
图 5 稳压线相对位置分析 Figure 5 Cp steady area analysis |
根据Cp均方根统计所得到的稳压线结果提示,在机身等直段存在一个区域,Cp随α、Ma数变化较小。本节将通过简化模型理论分析,以期得到相似的规律,以证明该规律的普适性。
4.1 模型简化稳压线分布在机头之后、机翼之前的机身等直段,将这段机身等效成圆柱体,同时将该区域的流动分解成圆柱轴向的平直流动和周向的绕流,如图 6所示。下面分别就周向绕流速度分量Vv和轴向流动速度分量Vh对圆柱表面的压力分布影响进行分析,具体如下。
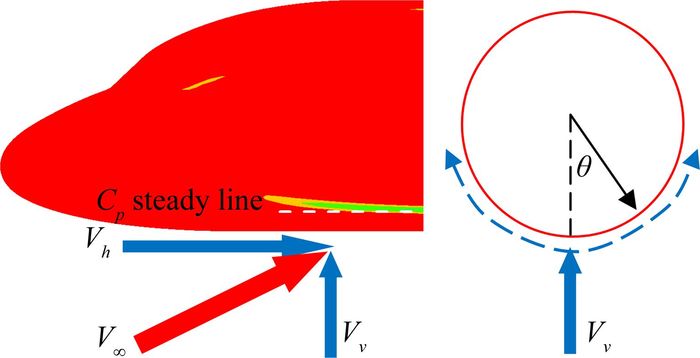
|
图 6 速度分解示意图 Figure 6 Velocity decomposition |
理想情况下,圆柱绕流表面压力分布可表示为:
| ${C_p} = 1 - 4{\rm{si}}{{\rm{n}}^2}\theta $ | (3) |
式(3)为无黏不可压时圆柱表面的压力系数。其中,θ为圆柱迎风面相对于前缘驻点角坐标。
假设圆柱体上存在一条母线,其上静压值不随来流速度变化而变化,即Cp·q=常数,其中Cp为母线上的压力系数,q为来流动压。
由于来流速度是变化的,即q是变化的,因此当且仅当Cp=0时,Cp·q=常数。
令Cp=1-4sin2θ=0,解得θ=±30°、±150°,即与来流夹角成30°、150°、210°、330°的母线上静压值不随来流速度变化而变化,且其静压等于0。
以上结论仅适用于无黏不可压情况。而根据Rodriguez[16]、许常悦[17]等人的研究,当θ<60°或θ>300°时,表面压力系数受黏性及压缩性影响较小,Cp分布和理论解近似;60°<θ<300°时,受黏性及压压缩性影响,与理论解差异较大。因此,考虑到黏性及压缩性影响,本文中θ=±30°的母线即为稳压线,该结果与3.3节中所得到的结果29.7°高度一致,且为通用规律。而θ=±150°时对应机身上背部小范围稳压区。
4.3 轴向流动影响根据周向绕流分析结果,在没有轴向流动时,图 4中稳压线上所有位置处的Cp=0。当有轴向流动存在时,受机头以及机翼影响,轴向流动对稳压线上Cp绝对值有一定影响。图 4中P1点在稳压线上的相对位置即为轴向流动影响的结果,但对稳压线上Cp相对变化影响较小。
4.4 理论分析结论通过以上对圆柱体表面周向及轴向流动的理论分析,得到以下结论:稳压线位置与CFD计算结论一致,且是周向绕流作用的结果;P1点在稳压线上的相对位置是轴向流动作用的结果。
5 风洞试验验证通过CFD计算以及理论分析,得到机身静压孔的理想安装位置——P1点及Cp稳压线,即机身等直段下表面相对于对称面角坐标为±30°的母线。继续通过高低速测压风洞试验,进一步验证该规律的正确性。
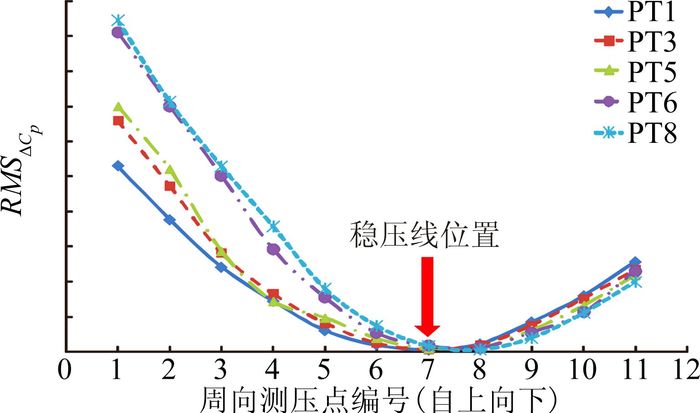
试验模型如图 7所示。测压孔呈11×8矩形分布在Cp稳压线附近,周向分布11个测压点,稳压线上的测压点位于第7点;轴向分布8个测压点,PT6为静压孔最佳安装位置P1。试验结果如图 8~图 10所示。

|
图 7 风洞试验模型及侧压孔位置 Figure 7 Wind tunnel experiment model |
|
图 8 所有状态RMSΔCp风洞试验结果 Figure 8 Experiment results of RMSΔCp |
|
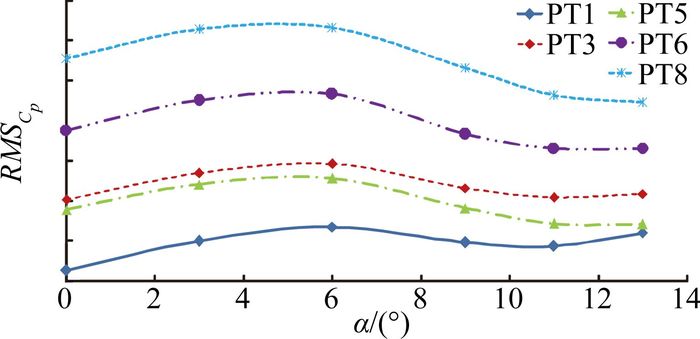
图 9 RMSCp低速风洞测压试验结果 Figure 9 Low speed experiment results of RMSCp |
|
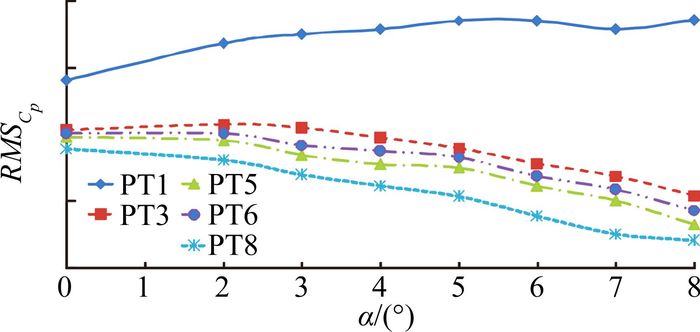
图 10 RMSCp高速风洞测压试验结果 Figure 10 High speed experiment results of RMSCp |
图 8为所有试验状态下RMSΔCp风洞试验结果,横坐标为周向每一列测压点的序号。由图可知,周向第7点及稳压线附近RMSΔCp最小,试验结果进一步验证稳压线规律的正确性。
图 9~图 10为每一列7号测压孔即稳压线上高/低速风洞试验结果。由图可知,稳压线上Cp随攻角的变化规律基本一致; 低速试验Cp相对变化范围在0.015以内,高速试验Cp相对变化范围在0.004以内;PT6(P1)处的Cp绝对值最小。高/低速风洞试验所得结论与CFD计算及理论分析结果一致。
综合高/低速风洞试验结果,稳压线上Cp相对变化范围最小,满足静压孔安装使用要求;PT6(P1)处Cp绝对值最小,且满足静压孔安装使用要求,是最理想的静压孔安装位置。试验结果进一步验证CFD计算以及理论分析结果的正确性。
6 结论本文通过CFD计算分析以及理论分析对民用飞机静压孔安装定位规律进行研究,并通过风洞试验进行验证,得到如下结论:
1) 通过Cp均方根分析方法以及圆柱绕流Cp分布理论分析,得到一致的静压孔布局一般规律,即稳压线:Cp随来流速度、攻角变化很小,且满足静压孔安装使用要求;
2) 通过高/低速风洞测压试验,对稳压线规律进行验证,结果表明稳压线规律正确、普适;
3) 本文所得稳压线分布规律可为常规布局民用飞机静压孔布局提供直接参考;
4) 本文提出的均方根分析方法以及圆柱绕流Cp理论分析方法可为其他类型飞机静压孔的安装定位提供方法借鉴。
| [1] |
黄凤华, 王玲. 先进控制技术的主要控制方法综述[C]//第十九届电工理论学术年会论文集, 2007.
(  0) 0) |
| [2] |
孙志强, 周孑民, 张宏建, 等. 皮托管测量影响因素分析Ⅱ.全压孔与静压孔的影响[J]. 传感技术学报, 2007, 20(4): 941-944. (  0) 0) |
| [3] |
王敏, 周树道, 王彦杰, 等. 影响皮托管测风精度的几个因素[J]. 实验室研究与探索, 2010, 29(3): 35-37. (  0) 0) |
| [4] |
CCAR-25-R4运输类飞机适航标准.中国民用航空规章[S]. 2011.
(  0) 0) |
| [5] |
CCAR-25-R4运输类飞机适航标准. 中国民用航空规章[S]. 2011.
(  0) 0) |
| [6] |
汤黄华. K8飞机机身静压盘的选位安装[J]. 洪都科技, 1999(3): 16-20. (  0) 0) |
| [7] |
姚宗信, 梁大开, 李明. 基于模糊逻辑的嵌入式飞机大气数据传感器测量位置优化设计[J]. 计量学报, 2004, 25(3): 257-261. (  0) 0) |
| [8] |
孟博. 跨声速/高超声速大气数据测量技术研究[D]. 南京航空航天大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10287-1011292036.htm
(  0) 0) |
| [9] |
欧雷. 大气数据测量不确定度评定[C]//2007年度中国航空学会计量技术专业委员会计量与质量专题学术交流会, 2007.
(  0) 0) |
| [10] |
钱默抒, 熊克. 无人机大气数据检测系统的设计[J]. 桂林电子科技大学学报, 2006, 26(2): 97-99. (  0) 0) |
| [11] |
张小平, 宋振宇. 大气数据自动测控系统设计[J]. 海军航空工程学院学报, 2008, 23(3): 66-68. (  0) 0) |
| [12] |
孟博, 李荣冰, 刘建业, 等. 基于改进反向传播算法的跨声速攻角补偿修正研究[J]. 系统工程与电子技术, 2010, 32(12): 2681-2685. DOI:10.3969/j.issn.1001-506X.2010.12.38 (  0) 0) |
| [13] |
邵笑杰. 嵌入式飞行数据传感系统的算法研究[D]. 南京航空航天大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10287-2005079259.htm
(  0) 0) |
| [14] |
李其畅, 刘劲帆, 刘昕, 等. 嵌入式大气数据三点解算方法初步研究[J]. 空气动力学学报, 2014, 32(3): 360-363. (  0) 0) |
| [15] |
赵克良, 周峰, 张淼. 民用飞机攻角传感器安装定位研究[J]. 空气动力学学报, 2015, 33(3): 420-426. (  0) 0) |
| [16] |
Rodriguez O. The circular cylinder in subsonic and transonic flow[J]. AIAA Journal, 1984, 22(12): 1713-1718. DOI:10.2514/3.8842 (  0) 0) |
| [17] |
Xu C Y, Chen L W, Lu X Y. Effect of Mach number on transonic flow past a circular cylinder[J]. Chinese Science Bulletin, 2009, 54(11): 1886-1893. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35

