2. 西南科技大学制造科学与工程学院, 四川 绵阳 621000
2. School of Manufacturing Science and Engineering, Southwest University of Science and Technology, Mianyang 621000, China
结构网格具有边界层模拟准确、计算效率高等优势,因此它在当前的CFD研究和工程应用中仍然被大量采用[1-5]。在气动优化设计[6]以及气动弹性等多学科耦合[7-9]计算过程中,经常会遇到外形剧烈变化的情形,这给结构网格自动生成提出了巨大的挑战,即必须处理好复杂外形表示以及网格自动生成两个问题。
对于网格自动生成方法,比较常用的有网格变形法[10-12]、嵌套网格法[13]、网格重构法[14]和浸入边界法[15-16],在此重点关注网格变形法[17-21]。基本的网格变形法包括超限差值法[10]、弹簧法[11]、Delaunay背景网格插值法[17]、径向基函数插值法[18]等。在传统的网格变形技术中,基于插值法的代数变形技术计算时间开销相对较少,但仅限于小幅度的网格变形;弹簧法等迭代变形技术能处理大位移运动,但是计算时间开销比较大。
针对传统网格变形技术无法有效处理剧烈变化外形的问题,本文提出了一种基于网格框架的结构网格重构方法,其基本思路是:首先,从初始多块对接结构网格提取拓扑结构信息,仅保留还原网格拓扑所必需的线/面数据,从而得到初始网格的网格框架;然后,用宜于变形且能较好保证变形时网格品质的样条拟合曲线替换网格框架线;最后,对新网格框架线实施变形,借助变形后的网格框架重新构造变形后的网格。
1 网格框架 1.1 网格框架概念在CFD应用中,网格是指按特定规律离散计算空间而形成的离散点集以及它们的相互关系。组成网格的元素包括网格点、网格线、网格面、网格体及其关联关系。在此,将多块分区结构网格中界定各网格块、确定网格拓扑结构的网格线或网格面称为网格框架。
相对于整个网格中结构精细、关系严谨的网格单元,网格框架具有更粗放的结构、更大的变形空间以及更强的外形变形适应能力。在保证网格拓扑结构不变的前提下,网格框架原则上可以适应任意的物面变形:根据它所保存的网格数据关系,利用变形后的网格框架重新生成新的结构网格,从而实现结构网格在物面变形后的自适应重构。
1.2 网格元素关系信息表示对于三维结构网格,其网格框架可由二维网格面或一维网格线构成;前者构成的网格框架结构相对简洁,而后者构成的则可以灵活处理物面变形问题。为更好地适应物面变形网格的重构问题,此处根据一维网格线来构造网格框架。
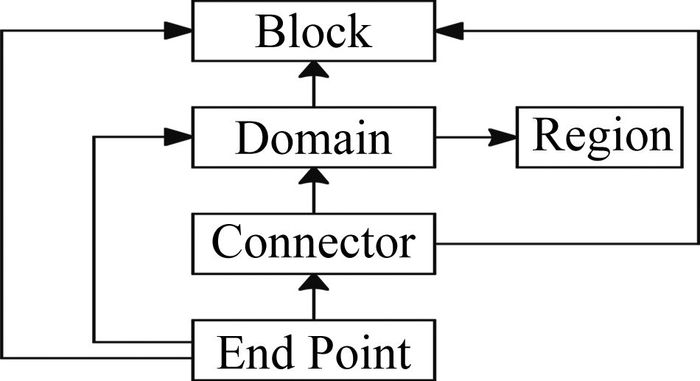
为表述方便,将网格中的端点、线、面、体依次称为EndPoint、Connector、Domain和Block;同时,将记录网格分区数据关系信息的元素称为Region。当通过网格框架来生成网格时,不仅要确定离散网格的空间位置以及各网格单元间的相对位置关系,还需要理清网格元素间的关联信息。图 1展示各元素间的依赖关系(由带箭头的连接线表示)。可以看出,各元素间的依赖关系非常复杂,具有较强的数据耦合性。例如,Domain依赖于Endpoint和Connector两个元素,而同时被Block和Region依赖,即存在多对多数据依赖关系。
|
图 1 基础网格数据元素依赖关系 Figure 1 Dependence among various grid data elements |
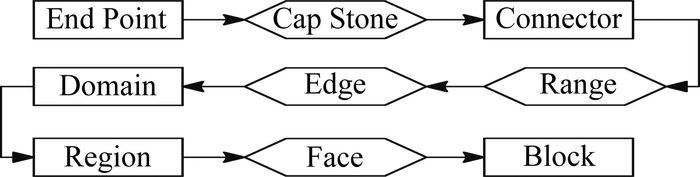
为清晰地表达网格数据关系,在基本网格元素之间增加4个过渡数据层,从而网格数据元素间的依赖关系变为图 2所示的单向串联模式,即将网格中关系复杂、耦合强烈的多对多数据关系分解为若干个多对一或一对一数据关系。尽管此时仍然存在数据耦合现象,但这些数据关系均是单向关联的。例如,一个End Point可能关联多个Cap Stone,但Cap Stone与Connector则是一对一关系。
|
图 2 加过渡元素后的依赖关系 Figure 2 Dependence after adding transition elements |
除上述数据结构和数据间关联关系外,网格框架还记录网格生成相关的辅助信息,如网格面的投影关系、网格线离散的分布函数、单一网格块生成的算法等。这些信息涉及网格生成的具体方法,但是与网格框架变形过程无关。
1.3 网格框架提取采用多块对接结构网格进行CFD计算时,需要输入的网格信息包括网格点几何坐标、网格块对接关系以及边界条件等。其中,对接关系信息处理是提取网格框架的关键环节。
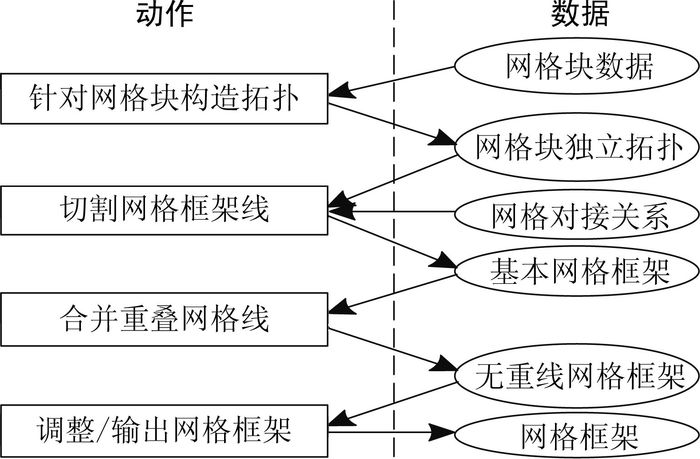
网格框架的提取流程如图 3所示,主要包含如下步骤:
|
图 3 网格框架提取流程 Figure 3 Extraction flow of grid framework |
1) 构造网格块拓扑。对每个网格块,利用对应块数据中的8个顶点和12条棱信息来构造网格框架。需要注意的是,组成网格框架的这些点/线可能是相互交错的,即一条网格线与另一条网格线可能部分或全部对应。
2) 切割网格框架线。根据网格对接关系信息,提取出网格框架线之间的错位点和重叠程度等信息,进而将较长的网格线拆分成较小且无错位的网格线。此时网格框架已基本成型,但块对接处的网格线是重复的。
3) 合并重叠网格线。鉴于重复网格线中网格点的几何坐标相同,利用网格点坐标进行重叠判断并剔除重复信息,得到无重叠网格线的网格框架。
4) 调整/输出网格框架。调整网格线、网格面和网格块的组装关系,得到完整的网格框架。
2 网格自动重构技术在优化、气动弹性等多学科耦合计算过程中,外形通常在某些特定区域(如优化设计点、机翼梢部等)存在较大的变形。对于这些变形带来的局部位移,最终将沿着图 2所示的顺序逐步传递到整个网格。
2.1 网格框架变形技术在此采用样条曲线拟合技术实现网格框架的变形处理。其基本思路是:首先寻找同时满足如下条件的样条曲线,即在壁面或近物面处保持网格框架线与物面正交,而在空间上尽量贴近原始网格中的相应网格线;然后用得到的样条曲线代替原网格框架中的网格线。该方法得到的样条曲线能够较好地适应物面变形、最大限度地保持壁面网格正交性并提供直观的边界控制方法。
假设拟合曲线的三次参数方程为
| $\left\{ {\begin{array}{*{20}{l}} {x\left( t \right) = {a_x}{t^3} + {b_x}{t^2} + {c_x}t + {d_x}}\\ {y\left( t \right) = {a_y}{t^3} + {b_y}{t^2} + {c_y}t + {d_y}}\\ {z\left( t \right) = {a_z}{t^3} + {b_z}{t^2} + {c_z}t + {d_z}} \end{array}} \right.$ | (1) |
其中t∈(0, 1),a、b、c和d是系数。通过网格线的端点P0、P1以及端点的方向向量,可以得到计算拟合曲线系数的方程组
| $\left\{ {\begin{array}{*{20}{l}} {{d_x} = {P_{0x}}}\\ {{c_x} = d{P_{0x}}}\\ {{a_x} + {b_x} + {c_x} + {d_x} = {P_{1x}}}\\ {3{a_x} + 2{b_x} + {c_x} = d{P_{1x}}} \end{array}} \right.$ | (2) |
求解上述方程组即可得到拟合曲线的解析表达式。当然,仅仅通过一次简单计算所得到的曲线只在端点上与原网格框架线重合,并不能保证拟合曲线与原网格框架线在空间上的一致性。为此,可以寻找拟合曲线的最大误差点并在该点处插入新节点,然后重复上述曲线拟合过程,直至拟合曲线的最大误差小于给定值。该过程一般会在初次拟合曲线中插入3至4个中间节点。
拟合的框架线是实现网格框架变形处理的有力工具。一方面,变形动作仅在框架线的节点上而非整个框架线上进行,可较好地避免网格复杂、网格变形量大等情况下网格框架线变形失败的情况。另一方面,拟合曲线的物理意义较直观且操控方便,在变形中可通过强制曲线物面端方向导数保持不变或与物面正交来保证附面层内网格的性质;同时,通过放松对远端节点的控制(使其变成自由端点)来均衡复杂变形问题带来的冲突性变形要求,可以大大提升网格框架线在物面变形时的适应能力。
2.2 网格重构从原始网格提取出的网格框架线包含了原网格拓扑的完整信息,因此在网格框架变形中只要其拓扑结构保持不变,就可以利用该网格框架还原出变形后满足计算需求的新网格。
在网格框架中,仅删除了网格面、网格块对象中不适应变形的网格点几何数据,而它们之间的关联关系(如网格面由哪些网格线组成、网格块由哪些网格面组成等信息)被完整保留,即可以据此顺利完成网格重构工作。
网格重构过程中采用较鲁棒的超限插值(TransFinite Interpolation,TFI)方法,并在用户关心的附面层等特定区域上借助曲率修正网格方法来进行壁面正交性优化,以保证生成网格的质量。在特殊条件下,为保证网格生成的质量,也可以在局部应用一些偏微分方程方法。
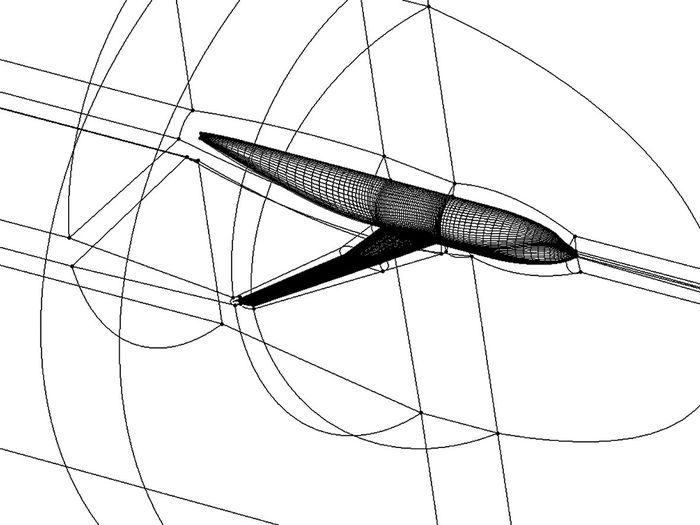
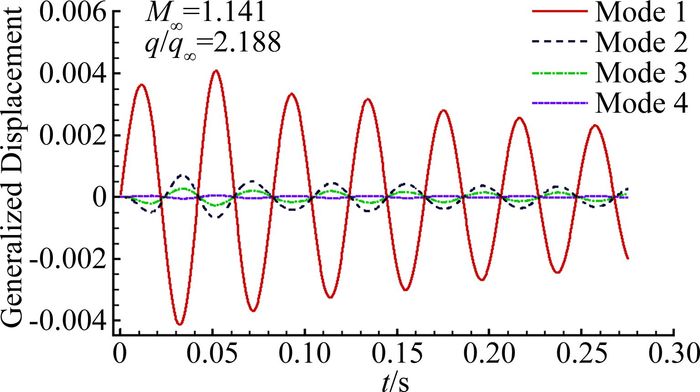
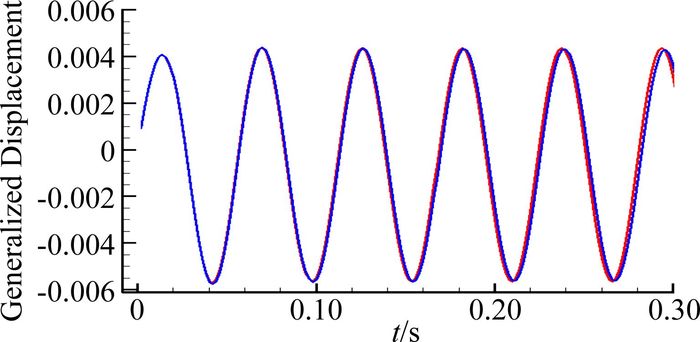
3 算例验证图 4至图 7显示网格重构方法在相对复杂的翼身组合体气动弹性计算中的应用情况。图 4显示计算所用外形的表面网格以及网格框架线。该方法对附面层区域框架线进行了特化处理,使其保持刚体运动,保证了当变形大于附面层区域时依然可以完成网格重构。图 5展示不同模态的广义位移响应曲线。由于采用了上述高精度结构对接网格重构方法,流体计算可以在较精细的网格上进行,从而解决了传统方法处理时网格较粗糙、无法满足流体粘性计算对高精度附面层网格的需求,提升了气动弹性耦合计算的整体精度。图 6展现出Euler及N-S方程计算得到的广义位移响应曲线差异,可以看到两者的差异随时间的推移由细微逐渐变得明显,流体的粘性效应对计算结果产生了显著影响。
|
图 4 翼身表面网格与网格框架 Figure 4 Wing-body surface grid and framework |
|
图 5 不同模态的颤振特性 Figure 5 Flutter features at different modes |
|
图 6 Euler及N-S方程计算得到的广义位移差异 Figure 6 Difference between generalized displacement obtained with Euler and N-S equations |
|
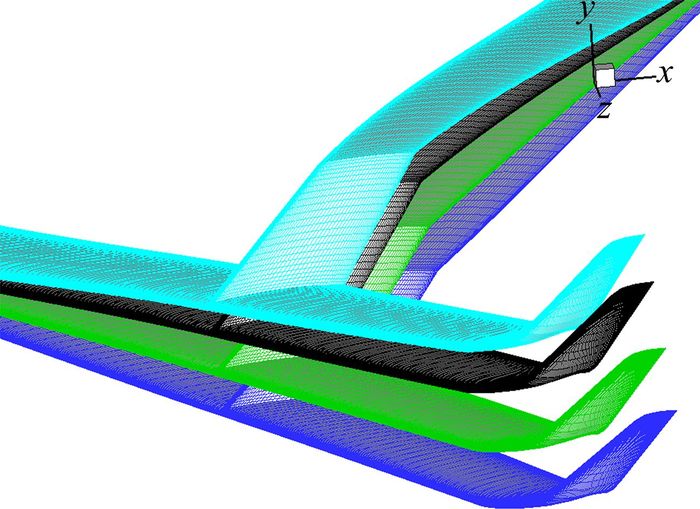
图 7 各计算状态下的机翼变形图 Figure 7 Wing deformation corresponding to various angles of attack |
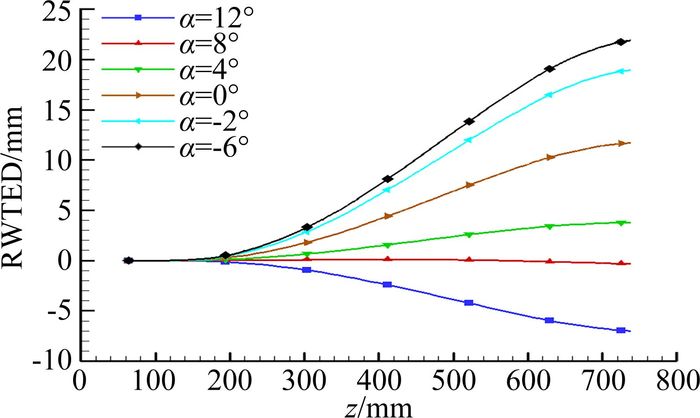
为进一步验证该方法的适用性,将其应用于某“Φ”型联接翼飞行器的机翼气动弹性性能评估中。根据工程经验,机身对静气动弹性修正的影响非常有限,因此静气动弹性分析重点考虑联接翼部分,其外形及气动弹性变化情况如图 7所示。该联接翼飞行器的飞行高度为10km、巡航马赫数为0.8。较长的翼展造成该飞行器的机翼变形较大,而联接翼处网格结构非常复杂,致使传统的网格弹性变形法无法有效处理此处的变网格问题。图 8是飞行器的部分计算结果。从静气动弹性计算结果可以看出,挠度随马赫数和攻角单调递增;另外,在计算过程中也发现,如果去掉前后翼中间的连接部分,后掠翼的挠度将变得很大,而前掠翼则相对变化不大。由于连接部分的存在,后掠翼的弹性变形受到抑制,最终使得整体的气动特性维持在比较满意的水平。
|
图 8 前后翼挠度变化趋势 Figure 8 Spanwise distributions for deflection of front-wing and rear-wing |
本文提供了一个可行的结构网格自适应重构方法,能够自适应物面大尺度变形问题,处理过程自动快捷且与CFD解算器无关。通过一定的附面层网格处理技巧,处理能满足气动弹性、多学科优化设计等基于CFD的多学科耦合计算领域对网格变形的要求,有利于提高CFD计算精度。通过人机交互方式指定特殊区域在网格自动变形中的处理方式,可增加方法的健壮性,拓展方法的应用范围。
复杂外形的附面层网格处理是目前方法遇到的最大障碍,也是未来工作的重点。在下一步工作中,将尝试类似于网格框架线提取的过程,利用原始网格信息,通过变形后的表面网格重构附面层网格框架线,而不是对原网格附面层框架线变形来得到新网格。同时,尝试将该方法集成到多块分区并行软件PMB3D的前置处理模块,提高其对大变形问题的适应能力。
| [1] |
龚军锋, 祝小平, 周洲. 基于结构动网格的无人机地面效应研究[J]. 航空工程进展, 2012, 3(3): 263-269. (  0) 0) |
| [2] |
洪俊武, 王运涛, 庞宇飞, 等. 结构网格方法对高升力构型的应用研究[J]. 空气动力学学报, 2012, 31(1): 75-81. (  0) 0) |
| [3] |
王运涛, 王光学, 徐庆新, 等. 基于结构网格的大规模并行计算研究[J]. 计算机工程与科学, 2012, 34(8): 63-68. (  0) 0) |
| [4] |
周培培. 基于结构网格的栅格翼绕流数值模拟[J]. 空气动力学学报, 2014, 32(3): 334-338. (  0) 0) |
| [5] |
朱君, 赵宁. 结构网格MWENO-7格式的构造和应用[J]. 南京航空航天大学学报, 2007, 39(4): 440-443. (  0) 0) |
| [6] |
孙俊峰, 刘刚, 江雄, 等. 基于Kriging模型的旋翼翼型优化设计研究[J]. 空气动力学学报, 2013, 31(4): 437-441. (  0) 0) |
| [7] |
王俊毅, 招启军, 肖宇. 基于CFD/CSD耦合方法的新型桨尖旋翼气动弹性载荷计算[J]. 航空学报, 2014, 35(9): 2426-2437. (  0) 0) |
| [8] |
詹浩, 程诗信, 朱军. 考虑气动弹性影响的机翼复杂气动外形设计研究[J]. 西北工业大学学报, 2009, 27(2): 100-104. (  0) 0) |
| [9] |
倪同兵, 招启军, 赵国庆, 等. 应用多块对接结构网格方法的直升机涵道尾桨气动特性分析[J]. 空气动力学学报, 2011, 29(6): 688-696. (  0) 0) |
| [10] |
Gaitonde A L, Fiddes S P. A moving mesh system for the calculation of unsteady flows[R]. AIAA 1993-0641, 1993.
(  0) 0) |
| [11] |
Banita J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes[J]. AIAA Journal, 1990, 28(8): 1381-1388. DOI:10.2514/3.25229 (  0) 0) |
| [12] |
Tezduyar T E. Stabilized finite element formulations for incompressible flow computations[J]. Advances in Applied Mechanics, 1992, 28(1): 1-44. (  0) 0) |
| [13] |
Heathcote S, Martin D, Gursul I. Flexible flapping airfoil propulsion at zero freestream velocity[J]. AIAA Journal, 2004, 42(11): 2196-2204. DOI:10.2514/1.5299 (  0) 0) |
| [14] |
周璇, 李水乡, 孙树立, 等. 非结构网格变形方法研究进展[J]. 力学进展, 2011, 41(5): 547-561. DOI:10.6052/1000-0992-2011-5-lxjzJ2011-050 (  0) 0) |
| [15] |
Shyy W, Aono H, Chimakurthi S K. Recent progress in flapping wing aerodynamics and aeroelasticity[J]. Progress in Aerospace Sciences, 2010, 46(7): 284-327. DOI:10.1016/j.paerosci.2010.01.001 (  0) 0) |
| [16] |
Sudhakar Y, Vengadesan S. Flight force production by flapping insect wings in inclined stroke plane kinematics[J]. Computers & Fluids, 2010, 39: 683-695. (  0) 0) |
| [17] |
Liu X Q, Qin N, Xia H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423. DOI:10.1016/j.jcp.2005.05.025 (  0) 0) |
| [18] |
Boer A, Schoot M S, Faculty H B. Mesh deformation based on radial basis function interpolation[J]. Computers and Structures, 2007, 85(11): 784-795. (  0) 0) |
| [19] |
张伟伟, 高传强, 叶正寅. 气动弹性计算中网格变形方法研究进展[J]. 航空学报, 2014, 35(2): 303-319. (  0) 0) |
| [20] |
张来平, 段旭鹏, 常兴华, 等. 基于Delaunay背景网格插值和局部网格重构的变形体动态混合网格生成技术[J]. 空气动力学学报, 2009, 27(1): 32-40. (  0) 0) |
| [21] |
郑赟, 王彪, 王静, 等. 多块协调变形的网格变形技术及其应用[J]. 航空计算技术, 2012, 42(1): 83-87. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


