高超声速轴对称风洞喷管设计中(特别是出口Ma>10的喷管),有时会存在风洞实际流场与设计流场不一致的问题。差异产生的原因最大可能来源是喷管的无黏型面设计。无黏型面设计分收缩段和扩张段两部分。扩张段常用较为严格的气动特征线方法设计,而收缩段常用光滑的数学函数构造,而非由气动理论严格导出[1]。要研究喷管无黏型面设计是否理想,首先应开展收缩段设计研究。
收缩段的作用是提高试验段流场品质、降低试验段湍流度、提高速度均匀性和稳定性。因此要求气流在收缩段内不能发生分离,在出口处流场具有较好的速度均匀性、较低的湍流度[2-5]。从公开发表的文献看,收缩段设计关于高超声速喷管方面的研究相对较少,更多文献集中在研究低速风洞、水洞等低速不可压缩流动相关的设备上。尽管在很多超声速喷管设计实践中也应用与低速喷管同类型的收缩曲线,但需要注意,在超声速喷管设计中应用的喉部声速线通常是弯曲的,而不是均匀直线。
收缩段的主要设计参数为收缩段长度、收缩比和收缩曲线类型。长度和收缩比的选择需要综合考虑流场品质问题(如均匀性和避免分离等)和经济问题[5]。收缩曲线常用类型包括:双三次曲线[6]、移轴或不移轴的维托辛斯基(简称维氏)曲线[5]、巴切勒曲线[7]、五次曲线[5]、优化的双三次曲线[8]、优化的五次曲线[9]、五次加锥形加五次(QCQ)分段曲线[10]等。收缩曲线类型根据试验设备的流动要求进行选择,往往因试验设备和目标应用的不同而变化。国内学者根据不同要求开展低速流动设备的喷管收缩段曲线类型研究[9-15],表明在不同的应用中各曲线类型互有优劣。对于超声速喷管的收缩段设计,易仕和等[5]根据经验提出了喉部型面曲率半径应该小于收缩段入口曲率半径等注意点。AEDC的超声速喷管收缩段设计实践中也总结了7条设计规则。Shope等人为了研究这7条规则是否完全必要,分析了基于sin函数、椭圆曲线构造的收缩段对于超声速喷管出口流场的影响,与采用QCQ分段曲线的基准状态进行了比较[1]。结果表明当几何喉道处曲率半径连续时,收缩段上游的转折角变化、曲线曲率连续与否对喷管扩张段出口的流动均匀性影响不明显,而几何喉道处曲率半径不连续则显著影响喷管出口的流动。
在Shope的研究中仅考虑了几何喉道上游(收缩段出口)曲率半径小于喉道下游(扩张段入口)曲率半径时的喉道曲率不连续,而没有考虑大于的情况。且因为构造的曲线曲率半径是连续变化的,与喉道跨声速近似解的曲率半径是固定值的假设不同,其中差异也需要进一步研究。收缩段设计直接影响喉部跨声速解,也必将影响需利用喉部跨声速解的扩张段设计。因此研究喷管收缩段设计还需要同时研究其对喉部跨声速流动和不同方法设计的扩张段流动的影响。
1 喉道上游固定曲率收缩段为研究喉道上游曲率半径对于喉部跨声速流动和喷管扩张段流动的影响考虑构造AQA分段曲线。该曲线由圆弧加五次曲线加圆弧构成,因而在收缩段出入口具有固定的曲率半径,这与Kliegel等喉道跨声速近似解的假设一致。
AQA分段曲线表达式为:
| $ \begin{array}{l} {\left( {x - {x_{01}}} \right)^2} + {\left( {y - {y_{01}}} \right)^2} = \rho _u^2\\ y = {c_0} + {c_1}x + {c_2}{x^2} + {c_3}{x^3} + {c_4}{x^4} + {c_5}{x^5}\\ {\left( {x - {x_{02}}} \right)^2} + {\left( {y - {y_{02}}} \right)^2} = \rho _u^2 \end{array} $ | (1) |
其中:两条圆弧的半径取喉道上游的曲率半径ρu,圆弧对应的角度取θ, (x01=-L, y01=ri-ρu)为入口处圆弧圆心,(x02=0, y02=rt+ρu)为出口处圆弧圆心,L为收缩段长度,ri为收缩段入口半径,rt为收缩段出口半径(即几何喉道半径),五次曲线的系数c0~5根据在两个端点处y坐标值、一阶导数、二阶导数相等共6个条件确定。
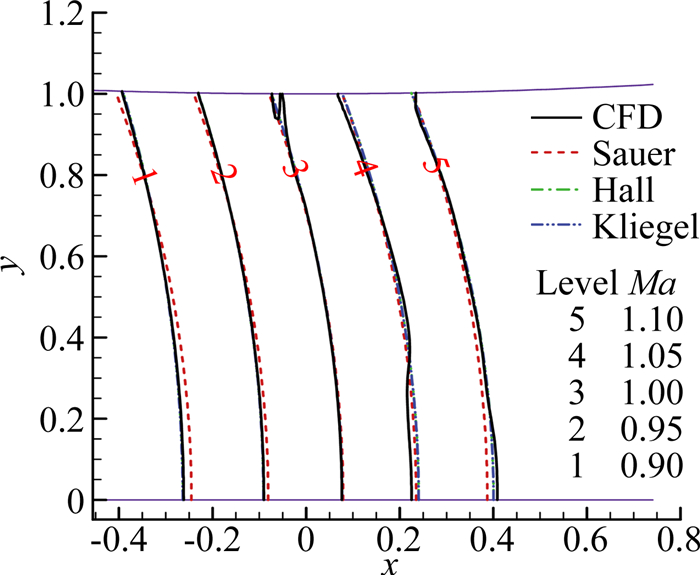
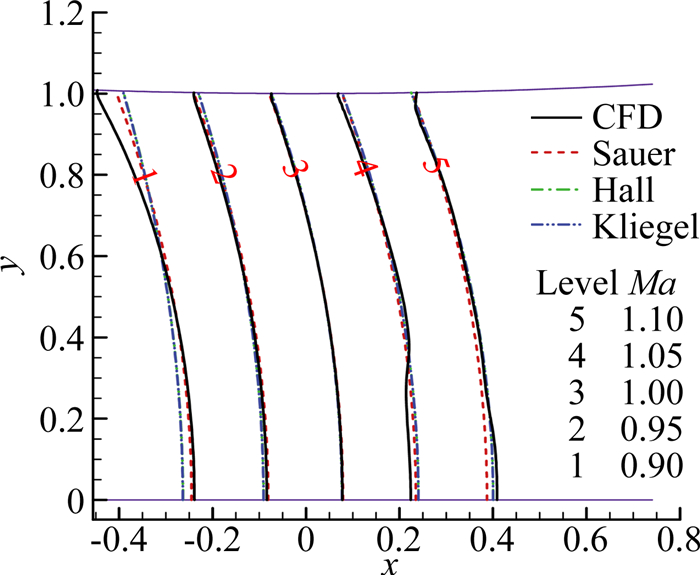
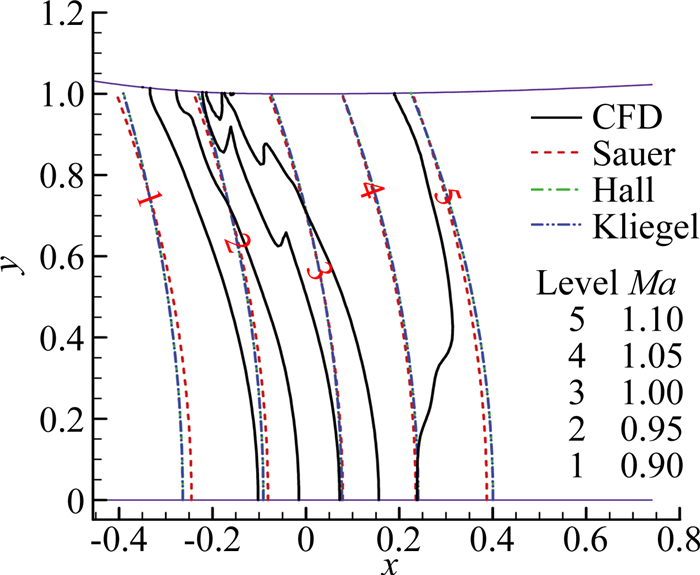
1.1 喉道曲率连续时圆弧长度对喉部流场的影响利用喉道上下游均采用圆弧(曲率固定)来考察喉道曲率半径连续(ρu=ρd)时的问题,其中ρd为喉道下游圆弧的曲率半径,取喉道曲率半径比ρd/rt=12进行考察。取喉道上游圆弧段对应的角度为θ=5.73°、2.865°、0.573°时,利用数值模拟得到喉道马赫数等值线与采用跨声速近似解方法(分别计算Sauer、Hall、Kliegel三种方法)得到的喉部马赫数等值线比较如图 1~图 3所示。θ=0.573°时,4种方法的声速线基本一致,往上游移动,Sauer方法的结果偏差变大,而Hall和Kliegel方法的结果与CFD结果基本一致(图 1)。当θ=2.865°时,声速线也基本一致,在喉道上游近似方法结果与CFD结果均存在偏差(图 2)。而当θ=0.573°时,近似解与CFD结果已无法比较,说明喉道上游的圆弧已经短得无法产生与近似解相近的流动(图 3)。上述结果表明:当喉道上下游曲率半径相等时(喉道曲率半径连续),喉道上游的圆弧段需要有足够角度(即足够长度)才能确保喉部区域流动与喉部跨声速近似解接近。因而当扩张段设计需要利用喉部跨声速近似解时,不仅需要喉道曲率半径连续,还需要在喉道上游一定长度内保证该曲率半径,若曲率半径变化太快,即便在喉道处曲率连续,也可能出现问题。
|
图 1 圆弧θ=5.73°时喉部马赫数等值线 Figure 1 Mach contours at throat for θ=5.73° |
|
图 2 圆弧θ=2.865°时喉部马赫数等值线 Figure 2 Mach contours at throat for θ=2.865° |
|
图 3 圆弧θ=0.573°时喉部马赫数等值线 Figure 3 Mach contours at throat for θ=0.573° |
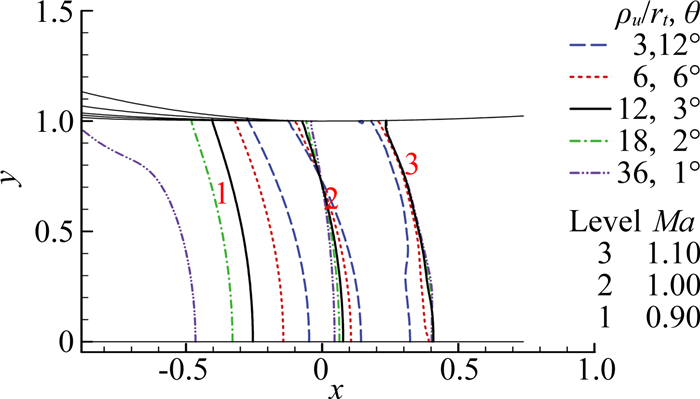
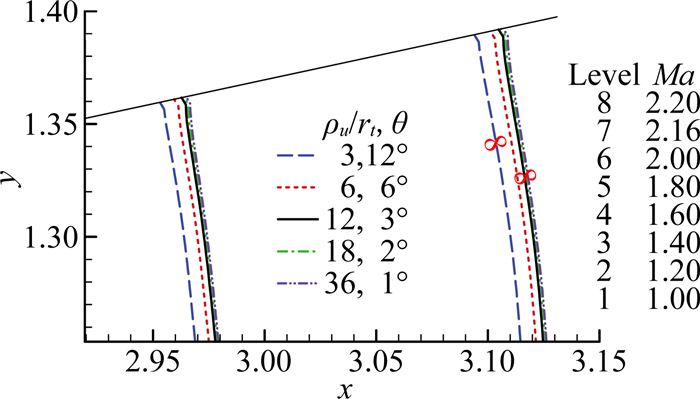
为研究喉道处曲率半径不连续的影响,对如下状态进行比较(扩张段固定,喉道下游曲率半径比取ρd/rt=12),ρu/rt分别取3、6、12、18、36和12, θ取6°、3°、2°、1°,各状态的弧长相等。不同状态的喉部和下游某处靠近壁面的马赫数等值线如图 4、图 5所示。当收缩段出口(喉道上游)圆弧曲率半径增大,则声速点往前移动,反之则后移。喉道上游曲率半径比为3、6、18、36的结果与曲率半径为12的结果在喉道上游区域差别均较大,而在下游区域曲率半径比为3、6结果的明显比曲率半径比为18、36的偏差大(图 4)。
|
图 4 喉道曲率半径不连续时喉部马赫数等值线 Figure 4 Mach contours at throat with discontinuous throat |
|
图 5 喉道曲率半径不连续时扩张段下游某处马赫数分布 Figure 5 Mach contours in the expansion section with discontinuous throat |
从扩张段的马赫数等值线比较看,曲率半径比为3、6的结果比曲率半径比为18、36的偏差大,且曲率半径比为3和36的结果分别比曲率半径比为6和18的偏差大(图 5)。上述结果表明:喉道曲率半径连续性越差导致偏差越大,且喉道上游曲率半径小于下游曲率半径的结果比之大于的情况明显偏差大,说明上游曲率半径偏小比偏大对流场的影响更明显。
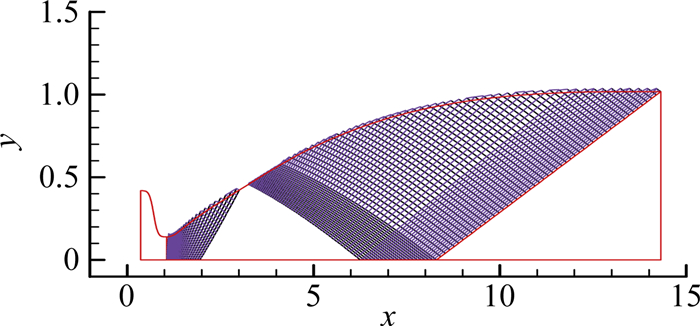
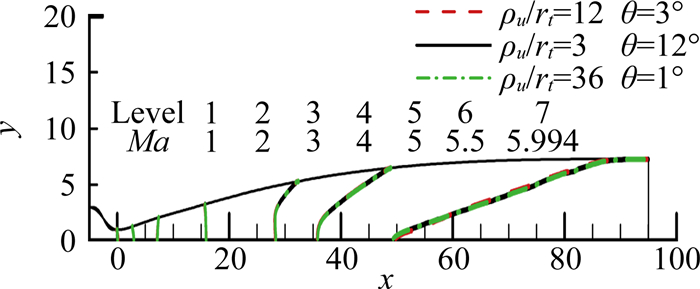
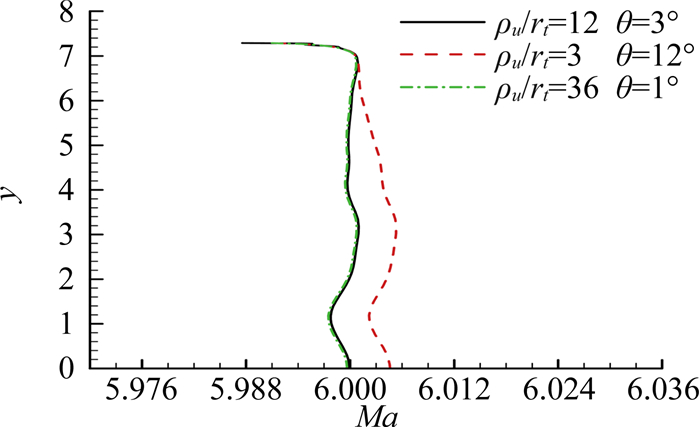
1.3 喉道曲率不连续对于Sivells喷管流场的影响采用Sivells方法设计了Ma=6的无粘喷管扩张段,喉道下游曲率半径比ρd/rt=12,转折角ω=8°,特征线计算过程中取泉流半径为1(图 6为特征线网),完成型面后放大到喉道半径rt=1。设计了三条AQA分段曲线的收缩段进行比较,收缩段出口曲率半径ρu分别为3、12、36,数值模拟考虑总温600K,总压1MPa。图 7所示的喷管内马赫数等值线表明当喉道曲率半径不连续时,在不放大细节的情况下,看不出明显差别。而图 8给出了喷管出口马赫数比较,表明上游曲率半径为12(即喉道曲率半径连续)时,喷管出口除了上壁面附近区域马赫数与设计马赫数偏差达到最大0.2%外,其它区域偏差小于0.05%。当喉道上游曲率半径为36时,马赫数偏差比曲率半径为12时略大但很接近。而当喉道上游曲率半径为3时,马赫数偏差增大,除上壁面附近区域外马赫数偏差从0.05%增大到0.1%。表明喉道曲率半径不连续性使得喷管实际无粘流场(利用数值模拟结果替代分析)与设计流场偏差变大,而且喉道上游曲率半径偏小比偏大影响更显著。
|
图 6 Sivells方法扩张段设计过程中的特征线网 Figure 6 Chracteristic network of Sivells nozzle |
|
图 7 Ma=6喷管马赫数等值线 Figure 7 Mach contours of Ma=6 nozzle |
|
图 8 Ma=6喷管出口马赫数分布 Figure 8 Mach number at exit of Ma=6 nozzle |
一些常用曲线如双三次曲线的收缩段出口曲率半径无穷大,所以无法与下游型面曲率连续。而维氏移轴曲线,当收缩段长度和收缩比确定后形状即确定,出入口的曲率半径可以通过移轴调整。移轴量rh增大,则入口曲率半径增大,出口曲率半径减小,但其最大出口曲率半径是确定的。为了方便讨论,本节将构造两种曲率半径变化且任意可调的收缩曲线,分别基于三角函数加双曲函数、B-样条函数[16-17]构造。
2.1 由三角函数和双曲函数构造的曲线曲线表达式为:
| $ \begin{array}{l} f\left( x \right) = {r_t} + \frac{{\left( {{r_i} - {r_t}} \right)}}{2}.\\ \left\{ {\sin \left[{\frac{{\tanh \left( {\left( {a + b} \right)\frac{x}{L}-a} \right) + \tanh \left( a \right)}}{{\tanh \left( b \right) + \tanh \left( a \right)}}{\rm{ \mathsf{ π} }} + \frac{{\rm{ \mathsf{ π} }}}{2}} \right] + 1} \right\} \end{array} $ | (2) |
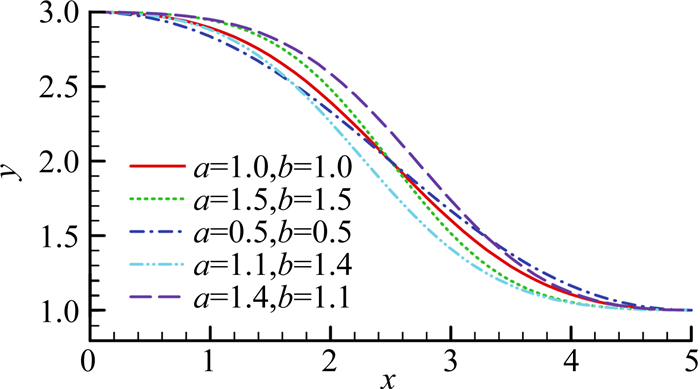
构造思路是利用sin函数使出入口处的斜率为0,利用tanh函数方便地调整曲线收缩的剧烈程度。其中a、b参数可用于调整入口和出口处曲线的形状和曲率半径,增大a可以使入口更平缓,曲率半径增大,增大b则可调整出口。由图 9看,当a=b时,曲线在中点两侧奇对称;当a大于b时,入口处的曲率半径大于出口曲率半径;反之亦然。
|
图 9 sin&tanh曲线L=5rt,ri=3rt Figure 9 Curve constructed by sin and tanh function with L=5rt, ri=3rt |
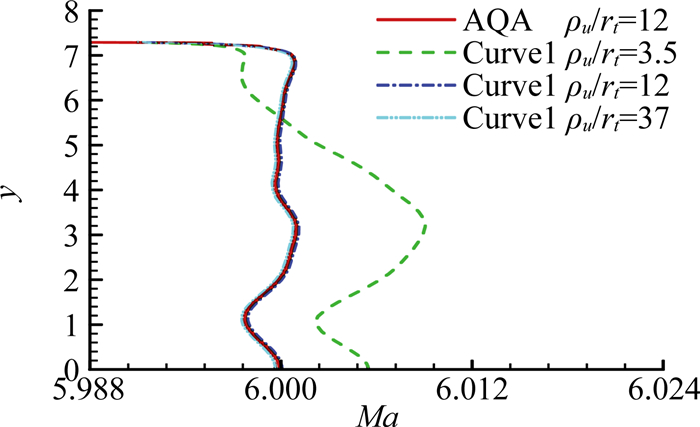
考虑如下不同a、b参数的曲线作为Ma=6喷管收缩段,并与AQA分段曲线的结果进行比较。(1) a=b=0.5, ρu/rt=3.498; (2) a=b=1.162, ρu/rt=12.0; (3) a=b=1.6, ρu/rt=37.09。图 10为喷管出口的马赫数分布。喉道上游曲率半径比为12、37的两个状态与AQA曲线曲率半径比为12的马赫数非常接近,曲率半径比为37的Ma略大,而曲率半径比为12的Ma略小。而曲率半径比为3.5的出口马赫数与AQA曲线结果偏差较大,接近0.2%。注意到,喉道上游曲率半径比为12的状态,其曲率半径是连续变化的,往上游移动曲率半径连续减小,产生的结果为:出口马赫数比AQA曲线变大,但偏差要比喉道曲率不连续(曲率半径比为3.5)的状态小。可见曲率半径连续变化且在喉道处曲率连续的曲线,相当于其平均曲率半径比略小于固定曲率半径连续时的情况。当喉道曲率半径不连续时,喉道上游的曲率半径偏小则喷管出口靠近轴线区域马赫数相比喉道曲率半径连续时偏大,反之亦然。且当喉道上游曲率半径偏小时,马赫数偏差明显大于喉道上游曲率偏大时的情况。
|
图 10 sin&tanh函数曲线收缩段喷管出口马赫数分布 Figure 10 Mach number at exit of the nozzle with contraction constructed by sin&tanh function |
P次B样条曲线定义为:
| $ \begin{array}{l} f\left( u \right) = \sum\limits_{i = 0}^n {{N_{i, p}}\left( u \right)} {P_i}, a \le u \le b\\ {N_{i, 0}}\left( u \right) = \left\{ \begin{array}{l} 1, \;\;\;\;\;{u_i} \le u \le {u_{i + 1}}\\ 0, \;\;\;\;\;{\rm{otherwise}} \end{array} \right.\\ {N_{i, p}}\left( u \right) = \frac{{u - {u_i}}}{{{u_{i + p}} - {u_i}}}{N_{i, p - 1}}\left( u \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{u_{i + p + 1}} - u}}{{{u_{i + p + 1}} - {u_{i + 1}}}}{N_{i + 1, p - 1}}\left( u \right) \end{array} $ | (3) |
其中:Pi(i=0, n)为n+1个控制点,需要利用对应数量的p阶基函数Ni, p(u)构成p次曲线,而n+1个基函数相应的需要m+1 (m=n+p+1)个节点构造。B-样条曲线是u(u∈[0, 1])的函数,对于平面上的曲线,控制点Pi(i=0, n)为(x, y)坐标,相当于式(3)需要对x、y各计算一遍,因此B-样条曲线为参数方程表示的曲线,其曲率半径计算式为:
| $ \begin{array}{l} x\left( u \right) = \varphi \left( u \right)\\ y\left( u \right) = \psi \left( u \right)\\ \rho \left( u \right) = \frac{{{{\left[{{{\varphi '}^2}\left( u \right) + {{\psi '}^2}\left( u \right)} \right]}^{\frac{3}{2}}}}}{{\left| {\varphi '\left( u \right)\psi ''\left( u \right) - \varphi ''\left( u \right)\psi '\left( u \right)} \right|}} \end{array} $ | (4) |
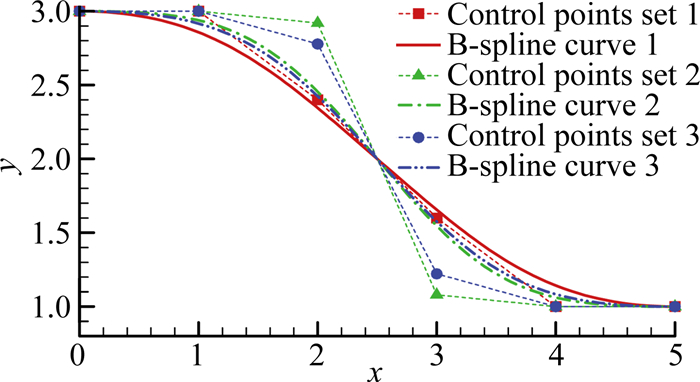
基于B-样条曲线设计的收缩段出入口的曲率半径和曲线的形状可以通过调整控制点改变。为保证出入口的斜率为0,首端和尾端的前两个控制点y坐标值应设为相同,曲率半径通过第三及以后的点来调整。考虑利用如下不同控制点的4次B-样条曲线(图 11)构造Ma=6喷管收缩段,并与AQA曲线的结果进行比较。
|
图 11 不同控制点的4次B-样条曲线 Figure 11 B-spline curve of with different control points |
1) x=[0, 0.2L, 0.4L, 0.6L, 0.8L, L],y=[ri, ri, ri-0.08rt, rt+0.08rt, rt, r];
2) x=[0, 0.2L, 0.4L, 0.6L, 0.8L, L],y=[ri, ri, ri-0.22222rt, rt+0.22222rt, rt, rt];
3) x=[0, 0.2L, 0.4L, 0.6L, 0.8L, L],y=[ri, ri, ri-0.6rt, rt+0.6rt, rt, rt]。
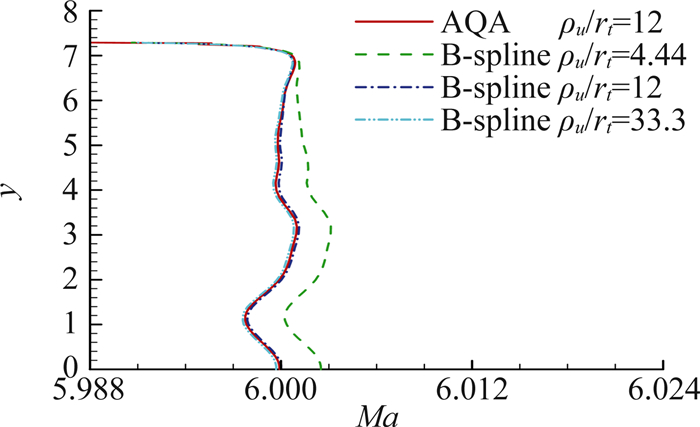
3条曲线的喉道上游曲率半径比为:4.4、12、33.3。B-样条曲线的结果(图 12)与上一小节构造曲线的结果类似,B-样条曲线喉道上游曲率半径比4.4的结果比之上一小节曲率半径比3.5的结果偏差要小。从两个小节的结果可以得出:当喉道曲率半径连续时,喷管无粘流场与设计状态更为接近。而当曲率半径不连续时,对于同一个扩张段,喉道上游曲率半径偏小,则喷管轴线附近流动的膨胀程度偏高。而当上游曲率半径偏大,则膨胀程度偏低,但与曲率半径连续时的情况很接近。
|
图 12 B-样条曲线收缩段喷管出口马赫数分布 Figure 12 Mach number at exit of the nozzle with B-spline curve contraction |
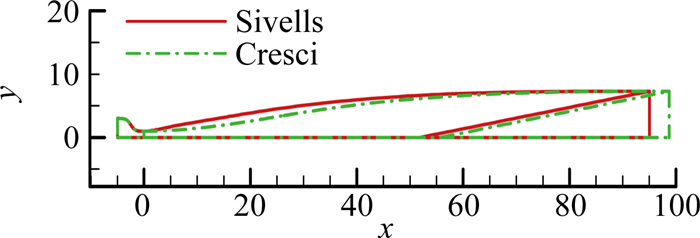
扩张段采用Cresci方法设计以考察收缩段对不基于喉道跨声速解设计的喷管的影响。因为喉道与泉流上壁面终点之间的曲线为3次曲线,喉道下游曲率半径比采用相等转折角的Sivells喷管大(图 13)。取设计参数:出口马赫数为6,轴线上泉流终点马赫数为5.8,转折角为8°。喉道下游曲率半径比为93.74。收缩段采用2.1小节构造的曲线。考虑计算3条收缩曲线,a=b为0.5、1.7、1.9233,ρu/rt为3.498、49.07、97.78。
|
图 13 Cresci和Sivells方法喷管型面比较 Figure 13 Comparison between Cresci and Sivells nozzles |
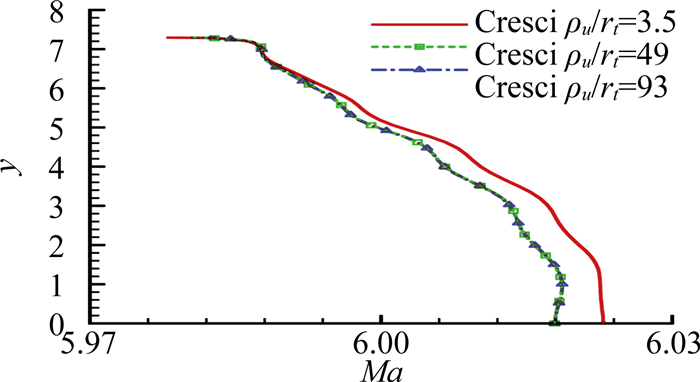
图 14给出了上述3条收缩曲线的Cresci喷管出口马赫数分布。其中喉道上游曲率半径比为3.5的状态喷管出口流动偏离设计状态最显著,马赫偏差接近0.4%。而随着喉道上游曲率半径增大,曲率半径比为49和93的结果基本一致,其马赫数最大偏差接近0.3%。分析喉道上游曲率半径的影响表明:喉道上游曲率半径越偏小,喷管出口的流场与设计状态偏离越大;而当喉道上游曲率半径增大,流场偏离减小;当曲率半径增大到一定程度后,曲率半径对喷管出口流场影响变小。说明对于不基于喉部跨声速解的喷管扩张段设计方法,喉道曲率半径不连续时,喉道上游曲率越偏小同样使得喷管出口流场与设计状态偏差越大。
|
图 14 Cresci喷管出口马赫数分布 Figure 14 Mach number at exit of the Cresci nozzle |
对于高超声速喷管设计,喷管出口流动的均匀性是衡量设计优劣的最终指标。本文的研究表明,收缩段设计对喷管出口流场品质影响明显。当综合考虑选择合适的收缩段长度和收缩比后,构造合适的收缩曲线以保证几何喉道处曲率半径连续是保证喷管实际无粘流场与设计相一致的关键。当无法保证喉道曲率半径连续时,应使喉道上游的曲率半径大于喉道下游曲率半径,而不是相反。
收缩曲线的选择和构造可以多样,可选择分段曲线(如QCQ、AQA曲线),也可选择单函数描述的曲线(如本文构造的基于sin加tanh函数、B样条函数的两种曲线)。重点在于要有适当的参数可使收缩曲线的曲率半径任意可调。调整参数增大收缩段入口的曲率半径,可利于减小边界层厚度和湍流度,调整参数使收缩段出口的曲率半径与喉道下游的曲率半径连续,则利于喷管获得与设计一致的出口流场。
| [1] |
Shope F L, Aboulmouna E A. On the importance of contraction design for supersonic wind tunnel nozzles[C]//26th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 2008. AIAA 2008-3940.
(  0) 0) |
| [2] |
伍荣林, 王振羽. 风洞设计原理[M]. 北京: 北京航空学院出版社, 1985.
(  0) 0) |
| [3] |
姜维本, 罗义成, 狄俊安. 高超声速试验设备设计[M]. 北京: 国防工业出版社, 2001.
(  0) 0) |
| [4] |
刘政崇. 高低速风洞气动与结构设计[M]. 北京: 国防工业出版社, 2003.
(  0) 0) |
| [5] |
易仕和, 赵玉新, 何霖, 等. 超声速和高超声速喷管设计[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [6] |
Morel T. Comprehensive design of axisymmetric wind tunnel contractions[J]. Journal of Fluid Engineering, 1975, 97(2): 225-228. DOI:10.1115/1.3447255 (  0) 0) |
| [7] |
周刚, 汪家道, 陈皓生, 等. 小型高速水洞收缩段的优化设计[J]. 船舶力学, 2009, 13(4): 513-521. (  0) 0) |
| [8] |
张连河, 范洁川. 三元收缩段优化设计研究[J]. 空气动力学学报, 2003, 21(4): 417-423. (  0) 0) |
| [9] |
王帅, 刘小康, 陆龙生. 直流式低速风洞收缩段收缩曲线的仿真分析[J]. 机床与液压, 2012, 40(11): 100-104. DOI:10.3969/j.issn.1001-3881.2012.11.031 (  0) 0) |
| [10] |
Shope F L. Contour design techniques for super/hypersonic wind tunnel nozzles[C]//24th AIAA Applied Aerodynamics Conference, San Francisco, CA, 2006. AIAA-2006-3665.
(  0) 0) |
| [11] |
王喜魁. 风洞高次曲线收缩段壁型及其性能[J]. 空气动力学学报, 1997, 15(2): 251-255. (  0) 0) |
| [12] |
刘卫红. 轴对称收缩段设计研究[J]. 空气动力学学报, 1998, 16(2): 250-254. (  0) 0) |
| [13] |
周勇为, 常熹钰, 易仕和. 低湍流度磁悬浮风洞的气动和结构设计[J]. 流体力学实验与测量, 2001, 15(4): 1-6. (  0) 0) |
| [14] |
李国文, 徐让书. 风洞收缩段曲线气动性能研究[J]. 实验流体力学, 2009, 23(4): 73-76. (  0) 0) |
| [15] |
丛成华, 彭强, 汪伏波, 等. 基于粒子轨迹的结冰风洞收缩段优化设计数值模拟[J]. 航空动力学报, 2012, 27(7): 1555-1561. (  0) 0) |
| [16] |
施法中. 计算机辅助几何设计与非均匀有理B样条(CAGD&NURBS)[M]. 北京: 北京航空航天大学出版社, 1994.
(  0) 0) |
| [17] |
Piegl L, Tiller W. The NURBS book[M]. New York: Springer, 1997.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35

