2. 武汉大学土木建筑工程学院, 湖北 武汉 430072
2. School of Civil and Architectural Engineering, Wuhan University, Wuhan 430072, China
在超高建筑涡致振动过程中,气动弹性力包括气动阻尼项、气动刚度项和气动质量项。从既有研究来看,不论是气动阻尼、气动刚度还是涡振响应评估模型,都受到了研究人员的长期重视,并取得了大量成果[1-4]。从既有结论来看,通常认为气动质量项一般可以忽略,气动刚度对风致响应的影响也很小;并且,当涡脱频率接近结构频率造成锁定现象发生时,涡脱频率会被结构频率所俘获,位移响应表现为大幅简谐振动。但是,当超高层建筑更为轻柔时,其气动刚度能否忽略则值得研究,这是本文内容的一个方面。另一方面,由于共振过程中位移曲线并不是理想的正弦曲线,而是有一定的随机性和间歇性,在共振时结构振动频率与涡脱频率并非是传统认为的锁定与被锁定的关系,对此本文亦进行了初步研究。以期为超高层建筑涡振响应的精确评估提供参考。
1 风洞试验如图 1所示,超高层建筑多自由度气弹模型尺寸为1.3m×0.1m×0.1m。该气弹模型很大程度上参考了文献[5]的制作方法,模型具体制作调试方法见文献[6]。

|
图 1 模型照片 Figure 1 Photos of MDOF model |
表 1为模型各工况自振参数,表 1中频率为模型一阶自振频率,频率缩尺比约为100:1,尺寸缩尺比为1:600。表 1中当量质量和Sc数的计算公式如下:
| $ M = \frac{{\int_0^H {m\left( z \right){\phi ^2}\left( z \right){\rm{d}}z} }}{{\int_0^H {{\phi ^2}\left( z \right){\rm{d}}z} }} $ | (1) |
| $ Sc = \frac{{2M{\xi _s}}}{{{\rho _a}{D^2}}} $ | (2) |
| 表 1 模型自振参数 Table 1 Natural vibration features of MDOF model |
|
|
式中,m(z)为单位高度的模型质量,ϕ(z)为平动振型,H为模型总高, ξs、ρa、D分别为阻尼比、空气密度和模型迎风面尺寸。
试验测试内容为不同风速下的横风向风致位移响应。在对模型测响应的同时,在模型表面布置了一定数量的风压测点(部分测压点位置见图 1)。试验风场类型为均匀流和D类粗糙度流场,其平均风速剖面和湍流度剖面见图 2。

|
图 2 D类风场调试结果 Figure 2 Terrain category D |
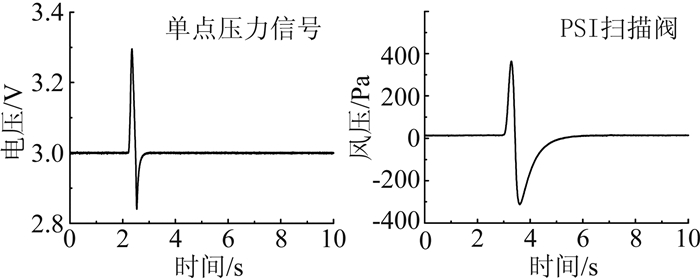
本文设计了一套吹气同步采样系统,来实现风压和位移的同步采集。在气流输入端吹气,经过“三通”分流成两股气流,分别与扫描阀的一个通道和单点压力传感器连接,单点压力传感器与位移计连接在同一个数采板卡上。吹气时两个采样系统有一个通道采集的数据会在同一时刻出现脉冲峰(见图 3)。以此同步时刻为起始点来阶段数据,即实现了风压和位移的同步采集。
|
图 3 同步脉冲信号 Figure 3 Synchronization pulse |
图 4给出了工况1在均匀流场中不同折算风速下的涡振位移响应时程。

|
图 4 共振前后位移响应时程 Figure 4 Displacement time history before and after the VIV |
从图 4来看:a)折算风速较小时,位移时程有很大随机性,其幅值很不稳定。b)随折算风速增大,位移时程接近于简谐;在临界风速附近时,位移时程简谐性最强,但远非理想简谐振动,表现为为“间歇性不稳定共振”。这与既有很多文献尤其是涡振响应评估模型方面的文献结果有很大不同。造成这一现象的原因是,既有研究通常是基于单自由度气弹模型进行的,而单自由度模型相对于多自由度模型的不精确性已被多次证实[6-7]。c)当折算风速继续增大,位移时程又重现出较明显的随机特性,但较之小风速(小于临界风速)下的时程,其振幅则相对稳定。
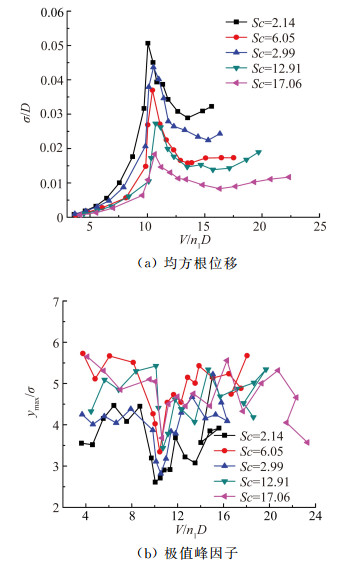
图 5给出了模型在D类流场不同折算风速下的位移响应均方根值σ和极值峰因子。此处的峰因子的含义为响应的最大幅值与均方根值之比,它并不一个严格的概念,只做辅助理解之用。
|
图 5 各工况位移响应(D类流场) Figure 5 Displacement response result(terrain category D) |
从图 5可以看出:在临界风速之前,涡振位移均方根值很小,至临界风速附近迅速增大,而后又有所降低。如果把均方根响应随着算风速的变化曲线看成倒“V”字,那么峰因子就呈现出与之对称的正“V”字,即都在临界风速附近达到极值。事实上,峰因子的大小是涡振位移时程曲线简谐程度的一种度量,理想简谐振动的峰因子为1.414。图 5中峰因子在共振区域近似为2,距离简谐振动还有很大差别。至于共振区域之外的峰因子则明显偏大,在4~5左右,说明此时涡振位移时程的随机性较强。
图 6给出了模型均方根位移随斯科拉顿数(Sc)的变化曲线。从图 6可以看出,各模型均方根位移随Sc的增大而减小;湍流场结果比均匀流场要小,但差别不太大,这是因为D类风场上半部在梯度风高度以上,其流场特性已接近均匀流。就图 6中相对位移的变化趋势来说,本文结果与既有文献的规律是一致的。

|
图 6 不同Sc下共振均方根位移响应 Figure 6 RMS VIV displacement response varying with Sc |
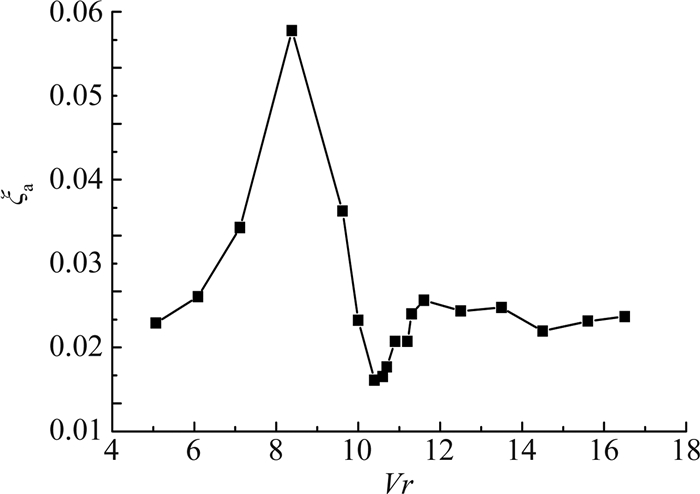
有关气动阻尼ξa的既有文献已经很多,图 7只给出了一条典型变化曲线,此处所用的气动阻尼识别方法为随机减量法。
|
图 7 气动阻尼随折算风速的变化(工况1,均匀流场) Figure 7 Aerodynamic damping varying with Vr (test case 1, uniform flow) |
从图 7可以看出:当折算风速很小时,横风向气动阻尼比约为0,随风速增大而增大;折算风速增大到8附近后,气动阻尼比快速增加,到折算风速达到9到10之间的某个值时,气动阻尼比达到最大正值;随着折算风速的继续增大,气动阻尼比又迅速回落,并在折算风速10.5附近达到最小负值;此后,随着风速的增大,气动阻尼比绝对值迅速回升,而后又大致保持在0附近。上述规律与既有研究结论是一致的。
4 气动刚度分析Vickery[2]等虽然通过定频定幅的强迫振动试验对气动刚(劲)度项进行了分析,由此可结合建筑物密度与流体密度的关系确定出气动刚度造成的频率改变量。Tamura等[8]对于某塔式细柔建筑的频率实测结果也表明,当风致响应较显著时,体系振动频率会偏离其自振频率。但考察气动刚度和气动质量对频率影响的直接方式是气弹模型试验尤其是多自由度气弹模型试验[9],因而用气弹模型直接对频率该变量进行分析是必要而有意义的。
图 8给出了振动模型系统频率n1随折算风速的变化情况。从图 8可以看出,振动系统频率随折算风呈“V”字形变化,在折算风速小于8时,频率改变量为正,当风速接近临界风速时振动频率迅速减小,之后又回升到比自振频率略小的相对稳定的值。从体系频率偏离自振频率的幅度(频率该变量)来看,在共振风速附近的频率改变量与自振频率的比值接近10%,可见涡振对体系频率的影响不可忽略。

|
图 8 体系频率随折算风速的变化 Figure 8 System frequency varying with Vr |
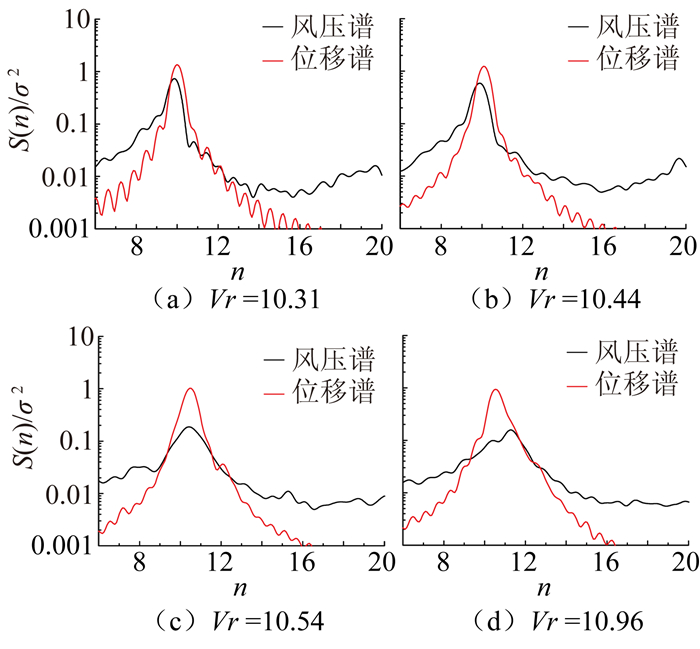
图 9给出了由同步测压得到的风压谱和位移谱,据此可算得共振风速附近风压频率(涡脱频率)与模型振动频率的关系(见图 10)。其中风压数据是在模型中上部两侧全部测点叠加的结果。
|
图 9 风压谱与位移谱对比(工况1,均匀流) Figure 9 Relationship between power spectrum of VIV response and synchronous pressure (case1, uniform flow) |
|
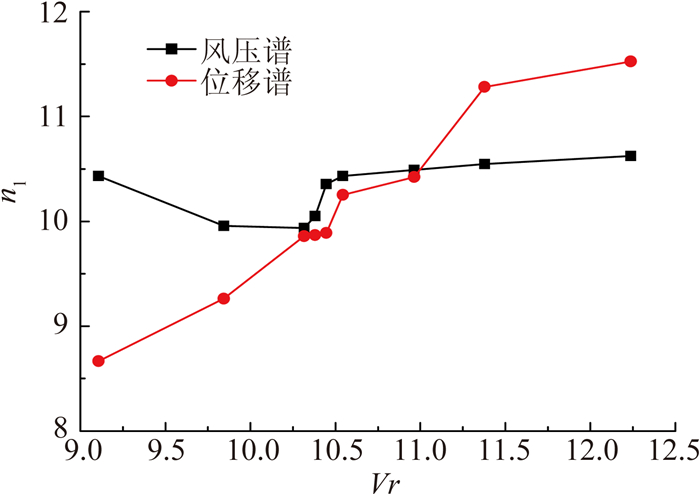
图 10 体系频率与风压频率的关系(均匀流) Figure 10 Relationship between system frequency and vortex frequency (case1, uniform flow) |
从图 10可以看出:a)在折算风速小于临界风速时,风压频率与位移频率差别很大,说明此时不存在共振锁定现象。b)而当折算风速增大到某个值后,模型振动频率与涡脱频率突然变得十分接近;且此时的体系振动频率受涡脱频率影响有显著降低,涡脱频率则受体系振动频率的影响比名义涡脱频率要大;此后的一段折算风速内(Vr=10.3~11.0),涡脱频率十分接近且略小于体系振动频率;随折算风速的增大(或者说随着由来流风速和St数决定的名义涡脱频率的增大),涡脱频率和体系频率都在逐渐增加。c)当折算风速达到11左右后,涡脱频率显著大于结构频率,锁定现象消失。d)折算风速在10.3~11.0之间又可细分为两种情况:一是小风速下结构频率大于名义涡脱频率时,结构频率会受涡脱频率的影响而有所减小,涡脱频率又受结构频率的影响而增大;二是大风速下结构频率小于名义涡脱频率时,结构频率会受涡脱频率的影响而有所增大,涡脱频率受结构频率的影响而减小。
6 结论本文初步总结了大高宽比超高层建筑的涡激振动问题,目的是将涡振的几个现象集中在一起做一个系统展示。囿于篇幅限制,本文未能对各个现象做深入分析,细化分析将在作者其他文章中分别展开。本文结论如下:
1) 在共振临界风速附近,位移时程的简谐性达到最强,但远非理想的简谐振动,呈现为“间歇性共振不稳定共振”。
2) 高层建筑涡致振动过程中,涡振对体系频率的影响不可忽略,振动体系频率随折算风速呈“V”字形变化,在某些情况下频率改变量与自振频率的比值达到10%的量级。
3) “锁定现象”并不是体系振动频率完全“俘获”涡脱频率,而是表现为体系频率与涡脱频率,保持相互影响、相互吸引的动态相等趋势。
| [1] |
梁枢果, 顾明, 张锋, 等. 三角形截面高柔结构横风向振动的风洞试验研究[J]. 空气动力学学报, 2000, 18(02): 172-179. DOI:10.3969/j.issn.0258-1825.2000.02.007 (  0) 0) |
| [2] |
Vickery B J, Stekley A. Aerodynamic damping and vortex excitation on an oscillating prism in turbulent shear flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49: 121-140. DOI:10.1016/0167-6105(93)90009-D (  0) 0) |
| [3] |
王磊, 梁枢果, 张振华, 等. 超高层建筑横风向气动阻尼比简化估算方法研究[J]. 工程力学, 2017, 34(1): 145-153. (  0) 0) |
| [4] |
Larsen A. A generalized model for assessment of vortex-induced vibration for flexible structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57: 281-294. DOI:10.1016/0167-6105(95)00008-F (  0) 0) |
| [5] |
全涌, 顾明, 黄鹏. 超高层建筑通用气动弹性模型设计[J]. 同济大学学报, 2001, 29(1): 122-126. (  0) 0) |
| [6] |
王磊, 梁枢果, 邹良浩, 等. 超高层建筑多自由度气弹模型的优势及制作方法[J]. 振动与冲击, 2014, 33(17): 24-30. (  0) 0) |
| [7] |
Yoshie R, Kawai H, Shimura M. A study on wind-induced vibration of super high rise building by multi-degree-of freedom model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69-71: 745-755. DOI:10.1016/S0167-6105(97)00202-X (  0) 0) |
| [8] |
Tamura Y, Suganuma S. Evaluation of amplitude-dependent damping and natural frequency of buildings during strong winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59: 115-130. DOI:10.1016/0167-6105(96)00003-7 (  0) 0) |
| [9] |
王磊, 梁枢果, 邹良浩, 等. 超高层建筑涡振过程中体系振动频率[J]. 浙江大学学报, 2014, 48(5): 805-812. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35

