过去几十年中,全球风力发电装机容量呈指数型快速增长,其原因不仅是每年新增了大量风场,更为重要的是单一风力发电机组的输出功率显著增加。目前在海上风电场6-8MW机组已被安装试运营,其最大叶片长度已超过80m,叶片尺寸的增加和轻量化设计,使得弯曲与扭转耦合效应更为明显[1]。引入结构弯扭耦合设计的叶片能够被动地减轻风致脉动载荷,是延长叶片疲劳寿命最具成本效益的一种方式[2]。美国Sandia国家实验中心对弯扭耦合自适应叶片进行了研究,其利用叶片在旋转平面内的弯曲来强化叶片的耦合特性,通过外场试验结果发现在低于额定风速下,该叶片能够提高发电功率5%~8%, 并且在高风速下能够降低叶片运行时的脉动载荷[3]。
同时叶片为细长结构,其前几阶振动呈现梁结构特性,采用更为复杂的体单元或壳单元进行有限元建模,对叶片动态响应的计算精度并无明显提高[4]。而精确的叶片截面特性与一维梁单元结合,可以得到和三维有限元法相似的计算精度[5],并具有更好的计算效率。近年来,国外学者对复合材料梁结构的截面特性进行了较多的研究,PreComp[6],VABS[7],FAROB[8],CROSTAB[9]和BPE[10]等方法在风力机叶片截面性能计算中较常被采用。Chen Hui[11]简要叙述了各方法的基础理论,并指出了各自的优缺点,发现采用VABS方法得到的惯性和刚度值与弹性理论计算结果几乎相同,最大误差小于0.19%。Hodges等[12]的研究也同样证明了VABS方法的求解精度。
本文首先采用VABS方法计算了在旋转平面内发生弯曲的叶片,其各截面的惯性、刚度以及在不同方向上的耦合关系。并结合空间一维欧拉-伯努利梁模型,分析了不同的预弯幅度对叶片弯扭耦合情况的影响。同时,采用非定常叶素动量理论[13]并考虑动态入流和动态失速等模型计算气动载荷,并耦合结构模型,分析了预弯幅度不同的叶片在相同控制策略下各风速对应的气动功率,以及在极端阵风条件下的气动弹性响应情况。
1 方法描述 1.1 截面特性计算方法针对复合材料梁结构的截面特性计算,各方法中VABS方法不存在其他方法所提出的假设条件,在数学理论上最为严谨并且具有很好的通用性。VABS方法以包括材料、几何等所有细节的有限元网格形式对截面进行描述,能够得到精确的截面特性,同时由梁模型的结果能够计算出截面任意点的位移、应变和应力情况。
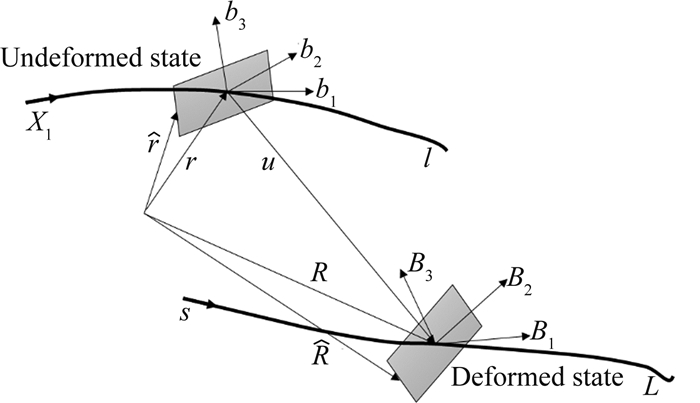
为分析一个复合材料梁结构,需要指定一个参考线l和基于此的正交坐标系bi,其中b1指向参考线的切线方向,如图 1所示。横截面上任意离散点的位置向量可以表示为:
| $ \mathit{\boldsymbol{\hat r}}({\mathit{x}_1},{\mathit{x}_2},{\mathit{x}_3}) = \mathit{\boldsymbol{r}}({\mathit{x}_1}) + {x_a}{\mathit{\boldsymbol{b}}_\alpha }\left( {{x_1}} \right) $ | (1) |
|
图 1 梁变形示意图 Figure 1 Schematic of beam deformation |
当梁结构发生变形时,坐标系bi旋转到新的位置Bi。若考虑剪切变形,变形中B1将不再沿参考轴线方向。为求解方便,引入与梁变形相关的另一个坐标系Ti,其中T1相切于变形后的梁参考线。变形后对应离散点的位置向量表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{\hat R}}\left( {{\mathit{x}_1},{\mathit{x}_2},{\mathit{x}_3}} \right) = \mathit{\boldsymbol{R}}({\mathit{x}_1}) + {x_a}{\mathit{\boldsymbol{T}}_\alpha }\left( {{x_1}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{w_i}({\mathit{x}_1},{\mathit{x}_2},{\mathit{x}_3}){\mathit{\boldsymbol{T}}_i}\left( {{x_1}} \right) \end{array} $ | (2) |
式中R为参考线上点在变形后的位置向量,wi为翘曲位移。
式(2) 中,由于考虑了截面翘曲引进了4次冗余,需要在位移边界条件上给出4个合适的约束。
| $ \left\langle {\left\langle {{w_i}} \right\rangle } \right\rangle = 0 $ | (3) |
| $ \left\langle {\left\langle {{x_2}{w_3} - {x_3}{w_2}} \right\rangle } \right\rangle = 0 $ | (4) |
式中〈〈·〉〉=0表示对整个截面进行积分。
基于对旋转张量的分解概念,小转动的柯西应变分量可表示为:
| $ {\mathit{\Gamma }_{ij}} = \frac{1}{2}({\mathit{\Gamma }_{ij}} + {F_{ji}}) - {\delta _{ij}} $ | (5) |
式中Fij为变形梯度张量,δij为基坐标张量。截面应变能或者梁的应变能密度为:
| $ U = \frac{1}{2}\left\langle {{\mathit{\Gamma }^{\rm{T}}}\zeta \mathit{\Gamma }} \right\rangle $ | (6) |
式中
欧拉-伯努利梁模型,忽略了截面的剪切变形,但能够处理拉伸、扭转和弯曲方向的应变能。
| $ U = \frac{1}{2}{\left\{ {\begin{array}{*{20}{c}} {{\gamma _{11}}}\\ {{\kappa _1}}\\ {{\kappa _2}}\\ {{\kappa _3}} \end{array}} \right\}^{\rm{T}}}\left( {\begin{array}{*{20}{c}} {EA}&{{S_{12}}}&{{S_{13}}}&{{S_{14}}}\\ {{S_{12}}}&{GJ}&{{S_{23}}}&{{S_{24}}}\\ {{S_{13}}}&{{S_{23}}}&{E{I_{22}}}&{{S_{34}}}\\ {{S_{14}}}&{{S_{24}}}&{{S_{34}}}&{E{I_{33}}} \end{array}} \right)\left\{ {\begin{array}{*{20}{c}} {{\gamma _{11}}}\\ {{\kappa _1}}\\ {{\kappa _2}}\\ {{\kappa _3}} \end{array}} \right\} $ | (7) |
式中γ11、κ1、κ2、κ3分别为拉伸应变、扭转应变和绕x2、x3轴的弯曲应变。由式(6) 和式(7) 可以推导得到欧拉梁模型的截面特性,式(7) 矩阵中对角线上EA、GJ、EI22、EI33分别为对应的拉伸刚度、扭转刚度和两个方向的弯曲刚度,非对角线上为两个方向上的耦合刚度。
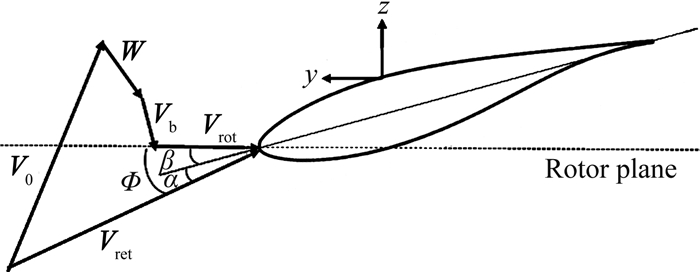
1.2 气动载荷计算方法叶素动量理论(BEM)是风力机非定常气动载荷计算的常用方法,在精确的翼型数据基础上,采用一些必要的修正,BEM方法能够得到较好的计算结果。本文采用该方法,并考虑了Prandtl叶尖损失修正[14]、动态入流模型和动态失速模型。图 2给出了叶片截面相对速度分量的示意关系,各分量的等效和速度Vrel由下式给出。
| $ \left( \begin{array}{l} {V_{{\rm{rel,}}\mathit{y}}}\\ {V_{{\rm{rel,}}\mathit{z}}} \end{array} \right) = \left( \begin{array}{l} {V_{{\rm{0,}}\mathit{y}}}\\ {V_{{\rm{0,}}\mathit{z}}} \end{array} \right) + \left( {\begin{array}{*{20}{c}} {{V_{{\rm{rot}}}}}\\ 0 \end{array}} \right) + \left( \begin{array}{l} {W_\mathit{y}}\\ {W_\mathit{z}} \end{array} \right) + \left( \begin{array}{l} {V_{\mathit{b}{\rm{,y}}}}\\ {V_{\mathit{b}{\rm{,}}\mathit{z}}} \end{array} \right) $ | (8) |
|
图 2 截面速度分量示意图 Figure 2 Velocity triangle seen locally on a blade |
式中V0为入流速度,Vrot为旋转速度,W为诱导速度,Vb为叶片截面处的振动速度。
从整体考虑,风轮的作用像一个圆盘,空气流过后产生不连续的压力降。该压力降所产生的推力导致一个垂直于风轮平面的诱导速度Wn和旋转面内诱导速度Wt,表达式为:
| $ {W_n} = \frac{{ - BL\cos \phi }}{{4\rho \pi rF\left| {{\mathit{\boldsymbol{V}}_0} + {f_g}\mathit{\boldsymbol{n}}\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{W}}} \right)} \right|}} $ | (9) |
| $ {W_t} = \frac{{ - BL\sin \phi }}{{4\rho \pi rF\left| {{\mathit{\boldsymbol{V}}_0} + {f_g}\mathit{\boldsymbol{n}}\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{W}}} \right)} \right|}} $ | (10) |
式中,B为叶片数,L为由翼型数据得到的升力,ϕ为入流角,ρ为空气密度,r为截面在叶片的径向位置,V0为入流风速, W为诱导速度,n为风轮平面法向单位向量,F为Prandtl叶尖损失修正。
1.3 气弹响应计算方法根据势能理论,考虑梁截面的全部耦合项,推导得到了三维空间两节点梁模型的质量和刚度矩阵。并对风力机叶片进行结构有限元离散,按离散拓扑结构构建其质量矩阵M,刚度矩阵K,阻尼矩阵C采用比例阻尼得到。叶片动力学方程可写为
| $ \mathit{\boldsymbol{M\ddot a}}\left( t \right) + \mathit{\boldsymbol{C\dot a}}\left( t \right) + \mathit{\boldsymbol{Ka}}\left( t \right) = \mathit{\boldsymbol{F}}\left( t \right) $ | (11) |
式中右端项F表示由非定常气动载荷、重力载荷和离心载荷构成的载荷向量。
为了过滤式(11) 中的高频项,提高算法的收敛效果,采用了Newmark隐式积分算法。从时间t到t+dt,NewMark算法采用了下列假设。
| $ {{\dot a}_{t + {\rm{d}}t}} = {{\dot a}_t} + \left[ {\left( {1 - \delta } \right){{\ddot a}_t} + \delta {{\ddot a}_{t + {\rm{d}}t}}} \right]{\rm{d}}\mathit{t} $ | (12) |
| $ {a_{t + {\rm{d}}t}} = {a_t} + {{\dot a}_t}{\rm{d}}\mathit{t} + \left[ {\left( {\frac{1}{2} - \alpha } \right){{\ddot a}_t} + \alpha {{\ddot a}_{t + {\rm{d}}t}}} \right]{\rm{d}}{\mathit{t}^2} $ | (13) |
式中α和δ为控制精度和稳定性的参数。
由式(12) 和(13),在t+dt时刻的加速度可表示为
| $ {{\ddot a}_{t + {\rm{d}}t}} = \frac{1}{{\alpha {\rm{d}}{\mathit{t}^2}}}\left( {{a_{t + {\rm{d}}t}} - {a_t}} \right) - \frac{1}{{\alpha {\rm{d}}\mathit{t}}}{{\dot a}_t} - \left( {\frac{1}{2\alpha} - 1} \right){{\ddot a}_t} $ | (14) |
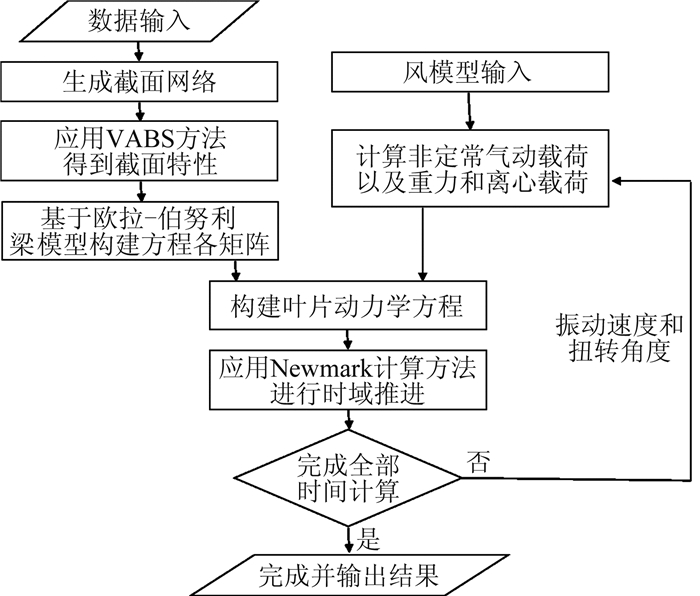
风力机叶片气动弹性响应计算的详细流程如图 3所示。
|
图 3 气弹响应计算流程 Figure 3 Flowchart of the aeroelastic model |
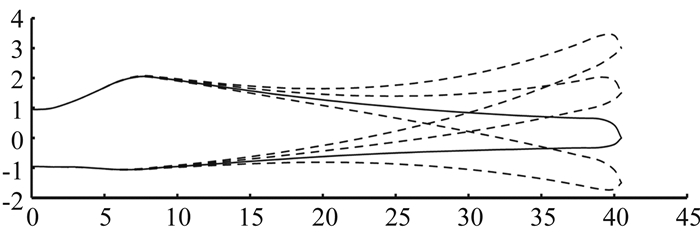
采用了一变速变桨型风力机作为计算模型,其叶片长度为40.5m,在风速10.4m/s、转速17.2r/min时,其达到1.5MW额定功率。在此模型基础上,分别将叶片的叶尖前掠1.5m、后掠1.5m和后掠3.0m,其它截面在旋转平面内的弯曲位移按叶片自身挥舞方向的预弯大小等比例缩放(图 4)。
|
图 4 面内弯曲叶片弦线分布示意图 Figure 4 Schematic of the blade bending in the rotational plane |
图 5给出了采用VABS方法计算叶片前掠(D_tip=1.5m)和两种后掠(D_tip=-1.5m、D_tip=-3.0m)状态下,截面刚度的部分项与原始叶片值的对比情况。其中E33为挥舞方向刚度、S23为扭转与挥舞方向耦合刚度、S24扭转与摆振方向耦合刚度以及S34挥舞与摆振方向耦合刚度。相对于叶片长度,叶尖弯曲产生的位移较小,使得在三种情况下各截面的曲率都较小。从图中总体上可以看出,旋转平面内的弯曲对截面的各方向刚度存在一定的影响,但幅度较小。特别针对弯曲、挥舞等单一方向的刚度,叶片弯曲对其影响非常小,从图 5的第一幅图可以看出,在叶尖后掠3.0m情况下,E33的最大偏差仅为0.36%。截面弯扭耦合刚度相对于单一方向的影响稍微增大,但总体上弯曲的影响也较小。但是从图 5最后一幅图可以看出,叶片在旋转平面内的弯曲对挥舞-摆振方向的弯-弯耦合项影响较大,叶尖弯曲3m状态下,叶片中部的挥舞-摆振耦合刚度偏差接近5.7%。产生上述差异的主要原因是弯扭耦合主要取决于复合材料的方向,旋转平面内的弯曲对其影响较小;而弯-弯耦合不仅与材料方向有关,更与叶片截面的弯曲中心位置有关。
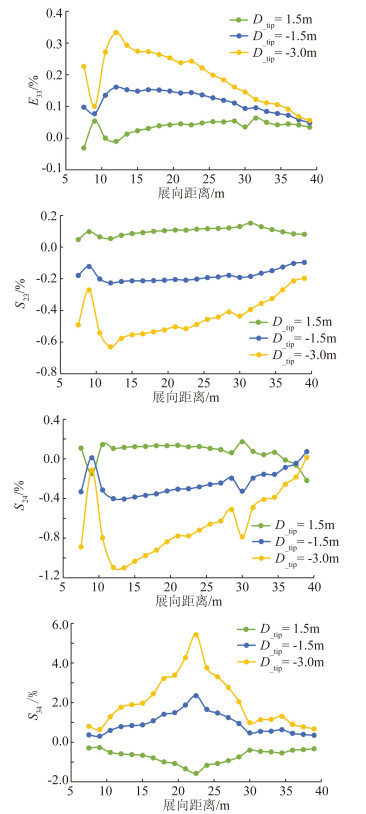
|
图 5 截面刚度相对变化量 Figure 5 Relative variation of sectional stiffness |
本文针对旋转平面内的弯曲问题,计算分析了不同的弯曲幅度对叶片固有频率和振型的影响。图 6给出了不同弯曲幅度下叶片的前两阶固有频率。可以看到,不同弯曲幅度得到的固有频率几乎完全相同,相对误差在0.2%以内。其原因是在对风力机叶片这样细长梁结构进行动力学分析时,挥舞和摆振单一方向的惯性、刚度对前几阶模态起主要作用。从2.1节的计算结果可以看出,旋转平面内不同的弯曲幅度对挥舞、摆振方向的惯性影响较小,这使得叶片的固有频率几乎完全相同。但是对于不同弯曲叶片,其在空间的三维模型发生了改变,各耦合项在单元向全局坐标系变换时发生较为明显的改变,图 7给出了矩阵按质量归一化后前两阶振型在扭转方向分量的对比,单位为弧度。与固有频率以及主方向振型变化都很小不同,前掠或后掠引起的弯扭耦合效应使得叶片前几阶模态在扭转方向的分量存在非常大的差异。叶片后掠增强的弯扭耦合效应,将使叶片向顺桨方向产生更大的扭转变形。同时从图 7中可以看出,模态在扭转方向的分量与弯曲幅度几乎呈现线性关系。
|
图 6 叶片固有频率 Figure 6 Natural frequency of the blade |
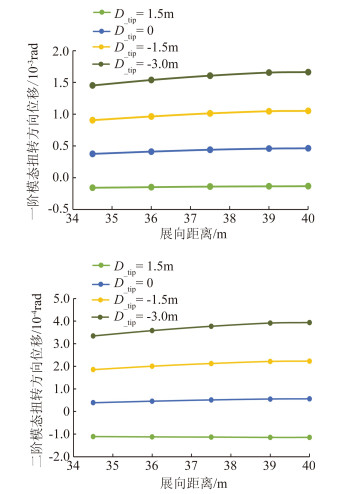
|
图 7 模态扭转方向位移 Figure 7 Torsional displacement of the first two mode |
叶片前掠或后掠增强了弯扭耦合效应,其产生的顺桨或逆桨方向的扭转将直接影响机组的气动功率,图 8给出了在相同变桨变速控制策略下机组的气动功率情况。图中棱型点为软件Bladed计算结果、虚线为不考虑弯扭耦合作用的程序计算值。可以看出在相同计算状态下,程序与Bladed具有非常好的吻合度,验证了结构、气动等模型的准确性。图中D_tip =0m为原叶片在考虑弯曲-扭转耦合状况下的计算结果,可以看出耦合作用导致叶片产生了顺桨方向的扭转,从而使得功率相对减小。并且随着风速的增大,叶片在挥舞方向弯曲位移增大导致顺桨扭转角度增大,与不考虑弯扭耦合时的结果偏差更大。针对旋转平面内弯曲的叶片,可以看出叶片前掠会使得功率增大,而后掠会使得功率降低,这与图 7中给出了耦合模态特性相吻合。
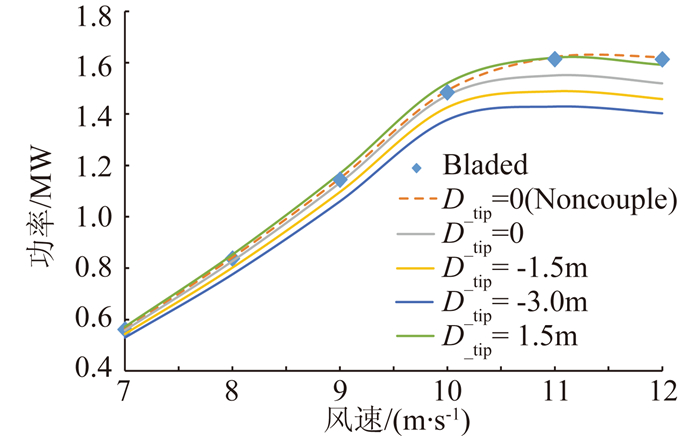
|
图 8 功率随风速变化 Figure 8 Wind power changes with the wind speed |
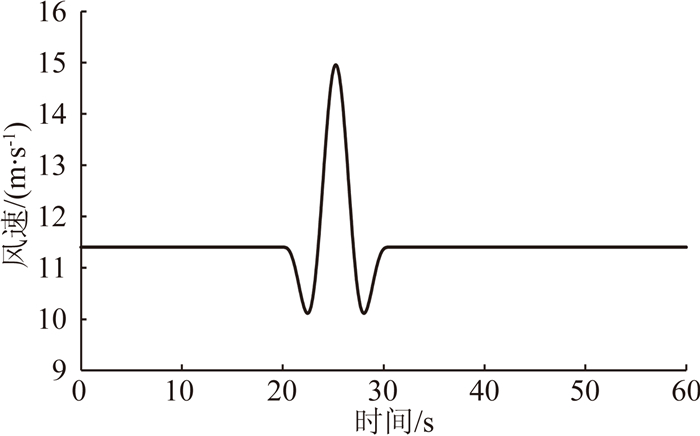
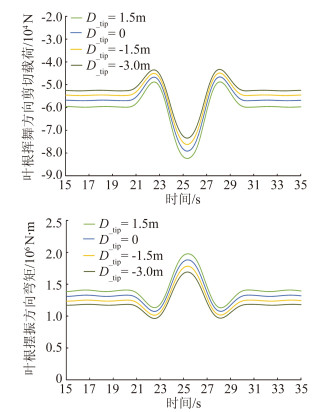
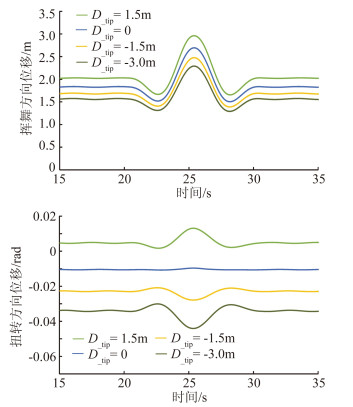
根据风力机设计认证标准GL2003版,选取额定风速为11.4m/s时的极端阵风对叶片进行气弹仿真分析。模拟时间取60s,阵风开始时间为第20s,周期为10.5s,极端运行阵风工况中风速随时间的变化曲线如图 9所示。图 10和图 11给出了各叶片在极端阵风中叶根载荷和叶尖位移变化情况,针对各叶片,同样采用了相同的变速变桨策略。图中首先可以看出叶片的后掠会使叶根载荷以及叶尖位移减小,这与2.2节中的结果相同。其次,从图 10中还可以看到在阵风脉动中,后掠叶片的载荷幅值变化相对较小。表 1给出了前掠或后掠时,在阵风下载荷的最大值与稳态风时平均值相差的幅值,以及与原叶片相差幅值的对比情况。在后掠3m时,叶根挥舞方向剪切载荷波动幅值相对于原叶片下降6.06%,而摆振方向弯矩下降了9.27%,可以看到后掠叶片可以有效降低风力机在极端阵风情况下的载荷波动情况。
|
图 9 阵风中风速随时间变化曲线 Figure 9 Wind velocity curve of gust changes with time |
|
图 10 叶根载荷 Figure 10 Loads at the blade root |
|
图 11 叶尖位移 Figure 11 Displacements of the blade tip |
| 表 1 载荷相对偏差 Table 1 Relative deviation of loads |
|
|
本文研究了旋转平面内的弯曲对风力机叶片的动力学性能以及在极端阵风状况下对气弹响应的影响,得到如下结论:
1) 叶片旋转平面内弯曲引起的曲率较小,对叶片截面特性的影响相对较小,仅对挥舞-摆振方向的耦合刚度具有较为明显的改变;
2) 弯曲对叶片前几阶的固有频率以及振型主方向位移的影响可以忽略,但扭转方向上区别较大,扭转方向模态振型与弯曲位移呈近线性变化;
3) 在相同控制策略下,后掠能够降低叶片在极端阵风下的载荷波动,对疲劳性能具有有益的影响,但同时使得机组的发电功率下降。
| [1] |
Hayat K, De Lecea A G M, Moriones C D, et al. Flutter performance of bend-twist coupled large-scale wind turbine blades[J]. Journal of Sound and Vibration, 2016, 370: 149-162. DOI:10.1016/j.jsv.2016.01.032 (  0) 0) |
| [2] |
Capuzzi M, Pirrera A, Weaver P M. A novel adaptive blade concept for large-scale wind turbines. Part Ⅰ:Aeroelastic behaviour[J]. Energy, 2014, 73:15-24. http://www.sciencedirect.com/science/article/pii/S0360544214004861
(  0) 0) |
| [3] |
Thomas D Ashwill, Gary Kanaby, Kevin Jackson, et al. Development of the sweep-twist adaptive rotor(STAR) Blade[J]. AIAA Journal, 2010. (  0) 0) |
| [4] |
Malcolm D J, Laird D L. Extraction of equivalent beam properties from blade models[J]. Wind Energy, 2007, 10(2): 135-157. DOI:10.1002/(ISSN)1099-1824 (  0) 0) |
| [5] |
Yu W. Efficient high-fidelity simulation of multibody systems with composite dimensionally reducible components[J]. Journal of the American Helicopter Society, 2007, 52(1): 49-57. DOI:10.4050/JAHS.52.49 (  0) 0) |
| [6] |
Bir G S. User's guide to Pre Comp (pre-processor for computing composite blade properties). Technical Report NREL/TP-500-38929. National Renewal Energy Laboratory 2006.
(  0) 0) |
| [7] |
Yu W, Hodges D H, Volovoi V, et al. On Timoshenko-like modeling of initially curved and twisted composite beams[J]. International Journal of Solids & Structures, 2002, 39(19): 5101-5121. (  0) 0) |
| [8] |
Philippidis T P, Vassilopoulos A P, Katopis K G, et al. THIN/PROBEAM:a software for fatigue design and analysis of composite rotor blade[J]. Wind Engineering, 1996, 20: 349-362. (  0) 0) |
| [9] |
Lindenburg C. STABLAD-stability analysis tool for anisotropic rotor blade panels[R]. Technical Report ECN-CX-99-031 r1. Energy Research Center of the Netherlands 2008.
(  0) 0) |
| [10] |
Myrent N J, Bilal N, Adams D, et al. Aerodynamic sensitivity analysis of rotor imbalance and shear web disbond detection strategies for offshore structural health prognostics management of wind turbine blades[J]. AIAA Journal, 2014, 50(6): 623-636. (  0) 0) |
| [11] |
Chen H, Yu W B, Capellaro M. A critical assessment of computer tools for calculating composite wind turbine blade properties[J]. Wind Energy, 2010, 13(6): 497-516. (  0) 0) |
| [12] |
Hodges D H, Yu W. A rigorous, engineer-friendly approach for modelling realistic, composite rotor blades[J]. Wind Energy, 2007, 10(2): 179-193. DOI:10.1002/(ISSN)1099-1824 (  0) 0) |
| [13] |
陈佳慧, 王同光. 考虑气动弹性的风力机叶片性能分析[J]. 空气动力学学报, 2011, 29(3): 396-400. (  0) 0) |
| [14] |
Shen W Z, Mikkelsen R, Sørensen J N, et al. Tip loss corrections for wind turbine computations[J]. Wind Energy, 2005, 8(4): 457-475. DOI:10.1002/we.153 (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


