高超声速风洞是进行高超声速飞行气动试验和研究的重要地面设备,对于暂冲吹吸式高超声速风洞,扩压器的主要作用是在总压损失尽可能小的条件下将超声速气流减速增压以提高扩压器出口压力,减小由于下游背压不断升高对风洞流场带来的影响,维持高超声速风洞在尽可能长的时间内正常运行[1]。
高超声速风洞扩压器通常设计成“收缩段-等直段-扩张段”的组合形式,其中等直径段称为高超声速风洞的第二喉道。试验中扩压器内部存在着激波/激波干扰、激波/附面层干扰诱导的复杂流场,当干扰强烈时, 激波与附面层相交的区域内出现分叉结构, 气流在流动中呈现出减速-加速-再减速的状况, 并形成激波串结构。早在20世纪50年代,Neumann和Lustwerk等就在探索超声速风洞设计过程中就已经得到了管道内激波串的试验观察结果[2-3]。Rudolf Hermann通过数值和试验方法研究了自由射流超声速风洞扩压器效率和扩压器内流场[4]。Deepak等进行了ⅡSc高超声速风洞马赫数8.0条件下扩压器内流场的数值模拟和试验研究,结果显示试验与数值模拟得到的流场特征符合较好[5]。近年来国外对扩压器设计,扩压器性能以及风洞流场特征进行了较为深入的研究,得到大量的数值模拟和试验结果[6-9]。国内李桦等和陈吉明等对扩压器内激波串结构进行数值模拟,较好模拟了扩压器中由激波/边界层干扰诱导的复杂流场的流场特性[10-11]。陈立红等通过试验研究了扩压器几何形状、安装位置以及长度对风洞起动过程流动状态的影响,探索了扩压器的优化设计[1]。童华等采用试验方法研究了某高超声速风洞扩压器性能[12]。
但由于扩压器内流动非常复杂, 并且扩压器不是一个孤立的部件,必须结合整座风洞实际进行分析研究,扩压器设计还未见成熟系统的理论和方法。本文采用一维管流方法对口径Φ240mm、马赫数6.0的自由射流高超声速风洞扩压器进行设计,通过数值模拟方法对扩压器结构形式进行筛选,采用试验与数值模拟方法研究扩压器流场结构和性能,为自由射流高超声速风洞扩压器的设计提供参考。
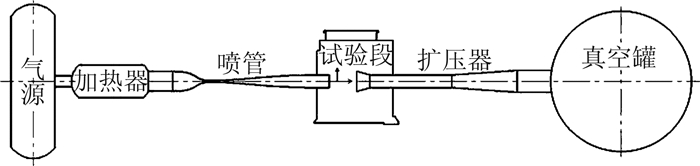
1 理论分析图 1为暂冲吹吸式自由射流高超声速风洞示意图。风洞开始运行时,真空罐内压力较低,能够保证风洞起动压比;但随着试验的进行,真空罐的压力逐渐增大,假设没有扩压器的情况下,必然使试验段压力逐渐增大,喷管出口射流由欠膨胀状态过渡到过膨胀状态,最终导致风洞流场建立失败。故而需要扩压器在风洞运行过程将喷管出口射流控制在收气锥内,通过扩压器将主流气体排出,使试验段维持在低压状态,在真空罐压力不断上升的情况下尽可能长时间维持风洞正常运行。
|
图 1 暂冲吹吸式自由射流高超声速风洞示意图 Figure 1 Intermittent blow-down hypersonic wind tunnel |
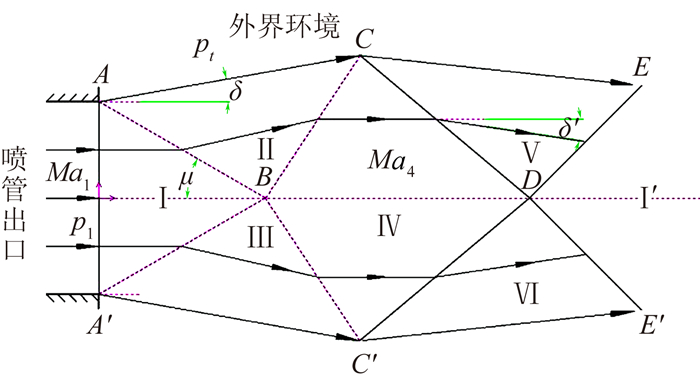
气动中心超高速所拟研制一座口径Φ240mm、马赫数6.0的高超声速研究型风洞,需要进行与喷管和试验状态相匹配的扩压器气动设计。在扩压器设计过程中,扩压器入口几何形状和尺寸、扩压器与喷管相对位置、压缩形式和角度、第二喉道直径和长度等都是扩压器设计的关键参数[8, 13]。本文涉及的高超声速风洞喷管为轴对称型面喷管,故选择轴对称形状扩压器与之匹配。根据轴对称低度欠膨胀自由射流的工程算法得到喷管射流的基本特征,综合考虑风洞实际和已有扩压器设计经验,确定扩压器入口尺寸和距离喷管出口距离。图 2为典型轴对称低度膨胀自由射流流动结构[14]。
|
图 2 轴对称低度欠膨胀自由射流流动结构 Figure 2 Structure of axisymmetric under-expanded free jet |
如图 2所示,喷管出口压力pe高于外界(试验段)环境压力pt时,喷管出口气流在核心区(ABA′)内参数保持不变,其中AB和A′B为马赫线,马赫角μ=arcsin(1/Ma)。在工程近似计算中,气流经过马赫线后产生膨胀,气流向外折转一个角度δ,可通过上游总压p0,喷管出口静压pe以及外界压力pt计算得到,并且得到Ma2和Ma3。由Ⅱ(Ⅲ)区进入Ⅳ区,气流必须内折一个δ,使气流方向恢复到I区的方向,否则B点将形成真空,气流进一步膨胀,根据折转角,计算(或查表)得到Ma4以及p4/p0。气流由Ⅳ进入Ⅴ(Ⅵ)区之前经过两次膨胀,静压已低于环境压力,因此要受压缩向内折转一个δ′角。CD和C′D可认为是弱压缩波,它们在D点相交后仍要产生压缩波DE和DE′,所以再次产生一个折角δ′,气流方向改为水平,静压高于环境压力pt。接着气流像上述Ⅰ区~Ⅰ′区(称作一个波节)一个波节接着一个波节的流动下去,实际过程中流动是有能量损失的,射流流动会产生衰减,波节最终消失[14]。
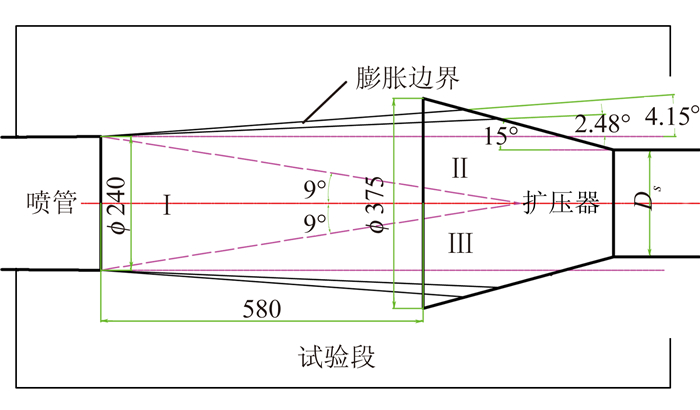
扩压器设计过程中,涉及图 2中的气流区域有Ⅰ、Ⅱ、Ⅲ、Ⅳ区。假定风洞来流条件为p0=0.8MPa,T0=438.5K,喷管喉道直径Φ28.66mm,出口直径Φ240mm,根据理想等熵关系得到出口马赫数Ma1=6.39,静压pe=340Pa,马赫角约为9°,普朗特-迈耶尔角(PM角)为87.55°。假设喷管出口静压与试验段内压力的压比pe/pt分别是1.5和2.0,这样得到图 1中Ⅱ(Ⅲ)区的状态如表 1所示, 根据表 1的数据,初步确定扩压器入口尺寸和与喷管出口的距离,如图 3所示。
|
图 3 扩压器设计示意图(mm) Figure 3 Design configuration of the diffuser(Unit: mm) |
| 表 1 不同压比得到的膨胀折角 Table 1 PM angle of vary pressure ratio |
|
|
为便于不同结构形式扩压器之间的比较,先假定扩压器入口距离喷管出口580mm保持不变,扩压器入口直径为Φ375mm,约为1.56De。从图 3中可以看出,不同压比条件下膨胀边界均在收气锥之内。
对于收气锥的结构形式,首先选取单级压缩半锥角为15°的扩压器压缩形式,固定第二喉道长度(2200mm左右),对比研究第二喉道直径对于扩压器性能的影响;随后再研究不同压缩结构的扩压器性能,最终筛选出扩压器设计方案。
根据《高速风洞试验》[15]提供的第二喉道面积计算公式:
| $ \frac{{{A_s}}}{{{A_e}}} = \frac{{{{\left( {5 + M{a^2}} \right)}^{0.5}}{{\left( {7M{a^2} - 1} \right)}^{2.5}}}}{{216M{a^6}}} $ | (1) |
其中,A为截面面积,下标e代表喷管出口截面,s代表第二喉道截面。该公式的物理意义为:设第二喉道马赫数为1.0,并假定空气在喷管出口通过正激波(波前为喷管出口马赫数)后等熵膨胀到第二喉道时马赫数为1.0。计算得到第二喉道与喷管出口面积比为0.63左右,故选择第二喉道直径为0.8De作为基准,比较0.7De、0.9De、1.0De不同第二喉道直径的扩压器性能。
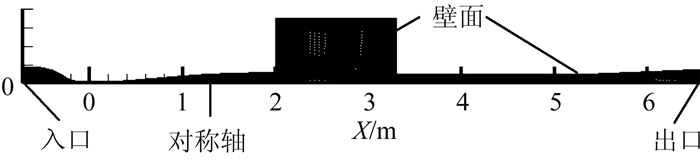
2 数值模拟结果及分析 2.1 网格及边界条件采用层流模型进行数值模拟,计算域包括喷管、试验段以及扩压器,二维结构网格数在16万左右,如图 4所示。
|
图 4 网格示意图 Figure 4 Computational grid |
边界条件设置如下:
入口:p0=0.8MPa,T0=438.5K;
壁面:绝热壁;
出口:压力出口,初始状态pB=500Pa;为确定不同扩压器的抗背压能力,在初始背压条件下计算得到稳定流场基础上,不断提高背压反复进行计算,直到风洞不起动,此时的背压记为风洞不起动的临界背压,同时也表明了扩压器的抗背压能力。
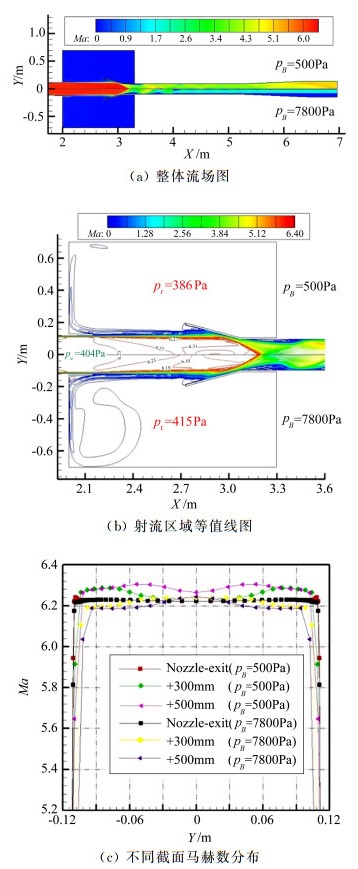
2.2 单级压缩半锥角15°扩压器不同背压条件下单级15°-0.8De扩压器流场结构如图 5所示。由于喷管射流静压与试验段静压基本相等,射流在进入扩压器之前基本为等直圆柱。pB=500Pa条件下,射流在扩压器收气锥内受到压缩,形成的锥形激波在轴线上相交后反射到第二喉道壁面边界层上,出现流动分离,分离泡的存在导致第二喉道内部形成收缩-扩张流道,迫使气流先减速后加速,并在分离泡后形成较强的相交斜激波;随后,气流在第二喉道受到系列斜激波的压缩,但一直处于超声速状态;进入扩压器尾部的扩张段时,气流进一步加速,以超声速气流排出。
|
图 5 15°-0.8De扩压器流场结构 Figure 5 Field flow configuration of 15°-0.8De diffuser with different back pressure |
pB=7800Pa条件下,第二喉道入口处壁面出现流动分离,若分离泡进入收气锥内将会使核心流受到压缩,进而影响风洞的起动,因此此时的背压表征了扩压器能够承受的最大背压。入口处分离泡下游斜激波在X=3.75m处打到壁面边界层形成另一个分离泡,两个分离泡的存在使气流在第二喉道内减速-加速-再减速-再加速,同时在X=4m附近中心区域气流受到类似正激波的压缩形成亚声速气流,在这之后的下游气流大部分处于亚声速状态并排出。
由不同截面的马赫分布图可以看出,喷管出口平均马赫数约为6.23,比理论值6.39小,这是因为边界层存在导致有效膨胀面积比变小,马赫数降低。pB=500Pa时,喷管射流在试验段内略有扩张;而pB=7800Pa时,喷管射流略受压缩,相同截面位置均匀区和平均马赫数较pB=500Pa状态小。
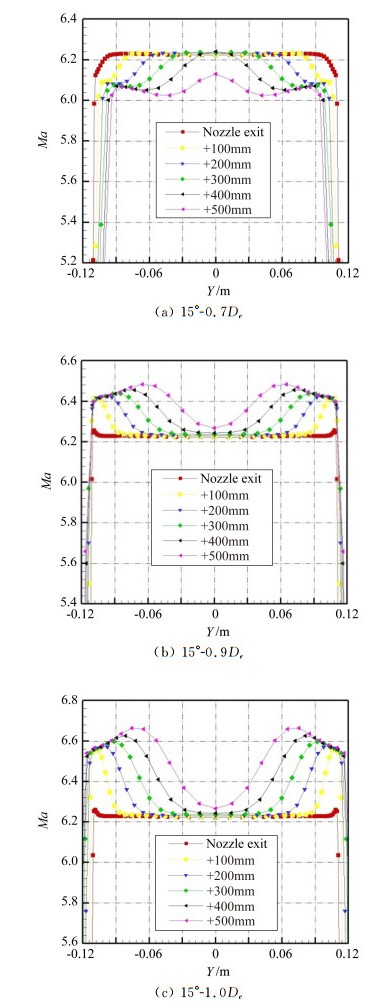
为对比不同第二喉道直径对扩压器性能的影响,在完成单级15°-0.8De扩压器计算后,进行了单级15°-0.7、0.9、1.0De扩压器pB=500Pa以及各自临界背压条件下的计算,图 6为计算得到不同第二喉道直径扩压器在pB=500Pa背压条件下,风洞不同截面的马赫数分布图。需要说明的是,各自临界背压条件下的核心区流场特征与初始背压基本相同,未发生明显的变化。
|
图 6 安装15°-0.7/0.9/1.0De扩压器风洞不同截面马赫数分布(pB=500Pa) Figure 6 Mach number curve of vary section in wind tunnel with 15°-0.7/0.9/1.0De diffusers(pB=500Pa) |
从图 6可以看出,第二喉道直径为0.7De时,喷管射流处于过膨胀状态,射流受到压缩,说明扩压器第二喉道减小,流通能力变弱,对试验段的抽吸减弱,试验段静压高于射流静压,射流受到压缩。第二喉道直径为0.9De和1.0De时,扩压器抽吸能力增强,试验段压力低于喷管射流静压,射流在试验段内发生膨胀,均匀区以外气流马赫数明显增大,第二喉道直径越大扩压器抽吸能力越强,气流膨胀越严重。
根据数值模拟结果得到单级15°压缩不同第二喉道直径的扩压器性能如表 2。
| 表 2 单级15°压缩不同第二喉道直径的扩压器性能 Table 2 Performance of single compression 15° diffusers with vary second throat diameter |
|
|
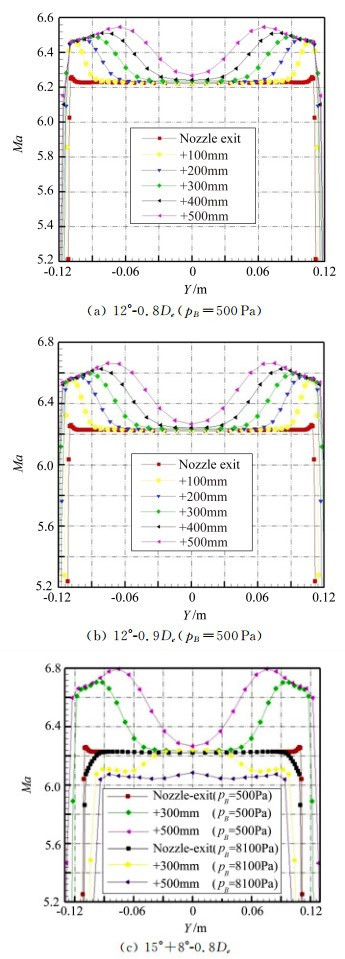
为对比不同压缩半锥角以及压缩锥形式对于扩压器性能的影响,设计单级压缩12°-0.8De和12°-0.9De以及两级压缩锥15°+8°-0.8De扩压器进行对比计算,其余扩压器设计参数保持不变,同样进行pB=500Pa以及临界背压条件下的数值模拟。图 7为计算得到安装不同结构形式扩压器的风洞不同截面马赫数分布图。
|
图 7 安装不同结构扩压器风洞不同截面马赫数分布 Figure 7 Mach number distributions of vary section in wind tunnel with different diffusers |
如图 7所示,单级12°-0.8De、12°-0.9De与双级15°+8°-0.8De扩压器在背压为500Pa条件下的流场结构相似,喷管射流处于欠膨胀状态,但膨胀程度依次递增,说明扩压器抽吸能力呈增强趋势。单级12°-0.8De和12°-0.9De各自临界背压分别为10kPa和9kPa,呈递减趋势,但射流流场特征与初始背压基本相同,未发生明显的变化。
对于双级15°+8°-0.8De扩压器,当背压较小时,扩压器流通能力较强,喷管射流处于膨胀状态,膨胀边界打到第一级压缩锥上;当背压达到临界背压8.1kPa时,射流边界打到第二级压缩锥上,射流在试验段受到压缩,射流流场特征出现较大变化,风洞流场品质不是很理想。
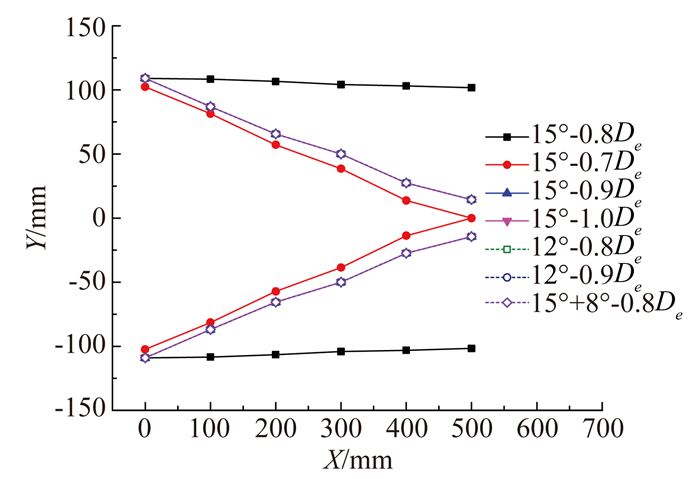
根据数值模拟结果得到不同压缩结构的扩压器性能如表 3,图 8为不同结构扩压器在背压500Pa条件下均匀区大小示意图。
| 表 3 不同压缩结构的扩压器性能 Table 3 Performance of different diffusers |
|
|
|
图 8 不同结构扩压器背压500Pa条件下均匀区示意图 Figure 8 Uniformity area of wind tunnel with different diffusers at pB=500Pa |
根据表 3和图 8可以看出,单级12°-0.8De、12°-0.9De扩压器抗反压能力都强于单级15°-0.8De扩压器,但在临界背压条件下第二喉道出口的总压恢复都低于单级15°-0.8De扩压器。两级压缩15°+8°-0.8De扩压器抗背压能力以及临界背压条件下的总压恢复都大于单级15°-0.8De扩压器,但在临界背压条件下喷管射流受到压缩,流场均匀区偏小。初步确定单级15°-0.8De扩压器为最优方案进行下一步试验验证。
3 试验结果分析为验证扩压器设计方法的有效性,依托气动中心已有的Φ300mm口径的暂冲式高超声速风洞,加工收气锥半锥角为15°,第二喉道直径为Φ240mm(0.8De喷管出口直径)扩压器,进行扩压器流场和性能测试。这样既节省扩压器设计方法的验证周期,同时所加工的扩压器也可作为新风洞(喷管口径Φ240mm)的备选方案。
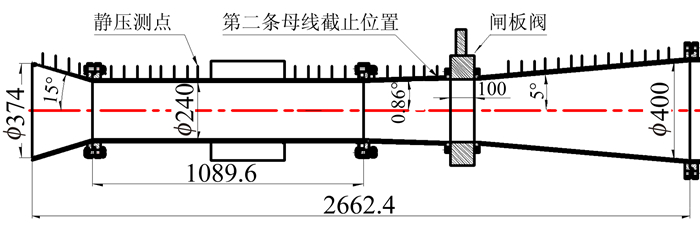
图 9位试验扩压器构型及压力测点布置图。由于扩压器入口直径Φ374mm(约为1.25De)相对较小,将扩压器与喷管出口的距离调整为410mm。扩压器沿轴线方向布置静压测点,分布在两条母线上,第一条母线位于扩压器纵向切面,共有37个测点,同时在扩压器下游布置4个测点监控扩压器背压,第二条母线位于扩压器横向切面,共有23个测点。沿程壁面静压采用电子扫描阀压力测量系统进行测量。实际风洞运行过程中喷管边界层一般处于湍流状态,因此采用κ-ε湍流模型进行数值模拟,计算域包括喷管、试验段以及扩压器,与试验结果进行对比分析,试验与数值模拟状态见表 4。
|
图 9 试验扩压器构型及压力测点布置图(mm) Figure 9 Configuration and pressure tap location of diffuser(Unit: mm) |
| 表 4 试验和数值模拟状态表 Table 4 Test and numerical simulation conditions |
|
|
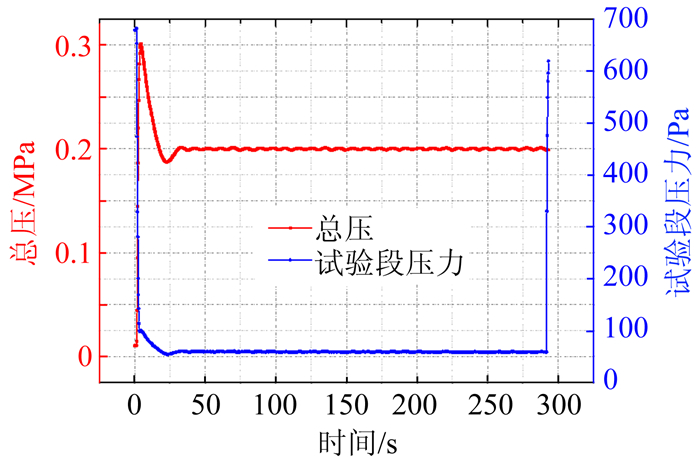
图 10给出了风洞长时间运行的总压和试验段压力曲线。风洞在真空球(2000m3)为680Pa时开始起动,30s后风洞总压/总温调平开始稳定运行,试验段静压维持在60Pa左右,293s后风洞不起动,此时扩压器背压为6.1kPa,理论计算得到真空球压力大约为6.5kPa。
|
图 10 风洞总压和试验段压力随时间的变化曲线 Figure 10 Variation histories of total pressure and test-section pressure |
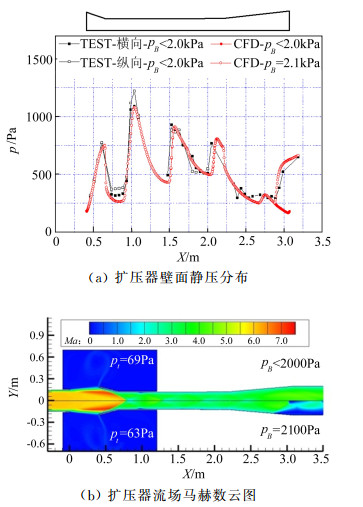
在背压pB≤2100Pa扩压器试验与计算得到的扩压器沿程壁面静压分布以及计算获得的流场结构如图 11所示,横坐标原点位于喷管出口。
|
图 11 低背压状态扩压器壁面压力与流场结构 Figure 11 Wall pressure distributions and flowstructure of diffuser with low back pressure |
低背压条件下,扩压器内气流受到系列斜激波的压缩,大部分气流处于超声速状态,试验和数值模拟对于斜激波串的捕捉吻合较好;但pB < 2000Pa时扩张段尾部计算与试验结果出现一定差异,主要是因为紧接着扩压器的真空管道有一个接近80°的拐弯,从而使试验中扩张段壁面的流动分离相比数值模拟提前,导致扩压器尾部在风洞一起动就出现数值计算在pB=2100Pa时的压力跃升。
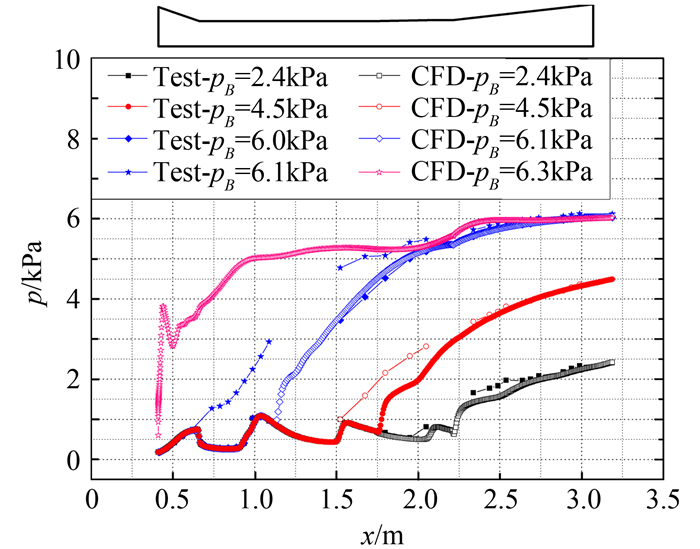
图 12给出了背压pB≥2400Pa扩压器壁面压力曲线分布。随着风洞的持续运行,扩压器背压逐渐升高,壁面的压力跃升位置逐渐前传,说明扩压器内的激波串结构逐渐前传,激波串强度逐渐增强以抵抗扩压器背压的升高,因此壁面压力跃升的幅度越来越大;试验与数值计算结果基本吻合,但在激波串位置的捕捉上出现一定差异,相同背压条件下试验出现激波串结构的位置相比计算更靠近上游,并且最终导致试验中扩压器背压达到6100Pa时风洞不起动,而数值计算风洞可稳定运行到6300Pa,两者偏差3.2%,在可接受范围内。
|
图 12 pB≥2400Pa状态扩压器壁面压力曲线 Figure 12 Wall pressure distributions of diffuser with back pressure greater than 2400Pa |
通过以上分析可以看出,所设计的扩压器能够使风洞正常起动,并且能够长时间维持风洞正常运行,基本达到设计预期。
4 结论采用一维管流方法对口径为Φ240mm、马赫数6.0的自由射流高超声速风洞扩压器进行设计,并通过数值模拟方法对不同压缩形式、压缩锥角以及第二喉道直径的扩压器进行了对比研究,最后通过试验和数值计算研究了筛选得到的扩压器流场特征和性能,通过研究得到以下结论:
1) 对于给定的喷管和来流状态,以单级压缩半锥角15°、第二喉道直径为0.8De的扩压器基准设计方案,喷管射流在试验段内基本处于完全膨胀状态,流场品质良好;对于其余扩压器方案,由于抽吸能力的不同,导致喷管射流处于欠膨胀状态或者过膨胀状态,均匀区都有所减小;
2) 扩压器第二喉道直径影响到扩压器的流通能力,即对试验段的抽吸能力。在压缩形式一定的情况下,在一定范围内,第二喉道直径越小,扩压器流通能力减弱,同时扩压器抗反压能力越强;对于单级压缩锥形式的扩压器,压缩半锥角减小,收气锥对于主流的压缩变弱,损失变小,导致扩压器的抗反压能力有所增强;
3) 单级15°-0.8De形式的扩压器试验与数值计算结果吻合较好;低背压条件下,扩压器内气流主要受到斜激波串压缩,大部分气流处于超声速状态;随着背压的持续升高,激波串结构进入扩压器并前传,激波串结构下游的气流处于亚声速状态;
4) 相同背压条件下,试验出现激波串结构的位置相比计算更靠近上游;同时,试验获得的扩压器临界背压要低于计算结果,但两者偏差较小,在可接受范围内。
综上所述,经过筛选得到的单级15°-0.8De扩压器能够使风洞正常起动,并且能够长时间维持风洞正常运行,达到设计预期,该设计方案可用于新风洞建设。
| [1] |
陈立红, 张新宇, 顾洪斌. 扩压段对高超声速推进风洞起动的影响[J]. 推进技术, 2004, 25(5): 430-434. (  0) 0) |
| [2] |
Neumann E P, Lustwerk F. Supersonic diffusers for wind tunnels[J]. J. Appl. Mech., 1946, 16(2). (  0) 0) |
| [3] |
Neumann E P, Lustwerk F. High-efficiency supersonic diffusers[J]. J. Aeronaut. Sci., 1951, 18(6): 369-374. DOI:10.2514/8.1975 (  0) 0) |
| [4] |
Rudolf Hermann. Diffuser efficiency and flow process of supersonic wind tunnels with free jet test section[R]. Af Technical Report NO.6334, 1950.
(  0) 0) |
| [5] |
Deepak N R, Jagadeesh G, Vasudevan B. Investigations of flow through the diffuser of ⅡSc Hypersonic wind tunnel[R]. AIAA 2006-8155.
(  0) 0) |
| [6] |
Honggye Sung, Sangkyu Yoon, Hyowon Yeom, et al. Study on design-and operation-parameters of supersonic exhaust diffusers[R]. AIAA 2008-855.
(  0) 0) |
| [7] |
Manikanda Kumaran R, Sundararajan T, Raja Manohar D. Performance evaluation of second-throat diffuser for high-altitude-test facility[J]. Propulsion and Power, 2010, 26(2). (  0) 0) |
| [8] |
Junichi Akatsuka, Shinji Nagai. The effect of diffuser geometry on the starting pressure ratio of a supersonic wind tunnel[C]//27th AIAA Aerodynamic Measurement Technology and Grand Testing Conference. Doi:10.2514/6.2010-4344.
(  0) 0) |
| [9] |
Byung Hoon Park, Jihwan Lim, Sunghyun Park, et al. Design and analysis of a second-throat exhaust diffuser for altitude simulation[J]. Propulsion and Power, 2012, 28(5). (  0) 0) |
| [10] |
李桦, 范晓樯, 丁猛. 超声速扩压器中激波串结构的数值模拟[J]. 国防科技大学学报, 2002, 24(1): 18-21. (  0) 0) |
| [11] |
陈吉明, 任玉新. 超音速风洞扩压器激波串现象的数值模拟[J]. 清华大学学报, 2007, 47(5): 264-267. (  0) 0) |
| [12] |
童华, 孙启志, 张绍武. 高超声速风洞扩压器试验研究与分析[J]. 实验流体力学, 2014, 28(3): 78-81, 103. DOI:10.11729/syltlx20120201 (  0) 0) |
| [13] |
Earl H Andrews Jr, Ernest A Mackley. Design, tests, and verification of a diffuser system for a Mach 4 scramjet test facility[J]. Aircraft, 1979, 16(10). (  0) 0) |
| [14] |
赵承庆, 姜毅. 气体射流动力学[M]. 北京理工大学出版社, 1998.
(  0) 0) |
| [15] |
王发祥. 高速风洞试验[M]. 北京: 国防工业出版社, 2003.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35

