概念设计是飞行器设计的早期阶段,需要从众多概念方案中优选出最佳方案。飞行器概念设计中需进行大量气动特性分析,传统的做法是采用工程估算方法快速地分析概念方案的气动特性。目前飞行器概念设计的一个重要趋势是气动分析模型采用数值计算方法[1-2],其优势在于:能提高气动分析模型的预测精度;能应用于非常规布局的气动特性分析。
飞行器概念设计阶段的气动数值分析方法应满足如下要求:1) 外形建模的参数化;2) 计算网格生成的自动化;3) 流场求解速度快、时间短;4) 能适用于不同飞行速度和高度范围。虽然基于N-S方程的数值方法具有计算精度高,通用性强的优点,但所需计算时间仍然较长,目前还难以满足概念设计阶段快速响应要求。
国外已发展了几种面向飞行器概念设计的气动数值分析工具,如APAS[3]和CBAERO[4]。但上述两个工具无法对跨声速气动特性进行较精确的估算。从计算精度和效率上看,在概念设计阶段,基于全速势方程的数值方法具有计算速度快、存储空间占用小的特点,是众多方法中最适用于亚/跨声速计算的工具。目前,典型的基于全速势方程的气动分析程序有FLO[5]、BLWF[6]、TranAir[7]等。其中,FLO只适用于机翼,BLWF只适用于翼身组合体。TranAir采用自适应直角坐标网格和有限元方法,具有较好通用性,但TranAir的使用依赖附加的前处理模块AGPS[8],一定程度上也限制其自动化的程度。
网格生成是CFD中一项重要的内容。结构、非结构和直角网格是常用的几种网格类型,与前两种网格类型相比,直角网格有着空间填充能力强和复杂几何外形适应性好的优点,较容易实现网格的自动生成和自适应加密。从满足概念设计阶段气动计算对网格生成的要求来说,直角网格是值得研究和发展的方法[9-10]。
本文旨在研究和开发一种全速域气动分析的集成工具。亚、跨声速情况,采用全速势方程有限体积解法;超声速情况,采用欧拉方程有限体积解法;高超声速情况,采用基于当地表面斜度法的工程面元法。计算网格采用自适应直角网格。通过集成参数化几何模型、自适应直角网格方法、全速势方法、欧拉方法、工程面元法的程序,形成面向飞行器概念设计的快速气动分析工具。
以下首先阐述气动分析工具的总体框架;然后说明几何模型和计算网格的快速生成方法;之后简述全速势方法、欧拉方法、工程面元法的算法;最后通过算例对各气动分析程序进行验证。
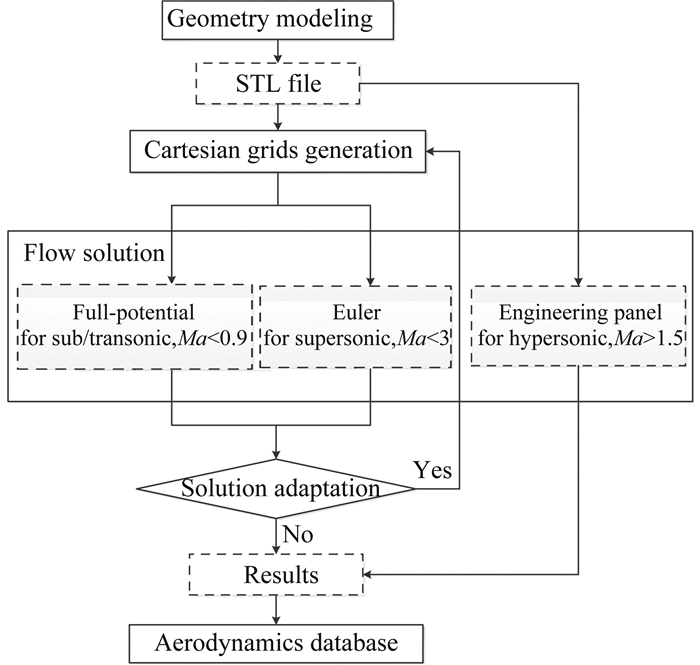
1 气动分析工具的框架本文气动分析工具由外形参数化建模、计算网格生成、流场计算组成,其中流场计算包含全速势方法、欧拉方法、工程面元法。气动分析工具的架构如图 1所示。通过集成各模块,整个过程可自动进行。流程简述如下:
|
图 1 气动分析流程 Figure 1 Aerodynamic analysis procedures |
1) 采用软件Open VSP[11]进行飞行器几何建模,快速生成的几何模型文件(STL格式)。
2) 基于几何外形,采用自适应直角网格方法自动生成全速势和欧拉方法需要的网格。工程面元法则直接读取STL文件作为气动网格。
3) 针对不同来流速度选择计算方法;分析结束后,根据结果的精度,全速势和欧拉方法可自动执行网格自适应,直到得到足够精度的结果。
4) 分析和处理计算结果,输出分析报告和指定格式的数据文件存入飞行器气动数据库。
2 飞行器外形参数化建模Open VSP是一种面向飞行器概念设计的参数化几何建模开源软件,特点如下:1) 与传统CAD软件相比,需要的计算机资源很少;2) 飞行器的几何特征是由设计人员所熟悉的参数来定义的;3) 可快速生成概念方案的几何模型;4) 提供了多种组件来定义飞行器的几何特征,可涵盖各类飞行器的外形建模。
Open VSP创建的飞机几何模型的输出图形格式包括IGS、STL、STEP等,并可计算和输出飞机各部件的外露面积、内部体积等几何特性。同时,应用其脚本功能可实现从EXCEL或XML文件读取给定的几何参数,直接生成模型,并输出指定格式的几何文件。
3 计算网格的自动生成高超工程面元法计算直接基于STL三角片数据进行。全速势和欧拉方程的求解则在自动生成的直角网格上进行,生成过程如下。
3.1 几何模型和数据结构采用外形建模模块生成的STL格式的文件作为几何模型。该格式的文件由包含外法向量信息的三角片组成。通过使用交替数字树数据结构[12]来管理三角片,使得直角网格单元搜索相交三角片的操作能快速进行。
采用八叉树结构定义网格的拓扑关系。完整的直角网格是从包含整个计算域的根节点逐步加密得到的。除根节点外,八叉树中每个单元都是通过加密其父单元得到的。
3.2 网格初始化和几何自适应从八叉树的根节点开始生成初始均匀网格。将树中的每个叶子节点加密,直至所有叶子节点层数加密至设定的初始层数。
显然,初始均匀网格不能精确地描述几何外形,故需要进行几何自适应[9-10]。几何自适应是根据物面边界的复杂程度,通过判断物面边界单元是否需要加密来实现的。
根据几何自适应和后续处理的需要,需将网格单元进行分类。直角网格单元主要分为三类:流场内非切割单元、固壁内非切割单元和物面边界单元。使用交替数字树算法搜索确定与物面相交的单元,即物面边界单元。当所有物面边界单元都判断完毕,流场内外非切割单元便组成了各自的单连通域。非切割单元使用光线投射算法[10]进行类型判断,并使用染色算法快速确定其单连通域内其他单元的类型。
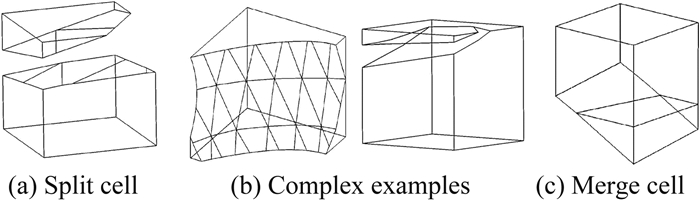
3.3 物面边界单元的处理因为直角网格并不贴体,所以需要对物面边界单元进行处理才能正确的施加物面边界条件。本文使用精度高且发展成熟的切割法[9-10, 13]进行处理。由于物面边界单元和物面边界的相交情况十分复杂,因此八叉树结构无法方便地存储切割后的单元信息,见图 2。例如图 2(a)所示,当单元被分割成多个部分时,八叉树结构就很难描述该拓扑关系了。本文采用“cell-to-face”[14]的数据结构来专门存储物面边界单元,通过网格面存储的两侧单元编号直接提供单元间连接信息。这样不同种类的复杂切割情况能够得到正确的处理,其拓扑关系也能得到正确的存储,如图 2(b)。
|
图 2 物面边界单元的切割情况 Figure 2 Illustration of intersection between CUT-cell and wall boundary |
切割处理后会产生体积极小的单元,从而引起计算的不稳定。故采用网格融合[13]技术将极小单元与较大的邻居单元合并,如图 2(c)所示。
4 数值方法 4.1 全速势方程及离散求解方法 4.1.1 控制方程三维定常全速势方程的守恒形式为:
| $ \nabla \cdot \left( {\rho \mathit{\boldsymbol{V}}} \right) = 0 $ | (1) |
| $ \mathit{\boldsymbol{V = }}(\mathit{u}\;\;\;\upsilon \;\;w) = ({\phi _x}\;\;{\phi _y}\;\;{\phi _z}) $ | (2) |
式中:速度V是速度位ϕ的梯度。ρ是表达式为:
| $ \rho = {\left[ {1 + \frac{{\gamma - 1}}{2}Ma_\infty ^2(1 - {{\left\| V \right\|}^2})} \right]^{\frac{1}{{\gamma - 1}}}} $ | (3) |
其中,γ是比热比,Ma∞是自由来流马赫数。
4.1.2 有限体积空间离散1) 离散格式。将控制方程写成积分形式,由散度定理得到:
| $ \iiint\limits_V {\nabla \cdot (\rho V)}{\rm{d}}V = \iint\limits_V {\rho \mathit{\boldsymbol{V}}} \cdot n{\rm{d}}S = 0 $ | (4) |
对任意单元i,方程(4) 用有限体积法离散为:
| $ \sum\limits_{j = 1}^{{\rm{faces}}} {({\rho _j}{\mathit{\boldsymbol{V}}_j} \cdot {\mathit{\boldsymbol{n}}_j})\Delta {A_j}} = {Res_i} = 0 $ | (5) |
其中,ρj、Vj是单元i的网格面j面心处的密度和速度,nj、ΔAj是网格面j的外法矢和面积,Resi表示单元i的残差。
2) 通量计算。采用文献[15]中的K-exact Least Squares方法构建ϕ的梯度来计算方程(5) 中的Vj。在面心进行梯度构建时,选择面左右单元以及左右单元邻居的值进行插值。每个参与单元的插值多项式为:
| $ {\phi _i} = {C_{0,0,0}} + {C_{1,0,0}}{x_i} + {C_{0,1,0}}{y_i} + {C_{0,0,1}}{z_i} $ | (6) |
式中:xi、yi、zi为单元i中心的坐标。由于参与单元的个数不确定,采用最小二乘法求这四个系数。插值多项式在每个单元上的误差为:
| $ {e_i} = {C_{0,0,0}} + {C_{1,0,0}}{x_i} + {C_{0,1,0}}{y_i} + {C_{0,0,1}}{z_i} - {\phi _i} $ | (7) |
将各单元误差的平方加权求和可得:
| $ F\left( {{C_{0,0,0}},{C_{1,0,0}},{C_{0,1,0}},{C_{0,0,1}}} \right) = \sum\limits_{i = 1}^m {{r_i}{{\left( {{e_i}} \right)}^2}} $ | (8) |
式中, ri是各单元中心相对面心距离的倒数。对F求偏导,得到方程组,该方程组的解分别是速度分量u、v、w。
3) 人工粘性。使用人工密度法[5, 15]施加人工粘性,使用
| $ \tilde \rho = \rho - \mu \left[ {\frac{u}{q}{\rho _x}\Delta x + \frac{\upsilon }{q}{\rho _y}\Delta y + \frac{w}{q}{\rho _z}\Delta z} \right] $ | (9) |
式中, Δx、Δy和Δz分别是迎风单元中心到面心连线的向量分量的两倍,ρx、ρy和ρz是迎风单元中心处的密度梯度。m表达式为:
| $ \mu = \max \left[ {\begin{array}{*{20}{c}} 0&{(\mathit{M}{\mathit{a}^2} - \mathit{Ma}_{^c}^2)} \end{array}} \right]C $ | (10) |
Ma是迎风单元的马赫数。Mac是截断马赫数,常取0.95。C用来调整人工粘性大小,常取1到2之间。
4.1.3 GMRES隐式迭代求解隐式格式每步求解方程组:
| $ \mathit{Re}{\mathit{s}^{n + 1}} = 0 $ | (11) |
使用牛顿线性化的操作得到线性方程组:
| $ \frac{{\partial \mathit{Res}}}{{\partial \phi }}{\Delta ^n}\phi = - \mathit{Re}{\mathit{s}^n} $ | (12) |
本文使用结合ILU预调制方法[15]的GMRES算法解方程(12)。
4.2 欧拉方程及离散求解方法三维积分形式的欧拉方程为:
| $ \int {_{\mathit{\Omega }(\mathit{t})}} \frac{{\partial W}}{{\partial t}}{\rm{d}}V + \oint {_{\partial \mathit{\Omega }(\mathit{t})}} F\left( W \right){\rm{d \mathit{S} = 0}} $ | (13) |
其中:W=[ρ ρu ρv ρw ρe]T为守恒变量,其中ρ为流体密度,u、v和w为笛卡尔坐标系3个方向的绝对速度分量,e为单位质量总能;F(W)为对流通量。欧拉方程在空间上采用迎风格式有限体积离散,在时间方向上运用全隐式推进求解,离散方程采用GMRES格式迭代求解。
4.3 流场自适应的计算由于计算资源有限,为准确呈现流场特性,本文实施流场自适应。欧拉方法选择速度散度和旋度作为考察参数[9]。考虑到单元大小的影响,针对速度散度的参数的表达式为:
| $ {\tau _{di}} = \left| {\nabla \cdot \mathit{\boldsymbol{V}}} \right|l_i^{\frac{{r + 1}}{r}} $ | (14) |
速度散度▽· V 是使用4.1.2节中构建梯度的方法,用该单元网格面的速度插值求得的。li为该单元面积的算术平方根。r为调节参数,本文取2。计算所有单元τi的均方根作为基准,即:
| $ {\sigma _d} = \sqrt {\frac{{\sum {_{i = 1}^n\tau _{di}^2} }}{n}} $ | (15) |
对于旋度的考察参数,同样有
| $ {\tau _{ci}} = \left| {\nabla \times \mathit{\boldsymbol{V}}} \right|l_i^{\frac{{r + 1}}{r}},{\sigma _c} = \sqrt {\frac{{\sum {_{i = 1}^n\tau _{ci}^2} }}{n}} $ | (16) |
当τdi>σd或者τci>σc时,加密该单元;当τdi <
全速势和欧拉方法包含无黏假设只能计算诱导阻力。为计算黏性阻力系数,采用基于附面层理论和部件形状因子修正方法计算各部件的黏性阻力系数[3],通过叠加各部件的黏性阻力系数,获得全机的黏性阻力系数。
4.5 基于当地表面斜度法的面元法对于高超声速计算问题,可以采用欧拉方法,但对于特定的问题计算速度低且稳定性差。因此采用基于当地表面斜度理论的面元法计算气动力, 并采用三角形面元描述几何外形。面元按照撞击角分为迎风面和背风面,根据不同马赫数选取不同公式计算面元的压力系数。对于迎风面,Ma∞为1.5~3.8时,采用活塞-牛顿撞击理论[16];Ma∞为3.8~10时,采用修正牛顿撞击理论[17];Ma∞>10时,采用活塞-牛顿撞击理论。方法如下:
| $ {C_p} = \left\{ {\begin{array}{*{20}{l}} {{C_{p,\max }}(1 - D\;{{\cos }^G}\theta ),10 > M{a_\infty } > 1.5;}\\ {{C_{p,\max }}(\frac{{1 - B}}{{0.32M{a_\infty }}} + B\sin \theta )\sin \theta ,}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;M{a_\infty } \ge 10} \end{array}} \right. $ | (17) |
式中:
| $ {C_{\mathit{p}\max }} = \frac{2}{{\gamma Ma_\infty ^2}}\left\{ {{{\left[ {\frac{{{{(\gamma + 1)}^2}Ma_\infty ^2}}{{4\gamma Ma_\infty ^2 - 2(\gamma - 1)}}} \right]}^{\gamma /(\gamma - 1)}}\left[ {\frac{{1 - \gamma + 2\gamma Ma_\infty ^2}}{{\gamma + 1}}} \right] - 1} \right\} $ |
| $ D = \\ \left\{ \begin{array}{l} 1.570367 - 0.565058M{a_\infty } + 0.271167Ma_\infty ^2 - 0.0341656Ma_\infty ^3 + 0.002210593Ma_\infty ^4,\\ 3.8 \ge M{a_\infty } > 1.5\\ 1.0081057 - 0.0132323M{a_\infty } + 0.00164956Ma_\infty ^2 - 0.00006797Ma_\infty ^3,\\ 10 > M{a_\infty } > 3.8 \end{array} \right. $ |
| $ G = 2.6054749 - 0.465998M{a_\infty } + 0.09309305Ma_\infty ^2 - \\ 0.00817329Ma_\infty ^3 + 0.00026447Ma_\infty ^4 $ |
| $ B = \frac{2}{\pi }\arctan (\frac{{Ma_\infty ^2 + 6}}{{10}}) $ |
对背风面,则采用普朗特-迈耶膨胀波方法:
| $ {C_p} = - \frac{{\gamma + 1}}{2}{\theta ^2}\left\{ {\sqrt {1 + {{\left[ {\frac{4}{{(\gamma + 1)}}M{a_\infty }\theta } \right]}^2} - 1} } \right\} $ | (18) |
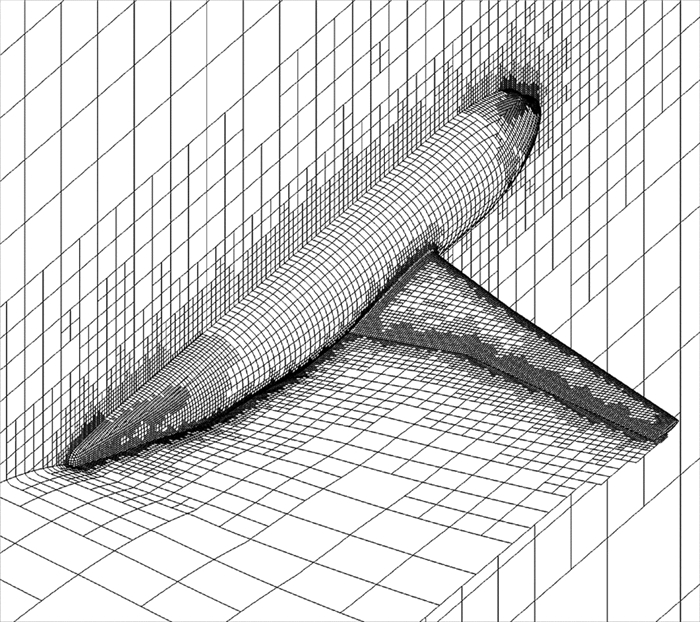
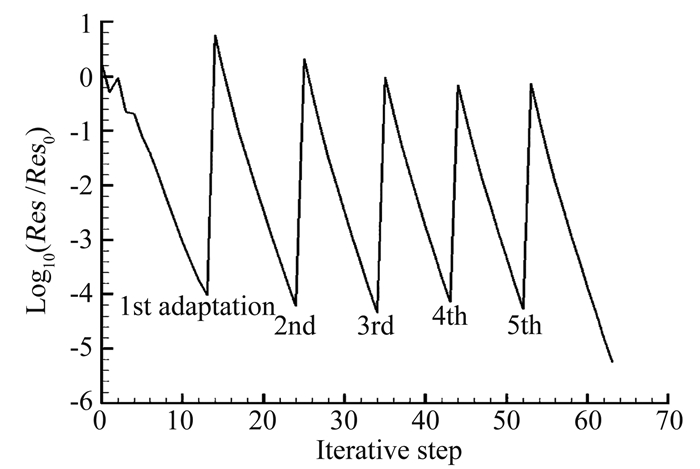
亚声速算例是针对DLR-F4进行数值分析,自由来流Ma∞=0.6,CL=0.5。4.3节中采用的流场自适应方法的效果在文献[18]已经得到了验证,并应用到了本文算例中。如图 3所示,计算网格进行了流场自适应,并且加密了流动参数变化剧烈的区域。图 4给出执行5次流场自适应后的收敛历程图。对同套网格,相比于课题组开发的欧拉方法求解器,该全速势方法计算时间缩短75%。本算例网格数为295 412个,不考虑流场自适应的情况下,在Intel Xeon E5-2630V2处理器上单核运行计算程序(下文所有算例均采用相同计算条件),仅需12个迭代步和240s的物理时间。
|
图 3 流场自适应后的计算网格 Figure 3 Computation grids after solution adaptation |
|
图 4 收敛历程图, Ma∞=0.6, CL=0.5 Figure 4 Residual convergence history, Ma∞=0.6, CL=0.5 |
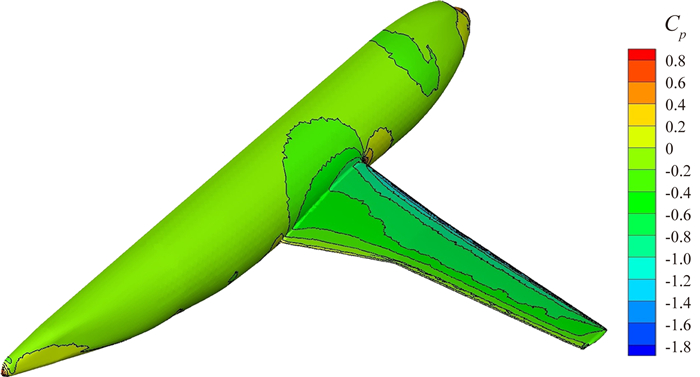
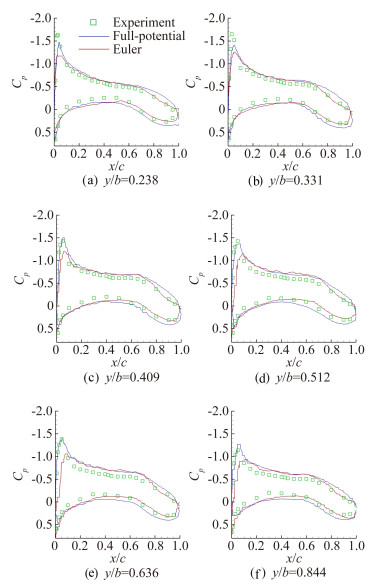
图 5给出了压力系数云图。图 6给出了本文全速势和欧拉方法于7个展向站位的压力系数和实验数据[19]的对比。可见前缘处全速势方法的精度更高,两种方法的结果都与实验数据相吻合。
|
图 5 压力系数云图, Ma∞=0.6, CL=0.5 Figure 5 Pressure coefficient contours, Ma∞=0.6, CL=0.5 |
|
图 6 DLR-F4亚声速压力系数对比图, Ma∞=0.6, CL=0.5 Figure 6 Comparison of pressure distributions of the subsonic flow over DLR-F4, Ma∞=0.6, CL=0.5 |
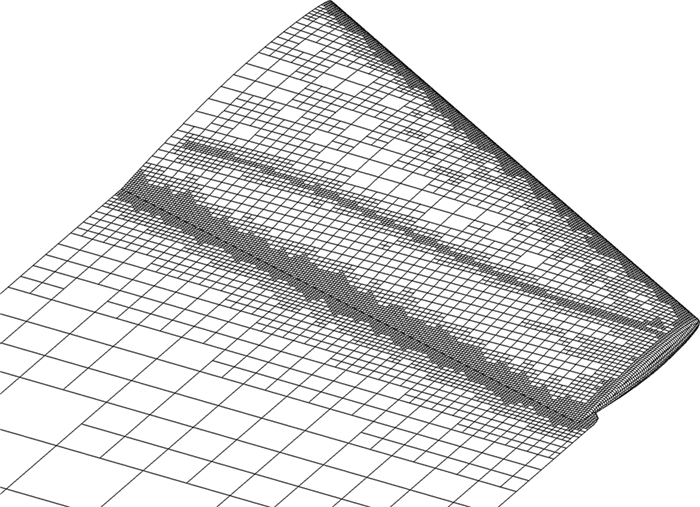
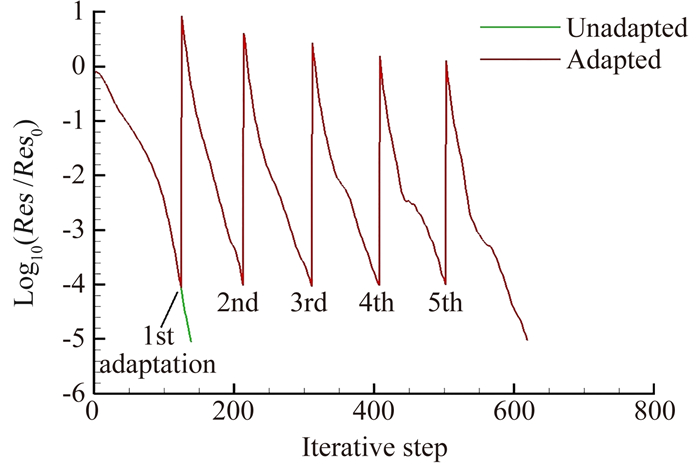
跨声速算例针对ONERA M6进行数值分析,自由来流Ma∞=0.839, α=3.06°。采用流场自适应来更精确地捕捉激波位置,如图 7所示。图 8给出了收敛历程图,可见每次流场自适应后流场保持了良好的收敛性。本算例网格数为151233个,不考虑流场自适应的情况下,计算时间约为15min。
|
图 7 ONERA M6自适应后的计算网格 Figure 7 Grids of ONERA M6 after solution adaptation |
|
图 8 收敛历程图, Ma∞=0.839, α=3.06° Figure 8 Residual convergence histories, Ma∞=0.839, α=3.06° |
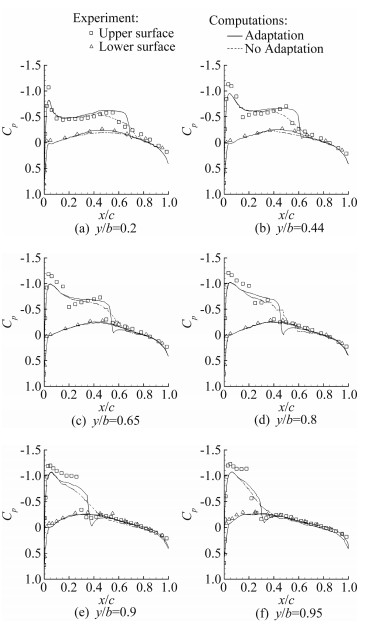
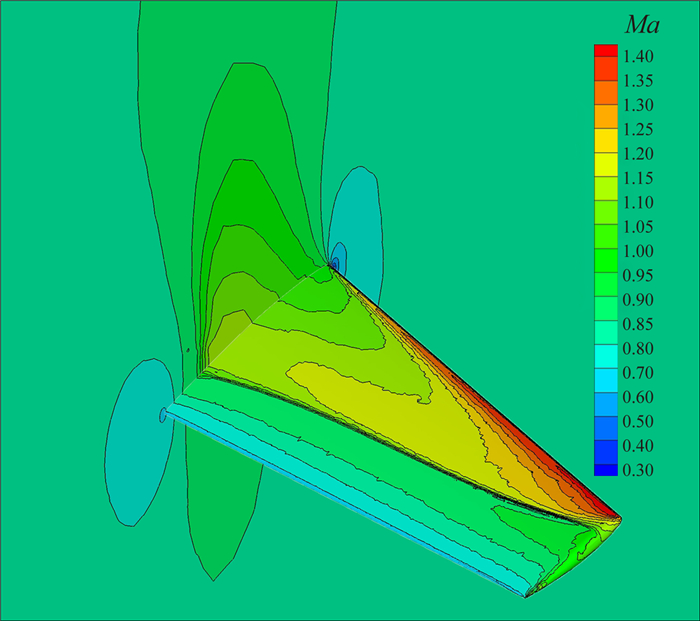
图 9展示了6个展向位置自适应前后压力系数的对比,可见流场自适应能显著提高计算精度。同时该图还给出了实验数据[20],可以看到计算结果和实验数据吻合的较好。图 10给出了机翼表面和对称面上的马赫数云图,本文的全速势方法成功捕捉了机翼上表面的Lambda型激波。
|
图 9 压力系数对比图, Ma∞=0.839, α=3.06° Figure 9 Pressure coefficient comparison, Ma∞=0.839, α=3.06° |
|
图 10 马赫数云图, Ma∞=0.839, α=3.06° Figure 10 Mach number contours, Ma∞=0.839, α=3.06° |
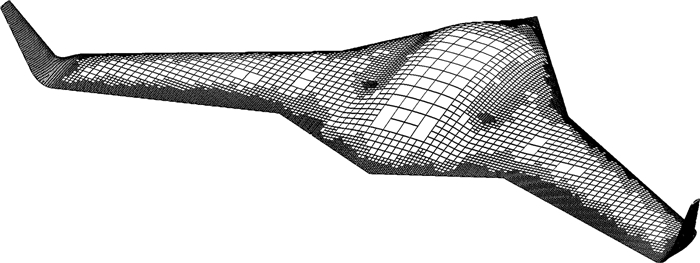
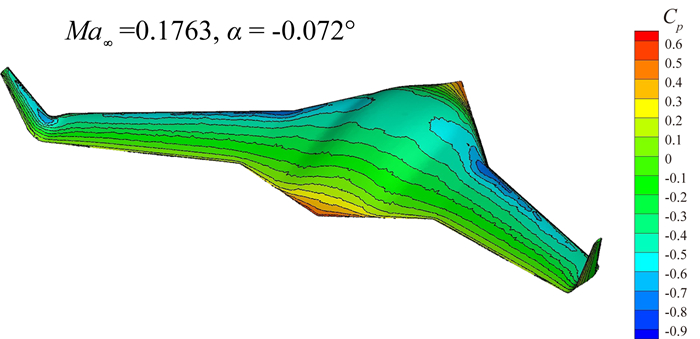
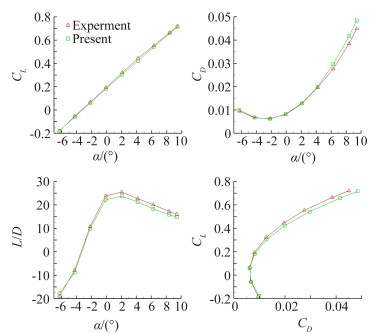
将该方法应用于翼身融合布局(BWB)无人机的亚声速计算仿真,Ma∞=0.1763, α=-6.28°~9.42°。实验数据来源于南京航空航天大学进行的低速风洞实验。图 11中展示该算例的计算网格,图 12给出了α=-0.072°时压力系数云图。图 13给出了升阻力特性曲线,可见计算结果和实验数据之间误差很小,比如升力系数最大误差小于4%。算例展示该方法在非常规布局飞行器研究中的应用价值。
|
图 11 BWB无人机的计算网格 Figure 11 Grids of BWB UAV |
|
图 12 BWB无人机的压力系数云图 Figure 12 Mach number contours of BWB UAV |
|
图 13 BWB无人机的升阻特性 Figure 13 Lift and drag coefficient of BWB UAV |
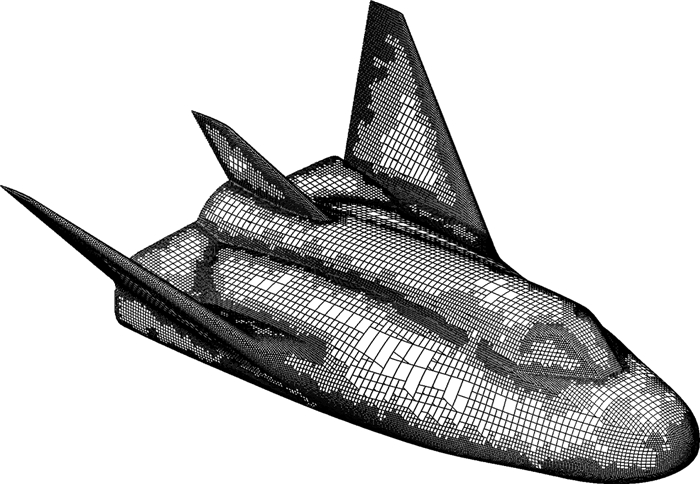
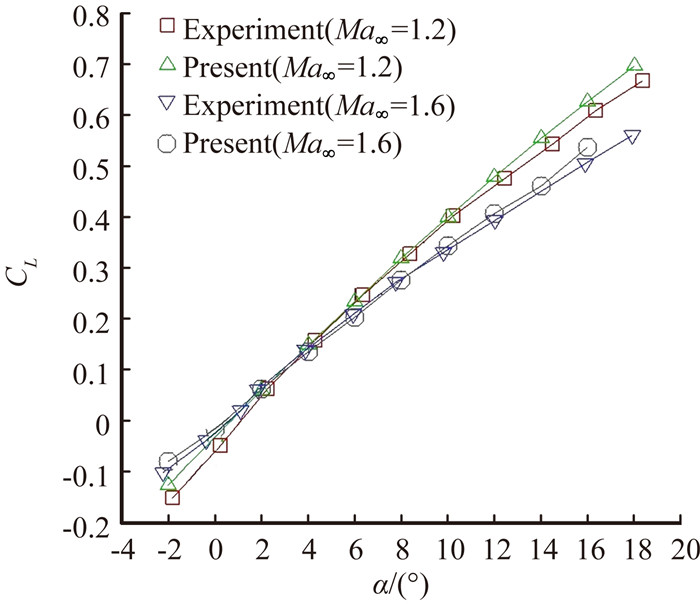
针对超声速流动问题,采用基于自适应直角网格的欧拉方法,相比于全速势方法,欧拉方法虽然计算速度相对较慢,但计算精度更高,尤其是对于激波较强的问题有更好的稳定性和精度。本节的算例来源于HL-20的风洞实验[21]。网格如图 14所示,可见本文的直角网格方法能够适应更加复杂的外形。图 15给出了自由来流Ma∞=1.2,α=0°时,流场自适应计算结果的马赫数云图。图 16给出了Ma∞=1.2和1.6时,不同迎角下升力系数计算结果和实验数据的对比,可见该方法和实验数据吻合度较高。网格数为412 730个,不考虑流场自适应的情况下,约需830迭代步和51min的物理时间。
|
图 14 HL-20的表面网格 Figure 14 Grids of HL-20 |

|
图 15 HL-20马赫数云图, Ma∞=1.2, α=0° Figure 15 Mach number contours of HL-20, Ma∞=1.2, α=0° |
|
图 16 HL-20升力系数对比 Figure 16 Comparison of lift coefficient of HL-20 |
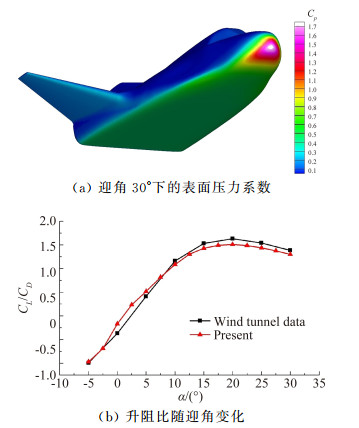
高超声速问题第一个算例是HL-20在Ma∞=6不同迎角下的升阻比的对比。图 17(a)为迎角30°工况下的表面压力系数分布;图 17(b)为升阻比随迎角的变化情况,可见计算结果与实验数据吻合良好,最大误差(发生在迎角2.5°)不超过7%。网格数为15320个,约需要20s的物理时间。
|
图 17 HL-20算例验证对比, Ma∞=6 Figure 17 Test case of HL-20, Ma∞=6 |
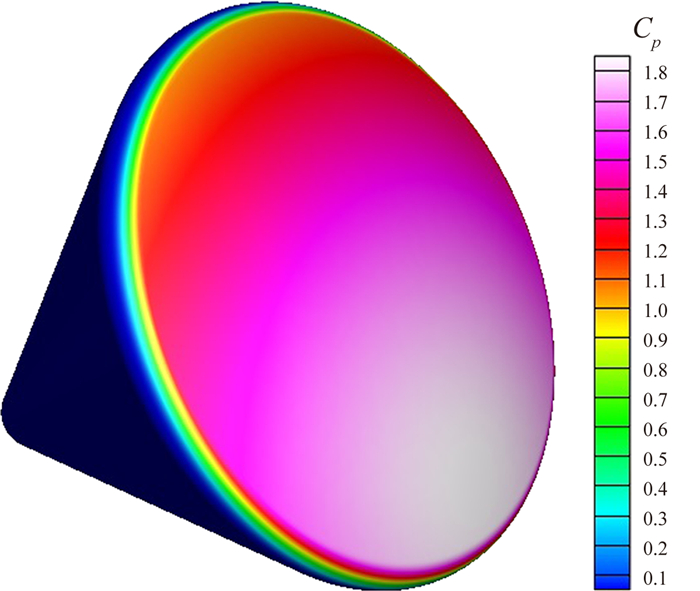
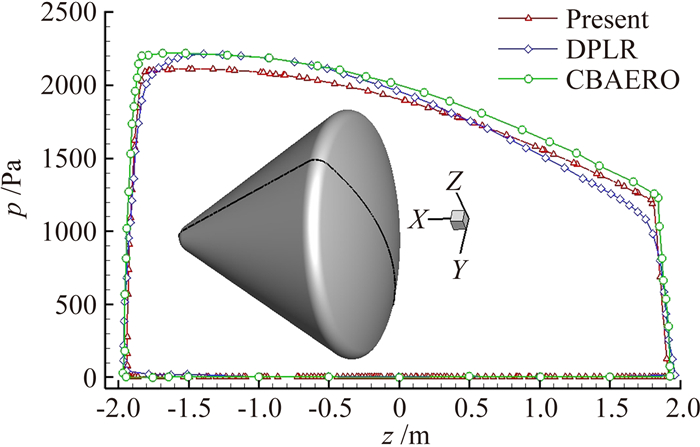
第二个算例是AS-202的数值分析[4, 22]。对比数据来源于CBAERO和DPLR对AS-202的仿真分析[4]。DPLR是高超声速流场精确求解CFD程序。在自由来流8.24km/s、Ma∞=28.6、迎角18.2°的工况下,图 18为返回舱的表面压力系数分布;图 19为本文方法的数据与CBAERO、DPLR仿真数据分析对比。从图 19可见,z < 0时,本文压强分布略小于CBAERO和DPLR;z>0时,本文方法的压强分布介于CBAERO和DPLR之间。
|
图 18 AS-202压力系数云图, Ma∞=28.6, α=18.2° Figure 18 Mach number contours of AS-202, Ma∞=28.6, α=18.2° |
|
图 19 AS-202中心线上的压强分布对比, Ma∞=28.6, α=18.2° Figure 19 Comparison of pressure on center line of AS-202, Ma∞=28.6, α=18.2° |
本文研究和开发了一种面向飞行器概念设计的全速域快速气动分析工具。若干不同速度域和不同构型的算例表明:
1) 由参数化几何建模程序、自适应直角网格方法程序、不同速度域的气动分析程序组成的气动分析工具,能快速地分析各种构型飞行器的气动特性,计算过程均可完全自动化。
2) 计算精度较好。基于自适应直角网格的全速势方程有限体积解法用于分析亚/跨声速气动问题,能够实现基于流场解的网格自适应,提高了激波捕捉的精度;基于自适应直角网格的欧拉方程有限体积解法用于分析有强激波流动问题,弥补了全速势方法的不足;当地表面斜度法的面元法用于高超声速声速问题,拓展了整套工具的适用范围,其计算速度非常快,计算精度较好。
综上所述,该工具能适用于全速域不同构型飞行器的气动特性分析,具有速度快、计算精度较好、所需计算资源少、自动化程度高的特点,适用于飞行器概念设计阶段的气动特性分析。
| [1] |
朱自强, 王晓璐, 吴宗成, 等. 民机设计中的多学科优化和数值模拟[J]. 航空学报, 2007, 28(1): 1-13. (  0) 0) |
| [2] |
De Weck O, Agte J, Sobieszczanski-Sobieski J, et al. State-of-the art and future trends in multidisciplinary design optimization[R]. AIAA 2007-1905, 2007.
(  0) 0) |
| [3] |
Bonner E, Clever W, Dunn K. Aerodynamic preliminary analysis system Ⅱ:Part Ⅰ-theory[R]. NASA CR-182076, 1991.
(  0) 0) |
| [4] |
Kinney D J, Garcia J A, Huynh L. Predicted convective and radiative aerothermodynamic environments for various reentry vehicles using CBAERO[C]//44th AIAA aerospace Sciences Meeting and Exhibit. Doi:10.2514/62006-659.
(  0) 0) |
| [5] |
Holst T L. Transonic flow computations using nonlinear potential methods[J]. Progress in Aerospace Sciences, 2000, 36(1): 1-61. DOI:10.1016/S0376-0421(99)00010-X (  0) 0) |
| [6] |
Bolsunovsky A L, Buzoverya N P, Karas O V, et al. An experience in aerodynamic design of transport aircraft[C]//28th International Congress of the Aeronautical Sciences. ICAS, 2012.
(  0) 0) |
| [7] |
Rubbert P E, Bussoletti J E, Johnson F T, et al. A new approach to the solution of boundary value problems involving complex configurations[J]. Computational Mechanics-advances & Trends Amd, 1986, 49-84. (  0) 0) |
| [8] |
Johnson F T, Tinoco E N, Yu N J. Thirty years of development and application of cfd at boeing commercial airplanes, seattle[J]. Computers and Fluids, 2005, 34(10): 1115-1151. DOI:10.1016/j.compfluid.2004.06.005 (  0) 0) |
| [9] |
De Zeeuw D L. A quadtree-based adaptively-refined Cartesian-grid algorithm for solution of the Euler equations[D]. Ann Arbor(MI):University of Michigan, 1993. http://www.tandfonline.com/doi/ref/10.1080/10407799808915064?scroll=top
(  0) 0) |
| [10] |
Aftosmis M J, Berger M J, Melton J E. Robust and efficient Cartesian mesh generation for component-based geometry[J]. AIAA Journal, 1998, 6(36): 952-960. (  0) 0) |
| [11] |
Hahn A. Vehicle sketch pad:A parametric geometry modeler for conceptual aircraft design[R]. AIAA 2010-657, 2010.
(  0) 0) |
| [12] |
Bonet J, Peraire J. An alternating digital tree(ADT)algorithm for 3D geometric searching and intersection problems[J]. International Journal for Numerical Methods in Engineering, 1991, 31(1): 1-17. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [13] |
Yang G, Causon D M, Ingram D M. Calculation of compressible flows about complex moving geometries using a three-dimensional Cartesian cut cell method[J]. International Journal for Numerical Methods in Fluids, 2000, 33(8): 1121-1151. DOI:10.1002/(ISSN)1097-0363 (  0) 0) |
| [14] |
Aftosmis M J, Berger M J, Adomavicius G. A parallel multilevel method for adaptively refined Cartesian grids with embedded boundaries[C]//38th Aerospace Sciences Meeting and Exhibit. Reno, Nevada, USA; 2000.
(  0) 0) |
| [15] |
Neel R E. Advances in computational fluid dynamics:Turbulent separated flows and transonic potential flows[D]. Blacksburg(VA):Virginia Polytechnic Institute and State University, 1997. http://scholar.lib.vt.edu/theses/browse/by_department/a.html
(  0) 0) |
| [16] |
张鲁明. 航天飞机空气动力学分析[M]. 国防工业出版社, 2009.
(  0) 0) |
| [17] |
Dejarnette F R, Ford C P, Young D E. Calculation of pressures on bodies at low angles of attack in supersonic flow[J]. Journal of Spacecraft and Rockets, 1980, 17(6): 529-536. DOI:10.2514/3.57770 (  0) 0) |
| [18] |
吕凡熹, 肖天航, 余雄庆. 基于自适应直角网格的二维全速势方程有限体积解法[J]. 计算力学学报, 2016, 33(03): 424-430. (  0) 0) |
| [19] |
Redeker G. DLR-F4 wing-body configuration[R]. Report No.:AGARD-AR-303, 1994.
(  0) 0) |
| [20] |
Schmitt V, Charpin F. Pressure distributions on the ONERA-M6-wing at transonic mach numbers, experimental data base for computer program assessment[R]. Paris:The Fluid Dynamics Panel Working Group 04, 1979.
(  0) 0) |
| [21] |
Ware G M, Cruz C I. Aerodynamic characteristics of the HL-20[J]. Journal of Spacecraft and Rockets, 1993, 30(5): 529-536. DOI:10.2514/3.25562 (  0) 0) |
| [22] |
Wright M J, Prabhu D K, Martinez E R. Analysis of apollo command module afterbody heating part Ⅰ:AS-202[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(1): 16-30. DOI:10.2514/1.15873 (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


