2. 中国空气动力研究与发展中心计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
为了减轻结构重量、提高飞行机动性,飞行器设计中倾向采用柔性的结构与材料,使得飞行器气动弹性效应日益明显,需要更加精确的气动弹性数值模拟工具用于飞行器的精细气动设计[1]。
此外,风洞模型的完全刚性假设在新型先进飞机设计中受到了挑战。越来越多的研究表明机翼在风洞气动载荷作用下的变形对模型气动特性存在明显的影响,而这种影响在增压试验中表现的更为显著[2]。例如波音的超声速运输机模型在美国兰利的NTF风洞开展高雷诺数风洞试验,翼梢扭转角可以达到-2.2°,由此造成不同速压下的巡航阻力系数差异最大接近50个阻力单位[3]。风洞模型静弹性变形对气动特性的影响已经引起了全世界研究者的关注与重视[4],高效高精度的静气动弹性计算程序逐渐成为研究这一问题的重要手段。
为了提高计算结果的可信度水平,国外广泛开展了气动弹性计算软件的验证与确认研究,其中影响范围较大的是AIAA发起的气动弹性预测研讨会AePW(Aeroelastic Prediction Workshop)[5],得到了世界范围内大量学者的积极响应。
近些年,随着计算机硬件技术的快速发展,国内高校与科研机构基于各自求解器开发了多种气动弹性数值计算平台[6-8],并广泛应用于解决工程实际问题,但静气动弹性数值计算程序精度验证方面的系统研究还比较少。
本文在课题组开发的流场计算软件TRIP上发展了一套高效的静气动弹性计算模块,下文将简要介绍计算模块的架构、组成、流程和采用的数值方法。然后通过2个算例对计算模块的精度进行验证。
1 静气动弹性计算模块架构图 1给出了TRIP软件静气动弹性计算模块的总体架构,该模块包含四个主要功能单元:气动数值计算、结构静变形计算、耦合界面数据插值以及动态网格方法,四个主要功能单元采用弱耦合方式串联在一起,如图 1所示。

|
图 1 静气动 Figure 1 Sketch of static computational aeroelasticity module |
图 1的左侧给出了气动载荷和结构位移的传递路线。首先CFD计算出气动载荷,利用界面数据插值将气动载荷传递给CSM,CSM利用气动输入载荷计算得到结构的位移,通过界面数据插值再将结构位移传递给流场,并利用动态网格技术生成流场物面变形后的新网格,CFD再计算新网格下的流场。如此反复迭代,直至载荷和位移均达到收敛。图 1的右侧给出了每个功能单元采用的主要计算方法,下节将对这些计算方法进行更加详细的介绍。
2 数值计算方法 2.1 流场计算方法流场解算器采用课题组开发多年的亚跨超流场解算软件TRIP。TRIP软件通过有限体积法离散求解欧拉(Euler)和雷诺平均方程(RANS),方程对流项离散采用二阶MUSCL型的Roe通量差分分裂格式,粘性项离散采用二阶中心差分格式,湍流模型采用工程常用的单方程SA模型[9]与两方程SST模型[10],计算加速方面采用多重网格和基于MPI信息传递的并行计算。课题组针对TRIP已经开展了大量的算例验证与测试,软件的精度和可信度得到了广泛的认可[11-12]。
2.2 结构静变形计算方法结构静变形计算采用柔度矩阵、模态叠加和有限元数值求解三种方法。
柔度矩阵方法中,结构网格点的位移通过下式计算得到:
| ${\mathit{\boldsymbol{u}}_{\rm{s}}} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{f}}_{\rm{s}}}$ | (1) |
式中,us为结构网格点的位移矩阵,C为结构的柔度矩阵,fs为结构网格点上的输入载荷。本文中结构柔度矩阵C通过有限元模型施加单位载荷的位移响应组装得到。
模态叠加法中,结构网格点的位移通过下式计算得到[13]:
| ${\mathit{\boldsymbol{u}}_{\rm{s}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{s}}}\mathit{\boldsymbol{q}}$ | (2) |
式中,us含义同式(1),Φs为结构的广义模态矩阵,通过结构模态分析得到,q为系统的广义位移矢量。对于结构静变形有:
| $\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{u}}_{\rm{s}}} = {\mathit{\boldsymbol{f}}_{\rm{s}}}$ | (3) |
式中,K为结构的刚度矩阵,fs含义同式(1),式(2) 代入式(3),可以得到:
| $\mathit{\boldsymbol{q}} = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{s}}^{\rm{T}}{\mathit{\boldsymbol{f}}_{\rm{s}}}$ | (4) |
式中:
| $\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{s}}^{\rm{T}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{s}}} = {\rm{diag}}\left( {\omega _1^2, \ldots ,\omega _n^2} \right)$ | (5) |
式中,Ω为结构模态刚度矩阵,是一个对角阵,对角线各元素为广义模态圆频率的平方。式(4) 代入式(2) 即可求解得到结构网格点的位移:
| ${\mathit{\boldsymbol{u}}_{\rm{s}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{s}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{s}}^{\rm{T}}\mathit{\boldsymbol{f}}$ | (6) |
有限元数值求解采用了自主编写的一套结构静变形求解程序,在方法上借鉴了商业软件Nastran的数据格式和众多开源程序的设计架构。
2.3 耦合界面数据传递气动/结构之间的数据传递可以通过一个矩阵进行描述,比如对于位移变量可以表示为:
| ${\mathit{\boldsymbol{u}}_{\rm{a}}}{\rm{ = }}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{u}}_{\rm{s}}}$ | (7) |
式中,u为网格点位移矢量,下标a表示气动,下标s表示结构,H为转换矩阵。为了满足传递过程中的能量守恒,有虚功原理可以得到:
| ${\mathit{\boldsymbol{f}}_{\rm{s}}} = {\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{f}}_{\rm{a}}}$ | (8) |
式中,f为网格点上的载荷。
本文静气动弹性计算模块采用RBF、TPS和IPS三种方法构建传递矩阵H。一般形式的径向基函数插值可以表示为[14]:
| $f\left( \mathit{\boldsymbol{x}} \right) = {\beta _0} + \sum\limits_{j = 1}^m {{\beta _j}{x_j}} + \sum\limits_{i = 1}^N {{\gamma _i}\varphi \left( {\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right\|} \right)} $ | (9) |
式中,f(x)为被插函数,x为插值点位置坐标,xi为插值基点的位置坐标,xj(j=1, …, m)为位置坐标的分量,‖ x -xi‖表示两点之间的距离,N为插值基点的数量,m为描述问题的维数,二维m为2,三维m为3,βi(i=0, …, m)、γi(i=1, …, N)为插值系数,φ为径向基函数。
利用RBF方法得到的传递矩阵H可以表示为:
| $\mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{H}}_1}{\mathit{\boldsymbol{H}}_2}$ | (10) |
其中:
| ${\mathit{\boldsymbol{H}}_1}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 1&{{x_{{\rm{a}},1,1}}}& \cdots &{{x_{{\rm{a}},1,\mathit{m}}}}&{{\varphi _{{x_{{\rm{a}},1}}\;{x_{{\rm{s,}}1}}}}}& \cdots &{{\varphi _{{x_{{\rm{a}},1}}\;{x_{{\rm{s,}}\mathit{N}}}}}}\\ 1&{{x_{{\rm{a}},2,1}}}& \cdots &{{x_{{\rm{a}},2,\mathit{m}}}}&{{\varphi _{{x_{{\rm{a}},2}}\;{x_{{\rm{s,}}1}}}}}& \cdots &{{\varphi _{{x_{{\rm{a}},2}}\;{x_{{\rm{s,}}\mathit{N}}}}}}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 1&{{x_{{\rm{a}},\mathit{M},1}}}& \cdots &{{x_{{\rm{a}},1,\mathit{m}}}}&{{\varphi _{{x_{{\rm{a}},\mathit{M}}}\;{x_{{\rm{s,}}1}}}}}& \cdots &{{\varphi _{{x_{{\rm{a}},\mathit{M}}}\;{x_{{\rm{s,}}\mathit{N}}}}}} \end{array}} \right]$ | (11) |
| ${\mathit{\boldsymbol{H}}_2} = {\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{{\mathit{\boldsymbol{P}}^{\rm{T}}}}\\ \mathit{\boldsymbol{P}}&\mathit{\boldsymbol{R}} \end{array}} \right]^{ - 1}}\left[ \begin{array}{l} {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array} \right]$ | (12) |
| $\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} 1&{{x_{{\rm{s,}}1,1}}}& \cdots &{{x_{{\rm{s,}}1,\mathit{m}}}}\\ 1&{{x_{{\rm{s,2}},1}}}& \cdots &{{x_{{\rm{s,2}},\mathit{m}}}}\\ \vdots & \vdots & \ddots & \vdots \\ 1&{{x_{{\rm{s,}}\mathit{N},1}}}& \cdots &{{x_{{\rm{s,}}\mathit{N},\mathit{m}}}} \end{array}} \right]$ | (13) |
| $\mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{\varphi _{{x_{{\rm{s}},1}}\;{x_{{\rm{s,1}}}}}}}& \cdots &{{\varphi _{{x_{{\rm{s}},1}}\;{x_{{\rm{s,}}\mathit{N}}}}}}\\ \vdots & \ddots & \vdots \\ {{\varphi _{{x_{{\rm{s}},\mathit{N}}}\;{x_{{\rm{s,1}}}}}}}& \cdots &{{\varphi _{{x_{{\rm{s}},\mathit{N}}}\;{x_{{\rm{s,}}\mathit{N}}}}}} \end{array}} \right]$ | (14) |
式(11) 中的M为气动网格点的数目,式(12) 中右侧的0为(m+1)×N的零矩阵,I为N×N的单位矩阵。
不同的基函数φ可以得到不同的传递矩阵H,TPS和IPS是RBF插值的一种特殊形式,对应不同的基函数类型,基函数的选取可以参考文献[14]。
2.4 动态网格生成本文动态网格生成采用网格变形的思路,可以避免引起新的数值离散误差。目前计算模块主要采用面向结构网格的RBF+TFI方法,针对一些特殊问题,也采用RBF+Delaunay和RBF+HBGM的网格变形方法,有关这些方法可以参考文献[15-16]。
3 静气动弹性计算模块精度验证本节将首先通过一个大展弦比机翼的变形结果分析三种不同结构静变形计算方法的差异,然后利用两个风洞模型的试验数据结果对静气动弹性计算模块精度进行验证。下文如不作特殊说明,流场计算中湍流模拟采用两方程SST模型,耦合数据传递采用TPS方法,动态网格变形采用RBF+TFI方法。
3.1 大展弦比机翼变形结果分析本小节将分析三种不同结构静变形求解方法结果的差异,图 2给出了采用的大展弦比机翼的外形、网格和有限元模型。其中有限元模型采用不同厚度的壳单元构建,因此耦合数据传递采用IPS方法。

|
图 2 大展弦比机翼外形、流场网格和有限元模型 Figure 2 Shape, grid and FEM model of high respect-ratio wing |
图 3给出了三种不同方法计算得到的大展弦比机翼变形结果,图中Mode n表示采用结构前n阶模态位移的变形计算结果。

|
图 3 大展弦比机翼变形结果 Figure 3 Deformation results of high respect-ratio wing |
图 3可以看出:柔度矩阵方法与有限元分析结构一致性很好,模态叠加方法的变形结果与选取的模态有关。但随着模态数量的增加,模态方法的结果与前两种方法的结果也很快趋向一致。另一方面,不同模态对弯曲变形和扭转变形的贡献不同,对于弯曲变形,前2阶的结构模态贡献了主要的变形,而对于扭转变形,后续模态仍然有着明显的贡献。因此,在选择结构模态计算结构静变形时,应当首先开展结构模态对静变形计算结果的影响分析。如不作特殊说明,本文后续的算例中均采用柔度矩阵方法计算结构静变形。
3.2 DLR-F6模型静气动弹性模拟DLR-F6是德国宇航院设计的一类现代民用运输机标模,在多座风洞开展了不同类型的风洞试验,具有丰富的试验数据,有关DLR-F6模型的详细可以参考文献[17]。本文采用DLR-F6的翼身组合体构型开展精度验证,图 4给出了该构型的外形、网格拓扑和有限元模型。

|
图 4 DLR-F6外形、网格拓扑与有限元模型 Figure 4 Shape, grid topology and FEM model of DLR-F6 |
流场计算Ma数为0.75,基于平均气动弦长的雷诺数Re为3.0×106,模型迎角为-3°~1.5°,来流速压q与模型材料弹性模量E的比值q/E为2.0×10-7。图 5给出了该计算参数条件下DLR-F6翼身组合体模型机翼变形展向分布结果。图中Test表示在NASA的NTF风洞利用光学方法测量的机翼变形,TAU为DLR的流场解算程序。

|
图 5 DLR-F6模型变形结果 Figure 5 Deformation results of DLR-F6 model |
可以看出:不同升力系数下,试验Test、TAU和本文Present得到的弯曲变形结果在变形分布和量值上都比较一致,表明本文静气动弹性计算模块采用了正确的算法流程且具有较好的弯曲变形预测精度。由于DLR-F6是实体金属模型,来流的速压并不大,因此由气动载荷引起的机翼最大弯曲变形并不明显,约为6.5mm(半翼展为585.6mm)。
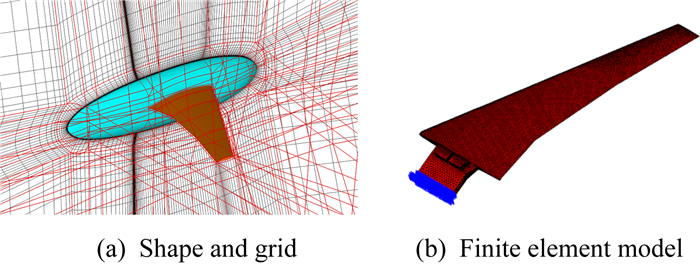
3.3 HIRENASD模型静气动弹性模拟HIRENASD是亚琛工大设计的一类典型运输机机翼外形,在欧洲跨声速风洞ETW开展了大量试验,有关HIRENASD模型的详细参数可以参考文献[18]。为了消除壁面边界层对机翼流场的影响,风洞中给HIRENASD机翼模型安装了一个假机身,本文采用包含假机身的外形开展静气动弹性模拟。图 6给出了HIRENASD机翼模型的外形、网格拓扑和有限元模型。其中流场计算网格从气动弹性预测会议AePW的官网上下载得到,为ICEM软件生成的多块对接网格,如图 6(a);有限元的固支约束添加在机翼与天平连接的端面上,如图 6(b)。
|
图 6 HIRENASD外形、网格拓扑和有限元模型 Figure 6 Shape, grid topology and FEM model of HIRENASD |
流场计算的Ma数为0.80,基于平均气动弦长的雷诺数Re为1.4×107,模型迎角α为3°,来流速压q与模型材料弹性模量E的比值q/E为4.7×10-7。
图 7给出了该参数条件下的机翼弯曲变形展向分布结果,可以看出,试验Test、TAU和本文Present得到的机翼变形结果十分吻合。

|
图 7 HIRENASD机翼弯曲位移展向分布 Figure 7 Spanwise bending of HIRENASD wing |
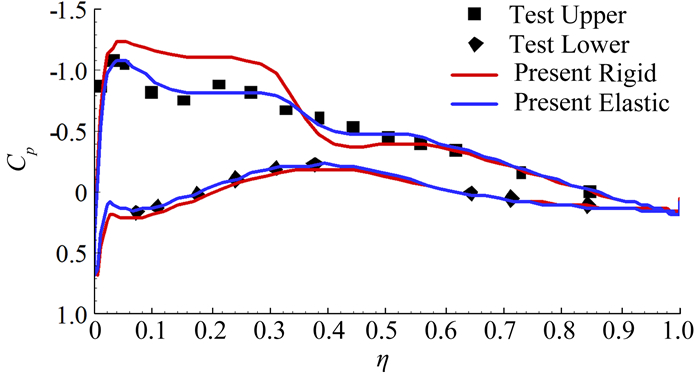
图 8给出了HIRENASD机翼展向相对位置η等于0.95时的翼剖面压力系数分布,可以看出,采用刚性外形,计算的压力系数分布与试验结果之间存在显著的差异,而采用静气动弹性耦合计算得到的压力系数分布与试验结果十分吻合,进一步验证了本文静气动弹性计算模块的精度。
|
图 8 HIRENASD翼剖面压力系数分布(η=0.95) Figure 8 Pressure coefficient distribution of HIRENASD wing section (η=0.95) |
本文在TRIP软件基础发展了静气动弹性计算模块,并通过算例对计算结果的精度进行了验证,说明该计算模块具有较好的静气动弹性预测精度。同时,计算结果表明风洞模型结构静变形对压力系数分布有着明显影响,应当得到试验数据使用单位的重视。
致谢:本文得到了课题组张玉伦、洪俊武、王光学、张书俊、李伟和杨小川等人的帮助,在此表示感谢。
| [1] |
Mouton S, Sant Y, Lyonnet M. Predication of the aerodynamic effect of model deformation during transonic wind tunnel tests[J]. International Journal of Engineering Systems Modelling and Simulation, 2013, 5(1-3): 44-56. (  0) 0) |
| [2] |
孙岩, 张征宇, 邓小刚, 等. 风洞模型静弹性变形对气动力影响研究[J]. 空气动力学学报, 2013, 31(3): 294-300. (  0) 0) |
| [3] |
Owens L R, Wahls R A, Rivers S M. Off-design Reynolds number effects for a supersonic transport[J]. Journal of Aricraft, 2005, 42(6): 1427-441. DOI:10.2514/1.10433 (  0) 0) |
| [4] |
Levy D W, Laflin K R, Tinoco E N, et al. Summary of data from the fifth computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2014, 51(4): 1194-1213. DOI:10.2514/1.C032389 (  0) 0) |
| [5] |
Heeg J, Chwalowski P, Florance J P, et al. Overview of the aeroelastic predication workshop[R]. AIAA 2013-0783, 2013.
(  0) 0) |
| [6] |
杨超, 王立波, 谢长川, 等. 大变形飞机配平与飞行载荷分析方法[J]. 中国科学(E辑:技术科学), 2012, 42(10): 1137-1147. (  0) 0) |
| [7] |
徐敏, 邱滋华, 裴曦. 基于CFD/CSD/CAA耦合的声气动弹性仿真技术在壁板颤振中的应用[J]. 强度与环境, 2013, 40(5): 16-24. (  0) 0) |
| [8] |
黄炜, 陆志良, 唐迪, 等. 基于多点约束的大展弦比机翼静气动弹性计算[J]. 北京航空航天大学学报, 2014, 40(12): 1666-1671. (  0) 0) |
| [9] |
Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992.
(  0) 0) |
| [10] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 (  0) 0) |
| [11] |
王运涛, 王光学, 张玉伦. DPWⅢ机翼和翼身组合体构型数值模拟[J]. 空气动力学学报, 2011, 29(3): 264-269. (  0) 0) |
| [12] |
王运涛, 张书俊, 孟德虹. DPW4翼/身/平尾组合体的数值模拟[J]. 空气动力学学报, 2013, 31(6): 739-744. (  0) 0) |
| [13] |
Ritter M. Static and forced motion aeroelastic simulations ofthe HIRENASD wind tunnel model[R]. AIAA 2012-1633, 2012.
(  0) 0) |
| [14] |
Rendall T C S, Allen C B. Unified fluid-structure interpolation and mesh motion using radial basis functions[J]. International Journal for Numerical Methods in Engineering, 2008, 74: 1519-1559. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [15] |
孙岩, 邓小刚, 王运涛, 等. RBF_TFI结构动网格技术在风洞静气动弹性修正中的应用[J]. 工程力学, 2014, 31(10): 228-233. (  0) 0) |
| [16] |
孙岩, 邓小刚, 王光学, 等. 基于径向基函数改进的Delaunay图映射动网格方法[J]. 航空学报, 2014, 35(3): 727-735. (  0) 0) |
| [17] |
Burner A W, Goad W K, Massey E A, et al. Wind deformation measurements of the DLR-F6 transport configuration in the national transonic facility[R]. AIAA 2008-6921, 2008.
(  0) 0) |
| [18] |
Ritter M, Hassan D. Assesment of the ONERA/DLR numerical aeroelastics predication capabilities on the HIRENASD configuration[R]. IFASD-2011-109, 2011.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35


