2. 中国人民解放军 96833 部队, 湖南 怀化 418000;
3. 沈阳飞机设计研究所, 辽宁 沈阳 110035
2. The 96833 troops of the Chinese People's Liberation Army, Huaihua 418000, China;
3. Shenyang Aircraft Design and Research Institute, Shenyang 110035, China
按照流体微团是否在垂直于主流的运动方向上受到限制,湍流可分为自由湍流和壁湍流,后者的湍流特征主要集中在固壁边界层内,壁面剪切决定了其与自由湍流之间存在本质区别。壁湍流广泛存在于自然界和工程界中流体和固体壁面发生相对运动的场合。近半个世纪以来对于壁湍流的研究主要基于光滑壁面假设,如对数区及标度律[1-3]、近壁区自维持循环[4-5]、拉格朗日标量输运[6]、湍流结构系综理论[7-8]等。光滑壁面假设壁面的粗糙度(以粗糙高度的均方根来衡量)相对于壁湍流的粘性尺度(ν/uτ,uτ为摩擦速度,ν为运动粘性系数)是小量,通常认为:内尺度无量纲的粗糙特征高度k+=kuτ/ν < 4~5是水力光滑条件(文中上标+均表示用内尺度无量纲)。对于常见的工程流动(超声速流动除外)来说,壁湍流的粘性尺度在2~20μm的范围内,经过机械精加工的固壁工作面的粗糙度在0.05~25μm的水平,通常满足水力光滑条件[9]。光滑壁面不考虑壁面粗糙度对粘性底层以上各流层(y+>5) 的影响,减少了实验研究的不可控因素,因此被涉及到湍流机理的基础研究所普遍采用。目前,绝大多数RANS(雷诺平均N-S方程)方法中的湍流模型和LES(大涡模拟)方法中的亚格子模型,都是基于光滑壁面假设。
然而,自然界也存在很多粗糙度对固壁工作面的影响不能被忽略的情况,如:大气表面层(其边界层厚度约在500m量级)流经森林或城市建筑群[10],鲨鱼表皮存在规则齿状凸起[11]等。工程界中很多原本水力光滑的表面,在经过一段时间的运营后会降级为粗糙壁面,如:船舶壳体被海水侵蚀,风机/涡轮叶片被昆虫/油污附着[12],输水/油管道被泥沙/油污沉积,高超声速飞行器表面被气动热烧蚀等。这会带来摩擦阻力的增加,造成壁面散热和传质效率偏离设计状态,增加设备的运营成本或缩短全寿命使用周期。此外,对汽车、飞行器等运载工具而言,即使其工作表面光滑,但实际存在各种尺度的几何缺陷,如:铆钉、检修舱盖、传感器罩、舱门缝隙等,仍会破坏固壁表面光滑平顺条件,这些离散的壁面缺陷,如果特征尺度小于当地边界层厚度,也可被抽象为离散粗糙单元。由此可见,粗糙在自然界和工程领域都较为普遍,研究壁面粗糙对于湍流边界层的影响,能够为认清并解决这些自然和工程问题提供指导性意见。
对粗糙壁湍流的研究起源于粗糙管流水头损失实验[13-15],此后的研究多针对单一小尺度粗糙连续分布在壁面上的情况,如:砂纸、线网壁面等,由此发展起以速度亏损律、壁面相似律为代表的粗糙壁湍流经典理论[16]。然而,对中高雷诺数光滑壁湍流的最新研究表明,湍流边界层不同流层中不同尺度的拟序结构之间存在相互作用[17-20],即:不同流层的湍流结构之间是相互影响、彼此依赖的,这给粗糙壁湍流经典理论的上述观点带来了挑战。粗糙元对不同流层湍流结构的影响以及壁面相似律的适用性已经成为壁湍流研究领域一个热点问题。本文总结近年来国内外在粗糙壁湍流研究中所取得的重要成果,并进一步讨论今后可能的研究方向。
1 光滑壁湍流拟序结构在概述粗糙壁湍流的研究成果前,先简单介绍光滑壁湍流中的主要结构, 以便后文阐明粗糙壁湍流的最近发现。光滑壁湍流中已经发现的典型拟序结构分别是:近壁条带结构[21-23]和流向涡[24]、发卡涡或马蹄涡结构[25-28]以及近期发现的大尺度运动(LSMs)和超大尺度运动(VLSMs)[29-31]。
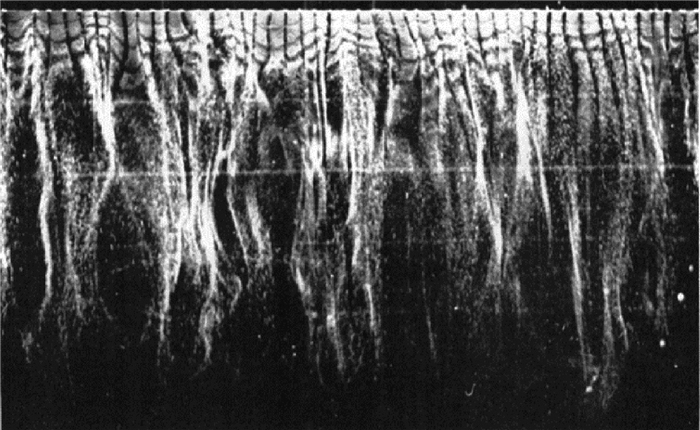
图 1给出光滑壁湍流中近壁区的典型条带结构[21],当y+ < 30时,低速条带呈现出沿流向拉长(流向可达1000壁面粘性单位以上)、沿展向准周期变化的特征,其展向平均间距(范围在80~120个壁面粘性单位之间)几乎不随雷诺数变化,但随离开壁面的距离有增大的趋势[32]。在近壁区与低速条带有密切空间位置关系的是准流向涡结构,流向涡两侧分别为高速和低速流体,在流向涡上/下洗作用下形成的上抛和下扫过程是近壁区雷诺切应力产生的根源[32-33],同时,条带和流向涡是近壁区自维持循环得以实现的关键拟序结构[4, 34-35]。
马蹄涡(发卡涡)结构最早是由Theodorsen提出的一种概念模型[26],其特征是两条沿流向拉长的涡腿与抬起的沿展向呈弓形的涡头相连,后期在湍流边界层的直接数值模拟[36-37]和实验[38]中均被观测到。潘翀[39]等、杨越[6]等和何国胜[40-41]等近期的拉格朗日观测给出了转捩边界层中近壁流体卷起形成马蹄涡的细节,潘翀等[42]用拉格朗日方法刻画了低雷诺数湍流边界层中马蹄涡形成马蹄涡包的过程,如图 2所示。
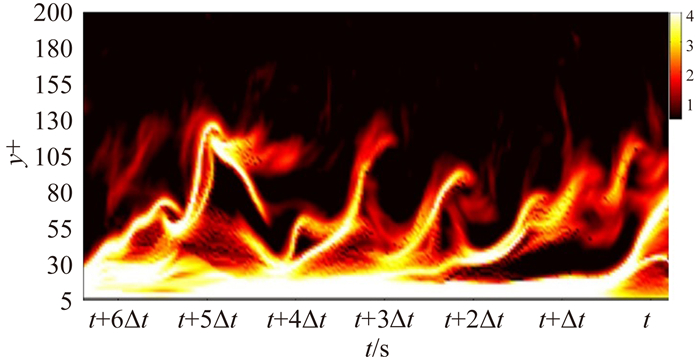
|
图 2 利用李雅普诺夫指数积分得到的壁湍流马蹄涡包结构[42] Figure 2 Horseshoe vortex packets in the wall-bounded turbulence identified by Finite-Time Lyapunov Exponents method[42] |
Adrian等[28, 38]的研究表明,近壁区的马蹄涡主要以涡包的形式存在,如图 3所示。涡包内含有沿流向排列的多个发卡涡,其具有大致相同的对流速度,在涡腿之间协同诱导产生大尺度的低流向动量区,即为LSMs,其流向尺度约为2δ~3δ(δ为边界层厚度)。随着雷诺数的提高,大尺度结构可延伸至对数区和尾迹区[29-31, 43],以超长且弯折的低流向动量区为主要形态, 这种结构在内流中通常被称为超大尺度结构(VLSMs),在外流中则被称为超结构。VLSMs的流向尺度可达边界层厚度的10~15倍,郑晓静等[44]在大气边界层(Reτ=uτδ/ν=3×106)中同样发现了超大尺度运动。VLSMs和LSMs运动对湍动能和雷诺应力生成有重要贡献,Balakumar[45]发现:40%~65%的湍动能和30%~50%的雷诺切应力来源于流向波长(λx/δ)>3的长模态,Ganapathisubramani等[46]也发现对数区的涡包结构对近壁区雷诺切应力的贡献很大。
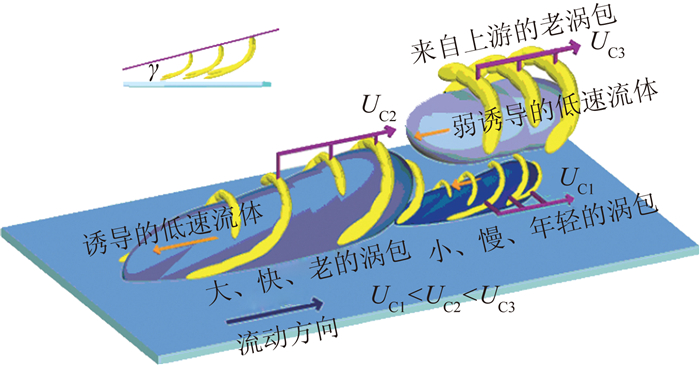
|
图 3 Adrian等[28]提出的马蹄涡包模型 Figure 3 Conceptual scenario of horseshoe vortex packets proposed by Adrian[28] |
内外区的大/小尺度结构存在明确的相互作用。如,在DNS和实验中均发现内区中存在大尺度运动的印迹[47-48],Hutchins[49]发现远壁区的大尺度结构对近壁运动具有明显的调制作用。黄永祥[50]发现在槽道湍流中,随雷诺数增大,大尺度结构对壁面平均摩擦应力的贡献增加。Deck等[51]最近的分区离散大涡模拟(DES)研究表明,内外层的湍流结构间存在强耦合,表现为外区大尺度结构的强度受到平均剪切和近壁区小尺度的影响,同时对内区小尺度结构在能谱和雷诺应力上进行调制。许春晓等[52-53]分析了抽吸气/旋转运动对中等雷诺数槽道湍流的抑制机制,发现压力-应力和压力-扩散项首先突破垂向应力输运的平衡并最终导致了湍流强度的全局性的抑制。
2 粗糙壁湍流上一节简要介绍了光滑壁湍流的四种典型拟序结构。在中高雷诺数下,四种拟序结构存在相互作用,这既丰富了壁湍流的复杂性,也给实际研究带来了进一步的难度。本节将在此基础上,从三个方面总结国内外学者在粗糙壁湍流研究中所取得的最新成果,分别为:壁面相似律、壁面离散粗糙的绕流结构及其对湍流边界层原有结构的影响。
2.1 壁面相似律如前所述,速度亏损律和壁面相似律是粗糙壁湍流经典理论的最主要成就[16],速度亏损律基于如下实验发现:壁面上存在的小尺度连续粗糙将整体拉低平均流向速度型U+(y+),内尺度无量纲公式为:
| $ {U^ + } = \frac{1}{\kappa }\ln \left( {{y^ + }} \right) + A - \Delta {U^ + } $ | (1) |
其中,κ和A分别是卡门常数和积分常数,ΔU+称为粗糙函数。一般认为ΔU+与粗糙所引起的当地摩擦系数的增量相关[54]。建立ΔU+与粗糙的特征尺度的函数关系,曾是很长一段时间内的研究重点,如著名的Nikuradse公式[15]:
| $ \Delta {U^ + } = \frac{1}{\kappa }\ln \left( {k_s^ + } \right) + A - 8.5 $ | (2) |
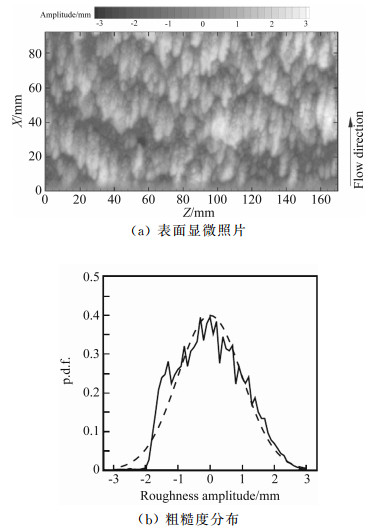
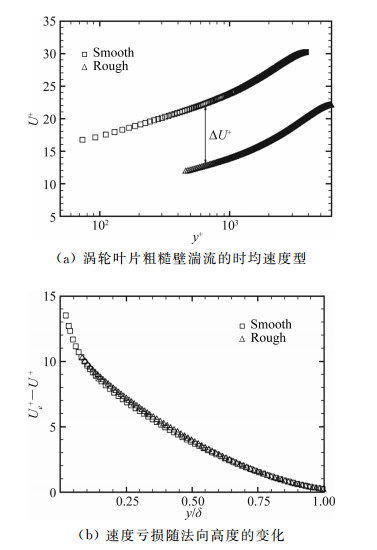
其中ks称为等效砂砾高度。Wu等[55]研究涡轮叶片经过一段时间后演变成的粗糙对湍流边界层的影响,图 4所示为粗糙的表面形状及粗糙度的概率密度分布,图 5为利用PIV实验得到的时均速度剖面,在此实验中,粗糙函数ΔU+=8.2,无量纲的等效砂砾高度ks+=115。
|
图 4 涡轮叶片在工作过一段时间后演变成的粗糙形态[55] Figure 4 Roughness replicated from an actual turbine blade damaged by deposition of foreign materials[55] |
|
图 5 利用PIV实验得到的时均速度剖面[55], Ue为无穷远处来流速度. Figure 5 Mean velocity profiles and velocity defect scalings obtained by PIV experiments[55], Ue is the free stream velocity. |
研究发现,工程界的大部分小尺度粗糙,其特征高度k与等效砂砾高度ks成正比,称其为k型粗糙。2000年以前,针对粗糙的几何形状、密集度等对k/ks具体数值的影响进行了大量测量[56-58]。研究表明,当ks+>70后,k/ks将不再受到粗糙几何形状和密集度等因素的明显影响,称为完全粗糙,此时的粗糙雷诺数ks+与粗糙函数呈对数线性关系,即满足Nikuradse公式。粗糙雷诺数ks+ < 40~50时的粗糙称为过渡粗糙,此时近壁面流动受到粘性和压力项的共同作用。
与k型粗糙相对应的是d型粗糙,此时ks不再依赖于k,Perry等[59]认为ks依赖于δ,即ks/δ为常数,但学术界对此尚有争议[9]。d型粗糙对湍流研究有着特殊的意义:传统壁湍流存在内外两个不同的特征尺度(粘性尺度和边界层厚度),而d型粗糙控制的壁湍流只依赖于一个外尺度。近20年对二维方槽(一种典型的d型粗糙)的研究表明,槽内的回流泡与槽外的流动隔绝,因此方槽起到改变壁面零点的作用,其特征高度并不决定ks和ΔU+。
壁面相似律是速度亏损律的自然延伸,主要基于对高雷诺数下外区湍流特性独立于壁面条件的认识[60]。壁面相似律指出:在高雷诺数条件下,粗糙的影响仅限于粗糙底层之内,它的作用只是决定壁面摩擦速度、水力零点、粗糙底层以内的流动以及边界层厚度,而不影响到外区湍流统计特性和流动结构,这一观点被早期的研究所证实[9, 16, 55, 61]。所谓粗糙底层是指距离壁面2k~5k的区域,在粗糙底层以内,流动的特征尺度主要决定于粗糙的特征尺寸。然而也有研究表明,壁面粗糙对湍流的影响可能并不仅局限于粗糙底层以内,而是会延伸到外区,导致壁面相似律失效[62-64]。Jimenez[9]指出只有保证足够高的粗糙雷诺数(ks+>100) 和足够大的尺度分离(δ/k)>50时,壁面相似律才有可能成立,此时雷诺数Reτ应至少大于4000。Flack[65]采用等效砂砾高度作为衡量标准并指出壁面相似律成立条件是(δ/ks)>40。
为了进一步丰富壁面相似律的适用条件,Marusic等[66]近期利用热线测量了光滑和砂纸状粗糙壁面的湍流统计量,粗糙雷诺数范围20 < ks+ < 155,包括过渡粗糙和完全粗糙,雷诺数范围2020 < Reτ < 21 430,他们在时均速度和脉动速度曲线中均发现了明显的对数区,且其斜率不随粗糙雷诺数变化,与光滑壁湍流对数区斜率一致。在外区,时均速度亏损和速度偏度曲线与光滑壁湍流具有较好一致性,验证了壁面相似律的适用性。而对于速度的二阶统计距,当雷诺数Reτ>14 000或者完全粗糙壁情况下,光滑/粗糙壁湍流的曲线吻合较好。
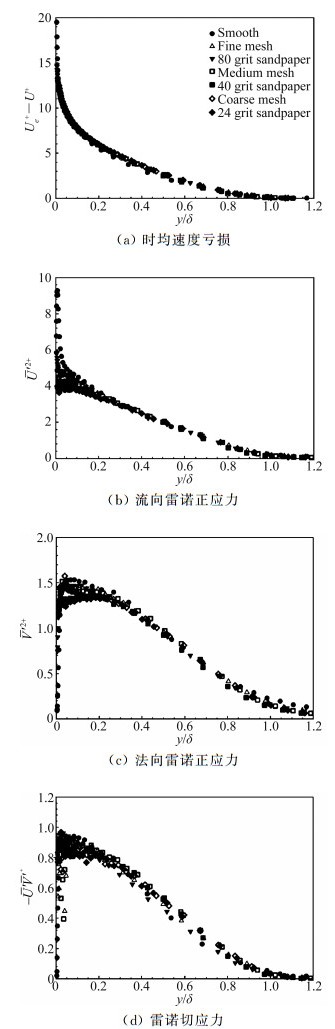
类似的结论也在Flack和Schultz的研究[67-70]中得到,他们利用实验的方法对不同形状的粗糙进行了大量的研究,涉及三维粗糙(砂纸[65]、网状[67]、正方体[68]等)和二维粗糙(细长条状粗糙[69]),结果表明只要保证足够高的雷诺数和足够大的尺度分离,粗糙对湍流统计量的影响仅局限于粗糙底层以内,外区统计量与同雷诺数下光滑壁湍流相一致(图 6所示),进一步的谱分析和两点相关结果表明外区流动结构与光滑壁湍流同样具有较高的相似性[67]。
|
图 6 不同形状的粗糙壁湍流与光滑壁湍流统计量沿法向分布对比[70] Figure 6 Turbulence statistics comparisons between smooth and rough wall[70] |
王晋军等[71-72]较早的开展了粗糙壁面明槽湍流的研究,使用激光多普勒测速仪测量了湍流统计特性的分布规律,发现增加粗糙高度将使近壁区湍流均匀化的现象,提出了满足自相似性的判据。陶建军等[73]从理论上探讨了圆管表面粗糙度对流动转捩的影响,并针对雷诺数从800至1×106的粗糙管实验给出摩阻因子的一般形式。车得福等[74]研究了二维V型沟槽对湍流统计特性的影响,发现沟槽的密集度是一个重要的控制参数;在特定情况下,ΔU+不满足传统的亏损律,沟槽的影响将延伸至外区,改变扫掠事件对雷诺切应力和单点高阶统计矩的贡献率。
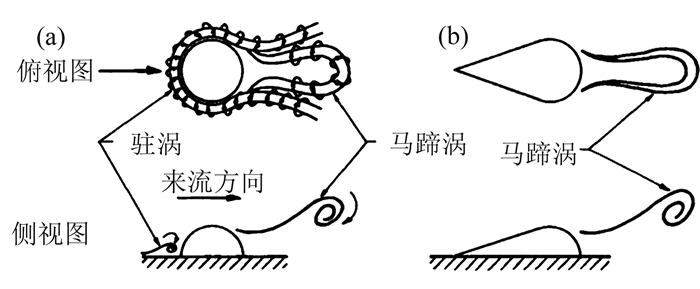
2.2 壁面粗糙单元的绕流结构探究壁面粗糙对于湍流边界层的影响,需要弄清楚置于壁面的粗糙单元的绕流结构。Acarlar和Smith[75]利用氢气泡显示的方法详细对比观察了半球形和半泪滴形粗糙的绕流结构,他们发现粗糙后方的尾迹结构主要包括两部分:近壁面的低速条带结构、粗糙上方的马蹄涡及其诱导的二次流动结构,流动示意图如图 7所示。当基于粗糙高度和当地流速的特征雷诺数Rek>120(Rek=ukk/ν,uk为相同雷诺数下光滑壁湍流中同一位置上的流速),马蹄涡周期性的从粗糙后方的剪切层中脱落。
|
图 7 (a) 半球形粗糙绕流结构;(b)半泪滴形粗糙绕流结构[75] Figure 7 (a) Flow structures around hemisphere; (b) flow structures around half teardrop[75] |
从转捩/湍流控制的角度来说,通常不希望粗糙尾迹中包含此类周期性脱落的涡结构,从而促进近壁区以小尺度拟序结构为核心的湍动能自维持过程,因此研究者们所选用的壁面粗糙一般工作于亚临界范围内,即尾迹中只含有稳定的低速结构,从而起到抑制近壁区湍流横向脉动的作用。Klebanoff等[76]发现:对于高径比为1的三维离散粗糙,临界雷诺数Rek=500~700,Erigin等[77]发现:当高径比小于1后,离散粗糙的临界雷诺数下降到300附近,并被后来的DNS所证实[78]。
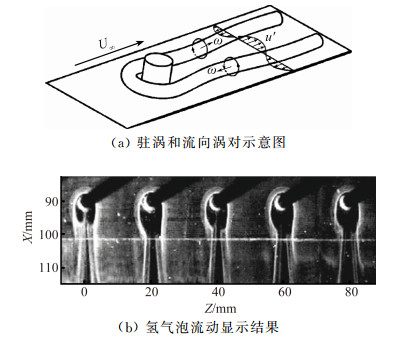
王晋军等[79]通过氢气泡流动显示研究了单个小半球和多个小半球对于边界层发展的影响,对于单个半球粗糙,发现在驻涡和粗糙之间有一个明显的间隔,位于x/r=-1.75(r为半球半径)之内的流体不会卷入驻涡,粗糙上方脱落的发卡涡的高度随着流速的增加而减少。潘翀等[80]研究了圆柱状离散粗糙颗粒在亚临界/过临界状态下的绕流结构,流动显示结果表明粗糙颗粒在其上游引入逆压梯度,在逆压梯度的作用下边界层内的流体在粗糙颗粒的上游发生分离,并因此卷起一个或多个展向驻涡,驻涡在粗颗粒两侧向下游弯折,形成一对反向旋转的流向涡,示意图及流动显示结果如图 8所示,进一步的研究发现对应实验状态下的粗糙临界雷诺数Rek介于339和443之间。
2.3 粗糙壁湍流统计规律和流动结构上一节介绍了流体流过粗糙所产生的流动拓扑结构,本节阐明这些流动结构与湍流原有拟序结构发生相互干扰/作用后,将对原有的湍流统计特性和流动结构产生哪些影响。
在粗糙对近壁流动影响方面,Grass等[81-82]用氢气泡显示的方法发现粗糙的存在增加了喷射/扫掠事件,但抑制了近壁区的流向涡结构。Pearson等[83]研究了砂砾对低雷诺数壁湍流的影响,发现当流体流过一段砂纸时,近壁区条带结构被破坏,体现在流向相关尺度缩短,展向相关尺度增大;而在砂纸的下游,条带结构会逐渐恢复至光滑壁湍流的水平。Krogstad等[84]利用热线测量了网状粗糙壁湍流的三速度分量,结果表明:在x-y平面,流向速度两点相关ρuu的倾斜角大约为38°,而在光滑壁湍流中此角度大约为10°~15°[85],且与光滑壁湍流相比,流向尺度大幅度减小而展向尺度变化不大。Bhaganagar等[86-87]的DNS研究表明,近壁区条带的平均间距受到粗糙的显著影响,且近壁区的瞬时涡结构相比于光滑壁湍流更为复杂。
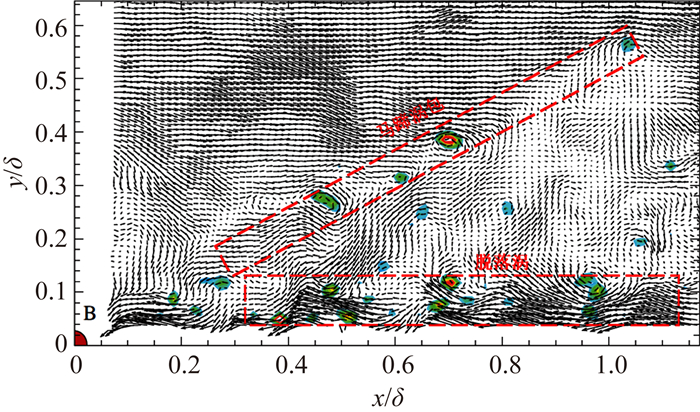
Guala等[88]采用二维PIV研究了离散半球状粗糙对壁湍流的影响,拍摄平面为x-y平面,他们在离散粗糙壁面的下游流场中发现了马蹄涡包和脱落涡结构,如图 9红色虚线框所示,B为粗糙位置。两点相关结果表明,对比光滑壁湍流,其流向尺度及马蹄涡包倾角均有所减小,其原因可能是粗糙表面脱落的涡结构破坏了原有湍流结构,增加了近壁区喷射事件的发生频率。
|
图 9 离散半球状粗糙壁湍流中瞬时流场矢量图,图中伪彩色区域为瞬时展向漩涡强度场[88] Figure 9 Instantaneous flow field downstream of hemisphere. Iso-contours of swirling strength are superimposed on the velocity vector field[88] |
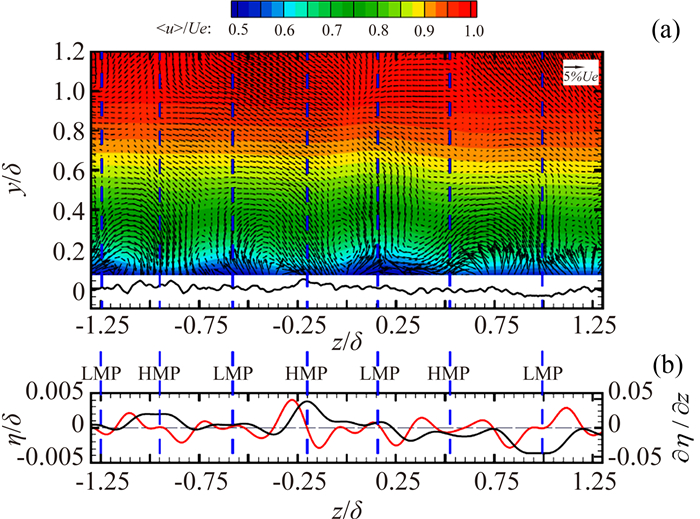
Wu等[55, 89]实验研究了涡轮叶片经过一段时间后演变形成的实际粗糙对湍流边界层外区结构的影响(粗糙形状如图 4所示),他们发现在粗糙底层以上,两点相关的流向和展向尺度均与光滑壁湍流差异不大,进一步的本征正交分解(POD)表明,远壁区的大尺度结构易受壁面粗糙的影响,而小尺度结构所受影响不明显。在最近的实验研究中,Wu等[90]发现时均流动沿展向呈现高/低动量区(High/Low momentum flow pathways, HMP/LMP)交替分布特性,并在其交界处伴随有较强的旋涡(如图 10所示),进一步的分析表明高低动量区出现的位置正好分别对应粗糙外形轮廓凸起和凹陷的展向位置。
|
图 10 (a) y-z平面时均流向速度云图,叠加垂向和展向速度矢量,蓝色虚线表示HMP/LMP的位置,下方曲线勾勒出粗糙外形轮廓图;(b)滤波后的剖面形状(黑色实线)和其展向梯度(红色实线),η表示粗糙高度[90] Figure 10 (a) The mean velocity field (counters u; vector v and w) with the spanwise roughness profile shown below the field; (b) The low-pass-filtered spanwise roughness profile (black line) and its spanwise gradient (red line)[90] |
离散粗糙引入的绕流结构,在合适的条件下也能通过与湍流原有流动结构发生相互作用而抑制近壁区湍流脉动。如,王希麟等[91-92]研究了展向不同间距和不同粒径的离散粗糙颗粒对近壁湍流拟序结构的影响,得出的结论是:合理选择粗糙间距和高度能够实现近壁湍流控制及减阻等。王晋军等[93]在对沟槽面湍流边界层近壁区拟序结构的研究中发现:沟槽限制了流体的横向流动,增强了流动的稳定性,并揭示了沟槽面减阻的机理。Zhang X[94]等研究了圆柱状离散粗糙颗粒对壁湍流近壁区流场的影响,发现粗糙尾迹能够主控近壁条带的展向间距和sinuous不稳定性,控制效果可以延伸至250个壁面单位的下游,但是,目前仍然缺乏对控制机理的深入认识。
3 研究现状总结总结20世纪50年代以来国外对于粗糙壁湍流的研究工作,大部分都是围绕壁面相似律展开,通过与光滑壁湍流对比,分析粗糙对湍流边界层内、外区流动结构/统计特性的影响,如果粗糙的影响范围仅限于粗糙底层之内,则认为壁面相似律成立,反之失效。但最新壁湍流研究表明:中高雷诺数下壁湍流不同流层中不同尺度的拟序结构之间存在相互作用,如大尺度运动对小尺度结构的调制作用[20],这给粗糙壁湍流的上述经典理论带来了挑战,粗糙的存在是否会改变不同尺度结构间相互作用的形式以及如何改变,将是今后的研究方向。
国内对于粗糙壁湍流的研究起步稍晚,目前还没有形成一个完整的理论体系,所以仍需要不断借鉴国外的优秀研究成果,同时在其基础上思索创新的可能,可以从粗糙外形(如分形粗糙)、数据处理手段(如动力学模态分解)以及实验技术(如体式PIV)等方面加以考虑。研究不同形式的粗糙单元的绕流结构及其对壁湍流流场统计特性和流动结构的影响,将有助于进一步丰富对壁湍流拟序结构尺度间相互作用的认识,厘清内外区在湍动能/雷诺应力生成、标量输运等方面的不同地位和作用。
| [1] |
Barenblatt G I, et al. Structure of the zero-pressure-gradient turbulent boundary layer[C]//Proceedings of the National Academy of Sciences of the United States of America, 1997, 94(15):7817-7819.
(  0) 0) |
| [2] |
Jiang N, Wang Y C. An experimental research on the extended self-similarity in wall-bounded turbulence[J]. Journal of Experimental Mechanics, 2002, 17(1): 28-34. (in Chinese) 姜楠, 王玉春. 壁湍流扩展的自相似标度律的实验研究[J]. 实验力学, 2002, 17(1): 28-34. (  0) 0) |
| [3] |
Zhang K, Li W P. PIV experimental research of the scaling low in wall turbulence[J]. Journal of Experimental Mechanics, 2008, 23(6): 549-556. (in Chinese) 张珂, 李万平. 壁面湍流标度律的PIV实验研究[J]. 实验力学, 2008, 23(6): 549-556. (  0) 0) |
| [4] |
Hamilton J M, Kim J, Waleffe F. Regeneration mechanisms of near-wall turbulence structures[J]. Journal of Fluid Mechanics, 1995, 287(3): 317-348. (  0) 0) |
| [5] |
Yacine Bengana. Self-sustaining process of minimal attached eddies in turbulent channel flow[J]. Journal of Fluid Mechanics, 2016, 795: 708. DOI:10.1017/jfm.2016.226 (  0) 0) |
| [6] |
Zhao Y, Yang Y, Chen S. Evolution of material surfaces in the temporal transition in channel flow[J]. Journal of Fluid Mechanics, 2016, 793: 840-876. DOI:10.1017/jfm.2016.152 (  0) 0) |
| [7] |
She Z S, et al. A multi-state description of roughness effects in turbulent pipe flow[J]. New Journal of Physics, 2012, 14(9): 093054. DOI:10.1088/1367-2630/14/9/093054 (  0) 0) |
| [8] |
Chen X, Hussain F, She Z S. Predictions of canonical wall-bounded turbulent flows via a modified k-ω equation[J]. Journal of Turbulence, 2017, 18(1). (  0) 0) |
| [9] |
Jiménez J. Turbulent flows over rough walls[J]. Annual Review of Fluid Mechanics, 2004, 36(1): 173-96. DOI:10.1146/annurev.fluid.36.050802.122103 (  0) 0) |
| [10] |
Zhu W L, Yang Q S. Large eddy simulation of flow around a low-rise buliding immersed in turbulent boundary layer[J]. Journal of Building Structures, 2010, 31(10): 41-47. (in Chinese) 朱伟亮, 杨庆山. 湍流边界层中低矮建筑绕流大涡模拟[J]. 建筑结构学报, 2010, 31(10): 41-47. (  0) 0) |
| [11] |
Wen L, Weaver J C, Lauder G V. Biomimetic shark skin:design, fabrication and hydrodynamic function[J]. Journal of Experimental Biology, 2014, 217(10): 1656-1666. DOI:10.1242/jeb.097097 (  0) 0) |
| [12] |
Bons J P, et al. The many faces of turbine surface roughness[J]. Journal of Turbomachinery-Transactions of the Asme, 2001, 123(4): 739-748. DOI:10.1115/1.1400115 (  0) 0) |
| [13] |
Hagen G. Vber den einfluss der temperatur auf die bewegung des wassers in r hren[J]. Math. Abh. Akad. Wiss. Berlin, 1854, 17-98. (  0) 0) |
| [14] |
Darcy H. Recherches expérimentales relatives au mouvement de l'eau dans les tuyaux[M]. 1857, Paris:Mallet-Bachelier. 268.
(  0) 0) |
| [15] |
Nikuradse J. Str mungsgesetze in rauhen rohren forschhft[J]. Ver. Dt. Ing, 1933, 361. (  0) 0) |
| [16] |
Raupach M R, Antonia R A, Rajagopalan S. Rough-wall turbulent boundary layers[J]. Applied Mechanics Reviews, 1991, 44(1). (  0) 0) |
| [17] |
Marusic I, et al. Wall-bounded turbulent flows at high Reynolds numbers:Recent advances and key issues[J]. Physics of Fluids, 2010, 22(6). (  0) 0) |
| [18] |
Smits A, McKeon B, Marusic I. High-Reynolds number wall turbulence[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 353-375. DOI:10.1146/annurev-fluid-122109-160753 (  0) 0) |
| [19] |
Duvvuri S, McKeon B J. Triadic scale interactions in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2015, 767. (  0) 0) |
| [20] |
Marusic I, Mathis R, Hutchins N. Predictive model for wall-bounded turbulent flow[J]. Science, 2010, 329(5988): 193. DOI:10.1126/science.1188765 (  0) 0) |
| [21] |
Kline S, et al. The structure of turbulent boundary layers[J]. Journal of Fluid Mechanics, 1967, 30(04): 741-773. DOI:10.1017/S0022112067001740 (  0) 0) |
| [22] |
Schoppa W, Hussain F. Coherent structure generation in near-wall turbulence[J]. Journal of Fluid Mechanics, 2002, 453(4): 57-108. (  0) 0) |
| [23] |
Smith C R, Metzler S P. The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1983, 129(-1): 27-54. DOI:10.1017/S0022112083000634 (  0) 0) |
| [24] |
Hussain F, Schoppa W, Kim J. Coherent structures near the wall in a turbulent channel flow[J]. Journal of Fluid Mechanics, 1997, 332(01): 185-214. (  0) 0) |
| [25] |
Lian Q X. Experimetnal study on the coherent structures in turbulent boundary layer[J]. Advances in Mechanics, 2006, 36(3): 373-388. (in Chinese) 连祺祥. 湍流边界层拟序结构的实验研究[J]. 力学进展, 2006, 36(3): 373-388. DOI:10.6052/1000-0992-2006-3-J2005-043 (  0) 0) |
| [26] |
Theodorsen T. Mechanism of turbulence[C]//Proceedings of the Second Midwestern Conference on Fluid Mechanics. 1952. Ohio State University.
(  0) 0) |
| [27] |
Xu C X. Coherent structures and drag-reduction mechanism in wall-bounded turbulence[J]. Advances in Mechanics, 2015, 45(6). (in Chinese) 许春晓. 壁湍流相干结构和减阻控制机理研究进展[J]. 力学进展, 2015, 45(6). (  0) 0) |
| [28] |
Adrian R J. Hairpin vortex organization in wall turbulencea[J]. Physics of Fluids(1994-present), 2007, 19(4): 041301. (  0) 0) |
| [29] |
Hutchins N, Marusic I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2007, 579(579): 1-28. (  0) 0) |
| [30] |
Kim K C. Very large-scale motion in the outer layer[J]. Physics of Fluids, 1999, 11(2): 417-422. DOI:10.1063/1.869889 (  0) 0) |
| [31] |
Balakumar B J, Adrian R J. Large-and very-large-scale motions in channel and boundary-layer flows[J]. Philosophical Transactions Mathematical Physical & Engineering Sciences, 2007, 365(1852): 665-681. (  0) 0) |
| [32] |
Kim J, Moin P, Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. Journal of Fluid Mechanics, 1987, 177(177): 133-166. (  0) 0) |
| [33] |
Landahl M T. A note on an algebraic instability of inviscid parallel shear flows[J]. Journal of Fluid Mechanics, 1980, 98(98): 243-251. (  0) 0) |
| [34] |
Waleffe F. On a self-sustaining process in shear flows[J]. Physics of Fluids, 1997, 9(4): 883-900. DOI:10.1063/1.869185 (  0) 0) |
| [35] |
Pan C, Wang J J. Progress in bypass transition induced by free-stream disturbance[J]. Advances in Mechanics, 2011, 41(6): 668-685. (in Chinese) 潘翀, 王晋军. 自由来流扰动引起的旁路转捩研究进展[J]. 力学进展, 2011, 41(6): 668-685. DOI:10.6052/1000-0992-2011-6-lxjzJ2011-070 (  0) 0) |
| [36] |
Robinson S K. Coherent motions in the turbulent boundary layer[J]. Annual Review of Fluid Mechanics, 1991, 23(1): 601-639. DOI:10.1146/annurev.fl.23.010191.003125 (  0) 0) |
| [37] |
Wu X, Moin P. Forest of hairpins in a low-Reynolds-number zero-pressure-gradient flat-plate boundary layer[J]. Physics of Fluids, 2009, 21(9): 297. (  0) 0) |
| [38] |
Adrian R J, Meinhart C D, Tomkins C D. Vortex organization in the outer region of the turbulent boundary layer[J]. Journal of Fluid Mechanics, 2000, 422(422): 1-54. (  0) 0) |
| [39] |
Pan C, et al. Coherent structures in bypass transition induced by a cylinder wake[J]. Journal of Fluid Mechanics, 2008, 603(603): 367-389. (  0) 0) |
| [40] |
He G S. Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer[J]. Journal of Fluid Mechanics, 2016, 792: 274-306. DOI:10.1017/jfm.2016.81 (  0) 0) |
| [41] |
He G S, et al. Vortex dynamics for flow over a circular cylinder in proximity to a wall[J]. Journal of Fluid Mechanics, 2017, 812: 698-720. DOI:10.1017/jfm.2016.812 (  0) 0) |
| [42] |
Pan C, Wang J J, Zhang C. Identification of Lagrangian coherent structures in the turbulent boundary layer[J]. Science China Physics, Mechanics & Astronomy, 2009, 52(2): 248-257. (  0) 0) |
| [43] |
M, G, H. Se, Rj A. Large-scale and very-large-scale motions in turbulent pipe flow[J]. Journal of Fluid Mechanics, 2006, 554(-1):521-542.
(  0) 0) |
| [44] |
Zheng Xiaojing. Very large scale motions in the atmospheric surface layer:a field investigation[J]. Journal of Fluid Mechanics, 2016, 802: 464-489. DOI:10.1017/jfm.2016.439 (  0) 0) |
| [45] |
Balakumar B J, Adrian R J. Large-and very-large-scale motions in channel and boundary-layer flows[J]. Philosophical Transactions of the Royal Society a-Mathematical Physical and Engineering Sciences, 2007, 365(1852): 665-681. DOI:10.1098/rsta.2006.1940 (  0) 0) |
| [46] |
Ganapathisubramani B, Longmire E K, Marusic I. Characteristics of vortex packets in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2003, 478: 35-46. (  0) 0) |
| [47] |
Hoyas S, Jimenez J. Scaling of the velocity fluctuations in turbulent channels up to Re-tau=2003[J]. Physics of Fluids, 2006, 18(1). (  0) 0) |
| [48] |
Hutchins N, Marusic I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2007, 579: 1-28. DOI:10.1017/S0022112006003946 (  0) 0) |
| [49] |
Hutchins N, Marusic I. Large-scale influences in near-wall turbulence[J]. Philosophical Transactions of the Royal Society A Mathematical Physical and Engineering Sciences, 2007, 365(1852): 647-664. DOI:10.1098/rsta.2006.1942 (  0) 0) |
| [50] |
Hwang Y. Near-wall turbulent fluctuations in the absence of wide outer motions[J]. Journal of Fluid Mechanics, 2013, 723: 264-288. DOI:10.1017/jfm.2013.133 (  0) 0) |
| [51] |
Deck S, et al. Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to Reθ=13650[J]. Journal of Fluid Mechanics, 2014, 743: 202-248. DOI:10.1017/jfm.2013.629 (  0) 0) |
| [52] |
Ge M, Xu C, Cui G. Transient response of Reynolds stress transport to opposition control in turbulent channel flow[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(2): 320-328. DOI:10.1007/s11433-010-4206-8 (  0) 0) |
| [53] |
Dai Y J, et al. Direct numerical simulation of turbulent flow in a rotating square duct[J]. Physics of Fluids, 2015, 27(6). (  0) 0) |
| [54] |
Hama F R. Boundary layer characteristics for smooth and rough surfaces[J]. Trans. Soc. Nav. Arch. Marine Engrs., 1954, 62: 333-358. (  0) 0) |
| [55] |
Wu Y, Christensen K T. Spatial structure of a turbulent boundary layer with irregular surface roughness[J]. Journal of Fluid Mechanics, 2010, 655(1): 380-418. (  0) 0) |
| [56] |
Coleman H, Hodge B, Taylor R. A re-evaluation of Schlichting's surface roughness experiment[J]. Journal of Fluids Engineering, 1984, 106(1): 60-65. DOI:10.1115/1.3242406 (  0) 0) |
| [57] |
Bandyopadhyay P R. Rough-wall turbulent boundary layers in the transition regime[J]. Journal of Fluid Mechanics, 1987, 180: 231-266. DOI:10.1017/S0022112087001794 (  0) 0) |
| [58] |
Waigh D, Kind R. Improved aerodynamic characterization of regular three-dimensional roughness[J]. AIAA Journal, 1998, 36(6): 1117-1119. DOI:10.2514/2.491 (  0) 0) |
| [59] |
Perry A E, Schofield W H, Joubert P N. Rough wall turbulent boundary layers[J]. Journal of Fluid Mechanics, 1969, 37(2): 383-413. DOI:10.1017/S0022112069000619 (  0) 0) |
| [60] |
Townsend A A. The structure of turbulent shear flow[C]//2nd ed. 1976, Cambridge, UK:Cambridge University Press. 429.
(  0) 0) |
| [61] |
Schultz M P, Flack K A. Turbulent boundary layers over surfaces smoothed by sanding[J]. Journal of Fluids Engineering, 2002, 125(5): 863-870. (  0) 0) |
| [62] |
Keirsbulck L, et al. Surface roughness effects on turbulent boundary layer structures[J]. Journal of Fluids Engineering, 2002, 124(1): 127-135. DOI:10.1115/1.1445141 (  0) 0) |
| [63] |
Tachie M F, Balachandar R, Bergstrom D J. Rough wall turbulent boundary layers in shallow open channel flow[J]. Journal of Fluids Engineering, 2000, 122(3): 533-541. DOI:10.1115/1.1287267 (  0) 0) |
| [64] |
Krogstadt P A, Antonia R A. Surface roughness effects in turbulent boundary layers[J]. Experiments in Fluids, 1999, 27(5): 450-460. DOI:10.1007/s003480050370 (  0) 0) |
| [65] |
Flack K A, Schultz M P, Shapiro T A. Experimental support for Townsend's Reynolds number similarity hypothesis on rough walls[J]. Physics of Fluids, 2005, 17(17): 35102-35110. (  0) 0) |
| [66] |
Morrillwinter C, et al. Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers-ERRATUM[J]. Journal of Fluid Mechanics, 2016, 795: 210-240. DOI:10.1017/jfm.2016.196 (  0) 0) |
| [67] |
Volino R J, Schultz M P, Flack K A. Turbulent structure in rough and smooth wall boundary layers[J]. Advances in Turbulence XI, 2007, 44-46. (  0) 0) |
| [68] |
Volino R J M, Schultz P, FLACK K A. Turbulence structure in boundary layers over periodic two-and three-dimensional roughness[J]. Journal of Fluid Mechanics, 2011, 676(3): 172-190. (  0) 0) |
| [69] |
Schultz M P, Flack K A. Turbulence structure in a boundary layer with two-dimensional roughness[J]. Journal of Fluid Mechanics, 2009, 635(3): 75-101. (  0) 0) |
| [70] |
Flack K. Roughness effects on wall-bounded turbulent flows[J]. Physics of Fluids, 2014, 26(10): 133-156. (  0) 0) |
| [71] |
Wang J, et al. The effects of bed roughness on the distribution of turbulent intensities in open-channel flow[J]. Journal of Hydraulic Research, 1993, 31(1): 89-98. DOI:10.1080/00221689309498862 (  0) 0) |
| [72] |
Wang J J. Distribution of turbulent intensity in a gravel-bed flume[J]. Experiments in Fluids, 1991, 11(2): 201-202. (  0) 0) |
| [73] |
Tao J. Critical instability and friction scaling of fluid flows through pipes with rough inner surfaces[J]. Physical Review Letters, 2009, 103(26): 264502. DOI:10.1103/PhysRevLett.103.264502 (  0) 0) |
| [74] |
Zhang Y, Che D. Effects of two-dimensional V-shaped grooves on turbulent channel flow[J]. Experiments in Fluids, 2012, 52(2): 315-328. DOI:10.1007/s00348-011-1223-y (  0) 0) |
| [75] |
Acarlar M S, Smith C R. A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance[J]. Journal of Fluid Mechanics, 1987, 175: 1-41. DOI:10.1017/S0022112087000272 (  0) 0) |
| [76] |
Klebanoff P, Cleveland W, Tidstrom K. On the evolution of a turbulent boundary layer induced by a three-dimensional roughness element[J]. Journal of Fluid Mechanics, 1992, 237: 101-187. DOI:10.1017/S0022112092003379 (  0) 0) |
| [77] |
Ergin F, White E. Unsteady and transitional flows behind roughness elements[J]. AIAA Journal, 2006, 44(11): 2504-2514. DOI:10.2514/1.17459 (  0) 0) |
| [78] |
Doolittle C J, Drews S D, Goldstein D B. Near-field flow structures about subcritical surface roughness[J]. Physics of Fluids, 2014, 26(12): 487-488. (  0) 0) |
| [79] |
Wang J J, Ding H H. Investigation of semi-spheres on the boundary layer development over a smooth circular plate[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(4): 1-9. (  0) 0) |
| [80] |
Zhang C, Pan C, Wang J J. Evolution of vortex structure in boundary layer transition induced by roughness elements[J]. Experiments in Fluids, 2011, 51(5): 1343-1352. DOI:10.1007/s00348-011-1152-9 (  0) 0) |
| [81] |
Grass A J, Stuart R J, Mansourtehrani M. Common vortical structure of turbulent flows over smooth and rough boundaries[J]. AIAA Journal, 1900, 31(31): 837-847. (  0) 0) |
| [82] |
Grass A J. Structural features of turbulent flow over smooth and rough boundaries[J]. Journal of Fluid Mechanics, 1971, 50(2): 233-255. DOI:10.1017/S0022112071002556 (  0) 0) |
| [83] |
Pearson B R, Elavarasan R, Antonia R A. Effect of a short roughness strip on a turbulent boundary layer[J]. Applied Scientific Research, 1997, 59(1): 61-75. DOI:10.1023/A:1000861915585 (  0) 0) |
| [84] |
Pa K, Ra A. Structure of turbulent boundary layers on smooth and rough walls[J]. Journal of Fluid Mechanics, 1994, 277(277): 1-21. (  0) 0) |
| [85] |
Christensen K T, Adrian R J. Statistical evidence of hairpin vortex packets in wall turbulence[J]. Journal of Fluid Mechanics, 2001, 431(431): 433-443. (  0) 0) |
| [86] |
Bhaganagar K, Kim J, Coleman G. Effect of roughness on wall-bounded turbulence[J]. Flow Turbulence & Combustion, 2004, 72(2): 463-492. (  0) 0) |
| [87] |
Ashrafian A, Andersson H I, Manhart M. DNS of turbulent flow in a rod-roughened channel[J]. International Journal of Heat & Fluid Flow, 2004, 25(3): 373-383. (  0) 0) |
| [88] |
Guala M, et al. Vortex organization in a turbulent boundary layer overlying sparse roughness elements[J]. Journal of Hydraulic Research, 2012, 50(5): 465-481. DOI:10.1080/00221686.2012.729229 (  0) 0) |
| [89] |
Wu Y, Christensen K T. Outer-layer similarity in the presence of a practical rough-wall topography[J]. Physics of Fluids, 2007, 19(8): 425-441. (  0) 0) |
| [90] |
Barros, et al. Observations of turbulent secondary flows in a rough-wall boundary layer[J]. Journal of Fluid Mechanics, 2014, 748(2): 184-195. (  0) 0) |
| [91] |
Lu H, Wang B, Zhang H Q, et al. Effects of different size roughness elements on near-wall turbulence coherent structures[J]. Journal of Engineering Thermophysics, 2010, V31(7): 1143-1147. (in Chinese) 卢浩, 王兵, 张会强, 等. 不同粒径粗糙元对壁面湍流拟序结构的影响[J]. 工程热物理学报, 2010, V31(7): 1143-1147. (  0) 0) |
| [92] |
Lu H, Wang B, Zhang H Q, et al. Effects of roughness elements in different spanwise interval arrayal on near-wall turbulence coherent structures[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(5): 83-87. (in Chinese) 卢浩, 王兵, 张会强, 等. 展向不同间距壁面粗糙元对近壁湍流拟序结构的影响[J]. 实验流体力学, 2010, 24(5): 83-87. (  0) 0) |
| [93] |
Wang J J, Chen G. Experimental studies on the near wall turbulence coherent structures over riblets surfaces[J]. Acta Aeronautica ET Astronautica Sinica, 2001, 22(5): 400-405. (in Chinese) 王晋军, 陈光. 沟槽面湍流边界层近壁区拟序结构实验研究[J]. 航空学报, 2001, 22(5): 400-405. (  0) 0) |
| [94] |
Zhang X, Pan C, Shen J Q, et al. Effect of surface roughness element on near wall turbulence with zero-pressure gradient[J]. Science China:Physics Mechanics & Astronomy, 2015, 58(6): 1-8. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35