融合体布局(Blended Wing Body, BWB),是一种重要的飞行器非常规气动布局形式,因其外形扁平,机翼和机身完全融合在一起,很难分辨出机身与机翼的分界面,如同一个巨大的机翼的而得名。
按照波音公司LIEBECK的测算,融合体布局飞机(BWB)与同装载的常规构型飞机相比, 浸润面积减小约33%,巡航升阻比提高20%以上[1-2]。鉴于融合体布局飞机气动效能上的巨大优势,美国NASA、波音公司、欧洲空客公司,俄罗斯中央流体研究院等从20世纪80年代开始,已经开展了诸多富有成效的研究,如NASA早期的“未来运输机”计划、波音公司的BWB-450方案、NASA近期的X48A/B/C缩比飞行验证研究、欧洲VELA系列研究等。这些项目极大推动了翼身融合体布局的发展。[3]
虽然,融合体布局的气动阻力能够显著低于同等常规飞机,但是所减小的阻力主要源于因外露面积减少而收益的摩擦阻力及附加阻力。对于融合体布局的复杂曲面外形,跨声速飞行的激波阻力问题仍存在,而且必须非常重视。与常规构型飞机相比,融合体布局飞机无尾翼或尾力臂较短,因此其纵向配平能力比较弱,这要求其机翼设计必须考虑较小的低头力矩。现代大型客机所采用的超临界翼型具有较优秀的跨声速阻力特性,其特点是采用前缘钝头、上表面平坦、后缘大反弯[4]。由于后缘大反弯,常规超临界翼型的低头力矩偏大,并不特别适合融合体布局。融合体布局飞机需要一种新的跨声速翼型,既具备常规超临界翼型优秀的跨声速特性,又具有较小的低头力矩。
1 问题描述某融合体布局民机翼要求在巡航点具有高的升阻比,同时具有高阻力发散马赫数,保证抖振边界安全和好的低速特性,根据前面的分析和具体的设计状态可以得到翼型设计要求如下:
1) 巡航点:马赫数Ma=0.73,升力系数CL=0.52,雷诺数Re=6.0×106,要求阻力系数CD尽量小,俯仰力矩系数CM>-0.06;
2) 阻力发散要求:CL=0.52, 阻力发散马赫数Madiv> 0.75;
3) 抖振边界:Ma=0.73, 抖振升力系数CLdiv>0.68;
4) 低速边界:Ma=0.2,最大升力系数CLmax>1.2,并且失速缓和;
5) 非设计点与设计点具有良好的衔接特性,即要求气动特性变化趋势单调光滑连续;
6) 几何约束:相对厚度t/c≥12%。
上面的问题可建立如下优化模型:
| $ \begin{array}{l} {\rm{objective \;min}}\;{C_D}_{{\rm{cruise}}}\\ {\rm{Subject \;to:}}\;M{a_{{\rm{div}}}}{\rm{ > 0}}{\rm{.75}}\\ {C_M}_{{\rm{cruise}}}{\rm{ > - 0}}{\rm{.06}}\\ {C_L}_{{\rm{div}}}{\rm{ > 0}}{\rm{.68}}\\ {C_L}_{{\rm{max}}}{\rm{ > 1}}{\rm{.2}}\\ t/c \ge 12{\rm{\% }} \end{array} $ | (1) |
问题(1) 是一个单目标多约束问题,约束多而严格,甚至不一定存在可行解。因此,该翼型设计的基本思想是先找可行解,再由可行解寻找最优解。具体设计流程如下:
1) 挑选适当初始翼型,并进行气动力分析;
2) 根据设计要求,基于数值计算构建“人在回路”的多点多目标多约束设计气动优化平台。由于初始翼型可能不满足所有约束,初步优化中需将部分约束转换为朝向约束阈值的目标,优化目的为寻找可行解;
3) 采用多目标遗传算法进行初步充分寻优;
4) 对寻优结果进行分析,采集满足各种约束的可行解(最优解);
5) 由于各目标及各约束之间相互矛盾,初步寻优,并不一定能获得可行解。根据设计要求和优化结果分布,不断调整优化目标及约束,进行多轮次迭代寻优,直到获得可观的可行解分布;
6) 引入可行解进入优化样本点,调整优化目标及约束,继续进行多目标寻优,直到获得理想的最优解分布;
7) 对优化结果进行分析,挑选最优解。
2.2 特殊处理 2.2.1 低速最大升力系数优化过程中对翼型低速最大升力系数并不直接进行计算,选择的初步翼型其恰好满足这一要求(需要一定的经验),优化过程中参考初步翼型的几何特征,约束翼型的前缘半径和前缘钝度。
2.2.2 低亚声速状态优化流程中增加一个状态点:Ma=0.7,CL=0.52,要求该点的阻力系数不得大于巡航点的阻力系数,确保非设计点与设计点具有良好的衔接性。
2.2.3 压力分布按照超临界翼型上表面压力分布的基本特征,要求在巡航点,翼型上表面压力吸力峰值对应马赫数小于1.2,允许出现适当的逆压梯度以及超声速平顶区,激波后允许出现压力平台或二次缓慢加速区,但不得出现二次激波或二次强压缩。翼型下表面压力变化连续,不允许出现超声速区。这种压力分布特征并非对应最小阻力值,但可保证巡航机翼表面流动的稳定性,以及气动力随速度变化的单调性[5-6]。
2.2.4 抖振边界与阻力发散严格约束不利于机器自动寻优,以及快速有效找到可行解。根据经验,这里对抖振边界和阻力发散约束进行如下转换处理:
抖振边界点约束转换为:Ma=0.73,CL=0.68,对其阻力系数最小化寻优或约束小于某一值。
阻力发散点约束转换为:Ma=0.75,CL=0.52,对其阻力系数最小化寻优或约束小于某一值。
翼型抖振边界一般通过升力线斜率是否降低或俯仰力矩系数-升力系数曲线是否柺折进行判断。翼型跨声速抖振是由于强激波引发分离,导致升力线线性段特征破坏。通过优化阻力控制抖振边界,一方面可有效减小计算量;另一方面,将强约束转换为目标,更有利于寻优推进,快速找到可行解。
3 设计平台 3.1 翼型参数化翼型参数化采用美国波音公司Kulfan等提出的基于型函数/类函数变换的参数化方法(Class function/Shape function Transformation, CST)[7-8],该方法控制参数少,几何意义明确、精度较好。CST方法对翼型参数化的表达式如下:
翼型上、下表面分别为:
| $ {y_u} = C\left( x \right)\cdot{S_u}\left( x \right) + x\cdot{y_{TEu}} $ | (2) |
| $ {y_l} = C\left( x \right)\cdot{S_l}\left( x \right) + x\cdot{y_{TEl}} $ | (3) |
其中,yTEu、yTEl分别为翼型上、下表面后缘的纵坐标。
| $ 类函数定义:C\left( x \right) = {x^{N1}}\cdot{\left( {1 - x} \right)^{N2}} $ | (4) |
| $ 型函数定义:{S_u}\left( x \right) = \sum\limits_{i = 0}^N {{A_{{u_i}}}\cdot{S_i}\left( x \right)} ; $ | (5) |
| $ {S_l}\left( x \right) = \sum\limits_{i = 0}^N {{A_{{l_i}}}\cdot{S_i}\left( x \right)} $ | (6) |
其中,
| $ {S_i}\left( x \right) = \frac{{N!}}{{i!\left( {N - i} \right)!}}{x^i}{\left( {1 - x} \right)^{N - i}}; $ |
N1和N2分别取0.5和1.0;Aui和Ali为待定系数;Si(x)为Bernstein多项式。
Kulfan经过推导指出,Au0和Al0与翼型的前缘半径有直接联系:
| $ {A_{{u_0}}} = - {A_{{l_0}}} = 2\sqrt {{R_{LE}}} $ | (7) |
由上述分析可知,只要控制系数Aui和Ali,就可控制翼型几何外形。
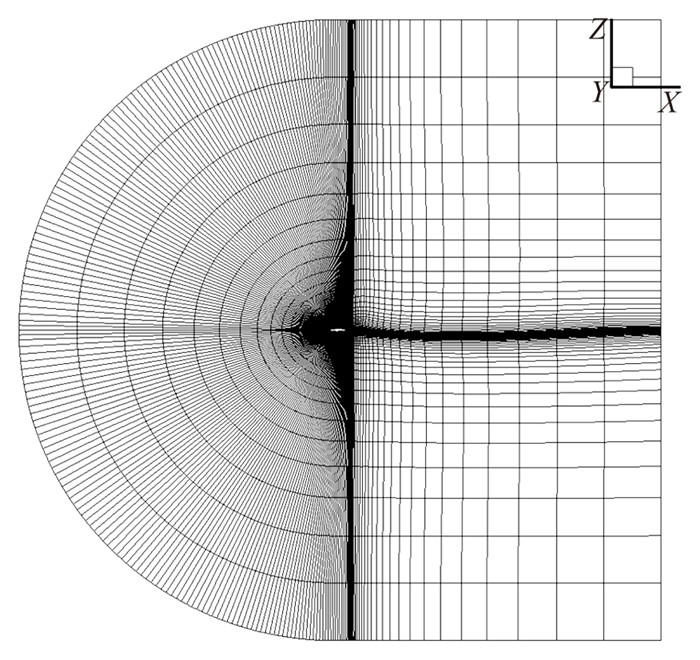
3.2 计算网格计算网格生成与更新:根据翼型单位几何外形,采用基于无限插值算法生成初始网格,再由椭圆方程进行光顺处理的C型结构网格,如图 1所示。网格规模:240×70,壁面第一层网格2.0×10-6,法向增长率1.2。
|
图 1 C型结构网格 Figure 1 C-type structural mesh |
气动力解算采用三维雷诺平均Navier-Stokes方程(RANS)求解程序,CCFD-MB[9]。该程序基于有限体积法和多块结构网格求解RANS方程,湍流模型包括SA一方程模型和Menter-SST两方程模型。
三维积分形式的雷诺平均Navier-Stokes方程:
| $ \frac{\partial }{\partial t}\iiint{\mathit{\pmb{Q}}\text{d}}V+\iint{\mathit{\pmb{f}} \cdot \mathit{\pmb{n}}}{\text{d}}S=0 $ | (8) |
式中,V为控制体体积,S为控制体表面面积,Q为守恒量,f为通过表面S的无粘通量和粘性通量之和,n为控制体表面S的外法向单位矢量。以有限体积法构造空间半离散格式,无粘通量项采用二阶Roe迎风通量差分格式离散,粘性通量项采用中心差分格式离散,隐式时间推进,采用多重网格技术加速收敛。
3.4 优化算法对于多目标问题,优化解表现为一个解集,即Pareto前端(Pareto Frontier)。设计人员根据Pareto前端的分布进行多目标决策,获得最终的优化解。多目标遗传算法是求解多目标优化问题Pareto前端的最有效方法之一,已经有很多成功的应用。遗传算法(GA)借鉴生物进化的思想,通过计算机模拟物种繁衍父代遗传基因的重新组合与“优胜劣汰”自然选择机制的联合作用,解决科学与工程中的复杂问题[10]。NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm Ⅱ)是目前公认效果最好的多目标优化遗传算法之一[11]。该算法根据产生的各种非劣前沿,采用了一种快速的非支配排序方法,从而减少了算法运行的整体时间。NSGA-Ⅱ还使用了排挤算法来代替共享函数算法,使其无需确定一个共享参数就能控制个体的分布;并引入了精英保留策略,提高种群的整体进化水平。在约束处理面,NSGA-Ⅱ算法加入了一种高效的约束处理机制,其不采用任何罚函数方法,而是通过引入一种虚拟的越界值,为所有的等式或不等式约束条件提供了一种通用解决方案。
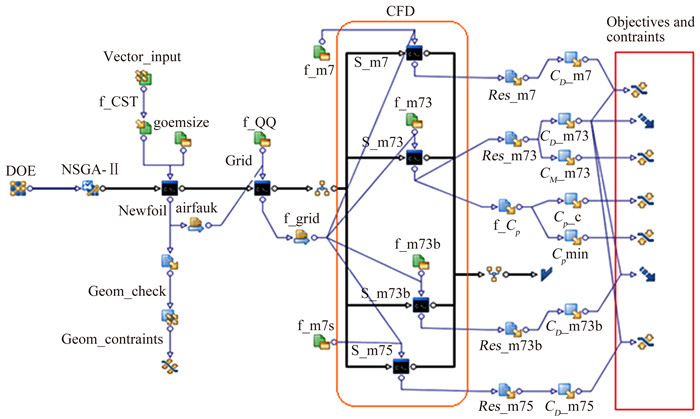
3.5 优化平台优化平台(图 2)基于意大利ECTECO公司开发的modeFRONTIER软件搭建。modeFRONTIER软件是当今世界多学科设计优化领域最著名的软件平台之一。该软件不仅提供了大量优秀的优化算法、试验设计算法、响应面模型,还提供了各种主流CAE软件、编程语言和系统脚本的集成模块,人机界面友好,可快速按照设计意图建立起各种逻辑的优化流程;优化过程中,允许随时中断,进行种群、目标或约束等的干预或调整,符合“人在回路”的设计思想,易于实现多轮迭代优化设计[12]。
|
图 2 气动多点多约束优化设计平台 Figure 2 Multi-point multi-constraint aerodynamic optimization platform |
表 1给出了初始翼型气动力信息。初始翼型在升阻特性方面,基本满足设计要求,但不满足力矩系数CM约束要求。可见,初始翼型为非可行解。
| 表 1 初始翼型气动力数据 Table 1 Aerodynamic data about INI airfoil |
|
|
初步优化的目的是:(1) 继续提高翼型巡航升阻特性(气动效率);(2) 寻找满足力矩特性约束要求,获得可行解;(3) 获得各目标及主要约束的分布特征。
因此,初步优化除将各工况的阻力系数作为优化目标之外,还将巡航点的力矩系数CMm73最大化纳入优化目标。这样,初步优化的目标数目达到4个。经处理后优化问题化为:
| $ \begin{align} &\text{objective}\ \text{min}({{C}_{D}}_{\text{m}73},{{C}_{D}}_{\text{m75}},{{C}_{D}}_{\text{m73b}},{{C}_{M}}_{\text{m73}}) \\ &\text{subject}\ \text{to}:t/c\ge 12% \\ \end{align} $ | (9) |
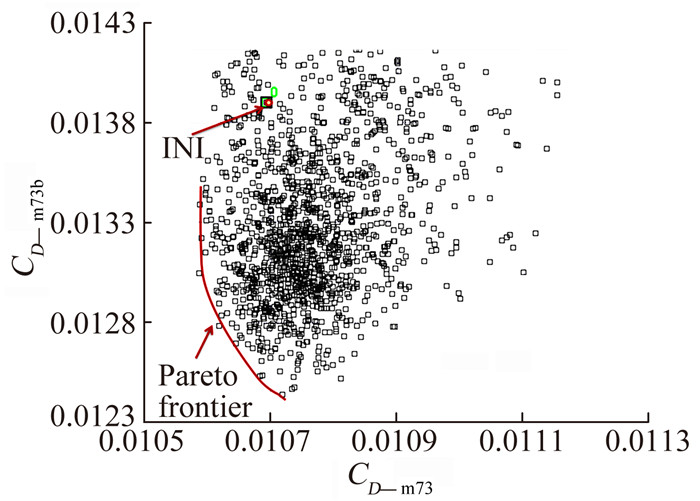
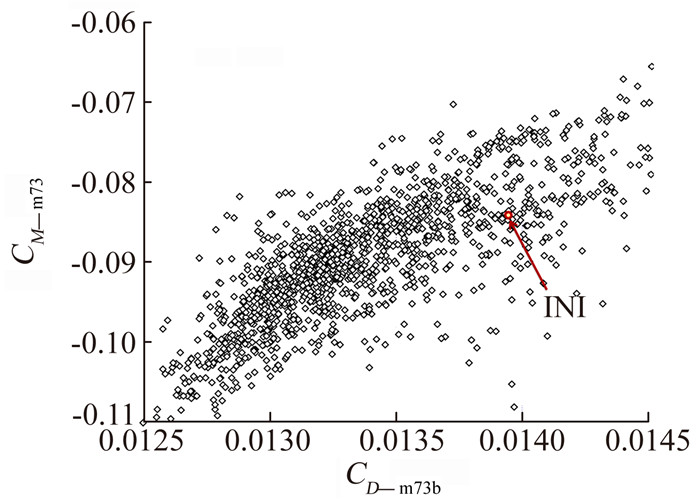
基于空间均匀随机算法产生40个样本点构成初始优化种群,采用NSGA-Ⅱ算法优化50代,获得初步优化解分布,如图 3。INI为初始翼型,CD_m73为巡航点的阻力系数,CD_m73b为抖振边界点的阻力系数。相比初始值,CD_m73b的优化效果最为明显。图 3、图 4显示,初步优化得到了各工况的阻力系数分布的Pareto前端,但是巡航点力矩系数CM_m73仍未能满足约束要求(见图 5),即初步优化未能获得可行解。分析认为,可能因为优化目标过多,各目标之间相互掣肘,导致力矩系数未能向希望方向大幅逼近。
|
图 3 巡航点阻力系数与抖振边界点阻力系数分布 Figure 3 Distribution of cruise drag coefficient and buffet onset boundary drag coefficient |
|
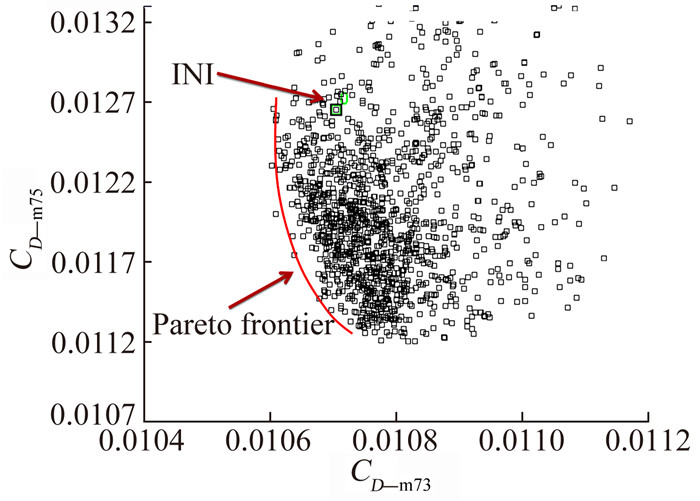
图 4 巡航点阻力系数与马赫数发散点阻力系数分布 Figure 4 Distribution of cruise drag coefficient and Mach number divergence drag coefficient |
|
图 5 巡航点力矩系数与抖振边界点阻力系数分布 Figure 5 Distribution of cruise pitch moment coefficient and buffet onset boundary drag coefficient |
图 4显示,马赫数阻力发散控制的优化目标较易实现。
4.2 二次优化二次优化的目的是在初步优化结果的基础上,集中精力优化俯仰力矩系数,使之满足约束要求,获得可行解。
二次优化不再将阻力发散点工况的阻力系数CD_m75作为优化目标,而是与巡航点的阻力系数建立约束关系,要求之间的阻力差小于0.0020。
初步优化发现巡航点阻力系数CD_m73下降较小,说明该点激波较弱,优化收益不大,故将CD_m73定为约束,要求小于0.0107。这样二次优化的目标数减少为2个。优化模型为:
| $ \begin{array}{l} {\rm{objective}}\;{\rm{min}}({C_D}_{{\rm{m73b}}},{C_M}_{{\rm{m73}}})\\ \;\;{\rm{Subject}}\;{\rm{to}}:t/c \ge 12\% \\ \;\;\;\;\;\;\;\;{C_D}_{{\rm{m75}}} - {C_D}_{{\rm{m73}}} < 0.002\\ \;\;\;\;\;\;\;\;{C_D}_{{\rm{m73}}} < 0.0107 \end{array} $ | (10) |
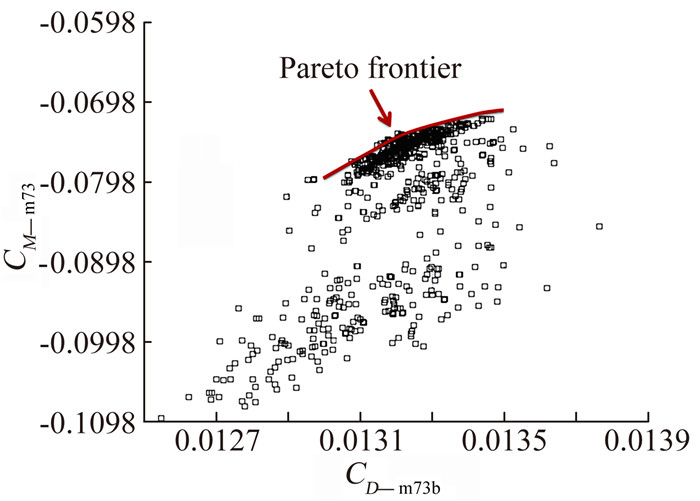
建立新约束后,从上轮结果可行解中挑选样本点若干,组成新优化种群,优化30代,结果如图 6。可见,减小目标数后,巡航点力矩系数CMm73优化获得有效推进,但是仍未满足约束要求。
|
图 6 巡航点力矩系数与抖振边界点阻力系数分布 Figure 6 Distribution of cruise drag coefficient and buffet onset boundary drag coefficient |
再次优化的目的是在二次优化结果的基础上,进一步集中精力优化俯仰力矩系数,使之满足约束要求,获得可行解分布。
再次优化不再将抖振边界点阻力系数CDm73b作为目标,仅作为约束,要求小于0.0135;这样优化目标仅剩CMm73。
| $ \begin{array}{l} {\rm{Objective}}\;{\rm{min}}\;{C_M}_{{\rm{m73}}}\\ \;\;{\rm{Subject}}\;{\rm{to}}:t/c \ge 12\% \\ \;\;\;\;\;\;\;{C_D}_{{\rm{m75}}} - {C_D}_{{\rm{m73}}} < 0.002\\ \;\;\;\;\;\;\;{C_D}_{{\rm{m73}}} < 0.0107\\ \;\;\;\;\;\;\;{C_D}_{{\rm{m73b}}} < 0.135 \end{array} $ | (11) |
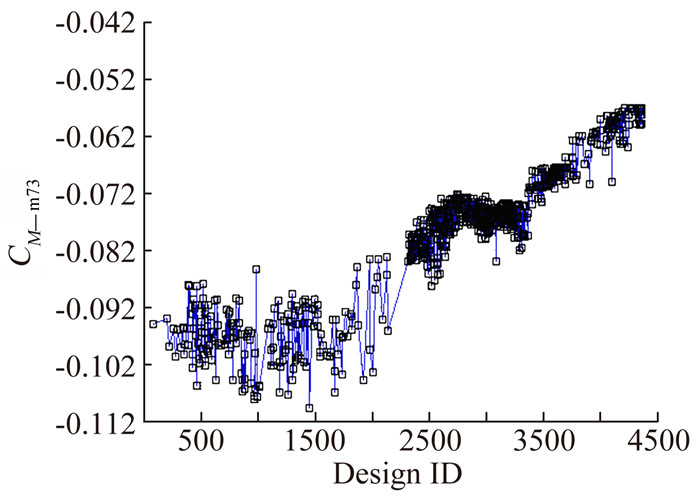
从上轮解分布中挑选样本点组成新的优化种群,优化30代。优化结果如图 7,缩减目标后,尽管面临严格的各种约束限制,本轮优化仍获得大量可行解,巡航点力矩系数CM_m73大幅改进,原设计问题的可行解分布已经找到。
|
图 7 巡航点力矩系数优化曲线 Figure 7 Optimization curve forcruise pitch moment coefficient |
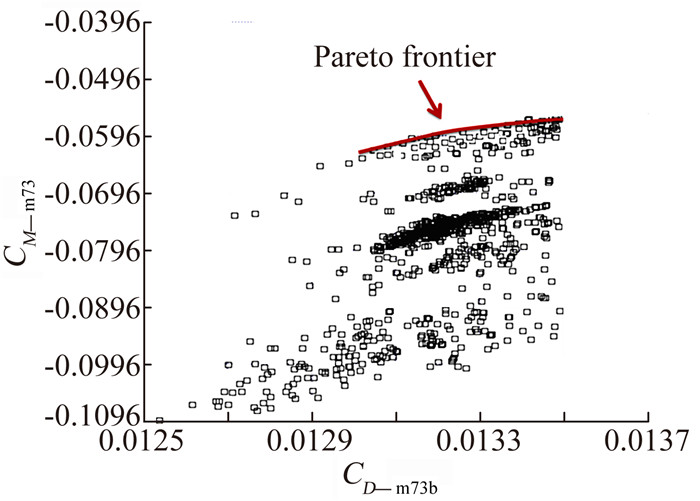
从可行解中挑选样本重新构建初始优化种群,将抖振边界点阻力系数CD_m73b最小化再次作为优化目标之一,原约束不变,优化若干代,获得较为丰满的Pareto前端,如图 8。
自此,获得了原设计问题充足的可行解及优化解分布。
|
图 8 巡航点力矩系数与抖振边界点阻力系数分布 Figure 8 Distribution of cruise pitch moment coefficient and buffet onset boundary drag coefficient |
最终优化在上轮可行解基础上对原设计问题再次充分寻优,获得更为精细的最优解分布。
最终优化设置:调整巡航点力矩系数CMm73为约束,要求大于-0.0605;调整设计目标为:巡航点阻力系数CDm73最小和抖振边界阻力系数CDm73b最小。
| $ \begin{array}{l} {\rm{Objective}}\;{\rm{min}}({C_D}_{{\rm{m73b}}},{C_D}_{{\rm{m73}}})\\ \;\;{\rm{Subject}}\;{\rm{to}}:t/c \ge 12\% \\ \;\;\;\;\;\;\;{C_D}_{{\rm{m75}}} - {C_D}_{{\rm{m73}}} < 0.002\\ \;\;\;\;\;\;\;{C_D}_{{\rm{m73}}} > - 0.5605 \end{array} $ | (12) |
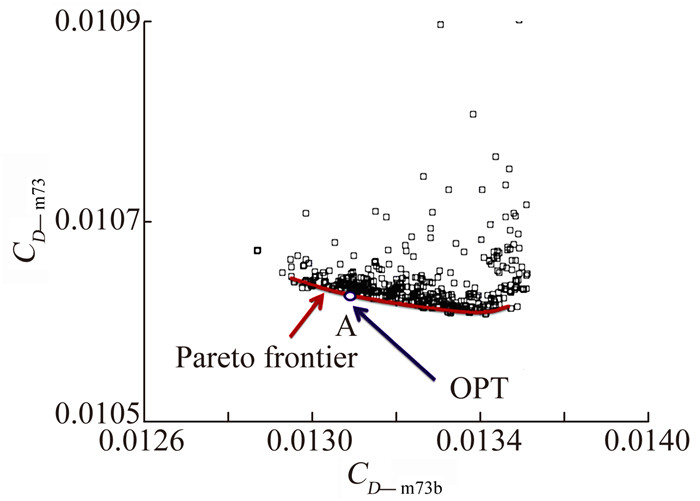
从上轮可行解中挑选若干样本点,采用NSGAⅡ算法进行双阻力目标优化,得到如图 9的Pareto前端分布。根据经验,从Pareto前端中挑选A点作为本次设计的最优解(OPT)。
|
图 9 巡航点阻力系数与抖振边界点阻力系数分布 Figure 9 Distribution of cruise drag coefficient and buffet onset boundary drag coefficient |
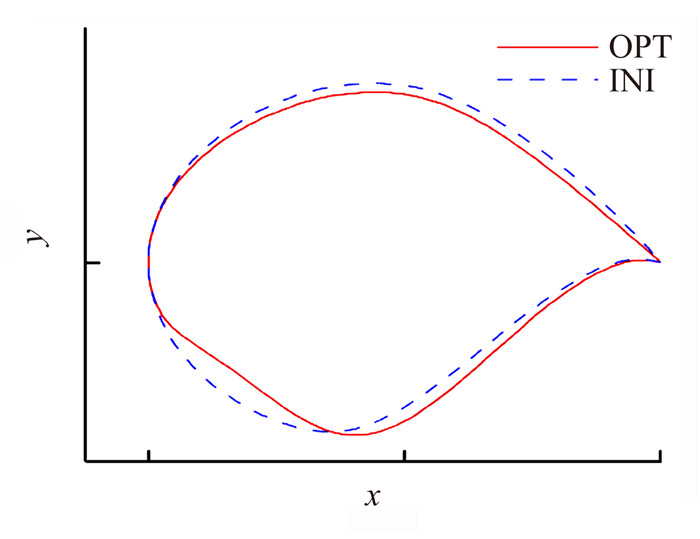
图 10给出了优化翼型(OPT)与原始翼型(INI)的几何对比,可见优化翼型具有明显的前加载特征。表 2为最终优化翼型的气动力结果,可见:优化翼型巡航点阻力比初始翼型的略小,但巡航力矩系数已满足设计要求,阻力发散马赫数满足要求;抖振边界不低于原翼型。
|
图 10 优化翼型与初始翼型几何对比 Figure 10 Geometric comparison between OPT airfoil and INI airfoil |
| 表 2 优化翼型各工况气动力数据 Table 2 Aerodynamic data about OPT airfoil |
|
|
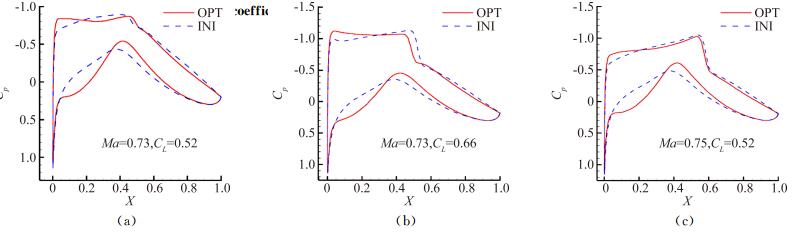
图 11为优化翼型(OPT)与初始翼型(INI)在各工况的压力分布对比,可见巡航工况,优化翼型上表面具有良好的超临界特征,保持弱激波。
|
图 11 优化翼型与初始翼型各工况压力分布对比 Figure 11 Comparison of pressure coefficient between OPT airfoil and INI airfoil |
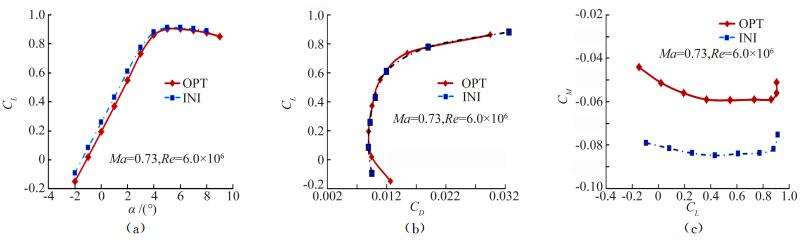
图 12为优化翼型(OPT)与初始翼型(INI)在巡航马赫数的气动力对比,可见优化翼型的升阻特性稍优于初始翼型,满足抖振边界要求,并且力矩特性显著优于初始翼型。
|
图 12 优化翼型与初始翼型在巡航马赫数的气动力对比 Figure 12 Comparison of aerodynamic curves between OPT airfoil and INI airfoil at cruise Mach number |
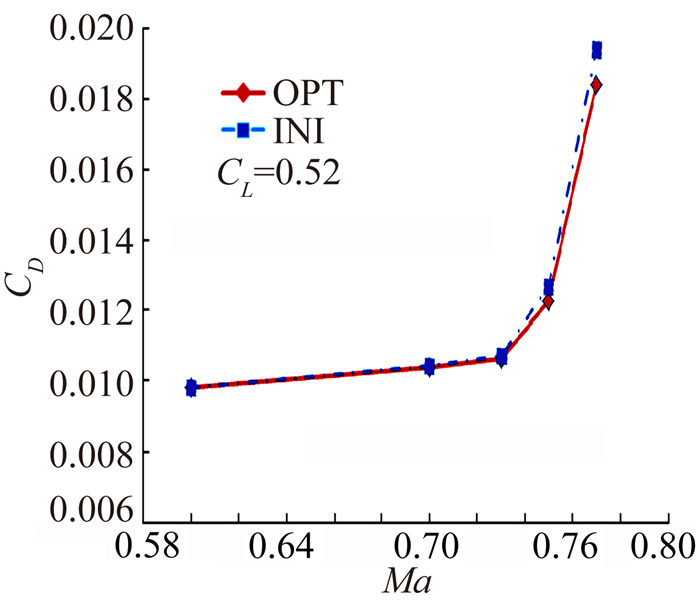
图 13为优化翼型(OPT)与初始翼型(INI)的阻力发散特性,优化翼型满足力矩发散要求,发散马赫数大于0.75。
|
图 13 优化翼型与初始翼型的阻力发散特性 Figure 13 Comparison of drag divergence between OPT airfoil and INI airfoil |
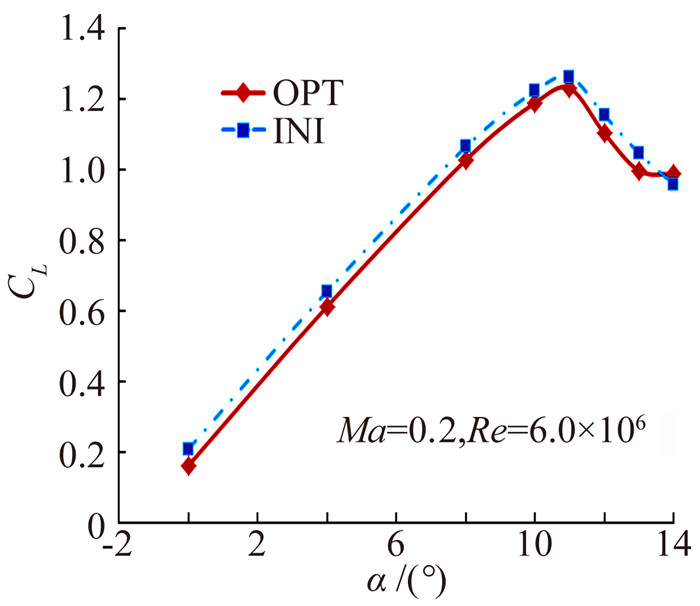
图 14为优化翼型(OPT)与初始翼型(INI)的低速气动特性,优化翼型低速特性与初始翼型相当,最大升力系数比初始翼型略小,但仍大于1.2,满足要求。
|
图 14 优化翼型与初始翼型的低速升力系数特性 Figure 14 Comparison of lift curves between OPT airfoil and INI airfoil at low speed condition |
针对跨声速融合体布局飞机,开展所需超临界翼型的气动力设计研究,采用多目标气动优化技术,经过多轮迭代优化完成了翼型设计,有以下结论:
1) 优化翼型具备优秀的高亚声速气动特性,巡航点马赫数Ma=0.73,升力系数CL= 0.52,弱激波特征,俯仰力矩系数CM=-0.06;阻力发散马赫数Madiv超过0.75,抖振升力系数CLdiv大于0.68;
2) 优化翼型具有常规超临界翼型的基本气动力特征,满足阻力发散和抖振边界要求;同时具有明显前加载特征,低头力矩大幅低于常规超临界翼型,满足融合体布局飞机气动力要求;
3) 本设计方法可从一个非可行解出发找到可行解,并继续优化得到最优解,适用于探索新问题以及经验不足下的翼型设计。
| [1] |
Liebeck R H, Page M A, Rawdon B K, et al. Concepts for advanced subsonic transports[R]. NASA CR 4624, Sept. 1994.
(  0) 0) |
| [2] |
Liebeck R H. Blended wing body design challenges[R]. AIAA 2003-2659, 2003.
(  0) 0) |
| [3] |
Li X Q, Zhang M, Lu S F, et al. Advances in aerodynamics for blended wing body aircraft[J]. Aircraft Design, 2007, 27(2): 1-9. (in Chinese) 李晓勇, 张淼, 鲁素芬, 等. 翼身融合飞机的空气动力学研究进展[J]. 飞机设计, 2007, 27(2): 1-9. (  0) 0) |
| [4] |
Dang T H. Development of NASA supercritical airfoils[J]. Design and Investigation of Civil Aircraft, 2005, 2: 29-49. (in Chinese) 党铁红. NASA超临界翼型的发展[J]. 民用飞机设计与研究, 2005, 2: 29-49. DOI:10.3969/j.issn.1674-9804.2005.02.006 (  0) 0) |
| [5] |
Zhang Y F. Aerodynamic optimization of civil aircraft design based on advanced computational fluid dynamics[D]. Beijing:Tsinghua University, 2010. (in Chinese) 张宇飞. 基于先进CFD方法的民用客机气动优化设计[D]. 北京: 清华大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10003-1012006462.htm (  0) 0) |
| [6] |
Sun Z W, Bai J Q, Gao Z H, et al. Design and wind tunnel test investigation of the modern supercritical airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 804-818. (in Chinese) 孙智伟, 白俊强, 高正红, 等. 现代超临界翼型设计及其风洞试验[J]. 航空学报, 2015, 36(3): 804-818. (  0) 0) |
| [7] |
Kulfan B M. Universal parametric geometry representation-method-'CST'[J]. Journal of Aircraft, 2008, 45(1): 142-158. DOI:10.2514/1.29958 (  0) 0) |
| [8] |
Li J, Gao Z H, Huang J T, et al. aerodynamic optimization system based on CST technique[J]. Acta Aerodynamica Sinica, 2012, 40(3): 443-449. (in Chinese) 李静, 高正红, 黄江涛, 等. 基于CST参数化方法气动优化设计研究[J]. 空气动力学学报, 2012, 40(3): 443-449. (  0) 0) |
| [9] |
Li Q, Guo Z D, Deng Y J. CFD high performance computing in aeronautic[J]. J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2011(S1), 39(1):79-82. (in Chinese) 李权, 郭兆电, 邓一菊, 等. 航空CFD高性能计算应用研究[J]. 华中科技大学学报(自然科学版), 2011(S1), 39(1): 79-82. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hzlg2011s1020&dbname=CJFD&dbcode=CJFQ (  0) 0) |
| [10] |
Cui X X. Multi-objective evolutionary algorithm and itsapplication[M]. Beijing: National Defense IndustryPress, 2008. (in Chinese) 崔逊学. 多目标进化算法及其应用[M]. 北京: 国防工业出版社, 2008. (  0) 0) |
| [11] |
Deb K, Pratap A, Agarwal S, et al. A fast andelitist multi-objective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 181-197. (  0) 0) |
| [12] |
Li Q, Guoz D, Let W T, et al. Engineering environment-based multi-objective optimization platformfor aerodynamic design[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1):255-268. (in Chinese) 李权, 郭兆电, 雷武涛, 赵轲. 基于工程环境的气动多目标优化设计平台研究[J]. 航空学报, 2016, 37(1): 255-268. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hkxb201601020&dbname=CJFD&dbcode=CJFQ (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


