过去几十年随着计算机和数值方法、优化算法的迅猛发展,也随着对飞机性能的要求越来越先进、复杂,飞机设计从依赖于风洞实验和试凑(cut-and-try)的状态向基于CFD计算的性能分析和基于优化的自动化设计的方向发展,优化方法在飞机设计中的起到的积极作用已不可否认。然而优化和设计这两个概念在指导思想和关注重点上毕竟存在着一定差距,加之一些其它的原因,使得先进的优化方法在工程设计实际中应用仍然受限。
计算领域的优化(或最优化方法,以单目标优化为例)指在可行域中搜索最优解的过程,其数学形式为
minF(x)
s.t.x∈D
一般称通过优化获得设计结果的过程为优化设计。本文讨论的优化设计是以最优化理论为基础,根据设计所追求的性能目标建立目标函数,在满足给定的约束体系下,通过计算机搜索最优设计方案的过程,其基本过程符合图 1描述的回路:首先定义优化目标及约束,提供初始设计样本进行计算;得到样本几何、性能与约束、目标之间的差异,利用优化算法得到新的设计;进而计算新样本性能并得到新的差异,判断优化是否收敛或者是否产生满足设计人员期望的设计,如果是则停止优化,否则继续优化回路。
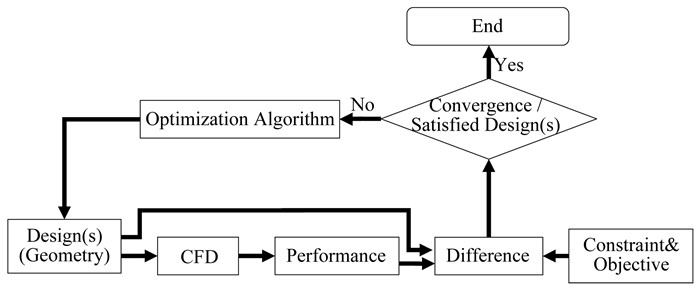
|
图 1 优化设计回路 Figure 1 Optimization design flow chart |
虽然最优化方法的数学定义理论上可以涵盖所有的目标和约束,能够完全按照上述回路封闭、自动地运行。然而在工程应用中,优化目标F、设计变量x、可行域D(对x的约束涵盖在D中,但其他类型的约束在此定义下无法表达)的定义往往存在很多困难,不但过多的目标和约束会导致优化循环难以收敛或获得有效解,而且很多工程约束更是难以给出数学表达。因此目前工程中的优化设计的目标、约束体系相较于工程设计的期望而言往往过于简化,甚至不尽合理,因而很多时候优化设计的结果并不具有工程实际意义。
“人在回路”一词最早出现在反设计方法研究中,其目的在于表述人在设计迭代中的参与。之后“人在回路”的内涵不断充实和调整。本文中定义为:优化过程中,对不便直接体现在优化约束与目标中的工程设计要求,通过人在设计循环中对优化目标、约束、方法、样本等的监视、判断和调整来加以引入。“人在回路”利用“人”更善于综合、模糊判断的优势,通过将人工经验与自动优化相结合,在使优化结果更加符合工程实践要求的同时,可能提高优化效率。
本文第一节介绍优化设计的发展过程和困难,第二节解释“人在回路”的内涵和作用,第三节介绍“人在回路”目前发展趋势和较有前景的研究方向,第四节展望“人在回路”未来研究重点并讨论可能的实现手段。
1 优化设计自飞机发明以来,其设计方法不断演变,从试凑与经验总结中一步步发展,创造了一系列经典与突破。自20世纪八九十年代起,优化、反设计等方法逐渐应用于飞行器研究中,随着计算机计算能力的迅猛发展,优化方法得到了长足的发展。然而长期以来,优化在实际工程设计中发挥的作用仍不如人意,存在诸多困难和障碍。这些困难和障碍使得单纯依靠优化很难获得满足工程需求的设计方案,也阻碍了优化设计更好地替代工程师的工作。
1.1 优化设计的发展在计算机大规模应用之前,工程设计只能依赖于简单的理论公式、繁复的实验数据和“只能意会”的经验,设计师通过积累的数据和经验进行试凑,不断取舍、判断、权衡,以期达到要求。即图 1的设计回路中,寻优任务由人完成,可以说人不但“在回路”,几乎“就是回路”。这一方面使得飞机设计成功与否取决于设计师的经验、认识甚至个性,另一方面也使得设计师的成长和经验的继承变得愈发困难。
在飞机设计严重依赖于人的同时,飞机变得越来越复杂、精密,设计团队越来越庞大。莱特兄弟以两人之力创造了“飞行者一号”,后来Kelly Johnson带领一个十几人的小团队设计了F-80,而在设计波音747时,Joe Sutter的设计团队却从几百人最终膨胀到4500人[1]。在现代飞机设计中,追求极致导致关注的问题、关联的学科、设计的对象、涉及的规律、积累的数据不断增多,在这种“一切影响其他一切”(everything affects everything else[1])的复杂工程中,需要应对的问题开始超出人所能处理的极限。因此,基于计算机的优化方法和数据挖掘方法逐渐应用于飞机设计中,并取得了长足的发展。
在20世纪八九十年代,优化或计算机辅助设计的早期发展阶段,计算机仍只能处理实验-理论/经验公式计算[2]、基于线性速度势方程的面元法[3-5]、亚声速不可压流动基于涡升力理论的涡格法[6-8]等程序。当时工程型号尚不过于复杂,研究或设计往往以获得某方面最优性能为目标,即便如此,人已经表现出效率低、速度慢、认识局限的不足。而计算机程序已经可以很大程度减轻人的工作强度,并获得更好的结果。因此针对“人就是回路”的现实,当时研究的目标是尽量把人“逐出”“回路”,用计算机代替“人”以加快优化速率和效果[9-10]。
这一阶段人们发展出了反设计方法、反优化方法和早期的直接优化方法[11]。尽管根本出发点是减少人的工作,但由于技术尚不成熟,这些方法中仍需要大量人的介入,也为后来“人在回路”的回归埋下了伏笔。
最初的反设计方法(inverse method)中设计师提出目标压力分布,通过求解辅助方程(auxiliary equation)变形几何使其压力分布逼近目标[12-14],设计成功与否取决于设计师给出的目标压力分布是否合理。虽然反设计方法基于的控制方程从二维、势流方程发展到了三维、Euler方程,但仍然只能用于设计简单部件[15-17],一方面是由于计算能力的限制,另一方面也在于设计师不可能给出复杂构型的符合流体力学方程的压力分布。
随着优化算法的发展,人们尝试优化出更优的压力分布来作为反设计的目标,从而发展出了反优化方法(inverse numerical optimization)[18-21]。反优化方法的发展有多方面考虑:一是优化算法得到了一定发展,遗传算法、模拟退火等随机搜索方法和梯度算法开始应用于飞机设计[22];二是计算能力有限导致不能直接应用直接优化方法(direct numerical optimization)[21];三是在复杂要求下,设计师很难直接给出较优的合理目标压力分布[23]。因而反优化方法以压力分布作为优化对象,在给定的升力、力矩、环量分布等约束下优化压力分布[21, 23],得到最优压力分布后,用反设计方法得到相应几何设计。为得到合理的目标压力分布和几何,需要提出相应的约束,如要求压力分布曲线要在后缘保证后加载强度,或局部满足斜率限制以避免流动分离,以及其它方面的合理性等[21, 23-24]。
不同于反优化以压力分布为对象、反设计以压力分布为目标,目前流行的空气动力学直接优化方法通常将几何作为优化对象,用流场计算获得的性能指标来构造适应度函数。在复杂问题面前,人在试凑设计中常表现出顾此失彼、因循守旧、记忆力差、认识局限、搜索空间小等局限,直接优化方法则相应地展现出其优势[25-29],并随着计算能力的提高,迅速得到了研究发展。但迄今为止,大部分发表的工作主要集中于优化算法的发展和应用[30-34]。直至近期,研究者的关注点才逐渐向优化算法在复杂工程实际设计中的应用策略转移。人们在多学科、多设计点、多目标、鲁邦优化方面进行大量研究,以期通过优化手段获得均衡、全面的性能。
多学科、多点、多目标优化等概念虽然在最初阶段含义不尽相同,但最终殊途同归,都一定程度上转化为多目标优化问题。多学科在最初仅指考虑多学科之间耦合效应的设计,当时由于计算能力的限制往往停留于概念或简单部件的研究[35],并未大量使用优化算法,相关发展可以参见综述[36-37]。随着优化算法和计算机的发展,多学科优化实质上趋向于将多学科性能直接作为多个目标,或考虑多学科耦合效应形成多个组合目标的多目标优化问题[28, 38-41]。
多点设计的目的在于不同飞行工况下性能的均衡稳定[42-43],这一思想早在反设计阶段就已经得到应用。不过最初在两个设计点分别反设计,再依据小扰动理论线性加权叠加的做法[44]很快就被淘汰;随后出现了将当前压力分布与目标压力分布间的差异在两个设计点分别计算后加权,再用最小二乘法进行反设计的尝试[45];目前直接优化方法中,早期是将多设计点目标加权后转成单目标优化[42, 46-47],后来才开始使用更加先进的多目标优化手段[48-51]。
多目标优化技术同样在反设计时期起步[52-53],并在优化设计中得到了广泛应用[54-57]。目前多目标优化主要有三类:应用最早的多目标加权为单目标的优化,应用最广泛的基于帕雷托前缘的优化和新兴的基于博弈理论(如Nash均衡)或其他人工智能[58]的优化。多目标加权方法[59]虽然简单,但一般只在明确知道合理的权重时有效,优化效果也显著依赖于权重选择[60]。Shaffer于1985年首先提出了一种多目标遗传算法[61],随后Goldberg发展出了基于帕雷托前缘的优化方法[62],并得到了充分发展[63-66],详细内容可见综述[67]。目前基于帕雷托前缘的多目标优化方法发展成熟,已经广泛应用于实际应用中,但不可否认的是这种方法带来的性能评估计算量迅速增加和收敛困难仍是一大挑战。
鲁棒性本身有多种表述[68-70],本文采用同文献[70]相同的描述:鲁棒性是系统对环境和系统本身变化的响应不敏感的程度(The degree of tolerance of the system to be insensitive to variations in both the system itself and the environment.)[71]。鲁棒性设计优化是由Genichi Taguchi首先提出的用于提高产品鲁棒性的设计方法[70],目前有一些文章中的鲁棒性优化指的是优化方法的鲁棒性[72-73],本文中不予考虑。
传统的直接优化方法往往过分追求设计点的性能,却导致了糟糕的非设计点特性[69],因此鲁棒优化在实际工程设计中显得十分重要。Taguchi的关注重点在于减少产品间的差异以提高产品质量[74-76],与气动设计的鲁棒性不同而且存在一定的局限性[77-78],随后Welch等用计算机实验尝试替代Taguchi方法[79-80],但效果有限;后续又发展出用极小极大策略避免最坏情形[78-82]和利用贝叶斯风险最小化来提高一定不确定范围内性能的方法[83-84];目前比较流行的方法是基于不确定设计的鲁棒性优化,具体发展可详见综述[70]。不确定设计方法通过设计点邻域的性能期望和方差来表征鲁棒性,最初的研究发现单独优化期望会导致非鲁棒结果,单独优化方差则无法有效提升性能,因此需要进行期望-方差的多目标优化,使用的多目标优化方法与上文类似,更多内容可参考文献[69]。但显然鲁棒优化对计算量的增加是相当可观的。
1.2 优化设计的困难优化算法近年来已取得巨大的发展,但优化设计在工程设计中的应用却与之不太相称。目前的飞行器气动设计,优化设计往往仅应用于简单部件,或沦为“设计优化”——在手动设计基本完成后在其基础上进行小幅度的优化改进。真正利用优化完成设计尚存在着不少障碍。其主要原因在于如下四方面的困难:
1) 首先是自动优化计算量的问题。一方面,传统快速分析方法适用范围狭小,在详细设计阶段的使用往往会给出误差较大的结果,甚至错误的规律,在非设计点的使用更是如此。因此优化设计往往被迫大量使用高精度计算方法,从而造成计算压力巨大。另一方面,由于现代飞机设计中部件间耦合作用不能忽略,单独部件优化获得的收益在全机中应用效果不佳(多点设计犹甚),因此往往需要基于全机模型进行分析,这使得计算量再次增加。如果进一步希望在耦合效应下进行全机优化,则设计变量急剧增加,计算量将远远超出能接受的范围。
2) 其次,优化问题目标与约束的合理定义较为复杂。以超临界机翼为例,当前气动设计需要考虑的因素有:巡航升阻比、升力系数、力矩、迎角等设计点性能;阻力发散、阻力蠕增、低速、抖振、99%M×L/D范围等非设计点指标;还有厚度、油箱容积、前缘装置、后缘装置、展向光滑性等几何约束;以及压力分布形态、失速起始位置、失速形态等其它方面的要求。这些设计点、非设计点特性要求大量引入时会导致计算量剧增,最优解难以评判,优化迭代难于收敛的问题。过多、过于细致、过为严苛的约束,容易造成优化始终难以产生符合约束的结果;而反之,则可能造成优化消耗大量的计算量在无意义的样本之上。
3) 第三,存在很多只可意会不可言传,难以数学表达的目标或约束。应该承认,设计存在一定的模糊的判断和决策的自由发挥之处。一些工程设计中必须要考虑的目标和约束过于复杂或没有数学定义,因而无法体现在优化之中,只能依靠人的观察和判断。比如超临界机翼的压力分布形态蕴含丰富的非设计点特性信息,常被设计师用来判断设计的优劣,但却很难严格、定量地描述。
4) 最后,自动优化收敛的走向和获得的结果常常不符合设计人员的经验,但设计师却无法干预。一些约束和目标是随着优化的进程才被设计人员意识到或发现需要进行控制。仍以超临界机翼为例,一般气动设计各指标的重要性难以硬性规定[85-86],如巡航升阻比、阻力发散特性和低速特性三项,设计师常常必须在优化到一定程度时暂时放松对某一个的要求以换取另两个的提升。有时,一些样本性能表现不佳但却蕴含着某种优秀的基因,但在自动优化下往往被不知不觉地淘汰。优化算法调用试算得到大量的结果和流场,也难以被设计人员学习利用形成经验和新的知识。
1.3 “人在回路”在当代气动优化设计中的引入以上这些困难导致目前尚难以完全依靠自动优化获得满足工程实际的设计,设计仍不能脱离设计人员,优化设计仍需要设计人员参与到优化设计准则的制定和优化循环的各个环节,将自己的经验和智慧与优化算法的搜索寻优能力相结合。“人在回路”应该是现阶段计算能力仍远不充足,优化准则尚不完备,人们对设计结果的综合评判仍缺乏理性手段的条件下,使优化设计满足工程设计需求的一种有效的解决方式。
Sobieszczanski于1997年就在综述文章[37]中指出:面向工程实际的优化方法需要引入“人机接口”以控制优化进程、引入判断与创新,其核心在于通过数据管理与可视化以及设计流程的自动化搭建,使设计师能够便捷地监控优化进程,再根据更新的输入重建优化进程,具体的工作详见综述[37]。进入21世纪,优化算法进一步发展,重建整个优化进程既浪费时间又浪费已有数据,因此“人”在优化设计中的作用发生了一定的调整[87]:一方面“人”可以减少随机搜索的无意义随机性;另一方面“人”需要监控优化过程,调整优化控制参数或调整种群个体以提高优化方法的有效性;而这就是现代“人在回路”思想的雏形。至此,优化设计从面向压力分布(反设计)、面向单一指标向面向综合性能、面向工程实际发展。“人”曾被研究者试图逐出“回路”,这一想法被证明过于激进,因此“人”又开始回归“回路”。
2 人在回路总体而言,“人在回路”的目的是要避免优化成为一个封闭的黑匣,更要避免优化成为一种数学游戏,而使其真正成为设计师的设计工具。狭义的“人在回路”指设计师在图 1的循环中实时监控和干预优化的过程与结果,如执行优化算法的切换、调节目标与约束的权重、干预个体和种群等[86]。而广义的“人在回路”更包含了设计师根据自己的经验对整个优化设计过程的设计与设定,如选择设计变量、定义目标、确定搜索空间、设定约束等。
2.1 优化目标与约束的设定在实际应用中,往往会发现型号设计的要求或目的是模糊的或概念性的(如鲁棒性),数学化难度较大,而应用优化方法需要目标的严格数学定义,因此设计师在参与优化设计时的一项主要工作就是利用对问题物理本质的理解和权衡,将模糊或难以实现的目标约束转化为可操作、可接受的形式,从而在现有优化方法中实现工程实践的种种要求。如鲁棒性、阻力蠕增、阻力发散、抖振、失速与升阻力特性等看似纷繁芜杂,需要大量的分析评估。但这些性能存在一定的规律,可以由少数特征状态的性能来分析推断。
2.1.1 面向性能的优化设定以超临界机翼设计为例,在优化巡航点效率时,对阻力蠕增、阻力发散特性的考量不必以近10倍的计算量获得Cd-Ma特性来评估,而可以通过适当的多点设计完成,如图 2中通过三点设计改善了机翼的阻力发散特性。
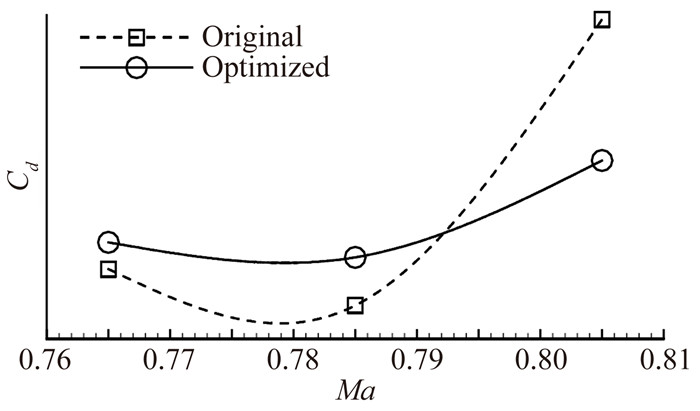
|
图 2 某窄体客机机翼优化前后阻力随马赫数变化曲线 Figure 2 Original and optimized wing drag-Mach curve of a certain single-aisle airplane |
多段翼型着陆构型的设计常常是追求最大升力系数的提升,但CFD无法直接预测失速迎角,也无法直接给出最大升力系数,硬性搜索最大升力系数的多点计算不但增加工作量,也囿于湍流模型难以准确。对此有经验的设计师会通过考查线性段升力系数和某一接近失速迎角工况的升力系数,以预测最大升力系数是否改善[85]。显然,这样的判断更容易在优化中实现数学定义,需要的计算量也更小。
约束方面,气动优化中最常用的约束有几何约束和性能约束两类,如由于结构、油箱容积等方面引发的最大厚度变化范围的限制[46, 65];为满足制造要求,尾缘厚度不得小于0.5%的要求[65];考虑气弹稳定性边界,最低可接受发散马赫数和颤振马赫数要大于1.5倍最高需求马赫数,各阶段结构件应力小于0.66667极限值的限制[42]等。几何约束往往出于结构考虑,但也包含对气动特性的支撑,如通过限制前缘半径下限以保持良好的低速特性;通过限制翼型最大弯度上限以保持良好的抖振特性[85];限制弦向10%位置厚度从而为前加载留余量并为前梁留结构空间;限制弦向80%厚度以保证后部厚度便于布置襟翼,并约束后加载强度以降低低头力矩等[87]。这些约束的设定似乎能够以模板的形式就某类问题固化下来,但实际上只有理解这些约束含义的设计师才明白哪些是不能越半步的雷池,哪些则可以放松一些。
2.1.2 面向流动的优化设定气动性能来自流动物理。如超临界性能的本质在于激波稳定性、激波边界层干扰、边界层分离等物理现象。这些物理现象难以在优化中用数学表达,但却能够被设计师所理解和掌握。设计师可面向流动的物理本质,或者根据流动结构来定义目标与约束。例如对抖振、低速鲁棒性的保证也可以通过少量特征状态的压力分布约束及优化实现[47, 86]。
对跨声速机翼而言,压力分布形态中蕴含十分丰富的信息,气动特性变化背后的物理规律往往可以在压力分布中有所体现。以阻力特性为例,在相同升力系数条件下翼型可能获得三种典型的压力分布形态(图 3从上至下依次为):近无激波(Shock Free)、双激波(Double Shock)和弱激波(Weak Shock),一般而言近无激波形态翼型弯度大,吸力平台低,升阻比较高但性能极不稳定;弱激波形态吸力平台高,激波靠前,升阻比相对较低但阻力发散最好;双激波为二者的过渡形态,阻力发散特性居中。文献[85]中对三种形态的阻力发散、鲁棒性等特性(图 4)进行详细研究后,认为激波位置适当靠前的弱激波形态是窄体客机较为合理的超临界翼型压力分布,并依此定义了相应的压力分布约束,引导优化演进向这种类型的压力分布形态发展,取得了较好效果。
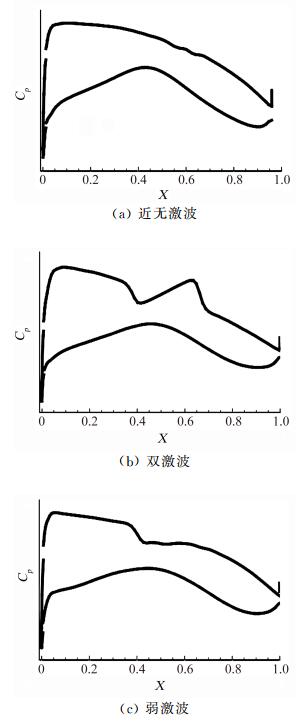
|
图 3 三种压力分布形态 Figure 3 Three kinds of Cp distribution |
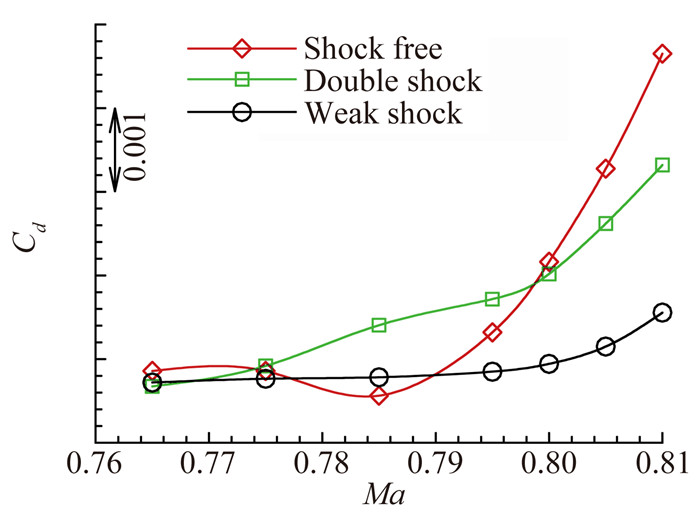
|
图 4 三种压力分布形态的阻力变化趋势 Figure 4 Drag-Mach curves of the three kinds of Cp distribution |
事实上经过人们长时间的研究,超临界机翼的压力分布形态早已形成了弱激波形态的定势,而这种形态决定了这种机翼在升力获取、激波阻力、激波稳定性、后缘分离特性、结构容积等方面达到了一个较好的折衷状态。对压力分布形态的掌控也是设计师的主要工作,图 5中引用文献[85]对某型窄体客机机翼优化的压力分布形态约束,体现了设计师对优化设计的参与和主导,也体现了多年来人们在超临界机翼设计中的认识积累:
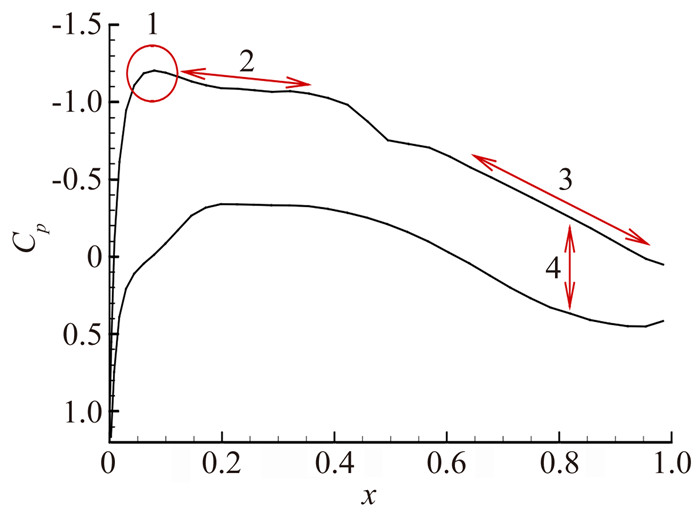
|
图 5 某型窄体客机机翼翼型压力分布约束示意图 Figure 5 Cp constraints of a certain single-aisle airplane wing's foil |
1) 吸力峰值不能低于-1.2,以避免前缘加速过快向“尖峰”翼型发展;
2) 负压平台区(0.08 < x < 0.5) 圧力曲线斜率在-0.2到0.5之间,以保证平台长度;
3) 压力恢复区(0.6 < x < 1.0) 圧力曲线斜率小于3,以避免流动分离;
4) 后加载约束上下表面压力差,以限制低头力矩。
压力分布形态约束很难有普适的范式可循。例如某型宽体客机的合理压力分布形态与窄体客机发生了很大的变化(图 6,从上至下依次为巡航设计点、低升力系数设计点和阻力发散设计点的翼型压力分布约束),约束根据相应工况和目标的变化进行调整[85],并增加了非设计点的约束:
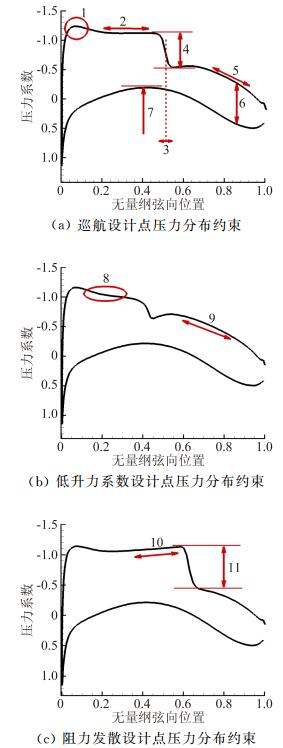
|
图 6 某型宽体客机机翼翼型压力分布约束示意图 Figure 6 Cp constraints of a certain dual-aisle airplane wing's foil |
1) 低升力系数点——由于激波位置靠后,容易出现吸力平台塌陷、双激波等现象从而造成抖振、低升力性能恶化,因此引入吸力平台梯度约束和压力恢复约束;
2) 阻力发散点——由于来流马赫数大,巡航点激波位置靠后使得激波在马赫增加时更易进一步增强,因此设置阻力发散点压力分布的吸力平台梯度约束和激波强度约束。
图 7(a)给出了优化过程大范围探索的演化过程(横坐标为巡航设计点阻力系数,纵坐标为阻力发散设计点阻力系数;黄色为不符合约束条件的个体,黑色为符合约束条件的个体),可以看出,约束条件淘汰了压力分布形态与期望形态符合欠佳的个体,引导优化更高效地向综合最优的方向进行,最终如图 7(b)所示形成了Pareto前缘,给出了选择最优个体的参考依据。
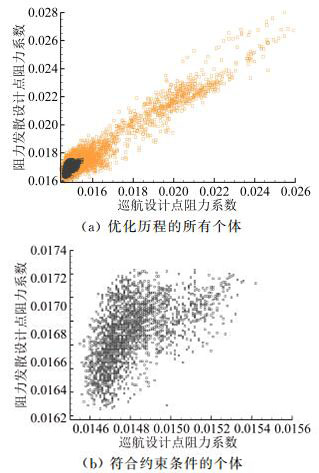
|
图 7 某型宽体客机机翼初步优化的Pareto前缘 Figure 7 Initial optimization's pareto front of a certain dual-aisle airplane wing |
图 8的九个图分别代表沿机翼展向从翼根到翼梢(10%到90%)不同截面的压力分布(红色:优化方案,黑色:初始方案),可看出在外翼段,由于压力分布形态约束的施加,激波位置向翼型前缘移动到了弦长的55%左右,而激波强度也明显减弱,优化获得了满意的效果。

|
图 8 初步优化的优化个体巡航状态压力分布与初始机翼对比 Figure 8 Cp distributioncomparison of original (black) and optimized (red) wing |
优化方法确定后,并不意味着优化就可以无监管地进行了,优化进程控制是保证优化效率、优化有效性的重要环节,也是设计师引导优化方向,体现不便于数学表达的目标和约束,实现设计意志的手段。设计师对优化进程的控制首先需要对优化进程和已产生数据进行分析,得到当前状态的评估[37],之后由人调整优化方向、优化方法和约束,并对最终结果进行评估与选择。
在无法保证严格全局搜索的情况下,为避免“无意义的随机性”,调整优化进程向有希望的方向搜索是明智且有效的[87]。应用遗传算法进行的优化中一种简单有效的做法就是种群调控,如采取精英策略[88],或根据某种评估(根据流动形态人工干预[47];利用代理模型评估、预测优秀个体[89-90])添加新个体引导种群进化方向;也可以通过调整进化过程,如将基因组交叉互换过程的随机操作用博弈理论指导的最优组合确定方法替代以提高效率[91];还可以调节多目标加权的权重以调整方向[21]。其他优化方法如变参数方法通过调整算法中的控制参数,调整子代的演化方向依赖于父代种群的程度,以改变方向并同时调整算法的鲁棒性和效率[92];多目标禁忌搜索[93],和其它改进策略如并行、多样性保持、多重复杂度的函数评估方法[94]等也得到了研究发展。
除却上述优化算法层面的实时调整,设计师也可根据自己的经验对遗传种群进行个体操作,如对“无意义个体”进行剔除和替换。文献[85-86]基于进化算法,通过对种群个体和目标、约束、优化算法的调整实现研究人员对优化进程的调控,引导优化根据设计者经验和设计思想高效发展。其中针对遗传种群个体的操作包括:人工删除个体、人工引入新个体、人工修改个体(人工修型接口)、人工结果选择四个方面。删除一些已知的不利个体避免了无意义搜索;引入新个体可以引入外来基因,增强种群的多样性,也可体现研究人员对某一方面问题可能解决方案的思考与尝试;人工个体选择(如图 9)体现了研究人员对各性能之间的权衡,一些表现好的个体,因其与其它个体相似度太高,或因其压力分布形态太差等原因而被淘汰。一些性能很差,但具有某方面有利特点(如前缘半径大,有利于缝翼布置),或有新意的个体(如压力分布新形态)可能被保留甚至加强。人工修型接口(如图 10)使得优化可以继承传统试凑法设计的优势,更为直接地引入设计师的操作,从而实现人工修型设计与自动优化的有机结合。如图 11所示,研究人员首先进行全局搜索,之后对Pareto前缘附近的个体进行评估分析,并在考虑低速特性进行下表面前缘人工修型后,引回种群,继续优化。最终获得了满意的方案。
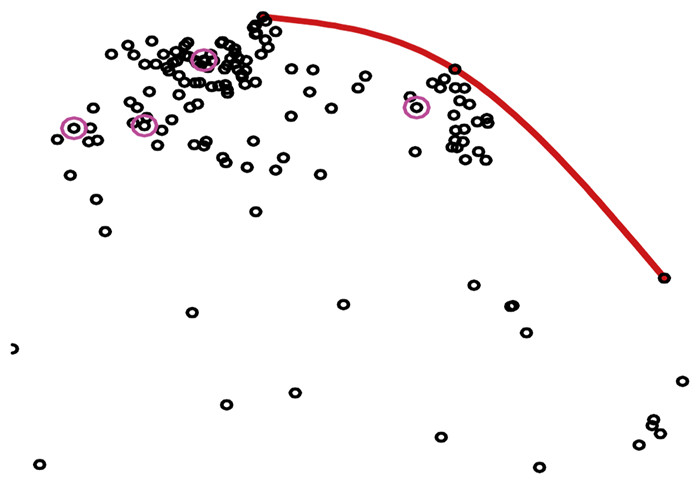
|
图 9 根据Pareto前沿进行人工结果选择 Figure 9 Manually individual selection based on Pareto front |
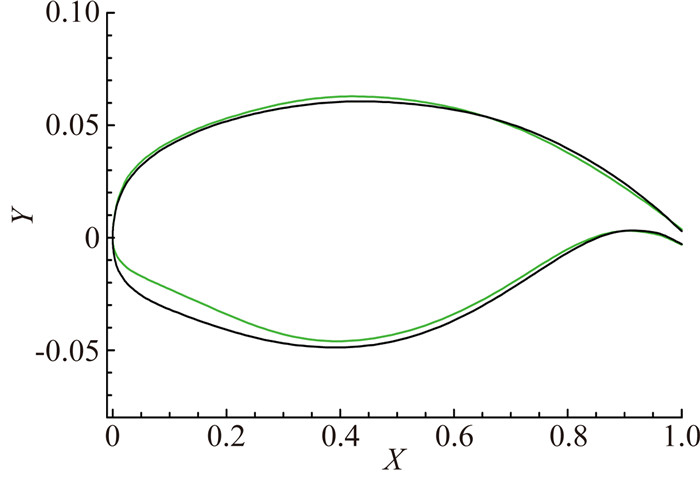
|
图 10 人工修型,返回优化流程 Figure 10 Manually design then add into optimization |
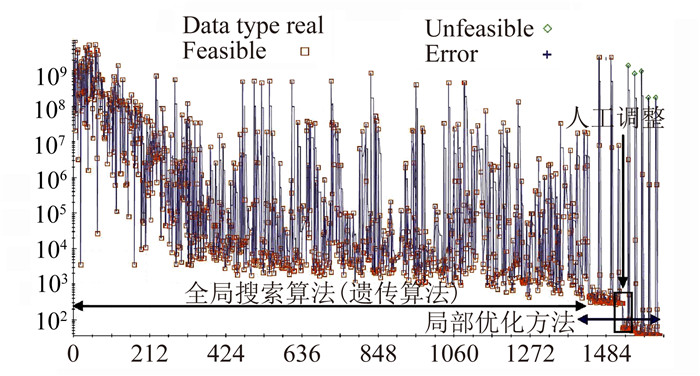
|
图 11 优化方法切换与人工修型的引入 Figure 11 The switch of optimization methods and the introduction of manually adjustment |
现有的优化算法在寻优的广度和深度上存在一定的矛盾。如进化类算法具有全局搜索的优势,但收敛较慢;梯度类算法则收敛较快,但容易收敛到局部最优解。设计师可以监控优化进程,适时切换或调整寻优算法,一种典型的思路为:先在大范围内用大数目的测试点进行搜索或重构,捕捉可能存在全局最优的空间,当搜索空间被缩小至可接受的程度时,使用高效率、高精度的优化方法得到最优解。需要注意的是,广度、深度的平衡直接影响了优化的速度和寻优效果,切换的时机需要仔细权衡。而且不同的优化方法在同一问题上的表现也是不同的,如文献[30]对比了三种优化方法在高速民机优化中的差异,文献[95]对比了遗传算法和梯度算法在多目标优化中的表现,文献[41]对比了遗传算法、梯度算法和基于kriging的优化方法,认为后者非常适用于少变量、多目标的优化问题。问题的多尺度性和方法的多样性使得研究者需要根据问题合理选择优化方法,以获得速度与精度、全局与局部的平衡。在遗传算法中调整种群也可以影响深度和广度的平衡[96];也可以构造复杂的适应函数,通过调整参数控制平衡[27]。还有一些研究通过一些多准则决策方法帮助优化快速逼近真实帕雷托前缘[64],自适应范围的遗传算法目前也有较多发展[97-101]。
在优化过程中,设计师对约束和目标权重的实时调整也是一种重要的“人在回路”的手段。优化之初,过多的约束使得遗传算法产生的有效样本很少。此时,设计师通过非支配排序中的调整放松甚至关闭了部分约束。在优化进入正轨、种群得以建立后再逐渐调节到约束的正常工作状态。对压力分布形态的约束也需要根据设计师在优化过程中的分析、思考和积累进行不断的调整,约束体系中激波位置、后加载强度等一般无法在优化设计之初就十分合理地定义,需要在优化进程中多次修改才达到理想的状态。另一方面,优化过程中可能出现优化结果始终无法满足约束的情况,说明优化过程没能向满足约束的方向发展,此时可以通过将约束设置为目标来引导种群向可行的方向演化,在种群内有足够个体满足约束后,将该目标重新切换为约束,使优化正常进行。
优化收敛之后,多目标问题往往得到帕雷托前缘,设计师可以从中选择各项性能较均匀、流动结构和几何较合理的结果作为最终设计,此时需要设计师丰富的经验作为最终评判标准,当然选择也存在设计师偏好和个性的因素。不过当决定并不十分清晰时,也可以使用一些决策方法如“Fuzzy Bellman Zedah”来辅助人来选择[65]。事实上,不只是对结果的选择。设计师“人在回路”中调控行为的决策基于经验理解,也依赖于对当前优化状态的判断。一些分析手段可以帮助设计师得到有助于做出更明智调整[41, 102],如文献[41]通过推阻分解和相关度分析手段得到了各阻力部分与小翼设计变量的相关关系,从而使优化集中调整相关的变量,加快了收敛速度。
2.3 “人在回路”的实施要求图 12展示了“人在回路”在优化回路中的引入和实现环节,“人在回路”优化设计的实现需要优化方法和设计师共同做出努力。也就是说从优化方法而言,要便于设计师参与到循环中进行调控。而设计师也应该理解优化方法的原理、逻辑和流程,并尽量将自己的经验和灵感转化为优化方法的设定和调整。
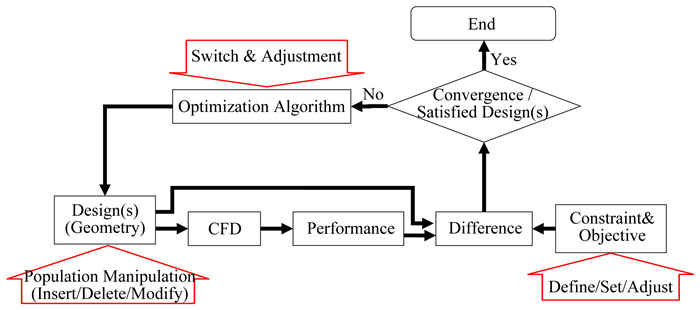
|
图 12 优化回路中“人在回路”的引入 Figure 12 "Man-in-loop" in optimization design |
在优化方法选择和优化平台搭建中,有以下几点需要注意:1) 根据“人在回路”的要求,选择便于人参与调控的优化方法。比如启发式搜索(如遗传算法)在全局搜索和多目标优化方面具有优势的同时也存在搜索随机性有时过强、局部收敛缓慢的劣势,但它容易通过种群调控和个体操作实现“人在回路”;而共轭算法虽然局部收敛能力强大,但调控略有难度,不过近年来也有人研究“人在回路”的办法[103-106];2) 设置方便人在回路的接口。如上面提到的优化准则设定,寻优算法参数调节、种群调控、个体操作、结果筛选、约束与目标调整、寻优方法切换的实时开展等,都应该提供接口允许设计师进行方便的操作;也可以使用先进的几何造型方法使个体修改与引入、人工修型等变得更加灵活;3) 设置决策辅助功能,如帕累托前缘分析、种群的统计归纳分析、灵活的个体查看与分析等功能;4) 还有就是需要使优化回路的速度与节奏适应设计师的工作习惯与承受能力,例如部署并行计算能力,实现“一日设计循环”[85],使设计师能够有充分时间分析结果,参与优化设计的同时又不至于降低优化设计的效率。
对设计师而言,应该认识到并承认人工经验与优化算法作为设计工具的优势与不足,理解优化算法的运作方式,掌握优化平台可设定与可调节之处,在优化过程中不断观察、学习和思考,处理好优化自主演进和“人在回路”调控之间的度,并努力将自身经验与创意转化为优化方法能够接收、处理的表达形式。
3 “人在回路”的进一步发展目前“人在回路”可以通过优化的设定和优化进程中的实时调整,弥补现有计算能力与优化算法仍不能支持完全自动化的全面寻优的不足。但人毕竟有其局限:人的经验、记忆力有限;人对强耦合、强非线性问题的理解、梳理能力有限;人无法像计算机那样不眠不休等。随着大规模并行计算能力的发展、问题复杂程度的增加,人在“人在回路”的优化设计中又将成为瓶颈,随着人工智能、深度学习等的飞速发展,引入机器智能来辅助甚至代替设计师在“人在回路”中的行为成为人们思考的方向。
总体而言,近期迅速发展的人工神经网络、代理模型等方法在信息收纳和响应重构方面体现出了存储量大,映射多尺度、非线性构建能力强的优势。深度学习与数据挖掘中的一些手段也表现出了强大的分析能力,并已出现了人工智能应用于优化的一些实践[107-110]。但本文讨论的人工智能终究是为了模拟“人在回路”时,设计师在参与和监控优化设计中表现出的两种特征行为(“归纳性行为”和“演绎性行为”)和两种特征思想(“面向性能”和“面向流场”),因而此时人工智能的应用思想相对复杂一些。
人工智能的引入最初是将优化与人工神经网络等混合形成对优化算法的增强,可实现优化能力和可调控性的大幅提高。比如代理模型、人工神经网络等的发展使得优化过程中产生并分析的大量样本可被充分利用,替代或部分替代CFD分析;通过人工神经网络[111-112]和代理模型[113-116]可实现不同置信度[117-120]的数据模型构建与整合[121, 123],以及梯度信息的利用[124-126]等。
近期开发出的众多方法能够进一步辅助甚至替代“人在回路”中的分析与调控作用,如敏感度分析[127]等手段使得对优化进程的评估变得更加直观有效。实际问题中并非所有的设计变量都对性能有显著影响,基于数据挖掘的相关度分析(ANOVA)可以实现变量影响显著性评估,甚至可以分析较优个体间共性和设计变量、性能参数之间的关系[41, 128],得到其中关联或影响的显式表达[129],从而指导优化并提高效率。类似的还有数据挖掘中的自组织数据挖掘算法(SOM)、粗糙集理论(rough set theory)、决策树分析[57]等可以帮助缩并设计变量或设计目标[130],从而提高优化效率。一些优化算法的自动切换策略[131],和自适应参数调整策略[132]也能够取代设计师的部分“人在回路”行为。
目前看来,基于人工神经网络、代理模型的多类信息利用和基于数据挖掘、深度学习的知识构建与决策是模拟设计师“人在回路”行为的解决之道。目前的尝试大多集中于前者,一般利用各类数学工具对已完成算例进行蕴含规律的总结归纳和简单的结果预测。但依据这些规律分析优化演进方向、调整优化策略的“演绎性行为”实现仍有困难。人工智能对流动结构的分析和对流体力学知识的运用还远不能达到人的水平,因此在很多方面还无法代替人。但无论如何,人们已经开始尝试从“人在回路”向“机器人在回路”的方向发展。
4 结论与展望优化方法应用于工程设计中至今已近40年,“人”在优化设计中经历了“出回路-进回路-出回路”的历程,反映出气动设计/优化方法/计算能力共同发展进步过程中出现的不均衡和不满足的矛盾。在现阶段“人在回路”仍是解决优化方法满足气动设计工程需求的一个有效、有益的解决办法。
优化方法在工程设计实践中,应明确其工具属性。在现阶段及可预见的将来,工程问题的复杂性和庞大性使得设计过程中既迫切需要优化算法将设计师从相对简单的重复性工作中释放出来,又离不开人的分析、判断、调控。一个成功的设计应该充分发挥人的智慧和机器的强大计算能力,既不使人的时间浪费于简单重复工作,也不使强大的计算机等待人的操作或被人限制与干扰。而这需要设计师和优化方法研究者的共同努力。
人在未来设计中该如何发挥作用,仍有待思考和研究。未来的设计中人会不会、应不应该被计算机完全取代,这其实是人工智能发展的普遍性、哲学性问题。但减少人的重复、机械工作量,使其能够集中于创造性的工作应该是明确的主题。
| [1] |
Sobieszczanski-Sobieski J, Morris A, et al. Multidisciplinary design optimization supported by knowledge basedengineering[M]. John Wiley & Sons, 2015.
(  0) 0) |
| [2] |
Malone B, Mason W H. Multidisciplinary optimization in aircraft design using analytic technologymodels[J]. Journal of Aircraft, 1995, 32(2): 431-438. DOI:10.2514/3.46734 (  0) 0) |
| [3] |
Hess J T, Smith A M. Calculation of nonlifting potential flow about arbitrary three dimensional bodies[J]. Journal of Ship Research, 1964, 8(2): 22-24. (  0) 0) |
| [4] |
Tinoco E N, Ball D N, Rice F A. PAN AIR analysis of a transport high-lift configuration[J]. Journal of Aircraft, 1987, 24(3): 181-187. DOI:10.2514/3.45414 (  0) 0) |
| [5] |
Chen A W, Tinoco E N. PAN AIR applications to aero-propulsionintegration[J]. Journal of Aircraft, 1984, 21(3): 161-167. DOI:10.2514/3.48241 (  0) 0) |
| [6] |
Katz J, Plotkin A. Low-speed aerodynamics[M]. Cambridge University Press, 2001.
(  0) 0) |
| [7] |
Melin T. A vortex lattice MATLAB implementation for linear aerodynamic wing applications[D]. Master's Thesis, Department of Aeronautics, Royal Institute of Technology (KTH), Stockholm, Sweden, 2000. https://link.springer.com/content/pdf/10.1007%2Fs13272-015-0174-z.pdf
(  0) 0) |
| [8] |
Amadori K, Melin T, Krus P. Multidisciplinary optimization of wing structure using parametric models[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. 2013:140.
(  0) 0) |
| [9] |
Labrujere T E, Slooff J W. Computational methods for the aerodynamic design of aircraft components[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 183-214. DOI:10.1146/annurev.fl.25.010193.001151 (  0) 0) |
| [10] |
Chattopadhyay A, Narayan J R. Optimum design of high speed prop-rotors using a multidisciplinary approach[J]. Engineering Optimization, 1993, 22(1): 1-17. DOI:10.1080/03052159308941322 (  0) 0) |
| [11] |
Malone J B, Narramore J C, Sankar L N. Airfoil design method using the Navier-Stokes equations[J]. Journal of Aircraft, 1991, 28(3): 216-224. DOI:10.2514/3.46015 (  0) 0) |
| [12] |
Garabedian P, Mcfadden G. Design of supercritical swept wings[J]. AIAA Journal, 1982, 20(3): 289-291. DOI:10.2514/3.7912 (  0) 0) |
| [13] |
Malone J, Vadyak J, Sankar L. A technique for the inverse aerodynamic design of nacelles and wing configurations[C]//3rd Applied Aerodynamics Conference. 1985:4096.
(  0) 0) |
| [14] |
Malone J B, Vadyak J, Sankar L N. Inverse aerodynamic design method for aircraft components[J]. Journal of Aircraft, 1987, 24(1): 8-9. DOI:10.2514/3.45403 (  0) 0) |
| [15] |
Bell R A, Cedar R D. An inverse method for the aerodynamic design of three-dimensional aircraft engine nacelles[R]. NASA Report, 1991.
(  0) 0) |
| [16] |
Dulikravich G. Shape inverse design and optimization for three-dimensional aerodynamics[C]//33rd Aerospace Sciences Meeting and Exhibit. 1995:695.
(  0) 0) |
| [17] |
Dang T, Isgro V. Euler-based inverse method for turbomachine blades. Ⅰ-Two-dimensional cascades[J]. AIAA Journal, 1995, 33(12): 2309-2315. DOI:10.2514/3.12985 (  0) 0) |
| [18] |
Vanegmond J. Numerical optimization of target pressure distributions for subsonic and transonic airfoil design[R]. AGARD N 90-2097614-05, 1990.
(  0) 0) |
| [19] |
Kim H J, Rho O H. Dual-point design of transonic airfoils using the hybrid inverse optimization method[J]. Journal of Aircraft, 1997, 34(5): 612-618. DOI:10.2514/2.2237 (  0) 0) |
| [20] |
Obayashi S, Takanashi S. Genetic algorithm for aerodynamic inverse optimization problems[C]//Genetic Algorithms in Engineering Systems:Innovations and Applications, 1995. GALESIA. First International Conference on (Conf. Publ. No. 414). IET, 1995:7-12. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=501639
(  0) 0) |
| [21] |
Obayashi S, Takanashi S. Genetic optimization of target pressure distributions for inverse design methods[J]. AIAA Journal, 1996, 34(5): 881-886. DOI:10.2514/3.13163 (  0) 0) |
| [22] |
Obayashi S. Aerodynamic optimization with evolutionary algorithms[C]//Control'96, UKACC International Conference on (Conf. Publ. No. 427), IET, 1996:687-692
(  0) 0) |
| [23] |
Kim H J, Rho O H. Aerodynamic design of transonic wings using the target pressure optimization approach[J]. Journal of Aircraft, 1998, 35(5): 671-677. DOI:10.2514/2.2374 (  0) 0) |
| [24] |
Harris C D. NASA Supercritical airfoils:a matrix of family-related airfoils[R]. NASA Report, 1990.
(  0) 0) |
| [25] |
Quagliarella D, Della Cioppa A. Genetic algorithms applied to the aerodynamic design of transonic airfoils[J]. Journal of Aircraft, 1995, 32(4): 889-891. DOI:10.2514/3.46810 (  0) 0) |
| [26] |
Vicini A, Quagliarella D. Airfoil and wing design through hybrid optimization strategies[J]. AIAA Journal, 1999, 37(5): 634-641. DOI:10.2514/2.764 (  0) 0) |
| [27] |
Fan H Y, Xi G, Wang S J. A dual fitness function genetic algorithm and application in aerodynamic inverse design[J]. Inverse Problems in Engineering, 2000, 8(4): 325-344. DOI:10.1080/174159700088027734 (  0) 0) |
| [28] |
Jones B R, Crossley W A, Lyrintzis A S. Aerodynamic and aeroacoustic optimization of rotorcraft airfoils via a parallel genetic algorithm[J]. Journal of Aircraft, 2000, 37(6): 1088-1096. DOI:10.2514/2.2717 (  0) 0) |
| [29] |
Marco N, Lanteri S. A two-level parallelization strategy for genetic algorithms applied to optimum shape design[J]. Parallel Computing, 2000, 26(4): 377-397. DOI:10.1016/S0167-8191(99)00116-7 (  0) 0) |
| [30] |
Cox S E, Haftka R T, Baker C A, et al. A comparison of global optimization methods for the design of a high-speed civil transport[J]. Journal of Global Optimization, 2001, 21(4): 415-432. DOI:10.1023/A:1012782825166 (  0) 0) |
| [31] |
Lim D, Ong Y S, Jin Y, et al. Efficient hierarchical parallel genetic algorithms using grid computing[J]. Future Generation Computer Systems, 2007, 23(4): 658-670. DOI:10.1016/j.future.2006.10.008 (  0) 0) |
| [32] |
Asouti V G, Giannakoglou K C. Aerodynamic optimization using a parallel asynchronous evolutionary algorithm controlled by strongly interacting demes[J]. Engineering Optimization, 2009, 41(3): 241-257. DOI:10.1080/03052150802415665 (  0) 0) |
| [33] |
Bharti S, Frecker M, Lesieutre G. Optimal morphing-wing design using parallel nondominated sorting genetic algorithm Ⅱ[J]. AIAA Journal, 2009, 47(7): 1627-1634. DOI:10.2514/1.36003 (  0) 0) |
| [34] |
Ebrahimi M, Jahangirian A. A hierarchical parallel strategy for aerodynamic shape optimization with genetic algorithm[J]. Scientia Iranica. Transaction D, Computer Science & Engineering, Electrical, 2015, 22(6): 2379. (  0) 0) |
| [35] |
Hutchison M G, Unger E R, Mason W H, et al. Variable-complexity aerodynamic optimization of a high-speed civil transport wing[J]. Journal of Aircraft, 1994, 31(1): 110-116. DOI:10.2514/3.46462 (  0) 0) |
| [36] |
Sobieszczanski-Sobieski J. Multidisciplinary design optimization:an emerging new engineering discipline[M]//Advances in Structural Optimization. Springer Netherlands, 1995:483-496.
(  0) 0) |
| [37] |
Sobieszczanski-Sobieski J, Haftka R T. Multidisciplinary aerospace design optimization:survey of recent developments[J]. Structural Optimization, 1997, 14(1): 1-23. DOI:10.1007/BF01197554 (  0) 0) |
| [38] |
Toivanen J, Makinen R E, Périaux J, et al. Multidisciplinary shape optimization in aerodynamics and electromagnetics using genetic algorithms[J]. Intl J. Numer. Meth. Fluids, 1999, 30: 149-159. DOI:10.1002/(ISSN)1097-0363 (  0) 0) |
| [39] |
Kim Y, Jeon Y H, Lee D H. Multi-objective and multidisciplinary design optimization of supersonic fighter wing[J]. Journal of Aircraft, 2006, 43(3): 817-824. DOI:10.2514/1.13864 (  0) 0) |
| [40] |
Chiba K, Oyama A, Obayashi S, et al. Multidisciplinary design optimization and data mining for transonic regional-jet wing[J]. Journal of Aircraft, 2007, 44(4): 1100-1112. DOI:10.2514/1.17549 (  0) 0) |
| [41] |
Takenaka K, Hatanaka K, Yamazaki W, et al. Multidisciplinary design exploration for a winglet[J]. Journal of Aircraft, 2008, 45(5): 1601-1611. DOI:10.2514/1.33031 (  0) 0) |
| [42] |
Berci M, Toropov V V, Hewson R W, et al. Multidisciplinary multifidelity optimisation of a flexible wing aerofoil with reference to a small UAV[J]. Structural and Multidisciplinary Optimization, 2014, 50(4): 683-699. DOI:10.1007/s00158-014-1066-2 (  0) 0) |
| [43] |
Cliff S E, Reuther J J, Saunders D A, et al. Single-point and multipoint aerodynamic shape optimization of high-speed civil transport[J]. Journal of Aircraft, 2001, 38(6): 997-1005. DOI:10.2514/2.2886 (  0) 0) |
| [44] |
Kim H J, Rho O H. Dual-point design of transonic airfoils using the hybrid inverse optimization method[J]. Journal of Aircraft, 1997, 34(5): 612-618. DOI:10.2514/2.2237 (  0) 0) |
| [45] |
Kim H J, Kim C, Rho O H. Multipoint inverse design method for transonic wings[J]. Journal of Aircraft, 1999, 36(6): 941-947. DOI:10.2514/2.2555 (  0) 0) |
| [46] |
Peigin S, Epstein B. Multipoint aerodynamic design of wing-body configurations for minimum drag[J]. Journal of Aircraft, 2007, 44(3): 971-980. DOI:10.2514/1.26746 (  0) 0) |
| [47] |
Tian Y, Liu P Q, Li Z. Multi-objective optimization of shock control bump on a supercritical wing[J]. Science China Technological Sciences, 2014, 57(1): 192-202. DOI:10.1007/s11431-013-5410-3 (  0) 0) |
| [48] |
Nemec M, Zingg D W, Pulliam T H. Multipoint and multi-objective aerodynamic shape optimization[J]. AIAA Journal, 2004, 42(6): 1057-1065. DOI:10.2514/1.10415 (  0) 0) |
| [49] |
Pierret S, Filomeno Coelho R, Kato H. Multidisciplinary and multiple operating points shape optimization of three-dimensional compressor blades[J]. Structural and Multidisciplinary Optimization, 2007, 33(1): 61-70. (  0) 0) |
| [50] |
Ju Y P, Zhang C H. Multi-point robust design optimization of wind turbine airfoil under geometric uncertainty[J]. Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2012, 226(2): 245-261. DOI:10.1177/0957650911426540 (  0) 0) |
| [51] |
Ju Y P, Zhang C H. Multi-point and multi-objective optimization design method for industrial axial compressor cascades[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2011, 225(6): 1481-1493. DOI:10.1177/0954406210395878 (  0) 0) |
| [52] |
Vicini A, Quagliarella D. Inverse and direct airfoil design using a multiobjective genetic algorithm[J]. AIAA Journal, 1997, 35(9): 1499-1505. DOI:10.2514/2.274 (  0) 0) |
| [53] |
Takahashi S, Obayashi S, Nakahashi K. Inverse design optimization of transonic wings based on multi-objective genetic algorithms[J]. AIAA Journal, 1999, 37(12): 1656-1662. DOI:10.2514/2.648 (  0) 0) |
| [54] |
Wang J F, Periaux J, Sefrioui M. Parallel evolutionary algorithms for optimization problems in aerospace engineering[J]. Journal of Computational and Applied Mathematics, 2002, 149(1): 155-169. DOI:10.1016/S0377-0427(02)00527-7 (  0) 0) |
| [55] |
Benini E. Three-dimensional multi-objective design optimization of a transonic compressor rotor[J]. Journal of Propulsion and Power, 2004, 20(3): 559-565. DOI:10.2514/1.2703 (  0) 0) |
| [56] |
Park K, Lee J. Optimal design of two-dimensional wings in ground effect using multi-objective genetic algorithm[J]. Ocean Engineering, 2010, 37(10): 902-912. DOI:10.1016/j.oceaneng.2010.03.001 (  0) 0) |
| [57] |
Sugimura K, Obayashi S, Jeong S. Multi-objective optimization and design rule mining for an aerodynamically efficient and stable centrifugal impeller with a vaned diffuser[J]. Engineering Optimization, 2010, 42(3): 271-293. DOI:10.1080/03052150903171084 (  0) 0) |
| [58] |
ÖksüzÖ, AkmandorS. Multi-objective aerodynamic optimization of axial turbine blades using a novel multilevel genetic algorithm[J]. Journal of Turbomachinery, 2010, 132(4): 041009. (  0) 0) |
| [59] |
Stadler W. Multicriteria optimization in engineering and in the sciences[M]. Springer Science & Business Media, 2013.
(  0) 0) |
| [60] |
Périaux J, Chen H Q, Mantel B, et al. Combining game theory and genetic algorithms with application to DDM-nozzle optimization problems[J]. Finite Elements in Analysis and Design, 2001, 37(5): 417-429. DOI:10.1016/S0168-874X(00)00055-X (  0) 0) |
| [61] |
Schaer J D. Multiple objective optimization with vector evaluated genetic algorithms[C]//Sixth International Conference on Genetic Algorithms, Morgan Kaufmann, San Mateo, CA, 1985, 93-100.
(  0) 0) |
| [62] |
Goldberg D E, Holland J H. Genetic algorithms and machine learning[J]. Machine learning, 1988, 3(2): 95-99. (  0) 0) |
| [63] |
Deb K, Agrawal S, Pratap A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization:NSGA-Ⅱ[C]//International Conference on Parallel Problem Solving From Nature. Springer Berlin Heidelberg, 2000:849-858.
(  0) 0) |
| [64] |
Wang X D, Hirsch C, Kang S, et al. Multi-objective optimization of turbomachinery using improved NSGA-Ⅱ and approximation model[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(9): 883-895. (  0) 0) |
| [65] |
Sanaye S, Hassanzadeh A. Multi-objective optimization of airfoil shape for efficiency improvement and noise reduction in small wind turbines[J]. Journal of Renewable and Sustainable Energy, 2014, 6(5): 053105. DOI:10.1063/1.4895528 (  0) 0) |
| [66] |
Da Ronco C C, Ponza R, Benini E. Aerodynamic shape optimization of aircraft components using an advanced multi-objective evolutionary approach[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 285: 255-290. DOI:10.1016/j.cma.2014.10.024 (  0) 0) |
| [67] |
Fonseca C M, Fleming P J. An overview of evolutionary algorithms in multiobjective optimization[J]. Evolutionary Computation, 1995, 3(1): 1-16. DOI:10.1162/evco.1995.3.1.1 (  0) 0) |
| [68] |
Phadke M S. Quality engineering using robust design[M]. Prentice Hall PTR, 1995.
(  0) 0) |
| [69] |
Kumar A, Keane A J, Nair P B, et al. Robust design of compressor fan blades against erosion[J]. Journal of Mechanical Design, 2006, 128(4): 864-873. DOI:10.1115/1.2202886 (  0) 0) |
| [70] |
Yao W, Chen X, Luo W, et al. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles[J]. Progress in Aerospace Sciences, 2011, 47(6): 450-479. DOI:10.1016/j.paerosci.2011.05.001 (  0) 0) |
| [71] |
Noor A K. Nondeterministic approaches and their potential for future aerospace systems[R]. NASA Report, 2001.
(  0) 0) |
| [72] |
Epstein B, Peigin S. Robust hybrid approach to multiobjective constrained optimization in aerodynamics[J]. AIAA Journal, 2004, 42(8): 1572-1581. DOI:10.2514/1.992 (  0) 0) |
| [73] |
Peigin S, Epstein B. Robust handling of non-linear constraints for GA optimization of aerodynamic shapes[J]. International Journal for Numerical Methods in Fluids, 2004, 45(12): 1339-1362. DOI:10.1002/(ISSN)1097-0363 (  0) 0) |
| [74] |
Taguchi G, Wu Y. Introduction to off-line quality control[R]. Central Japan Quality Control Association, Nagoya, Japan, 1980.
(  0) 0) |
| [75] |
Nair V N, Abraham B, Mackay J, et al. Taguchi's parameter design:a panel discussion[J]. Technometrics, 1992, 34(2): 127-161. DOI:10.1080/00401706.1992.10484904 (  0) 0) |
| [76] |
Trosset M W. Taguchi and robust design[R]. Technical Report No. 96-31, Houston, TX., 1996
(  0) 0) |
| [77] |
Box G. Signal-to-noise ratios, performance criteria, and transformations[J]. Technometrics, 1988, 30(1): 1-17. DOI:10.1080/00401706.1988.10488313 (  0) 0) |
| [78] |
Trosset M W, Alexandrov N M, Watson L T. New methods for robust design using computer simulations[C]//American Statistical Association, 2003, Proceedings of the Section on Physical and Engineering Science.
(  0) 0) |
| [79] |
Welch W, Yu T, Kang S M, et al. Computer experiments for quality control by parameter design[J]. Journal of Quality Technology, 1990, 22(1): 15-22. (  0) 0) |
| [80] |
Welch W J, Sacks J. A system for quality improvement via computer experiments[J]. Communications in Statistics-Theory and Methods, 1991, 20(2): 477-495. DOI:10.1080/03610929108830510 (  0) 0) |
| [81] |
Ben-Tal A, Nemirovski A. Robust truss topology design via semidefinite programming[J]. SIAM Journal on Optimization, 1997, 7(4): 991-1016. DOI:10.1137/S1052623495291951 (  0) 0) |
| [82] |
Gunawan S, Azarm S. Non-gradient based parameter sensitivity estimation for single objective robust design optimization[J]. Journal of Mechanical Design, 2004, 126(3): 395-402. DOI:10.1115/1.1711821 (  0) 0) |
| [83] |
Lewis R M, Huyse L. Aerodynamic shape optimization of two-dimensional airfoils under uncertain conditions[R]. Institute for Computer Applications in Science and Engineering Hampton Va, 2001.
(  0) 0) |
| [84] |
Li W, Huyse L, Padula S. Robust airfoil optimization to achieve drag reduction over a range of mach numbers[J]. Structural and Multidisciplinary Optimization, 2002, 24(1): 38-50. DOI:10.1007/s00158-002-0212-4 (  0) 0) |
| [85] |
Zhang Y F. Aerodynamic optimization of civil aircraft design based on advanced computational fluid dynamics[D]. Beijing:Tsinghua University, 2010. (in Chinese) 张宇飞. 基于先进CFD方法的民用客机气动优化设计[D]. 博士学位论文. 北京: 清华大学, 2010. (  0) 0) |
| [86] |
Zhao T. Aerodynamic optimization design of supercritical wing based on structure weight/deformation performance[D]. Beijing:Tsinghua University, 2016. (in Chinese) 赵童. 考虑结构重量变形的超临界机翼气动优化设计[D]. 博士学位论文. 北京: 清华大学, 2016. (  0) 0) |
| [87] |
Giannakoglou K C. Design of optimal aerodynamic shapes using stochastic optimization methods and computational intelligence[J]. Progress in Aerospace Sciences, 2002, 38(1): 43-76. DOI:10.1016/S0376-0421(01)00019-7 (  0) 0) |
| [88] |
Asouti V G, Kyriacou S A, Giannakoglou K C. PCA-enhanced Metamodel-assisted Evolutionary Algorithms for Aerodynamic optimization[M]//Application of Surrogate-based Global Optimization to Aerodynamic Design. Springer International Publishing, 2016:47-57.
(  0) 0) |
| [89] |
HacioĝLu A. A novel usage of neural network in optimization and implementation to the internal flow systems[J]. Aircraft Engineering and Aerospace Technology, 2005, 77(5): 369-375. DOI:10.1108/00022660510617095 (  0) 0) |
| [90] |
Ni A X, Zhang Y F, Chen H X. An improvement to NSGA-Ⅱ algorithm and its application in optimization design of multi-element airfoil[J]. Acta Aerodynamica Sinica, 2014, 32(2): 252-257. (in Chinese) 倪昂修, 张宇飞, 陈海昕. NSGA-Ⅱ算法的改进及其在多段翼型缝道参数优化中的应用[J]. 空气动力学学报, 2014, 32(2): 252-257. DOI:10.7638/kqdlxxb-2013.0095 (  0) 0) |
| [91] |
Liu J L. Intelligent genetic algorithm and its application to aerodynamic optimization of airplanes[J]. AIAA Journal, 2005, 43(3): 530-538. DOI:10.2514/1.7070 (  0) 0) |
| [92] |
Oyama A, Obayashi S, Nakamura T. Real-coded adaptive range genetic algorithm applied to transonic wing optimization[J]. Applied Soft Computing, 2001, 1(3): 179-187. DOI:10.1016/S1568-4946(01)00017-5 (  0) 0) |
| [93] |
Trapani G, Kipouros T, Savill A M. The design of multi-element airfoils through multi-objective optimization techniques[J]. CMES-Computer Modeling in Engineering and Sciences, 2012, 88: 107-138. (  0) 0) |
| [94] |
Madavan N. On improving efficiency of differential evolution for aerodynamic shape optimization applications[C]//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. 2004:4622.
(  0) 0) |
| [95] |
Zingg D W, Nemec M, Pulliam T H. A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization[J]. European Journal of Computational Mechanics/Revue Européenne de Mécanique Numérique, 2008, 17(1-2): 103-126. (  0) 0) |
| [96] |
Sugimura K, Obayashi S, Jeong S. Multi-objective optimization and design rule mining for an aerodynamically efficient and stable centrifugal impeller with a vaned diffuser[J]. Engineering Optimization, 2010, 42(3): 271-293. DOI:10.1080/03052150903171084 (  0) 0) |
| [97] |
Oyama A, Liou M S, Obayashi S. Transonic axial-flow blade optimization:Evolutionary algorithms/three-dimensional Navier-Stokes solver[J]. Journal of Propulsion and Power, 2004, 20(4): 612-619. DOI:10.2514/1.2290 (  0) 0) |
| [98] |
Chiba K, Obayashi S, Nakahashi K, et al. High-fidelity multidisciplinary design optimization of aerostructural wing shape for regional jet[C]//23rd AIAA Applied Aerodynamics Conference. 2005:5080.
(  0) 0) |
| [99] |
Chiba K, Makino Y, Takatoya T. Evolutionary-based multidisciplinary design exploration for silent supersonic technology demonstrator wing[J]. Journal of Aircraft, 2008, 45(5): 1481-1494. DOI:10.2514/1.33272 (  0) 0) |
| [100] |
Chiba K, Makino Y, Takatoya T. Evolutionary-based multidisciplinary design exploration for silent supersonic technology demonstrator wing[J]. Journal of Aircraft, 2008, 45(5): 1481-1494. DOI:10.2514/1.33272 (  0) 0) |
| [101] |
Jung S K, Choi W, Martins-Filho L S, et al. An implementation of self-organizing maps for airfoil design exploration via multi-objective optimization technique[J]. Journal of Aerospace Technology and Management, 2016, 8(2): 193-202. DOI:10.5028/jatm.v8i2.585 (  0) 0) |
| [102] |
Yamazaki W, Matsushima K, Nakahashi K. Aerodynamic design optimization using the drag-decomposition method[J]. AIAA Journal, 2008, 46(5): 1096-1106. DOI:10.2514/1.30342 (  0) 0) |
| [103] |
Poloni C, Mosetti G. Aerodynamic shape optimisation by means of hybrid genetic algorithm[J]. Zeitschrift fur Angewandte Mathematik und Mechanik, 1996, 76: 247-250. DOI:10.1002/(ISSN)1521-4001 (  0) 0) |
| [104] |
Foster N F, Dulikravich G S. Three-dimensional aerodynamic shape optimization using genetic and gradient search algorithms[J]. Journal of Spacecraft and Rockets, 1997, 34(1): 36-42. DOI:10.2514/2.3189 (  0) 0) |
| [105] |
Tang Z. Multi-objective optimization strategies using adjoint method and game theory in aerodynamics[J]. Acta Mechanica Sinica, 2006, 22(4): 307-314. DOI:10.1007/s10409-006-0014-9 (  0) 0) |
| [106] |
Tang Z, Désidéri J A, Périaux J. Multicriterion aerodynamic shape design optimization and inverse problems using control theory and nash games[J]. Journal of Optimization Theory and Applications, 2007, 135(3): 599-622. DOI:10.1007/s10957-007-9255-4 (  0) 0) |
| [107] |
Haryanto I, Utomo T S, Sinaga N, et al. Optimization of maximum lift to drag ratio on airfoil design based on artificial neural network utilizing genetic algorithm[C]//Applied Mechanics and Materials. Trans Tech Publications, 2014, 493:123-128.
(  0) 0) |
| [108] |
Asouti V G, Kampolis I C, Giannakoglou K C. A grid-enabled asynchronous metamodel-assisted evolutionary algorithm for aerodynamic optimization[J]. Genetic Programming and Evolvable Machines, 2009, 10(4): 373. DOI:10.1007/s10710-009-9090-5 (  0) 0) |
| [109] |
Hu Z, Jakiela M, Pitt D M, et al. Reducing aerodynamic vibration with piezoelectric actuators:a genetic algorithm optimization[C]//Smart Structures and Materials. International Society for Optics and Photonics, 2004:276-287.
(  0) 0) |
| [110] |
Ong Y S, Nair P B, Keane A J. Evolutionary optimization of computationally expensive problems via surrogate modeling[J]. AIAA Journal, 2003, 41(4): 687-696. DOI:10.2514/2.1999 (  0) 0) |
| [111] |
Madavan N. Aerodynamic shape optimization using hybridized differential evolution[C]//21st AIAA Applied Aerodynamics Conference. 2003:3792.
(  0) 0) |
| [112] |
Kang Y S, Park T C, Yang S S, et al. Multi disciplinary design optimization and performance evaluation of a single-stage transonic axial compressor[C]//ASME Turbo Expo 2012:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, 2012:361-369.
(  0) 0) |
| [113] |
Jones D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21(4): 345-383. DOI:10.1023/A:1012771025575 (  0) 0) |
| [114] |
Zhou Z, Ong Y S, Nair P B, et al. Combining global and local surrogate models to accelerate evolutionary optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(1): 66-76. DOI:10.1109/TSMCC.2005.855506 (  0) 0) |
| [115] |
Pehlivanoglu Y V, Yagiz B. Aerodynamic design prediction using surrogate-based modeling in genetic algorithm architecture[J]. Aerospace Science and Technology, 2012, 23(1): 479-491. DOI:10.1016/j.ast.2011.10.006 (  0) 0) |
| [116] |
Karakasis M K, Koubogiannis D G, Giannakoglou K C. Hierarchical distributed metamodel-assisted evolutionary algorithms in shape optimization[J]. International Journal for Numerical Methods in Fluids, 2007, 53(3): 455-469. DOI:10.1002/(ISSN)1097-0363 (  0) 0) |
| [117] |
Whitney E J, Sefrioui M, et al. Advances in hierarchical, parallel evolutionary algorithms for aerodynamic shape optimisation[J]. JSME International Journal Series B, 2002, 45(1): 23-28. DOI:10.1299/jsmeb.45.23 (  0) 0) |
| [118] |
Joly M M, Verstraete T, Paniagua G. Integrated multifidelity, multidisciplinary evolutionary design optimization of counterrotating compressors[J]. Integrated Computer-Aided Engineering, 2014, 21(3): 249-261. (  0) 0) |
| [119] |
Chernukhin O, Zingg D W. Multimodality and global optimization in aerodynamic design[J]. AIAA Journal, 2013, 51(6): 1342-1354. DOI:10.2514/1.J051835 (  0) 0) |
| [120] |
Karakasis M K, Giotis A P, Giannakoglou K C. Inexact information aided, low-cost, distributed genetic algorithms for aerodynamic shape optimization[J]. International Journal for Numerical Methods in Fluids, 2003, 43(10-11): 1149-1166. DOI:10.1002/(ISSN)1097-0363 (  0) 0) |
| [121] |
Praveen C, Duvigneau R. Low cost PSO using metamodels and inexact pre-evaluation:Application to aerodynamic shape design[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(9): 1087-1096. (  0) 0) |
| [122] |
Sun H, Lee S. Response surface approach to aerodynamic optimization design of helicopter rotor blade[J]. International Journal for Numerical Methods in Engineering, 2005, 64(1): 125-142. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [123] |
Song W, Keane A J. Surrogate-based aerodynamic shape optimization of a civil aircraft engine nacelle[J]. AIAA Journal, 2007, 45(10): 2565-2574. DOI:10.2514/1.30015 (  0) 0) |
| [124] |
Alexandrov N M, Lewis R M, Gumbert C R, et al. Approximation and model management in aerodynamic optimization with variable-fidelity models[J]. Journal of Aircraft, 2001, 38(6): 1093-1101. DOI:10.2514/2.2877 (  0) 0) |
| [125] |
Kampolis I C, Giannakoglou K C. A multilevel approach to single-and multiobjective aerodynamic optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(33): 2963-2975. (  0) 0) |
| [126] |
Backhaus J, Aulich M, Frey C, et al. Gradient enhanced surrogate models based on adjoint CFD methods for the design of a counter rotating turbofan[C]//ASME Turbo Expo 2012:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, 2012:2319-2329.
(  0) 0) |
| [127] |
Giannakoglou K C, Giotis A P, Karakasis M K. Low-cost genetic optimization based on inexact pre-evaluations and the sensitivity analysis of design parameters[J]. Inverse Problems in Engineering, 2001, 9(4): 389-412. DOI:10.1080/174159701088027771 (  0) 0) |
| [128] |
Song L, Guo Z, Li J, et al. Research on metamodel-based global design optimization and data mining methods[J]. Journal of Engineering for Gas Turbines and Power, 2016, 138(9): 092604. DOI:10.1115/1.4032653 (  0) 0) |
| [129] |
Jeong S, Murayama M, Yamamoto K. Efficient optimization design method using kriging model[J]. Journal of Aircraft, 2005, 42(2): 413-420. DOI:10.2514/1.6386 (  0) 0) |
| [130] |
Namura N, Obayashi S, Jeong S. Surrogate-based multi-objective optimization and data mining of vortex generators on a transonic infinite-wing[C]//Evolutionary Computation (CEC), 2013 IEEE Congress on. IEEE, 2013:2910-2917.
(  0) 0) |
| [131] |
Dulikravich G S, Martin T J, Colaço M J, et al. Automatic switching algorithms in hybrid single-objective optimization[J]. FME Transactions, 2013, 41(3): 167-179. (  0) 0) |
| [132] |
Song L, Luo C, Li J, et al. Automated multi-objective and multidisciplinary design optimization of a transonic turbine stage[J]. Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2012, 226(2): 262-276. DOI:10.1177/0957650911425005 (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


