在航空航天领域,各学科数值模拟技术日臻成熟,基于高可信度数值模拟的优化设计方法在飞行器的设计中得到越来越广泛的应用。例如NASA发布的CFD愿景2030研究报告中[1],将多学科分析与优化列为需要重点发展的六大关键领域之一。在飞行器设计涉及的学科中,气动设计是非常基础和重要的一环,直接影响整个飞行器的飞行性能和飞行品质,对飞行安全、飞行效率与经济性等都具有决定性的影响。以大型运输机为例,全机1%的阻力增加会降低飞机7.6%的有效载荷[2];有资料显示,对于一架DC-10大小的飞机,升阻比每提高1%,每年可节约$100, 000美元的燃料费[3]。同时,飞行器气动设计结果作为机体结构与系统设计的基础,也是影响飞行器结构、飞行控制系统设计的关键。因此,可以说气动设计决定了飞行器的“灵魂”。伴随着各类飞行器及其设计技术的发展,人们在不断追寻着更好的气动设计方法,建立更有力的气动设计手段,以获得更优异的气动性能。
气动设计的基础涉及空气动力学反问题。鉴于空气动力学问题本身的复杂性与求解难度,20世纪60年代以前,在飞行器设计中,气动设计主要依赖大量的风洞实验结合设计人员的工程经验,通过所谓的“Cut-and-Try”的方式完成,这种方法需要投入大量的人力、物力和财力。随着计算机技术与数值计算方法的不断发展,CFD技术在飞行器气动分析和设计中扮演了越来越重要的角色,从速度势方程、Euler方程发展到Navier-Stokes方程的数值求解,计算网格从最初的几万到现在的几百万甚至几千万,数值模拟精度越来越高,可以进行三维机翼、翼身组合体、机翼/发动机/增升装置以及全机复杂绕流计算,为飞行器气动设计提供了可靠的分析手段,使得CFD在飞行器初步选型设计阶段可以大量取代风洞试验,提高了设计水平与效率,降低了研制成本。例如,美国Boeing公司在研制波音787客机中广泛采用了CFD数值模拟技术,从高速机翼设计,到发动机短舱设计,以及翼尖小翼设计,增升系统构型设计,机翼结冰的模拟,噪声的分析预测等[4]。
空气动力反问题的研究始于翼型设计,翼型反设计思想的提出可追溯到20世纪30年代NACA6系列翼型的设计[5],1945年Lighthill[6]提出了翼型反设计方法,该研究为翼型反设计方法的发展奠定了理论基础。由于反设计需要以掌握“优秀”的压力分布为基础,十分依赖设计者的经验,因此影响了其在飞行器气动外形设计中的应用。到20世纪80年代,随着CFD技术的快速发展与不断完善,将优化理论与CFD相结合,逐渐形成了气动外形设计新的方向。近年来,由于计算机技术的飞速发展,包括CFD、CSD等工程计算技术的日渐成熟,催生了多学科优化设计技术(MDO),并将进一步影响未来高性能飞行器的发展。然而,尽管气动优化设计经过几十年的发展取得了一系列重要成果,但是由于气动优化设计涉及到的学科方向众多,例如计算流体力学、几何造型学、网格生成技术、数据拟合、数值优化等等,各学科方向都有各自存在问题,使得相关的研究难度较大。另一方面,由于气动分析计算特别是对于复杂外形或涉及激波、分离等复杂流动问题时,CFD本身计算量巨大,计算精准度难以保证,也给气动优化设计研究造成了一些困难。因此,目前基于高可信度CFD的气动优化设计还主要集中在学院式的探讨,尚未在工程型号研制中得到大规模应用。为了给气动外形优化设计提供统一的研究和交流平台,欧美等国家已经开始为气动优化设计量身定制标准算例和研究课题:在美国方面,为了满足工业界对基于CFD的气动外形数值优化方法的强烈需求,美国航空航天学会AIAA组织的空气动力优化设计讨论组(Aerodynamic Design Optimization Discussion Group, ADODG)在2014年成立。类似于DPW阻力预测会议,ADODG相继发布了一系列标准气动优化问题,研究人员分别通过自己的方法对标准模型进行气动优化,来评估当前各种气动优化方法的能力。在欧洲方面,为了深入地研究评估基于代理模型全局优化方法在气动设计中的能力,GARTEUR Action Group (AD/AG52)[7]于2013年初成立。研究组计划通过联合欧洲研究人员,通过三年的时间开展对基于代理模型气动优化设计的系统研究,完成包括代理模型之间的对比,优化算法的比较,参数化与动网格方法等研究。近年来,更多的研究将针对解决实际工程设计中的复杂问题,开展包括处理代理模型所面临“维度灾难”、复杂多目标设计空间的减缩以及稳健性优化设计等一系列更具挑战性的问题。
国内空气动力研究人员开展了大量有关空气动力反设计方法和气动优化设计方法的研究,“十二五”以来,有关单位组织了联合研究,发展了相关的计算与设计程序,取得了良好的研究成果。但是,国内有关气动外形设计方法的专题研究和讨论相对较少,本文根据作者及课题组多年研究的积累,结合国内外相关的研究成果,主要从气动设计问题与涉及的研究方法等角度,对气动外形设计方法的发展及其面临的主要问题进行归纳与整理,并对未来气动外形设计的研究方向进行了展望,希望能为气动设计相关研究人员提供参考。
1 气动外形设计方法的发展 1.1 反设计方法反设计方法的核心是通过给定流场信息,如物面边界的压力分布,求得相应物体的几何外形。Lighthill[6]通过保角变换实现了二维翼型的反设计,并研究了翼型表面压力分布需要满足的约束条件,奠定了反设计方法的理论基础。70年代后,反设计方法的研究由不可压缩流动转向可压缩流动,研究的核心从方法的精度和效率转移到了实际工程应用[8]。Steger和Klineberg[9]提出了适合跨声速流动的小扰动反方法,Carlson[10]研究了一种笛卡尔网格上跨声速流动的反设计方法,Sobieczky[11]提出一种虚拟气体法,实现无激波翼型反设计。80年代初,Takanashi[12]由小扰动速势方程推导出翼型几何和压力分布的近似积分解,提出了余量修正法,Weed[13]和Henne[14]等将反设计方法拓展到三维机翼反设计,NASA的Campbell和Smith[15]发展了一种表面曲率法。我国张仲寅教授、华俊教授等根据余量修正法,开展了翼型、机翼反设计方法研究,在超临界翼型、机翼设计方面取得了大量的研究成果[16-18]。进入21世纪以来,随着数据挖掘技术的发展,Bui-Thanh等[19]基于POD和数据填补技术,发展了Gappy POD翼型反设计方法,邱亚松[20]提出改进的GappyPOD方法,李思怡[21]等在对GappyPOD反问题的误差分析基础上,提出了样本逐次逼近的差量Gappy POD方法(图 1),通过差量法去除常量相关误差,并通过逐次样本逼近策略减小非线性误差,形成了能够克服非线性影响的翼型反设计方法,提高了反设计精度及鲁棒性。

|
图 1 样本逐次逼近的差量Gappy POD翼型反设计方法[21] Figure 1 Successive sample-approximating Gappy POD airfoil inverse design approach |
反设计方法具有计算效率高,不需要大量CFD计算的优点,只要掌握目标翼型/机翼的表面压力分布,即可以获得所需要的翼型/机翼。然而在实际应用中,设计者难以获得正确的目标压力分布,为此,李焦赞[22]在反设计方法中引入压力分布优化,以扩展反设计方法的应用。尽管如此,对于满足新的不同设计要求的翼型或三维机翼设计而言,如何提出理想的目标压力分布仍然存在较大的难度,因此在很大程度上限制了反设计方法的进一步发展和应用。
1.2 优化设计方法与反设计方法相比,优化设计具有更大的灵活性和适应性。气动优化设计方法是把CFD技术与优化理论结合,将设计问题转化为满足一定几何和物理约束的求解目标函数的极值问题,利用现代计算机的高速计算能力,实现更加自动、鲁棒的气动设计,有效地提高气动特性。优化设计方法不但可以把压力分布差作为目标,处理传统的气动反设计问题,而且可以选取升力、阻力、力矩系数等与飞行器气动性能直接相关的要素作为目标函数,对目标特性进行优化设计。同时,在处理约束条件时,可以根据工程设计要求,构建相应的约束条件,结合适当的优化方法,将有约束问题转化为无约束问题。因此,优化设计方法更容易解决工程复杂问题。20世纪70年代,Hicks等[23]首次将数值优化的思想引入到翼型的设计中,此后气动外形优化设计(Aerodynamic Shape Optimization,ASO)得到越来越广泛的研究和应用。
气动优化设计首先需要建立必要的优化模型,包括根据设计要求提出优化的目标函数,即根据飞行器性能要求中涉及的空气动力特性,选择适当条件下的气动特性参数,如确定飞行速度、高度等条件下的升力、阻力或力矩系数等;提出描述几何外形变化空间的设计变量与适当的设计空间,同时结合相关的工程设计约束,建立相应的约束条件。开展气动优化设计,需要在提出优化设计模型基础上,建立包括参数化几何模型与动态网格生成、基于CFD或代理模型的气动特性计算以及数值优化方法等,其流程框架如图 2所示。
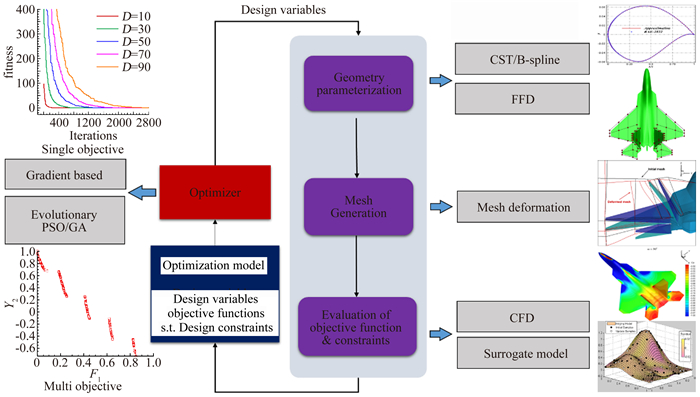
|
图 2 气动外形优化设计流程图 Figure 2 Flowchart of aerodynamic shape optimization |
基于梯度信息进行寻优是传统优化中应用最广泛的方法,梯度法利用目标函数对各设计变量的偏导数形成的梯度,寻找最有利的搜索方向,重复迭代直到收敛到一个局部极值。常用的基于梯度的优化方法有最速下降法,共轭梯度法,拟牛顿法,序列二次规划等。获得梯度信息最简单的方法是有限差分法,即单独扰动每个设计变量,用CFD分析程序计算扰动前后的目标函数值,以目标函数值增量与扰动增量的比值作为该设计变量的敏感性导数。Hicks和Henne[23-24]最早通过有限差分的方法求解目标函数的梯度信息,成功将梯度优化方法应用到翼型和机翼的设计中;Reuther等[25]应用此方法对超声速运输机机翼-机身的进行了气动优化设计。基于有限差分的优化方法简单直观,但是梯度计算量随着设计变量数目的增加而增大,因此该方法受到了很大的限制,只在简单的布局和设计变量较少的气动优化中得到应用。
伴随方法的提出使得梯度的计算量与设计变量数目无关,大大减小了梯度的计算时间。该方法以偏微分方程系统控制的数学理论为基础,把物体边界形状当作控制函数,流动主控方程作为等式约束,而设计目标则通过目标泛函来表达,将设计问题转变为一个寻求满足约束的最优控制问题,求梯度只需大约两倍流场计算的计算量。Jameson[26]首次将控制理论应用到气动设计中,此后以Jameson教授[27-28]、NASA Ames研究中心Reuther教授[29-30]、斯坦福大学Alonso教授[31-32]、麦吉尔大学Nadarajah教授[33-34]、多伦多大学Zingg教授[35-36]、密歇根大学Martins教授[37-39]这些人为代表的课题组在应用伴随方法进行气动优化设计方面进行了系统深入的研究,并取得了一系列的研究成果,先后运用速度势方程、Euler方程和Navier-Stokes方程对翼型、机翼、翼身组合体乃至全机进行了一系列的优化设计研究(图 3)。国内研究人员对伴随优化方法也开展了许多研究,西北工业大学的杨旭东[40]、熊俊涛[41]、左英桃[42]等,南京航空航天大学的唐智礼[43]、夏健[44]、刘学强[45]等,中国空气动力发展研究中心的邓有奇[46]、黄勇[47]、吴文华[48]等,都分别应用伴随方程法在基于梯度的气动外形优化设计方面开展了研究。
|
图 3 应用伴随方法进行大规模设计变量三维复杂气动外形优化设计[37-38] Figure 3 Application of adjoint method in 3D complex aerodynamic shape optimization with large-scale design variables |
大量的研究成果表明了伴随方法对于复杂外形气动优化设计问题的可行性,但不可否认的是,伴随方法只解决了梯度快速求解的问题,对于多极值气动优化问题,伴随方法有可能陷入局部最优解,无法保证得到全局最优解。另一方面,基于伴随的优化方法在处理多目标优化问题时会遇到困难,目标权系数的选取需要很强的经验,不恰当的权系数可能导致失败的设计结果。
1.2.2 基于进化计算的优化方法进化算法擅长处理非连续,多峰值,多约束和多目标优化问题,应用进化算法进行气动优化设计的出发点是认为气动设计是一个多极值优化问题。进化算法直接把CFD计算当成黑盒子调用,容易编程和实现并行计算、使用方便而且适用性强。作为进化算法中最具代表性的算法,遗传算法在气动优化设计中得到成功应用,Yamamoto[49]首次将遗传算法引入到气动外形设计中,Della等[50-51]利用遗传算法对翼型进行了优化设计,Oyama和Obayashi等[52-53]利用大型计算集群,基于三维可压缩NS方程,利用遗传算法对三维机翼完成了一系列气动优化设计,Holst等[54-55]提出了实数编码遗传算法,并对基于遗传算法的单目标和多目标优化设计做了系统的阐述,Yongsheng Lian[56]和Antunes[57]分别对进化算法在气动设计中的应用做了综述研究。20世纪90年代末,国内的王晓鹏[58]、隋洪涛[59]等率先对遗传算法在气动优化设计中的应用做了较为详细的研究。此后,为了提高优化搜索能力与优化效率,出现了遗传算法的改进算法、粒子群搜索算法、自适应差分进化等在气动优化设计中的应用研究[60-61],显示了进化算法在气动外形优化设计中的应用价值,体现了进化算法在全局优化方面的优势。
进化算法应用于气动优化设计最大问题是其收敛缓慢,需要大量调用原始高精度计算模型,当设计变量和设计目标数目增加时,利用进化算法进行高精度CFD的气动设计需要巨大的计算量甚至无法完成。由于优化效率低下,使得直接采用CFD计算和进化算法进行气动优化设计受到限制。
1.2.3 基于代理模型的全局优化方法代理模型(响应面模型,近似模型)是指在工程分析和设计中,可以替代非常耗时的原始物理模型的近似数学模型,也称为“模型的模型”。基于代理模型的全局优化方法既能利用代理模型的减少原始模型计算次数的优势,又能利用进化算法的全局寻优能力,因此在工程设计中倍受青睐[62-63]。代理模型在飞行器设计中的应用可以追溯到20世纪70年代,最初应用到结构优化设计[64]中,后来发展成为多学科优化设计的主要工具[65]。20世纪90年代末, 代理模型方法被引入到气动优化设计中[66],此后,基于代理模型的气动优化设计(图 4)发展成为并列于伴随方法的另一个热门的研究方向。
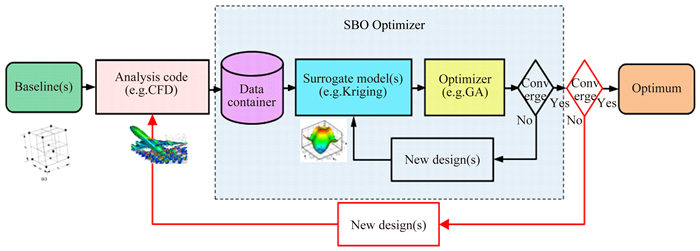
|
图 4 基于代理模型的气动优化设计框架[83] Figure 4 Framework of surrogate based aerodynamic shape optimization |
作为最具有代表性的代理模型,Kriging模型首次由Sacks等[67]引入到确定性计算机实验的设计和分析领域,Jones[68]等提出了基于代理模型高效的全局优化的思想,通过平衡局部挖掘和全局探索,不断加点更新代理模型,后来发展成为基于代理模型全局气动优化设计的主体框架。Jeong[69]将Kriging模型和遗传算法应用到翼型和襟翼位置的优化设计中,通过EI加点准则,保证了优化结果的全局最优;Song等[70]使用多目标遗传算法和Kriging模型对亚声速的发动机短舱进行了气动优化设计。对于气动优化设计中的代理模型,关键问题是如何利用更少的计算花费构造更高精度的代理模型。为此,一些新的代理模型构建方法也成功应用到气动设计中,包括梯度增强代理模型[71-72],变可信度代理模型[73-76],双层代理模型[77]等。近年来,出现了包括基于POD/PCA的代理模型[78-80]等研究。
Giannakoglou等[81]以及Forrester等[82]对使用近似模型和进化算法进行气动设计进行了综述研究,尽管代理模型大大降低了原始模型的计算次数,为全局优化提供了可能,但是对于设计变量规模较大或广义设计空间较大的问题,代理模型的精度将大幅下降,出现了代理模型的“维度灾难”问题。对于气动设计而言,特别是精细化气动外形设计中,代理模型的“维度灾难”问题将是影响其应用的关键问题。
1.2.4 基于梯度与进化类算法应用对比针对梯度优化和进化类算法的特点,文献[84-87]对比分析了其在气动优化设计中的各自优势与发展方向。基于伴随方程的梯度优化方法,设计变量规模的适应性强,可方便地应用于大规模设计变量问题。但是由于梯度优化方法本身局部优化特点,这类方法对于求解单峰问题或初值接近最佳值附近的优化设计问题具有明显的优势。Chernukhin[88]基于RANS方程,详细研究了气动外形设计空间的多峰性问题,文中认为气动设计空间的多峰性与设计变量的变化范围及外形变形程度有关,设计变量变化越宽,引起外形变化程度越大,气动设计空间越呈现出多峰性。三维机翼的优化和翼身融合布局设计是多峰性问题,推荐使用全局优化算法;一般的跨声速超临界翼型设计和机翼剖面形状的设计则多是单峰问题,梯度算法比较适合。因此,不同的气动优化设计问题有不同气动设计空间的特征,需要根据具体问题选择最合适的气动优化方法。
为了充分利用全局优化和梯度优化各自的优点,一些混合气动优化方法被提出[89-90],这些方法的基本思想是:首先采用少的设计变量进行全局气动优化,然后采用多设计变量进行梯度优化,既保证了全局性又提高了收敛性。
2 多目标与稳健性气动优化设计实际工程气动设计中,设计结果需要满足不同飞行条件、不同气动特性的设计要求,例如对于跨声速运输机机翼气动设计,不仅需要考虑巡航飞行条件下高升阻比以提高飞行效率,还要求其具有良好的低速高升力特性,同时设计机翼应具有良好的抖振边界;旋翼翼型设计,需要兼顾前飞、机动和悬停等不同飞行条件的飞行性能要求;战斗机机翼设计,需要兼顾亚、跨、超声速条件下机翼的升阻和力矩特性。另一方面,设计结果还要考虑加工制造及飞行高度、速度及迎角等不确定因素的影响,以保证稳健的气动性能。因此,工程中的气动外形设计通常涉及多目标多约束条件的稳健优化设计。
2.1 多点加权平均方法处理多目标问题最简单的方法是加权平均的方法,将多个设计目标通过权值向量聚合成一个目标,将多目标优化转换为单目标优化。加权方法是气动设计中最早使用的方法,Drela[91]给出了巡航构型下使用加权平均方法进行翼型多点气动设计的算例; Reuther等[92-93]详细论述了使用高精度CFD方法和伴随方法对复杂外形在几何约束条件下的多点设计问题;Szmelter[94]基于欧拉-边界层修正的伴随方法对三维机翼进行了多点设计;Susan[95]基于Euler方程的伴随方法,对美国NASA高速民用飞机项目模型进行了考虑机翼/机身/发动机短舱多个几何约束下的单点和多点的气动优化设计;Zingg教授[96]所带领的研究团队,针对多点气动设计问题展开了系列研究,提出了多点自适应加权方法[97]和积分方法[98],可以同时考虑18个设计点[99]。
加权平均的方法简单直观, 处理方便,各类改进的加权方式在基于伴随方法的多点优化中得到广泛应用。加权平均方法最大的问题是权系数的选择强烈地依赖设计者的经验和意愿,如果权系数给的不合理,将无法获得需要的设计结果,甚至导致设计重来,降低了设计效率。另一方面,加权平均的方法只能给出单一的设计结果,无法得到目标间的折衷关系,不利于设计者对问题本身进行深入分析。
2.2 多目标进化方法基于Pareto最优解集的进化多目标算法[100]可以通过一次运行得到最优解集,在气动设计中得到非常广泛的应用。Marco等[101]基于Euler方程,利用多目标遗传算法对翼型进行了气动优化设计;以色列的Epstein和Peigin利用自主开发的飞行器设计软件OPTIMAS,分别对二维翼型[102],单独机翼[103],翼身组合体[104],翼身融合飞翼布局飞机[105],通用商务喷气飞机[106]进行了多目标多约束的优化设计;意大利帕多瓦大学Ernesto教授的团队应用多目标进化算法分别对多段翼翼型[107]、旋翼翼型[108]、旋翼机的部件[109]进行了多目标设计; 日本东北大学Obayashi和Sasaki等研究人员,利用多目标进化算法针对超声速机翼开展了一系列的多目标优化设计[110-111];Leifsson[112]结合变可信度模型,空间映射和多目标进化算法,构建了基于代理模型的多目标气动优化框架,对跨声速翼型和低速翼型进行了多目标设计。国内的王荣伟[113]应用改进多目标粒子群算法对翼型进行了多目标优化设计,王超[114]应用多目标进化算法对战斗机小展弦比薄机翼进行了考虑跨声速和超声速多设计状态的气动优化设计,李权等[115]采用CFD技术和数值优化技术构建了基于工程环境的气动多目标优化设计平台,赵轲[116]开展了高维多目标气动优化方法的研究,应用目标降维与分层约束的方法对旋翼翼型进行了设计。
多目标进化方法的优势是可以通过一次运行获得Pareto最优解集,提供给设计者丰富的设计结果。设计者可以通过分析最优解集数据,有针对性地改进算法,获得目标之间的平衡关系。由于在优化搜索过程中,需要依赖大量的样本和多轮次的进化迭代,使得优化过程需要大量的CFD计算。尽管采用代理模型可以在一定程度上减少CFD的计算,当设计变量规模增大时,基于代理模型的多目标进化方法依然会面临“维度灾难”问题。另一方面,对于高维多目标问题,进化算法的收敛性也会急剧下降[117],给基于多目标进化算法的气动设计带来了新的问题。
2.3 稳健设计方法传统优化设计模型中,设计变量、目标函数和约束函数均为确定性的,即在某一个或几个确定的设计状态点上,通过优化算法搜索得到一个确定性的理想状态性能最优解。由于不能够反映加工制造过程以及飞行环境等客观存在的大量不确定性因素对设计结果的影响,使得传统优化设计的最优解对一些不确定性因素可能非常敏感而不能稳定的发挥其效能。稳健性设计方法可以克服传统确定性气动优化设计的结果对随机不确定性波动敏感性强的问题,通过控制设计目标的均值和方差来实现设计对象的性能和稳健性之间的平衡。日本的田口玄一博士[118]最先将稳健性的概念引入到产品设计中,确立了稳健设计的基本原理,Huyse和Padula等[119-122]将考虑不确定因素的稳健设计引入到气动设计中,国内王宇[123]构建了基于确定性Kriging的渐近全局方法,并以此为基础开展了飞机总体稳健性优化设计工作,白俊强等[124]进行了超临界翼型的稳健性优化设计, 黄江涛[125]用代理模型对超临界机翼进行了考虑机身干扰的稳健性优化设计,李焦赞[126]开展了几何不确定性的翼型多目标稳健优化设计,李静[127]同时考虑马赫数和升力系数等多个不确定因素影响,建立了自然层流翼型稳健设计方法。在稳健设计中,如何构建不确定性影响模型是影响设计结果及其效率的关键,为此,赵轲[128-129]研究了混沌多项式展开不确定分析方法,并对层流超临界翼型进行了稳健性设计。
稳健设计可以充分考虑不确定因素的影响,但是不确定分析需要大量的气动数据,造成其在实际工程的气动设计中难以得到充分体现。在工程气动设计中一般通过多点设计的简化模型完成,由于缺乏对不确定性因素的完整模拟,如何选点以及如何加权等都受到一定的经验的制约。因此,怎样将稳健性设计理论与实际工程经验相结合,平衡计算花费与不确定分析的精度是工程气动设计需要研究的问题。
3 研究展望 3.1 气动设计空间的特性研究气动设计空间的特征与设计状态、目标函数、约束条件有很大的关系,气动设计空间的多峰性问题直接影响优化方法和搜索空间的选择。一般说来,对于单极值的气动设计问题或者具有良好初始外形气动设计问题来说,可选用局部优化搜索能力强的方法,基于伴随的梯度优化便是最佳选择;对于多极值的气动设计问题,必须采用全局优化算法才能保证设计结果的可靠性。然而对于一个全新的气动设计问题而言,通常缺乏先验的知识,采用具有全局搜索能力的优化方法以及选择更大的设计空间,将可能得到更好的设计结果或为设计人员提供更多的参考。
3.2 高维设计空间的全局优化由于对气动设计空间特征的未知,更可靠的设计便是采用全局优化方法。伴随方法解决了大规模设计变量的问题,但是无法实现全局优化,基于代理模型的优化可以实现设计空间的全局探索,但是在高维设计空间,代理模型和优化算法将面临“维度灾难”。构建代理模型需要的样本规模以及优化过程中的需要的搜索规模会随着设计变量的增加呈指数型增长,样本的稀疏性造成代理模型精度急剧下降,设计空间的暴增会造成优化算法无法收敛。因此高维设计空间的全局优化设计仍然是气动外形设计最大的难题,也是当前的研究热点之一。为了解决这一难题,可以采用一些混合方法,例如梯度算法和进化算法相结合可以改善优化的全局性和收敛性,梯度增强代理模型、变可信度代理模型、分层代理模型、混合代理模型等可以提高全局代理模型的精度等等。另一方面,可以采用自适应搜索空间的方法[130]实现全局优化,通过自适应增加设计变量数目,可以有效减小不必要的搜索空间,大大提高寻优效率。
3.3 高维目标空间的优化与可视化对于高维目标空间的优化问题,采用基于Pareto概念的多目标进化算法可以获得分布性良好的最优解集,但是当目标大于3个以后,多目标进化算法的收敛性急剧下降。采用多目标加权的方法可以很好的解决最优解集的收敛性问题,但牺牲的是解的多样性。为了缓解这一矛盾,可以采用分解优化的思想,将多目标优化转换为一系列单目标优化问题。但是要想获得分布性良好的最优解集,分解的数目仍然会随着目标维数的增加而呈指数级增加,由此引发高维目标的“维度灾难”。因此,如何在高维目标空间寻求收敛性和多样性最合适的折衷和平衡是一项重要的研究内容。另一方面对于高维多目标优化问题,最终得到的优化解集是抽象的高维超曲面,优化结果的可视化成为难点,导致设计者难以对设计结果进行决策,因此高维目标空间的可视化也是研究的重点。
3.4 气动数据库与智能设计国内外研究人员通过各种方式积累了大量的气动数据,但是由于种种原因,这些气动数据没有被系统的整理和归纳,造成了数据的搁置和浪费。以翼型数据为例,已公开的传统的翼型数据库只能满足旧式飞机的设计,已不能满足现代高性能飞行器的设计要求,而学术论文中报告的先进翼型及气动数据没有公开,造成工程型号研制单位依然难以借鉴和使用。
在智能设计方面,虽然进化计算和群体智能的优化方法已经广泛应用于气动设计,但是智能气动设计还远没有实现,当前的气动设计依然需要很强的人工经验和干预,气动设计成本依然很高。通过机器学习和数据挖掘手段可以发现气动数据中的知识和规律,例如数据降维和可视化等[131-132]已经在气动设计中得到应用。近年来,Poole等[133]根据翼型的几何数据和气动性能确定了翼型的评价指标体系,建立了包含977个翼型的数据库,实现了数据驱动的翼型设计。这种基于翼型大数据的智能设计思想具有非常深远的意义,更广泛和更深层次的智能设计方法在气动设计中的应用有待探索和挖掘。
基于数据的智能时代已经来临,在新的科技革命的大趋势下,气动设计学科也要融合先进的理念和技术,通过构建丰富的气动数据库,结合人工智能技术,实现多学科融合环境下的气动设计,完成气动设计理念新的革命。
4 总结气动外形设计方法是实现飞行器气动布局与气动部件精细化设计的重要手段,对提高飞行器的气动性能与设计效率具有重要意义。本文回顾了气动外形设计方法的发展历程,重点讨论了气动外形反设计方法、优化设计方法以及多目标和稳健性优化方法,对飞行器复杂气动外形设计所面临的新问题和新挑战进行了总结,最后提出了对未来气动外形设计的研究展望。气动外形设计的研究不是一蹴而就的,需要建立在对计算空气动力学和优化设计方法有全局的把握和认识的基础上,逐步推进,从而完成整个气动设计技术的迭代和升级。
| [1] |
Slotnick J, Khodadoust A, Alonso J, et al. CFD Vision 2030 study:a path to revolutionary computational aerosciences, NASA/CR-2014-218178[R]. Hampton:NASA Langley Research Center, 2014.
(  0) 0) |
| [2] |
Jameson A, Martinelli L, Vassberg J. Using computational fluid dynamics for aerodynamics-a critical assessment[R]. ICAS paper 2002-1.10.1, Toronto.
(  0) 0) |
| [3] |
Lynch F T. Commercial transports-aerodynamic design for cruise performance and efficiency[R]. Dauglas Aircraft Company, 1981:7026.
(  0) 0) |
| [4] |
Jameson A. Computational fluid dynamics and airplanedesign:its current and future im-pact[R]. Lecture in University of Cincinnati, Feb. 22, 2008
(  0) 0) |
| [5] |
Jacobs E N, Ward K E, Pinkerton R M. The characteristics of 78 related airfoil sections from tests in the variable-density wind tunnel[R]. NACA Rept. 460, 1933.
(  0) 0) |
| [6] |
Lighthill M J. A new method of two-dimensional aerodynamic design[R]. R & M 2112, Aeronautical Research Council, London, 1945.
(  0) 0) |
| [7] |
GARTEUR AD/AG52 Members (2013) Partial report on surrogate-based global optimization methods in aerodynamic design[R]. 2013-2015.
(  0) 0) |
| [8] |
Strand T. Exact method of designing airfoils with given velocity distributions in incompressible flow[J]. Journal of Aircraft, 1973, 10(11): 651-659. DOI:10.2514/3.60278 (  0) 0) |
| [9] |
Steger J L, Klineberg J M. A finite-difference method for transonic airfoil design[J]. AIAA Journal, 1973, 11(5): 628-635. DOI:10.2514/3.50502 (  0) 0) |
| [10] |
Carlson L A. Transonic airfoil analysis and design using cartesian coordinates[J]. Journal of Aircraft, 1976, 13(5): 349-357. DOI:10.2514/3.58667 (  0) 0) |
| [11] |
Sobieczky M, Yu N J, Fung K Y, et al. New method for designing shock-free transonic configurations[J]. AIAA Journal, 1979, 17(7): 722-729. DOI:10.2514/3.61209 (  0) 0) |
| [12] |
Takanashi S. Iterative three-dimensional transonic wing design using integral equations[J]. Journal of Aircraft, 1985, 22(8): 655-660. DOI:10.2514/3.45182 (  0) 0) |
| [13] |
Weed R A, Carlson L A. Combined direct/inverse three dimensional transonic wing design with viscous and wing/body effects[R]. AD-A165466, 1984.
(  0) 0) |
| [14] |
Henne P A. Inverse transonic wing design method[J]. Journal of Aircraft, 1981, 18: 121-127. DOI:10.2514/3.57472 (  0) 0) |
| [15] |
Campbell R L, Smith L A. A hybrid algorithm for transonic airfoil and wing design[R]. AIAA-87-2552-CP, 1987.
(  0) 0) |
| [16] |
Hua Jun, Zhang Zhongyin, Qiao Zhide, et al. A transonic airfoil design method and examples[J]. Acta Aerodynamica Sinica, 1990, 8(2):117-123. (in Chinese) 华俊, 张仲寅. 一种跨声速翼型设计方法及设计诸例[J]. 空气动力学学报, 1990, 8(2): 117-123. (  0) 0) |
| [17] |
Bai Junqiang, Hua Jun, Zhang Zhongyin. Transonic airfoil design using euler equations[J]. Acta Aerodynamica Sinica, 1997, 15(4): 458-461. (in Chinese) 白俊强, 华俊, 张仲寅. 基于欧拉方程的跨声速翼型设计[J]. 空气动力学学报, 1997, 15(4): 458-461. (  0) 0) |
| [18] |
Zhan Hao, Hua Jun, Zhang Zhongyin. Design of multi-lifting surfaces based on iterative residual correction[J]. Acta Aeronautica Et Astronautica Sinica, 2003, 24(5): 411-413. (in Chinese) 詹浩, 华俊, 张仲寅. 基于余量修正原理的多翼面气动力反设计方法[J]. 航空学报, 2003, 24(5): 411-413. (  0) 0) |
| [19] |
Bui-Thanh T, Damodaran M, Willcox K. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J]. AIAA Journal, 2004, 42(8): 1501-1516. (  0) 0) |
| [20] |
Bai Junqiang, Qiu Yasong, Hua Jun. Improved airfoil inverse design method based on gappy POD[J]. Acta Aeronautica ET Astronautica Sinica, 2013, 34(4): 762-771. (in Chinese) 白俊强, 邱亚松, 华俊. 改进型GappyPOD翼型反设计方法[J]. 航空学报, 2013, 34(4): 762-771. (  0) 0) |
| [21] |
Li Siyi, Gao Zhenghong, Gao Chong, et al. A successive gappy proper orthogonal decomposition approach and its application to inverse airfoil design[R]. AIAA 2017-0709.
(  0) 0) |
| [22] |
Li Jiaozan, Gao Zhenghong, Zhan Hao. Study on inverse design method of airfoil based on optimization of target pressure distribution[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(1): 187-190. (in Chinese) 李焦赞, 高正红, 詹浩. 基于目标压力分布优化的翼型反设计方法研究[J]. 弹箭与制导学报, 2008, 28(1): 187-190. (  0) 0) |
| [23] |
Hicks R M, Murman E M, Vanderplaats G N. An assessment of airfoil design by numerical optimization[R]. NASA TM X-3092, 1974.
(  0) 0) |
| [24] |
Hicks R M, Henne P A. Wing design by numerical optimization[R]. AIAA-79-0080, 1979.
(  0) 0) |
| [25] |
Reuther J, Cliff S, Hichs R, et al. Practical design optimization of wing/body configurations using the euler equations[R]. AIAA-92-2633, 1992.
(  0) 0) |
| [26] |
Jameson A. Aerodynamic design via control theory[J]. Journal of Scientific Computing, 1988, 3: 233-260. DOI:10.1007/BF01061285 (  0) 0) |
| [27] |
Jameson A, Reuther J. Control theory based airfoil design using the Euler equations[R]. AIAA-94-4272, 1994.
(  0) 0) |
| [28] |
Jameson A, Pierce N A, Martinelli L. Optimum aerodynamic design using the navier-stokes equations[R]. AIAA-97-0101, 1997.
(  0) 0) |
| [29] |
Reuther J, Jameson A. Aerodynamic shape optimization of wing and wing-body configurations using control theory[R]. AIAA-95-0123, 1995.
(  0) 0) |
| [30] |
Reuther J, Jameson A, Farmer J, et al. Aerodynamic shape optimisation of complex aircraft configurations via an adjoint formulation[R]. AIAA-96-0094, 1996.
(  0) 0) |
| [31] |
Mader C, Martins J, Alonso J J, et al. ADjoint:an approach for the rapid development of discrete adjoint solvers[J]. AIAA Journal, 2008, 46(4): 863-873. DOI:10.2514/1.29123 (  0) 0) |
| [32] |
Marta A C, Mader C A, Martins J R R A, et al. A methodology for the development of discrete adjoint solvers using automatic differentiation tools[J]. International Journal of Computational Fluid Dynamics, 2007, 21(9): 307-327. (  0) 0) |
| [33] |
Nadarajah S K. The discrete adjoint approach to aerodynamic shape optimization[D]. Ph.D. Dissertation, University of Stanford, Stanford, CA, 2003. http://adsabs.harvard.edu/abs/2003PhDT........10N
(  0) 0) |
| [34] |
Nadarajah S K, Jameson A. Optimum shape design for unsteady flows with time-accurate continuous and discrete adjoint methods[J]. AIAA Journal, 2007, 45(7): 1478-1500. DOI:10.2514/1.24332 (  0) 0) |
| [35] |
Nemec M, Zingg D W. Newton-Krylov algorithm for aerodynamic design using the Navier-Stokes equations[J]. AIAA Journal, 2002, 40(6): 1146-1154. DOI:10.2514/2.1764 (  0) 0) |
| [36] |
David Koo, David W Zingg. Progress in aerodynamic shape optimization based on the reynolds-averaged Navier-Stokes equations[R]. AIAA 2016-1292.
(  0) 0) |
| [37] |
Lyu Z, Kenway G K, Martins J R R A. Aerodynamic shape optimization studies on the common research model wing benchmark[J]. AIAA Journal, 2015, 53(4): 968-985. DOI:10.2514/1.J053318 (  0) 0) |
| [38] |
Lyu Z, Martins J R R A. Aerodynamic design optimization studies of a blended-wing-body aircraft[J]. Journal of Aircraft, 2014, 51(5): 1604-1617. DOI:10.2514/1.C032491 (  0) 0) |
| [39] |
Song Chen, Zhoujie Lyu, Gaetan K W.Kenway, et al. Martins, aerodynamic shape optimization of common research model wing-body-tail configuration[J]. Journal of Aircraft, 2016, 53(1): 276-293. DOI:10.2514/1.C033328 (  0) 0) |
| [40] |
Yang Xudong. Aerodynamic design optimization based on control theory[D]. Northwestern Polytechnical University, 2002. (in Chinese) 杨旭东. 基于控制理论的气动优化设计技术研究[D]. 西北工业大学, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10699-2003101473.htm (  0) 0) |
| [41] |
Xiong Juntao, Qiao Zhide, Yang Xudong, et al. Optimum aerodynamic design of transonic wing based on viscous adjoint method[J]. Acta Aeronautica Et Astronautica Sinica, 2007, 28(2): 281-285. (in Chinese) 熊俊涛, 乔志德, 杨旭东, 等. 基于黏性伴随方法的跨声速机翼气动优化设计[J]. 航空学报, 2007, 28(2): 281-285. (  0) 0) |
| [42] |
Zuo Yingtao, Gao Zhenghong, Zhan Hao. Aerodynamic design method based on N-S equations and discrete adjoint approach[J]. Acta Aerodynamica Sinica, 2009, 27(1): 67-72. (in Chinese) 左英桃, 高正红, 詹浩. 基于N-S方程和离散共轭方法的气动设计方法研究[J]. 空气动力学学报, 2009, 27(1): 67-72. (  0) 0) |
| [43] |
Tang Zhili, Huang Mingke. Control theory based airfoil design using Euler equations[J]. Acta Aerodynamica Sinica, 2001, 19(3): 262-270. (in Chinese) 唐智礼, 黄明恪. 基于控制理论的Euler方程翼型减阻优化设计[J]. 空气动力学学报, 2001, 19(3): 262-270. (  0) 0) |
| [44] |
Xu Zhaoke, Xia Jian, Gao Yisheng. Continuous adjoint approach to aerodynamic optimization on 3D unstructured grids[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(1): 145-152. (in Chinese) 徐兆可, 夏健, 高宜胜. 基于三维非结构网格的连续伴随优化方法[J]. 南京航空航天大学学报, 2015, 47(1): 145-152. (  0) 0) |
| [45] |
Yang Yang, Ouyang Shaoxiu, Liu Xueqiang, et al. Aerodynamic optimization of transonic wing using discrete adjoint operator[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(3): 347-352. (in Chinese) 杨洋, 欧阳绍修, 刘学强, 等. 基于伴随算子的跨声速机翼气动优化设计[J]. 南京航空航天大学学报, 2013, 45(3): 347-352. (  0) 0) |
| [46] |
Li Bin, Deng youqi, Tang Jing, et al. Discrete adjoint optimization method for 3D unstructured grid[J]. Acta Aeronautica ET Astronautica Sinica, 2014, 35(3): 674-686. (in Chinese) 李彬, 邓有奇, 唐静, 等. 基于三维非结构混合网格的离散伴随优化方法[J]. 航空学报, 2014, 35(3): 674-686. (  0) 0) |
| [47] |
Huang Yong, Chen Zuobin, Liu Gang. An investigation of aerodynamic optimization design for airfoil based on adjoint formulation[J]. Acta Aerodynamica Sinica, 1999, 17(4): 413-422. (in Chinese) 黄勇, 陈作斌, 刘刚. 基于伴随方程的翼型数值优化设计方法研究[J]. 空气动力学学报, 1999, 17(4): 413-422. (  0) 0) |
| [48] |
Wu Wenhua, Fan Zhaolin, Chen Dehua, et al. Adjoint based on high precise aerodynamic shape optimization for transonic civil aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(6): 719-724. (in Chinese) 吴文华, 范召林, 陈德华, 等. 基于伴随算子的大飞机气动布局精细优化设计[J]. 空气动力学学报, 2012, 30(6): 719-724. (  0) 0) |
| [49] |
Yamamoto K, Inoue O. Application of genetic algorithm to aerodynamic shape optimization[R]. AIAA-95-1650, 1995.
(  0) 0) |
| [50] |
Quagliarella D, Della Cioppa A. Genetic algorithms applied to the aerodynamic design of transonic airfoils[J]. Journal of Aircraft, 1995, 32(4): 889. DOI:10.2514/3.46810 (  0) 0) |
| [51] |
De Falco I, DellaCioppa A, Iazzetta A, et al. Evolutionary algorithms for aerofoil design[J]. International Journal of Computational Fluid Dynamics, 1998, 11: 51-77. DOI:10.1080/10618569808940865 (  0) 0) |
| [52] |
Oyama A. Wing design using evolutionary algorithms[D]. PhD Thesis, Dept. of Aeronautics and Space Engineering, Tohcku University, Senadi, Japan, March 2000.
(  0) 0) |
| [53] |
Oyama A, Obayashi S, Nakamura T. Real-coded adaptive range genetic algorithm applied to transonic wing optimization[J]. Applied Soft Computing, 2001(1): 179-187. (  0) 0) |
| [54] |
Hoist T L, Pulliam T H. Evaluation of genetic algorithm concepts using model problems, part Ⅰ:single-objective optimization[R]. NASA TM in preparation, 2003.
(  0) 0) |
| [55] |
Hoist T L, Pulliam T H. Evaluation of Genetic Algorithm Concepts Using Model Problems, Part Ⅱ:mufti-objective optimization[R]. NASA TM 2003-212813, 2003.
(  0) 0) |
| [56] |
Akira Oyama, Meng-Sing Liou. Progress in design optimization using evolutionary algorithms for aerodynamic problems[J]. Progress in Aerospace Sciences, 2010, 46: 199-223. DOI:10.1016/j.paerosci.2009.08.003 (  0) 0) |
| [57] |
Antunes A P, Azevedo J L F. Studies in aerodynamic optimization based on genetic algorithms[J]. Journal of Aircraft, 2014, 51(3): 1002-1012. DOI:10.2514/1.C032095 (  0) 0) |
| [58] |
Wang Xiaopeng. Genetic algorithm and application in aerodynamic design optimization[D]. Northwestern Polytechnical University, 2000.(in Chinese) 王晓鹏. 遗传算法及其在气动优化设计中的应用研究[D]. 西北工业大学, 2000. http://cdmd.cnki.com.cn/Article/CDMD-10699-2000003204.htm (  0) 0) |
| [59] |
Sui Hongtao. Genetic algorithm and their application to aerodynamic optimization problems[D]. Nanjing University of Aeronautics & Astronautics, 2001. (in Chinese) 隋洪涛. 基因遗传算法及气动外形最优化设计[D]. 南京航空航天大学, 2001. http://cdmd.cnki.com.cn/article/cdmd-10287-2003051953.htm (  0) 0) |
| [60] |
Chang Yanxin, Gao Zhenghong. Application of adaptive differential evolutionary algorithms to aerodynamic optimization design[J]. Acta Aeronautica Et Astronautica Sinica, 2009, 30(9): 1590-1596. (in Chinese) 常彦鑫, 高正红. 自适应差分进化算法在气动优化设计中的应用[J]. 航空学报, 2009, 30(9): 1590-1596. (  0) 0) |
| [61] |
Li Ding, Xia Lu. Application of improved particle swarm optimization algorithm to aerodynamic design[J]. Acta Aeronautica ET Astronautica Sinica, 2012, 33(10): 1809-1816. (in Chinese) 李丁, 夏露. 改进的粒子群优化算法在气动设计中的应用[J]. 航空学报, 2012, 33(10): 1809-1816. (  0) 0) |
| [62] |
Lim D, Jin Y, Ong Y S, et al. Generalizing surrogate assisted evolutionary computation[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(3): 329-355. DOI:10.1109/TEVC.2009.2027359 (  0) 0) |
| [63] |
Giannakoglou K C. Design of optimal aerodynamic shapes using stochastic optimization methods and computational intelligence[J]. Progress in Aerospace Sciences, 2002, 38: 43-76. DOI:10.1016/S0376-0421(01)00019-7 (  0) 0) |
| [64] |
Schmit L A, Farshi B. Some approximation concepts for structural synthesis[J]. AIAA Journal, 1974, 12(5): 692-699. DOI:10.2514/3.49321 (  0) 0) |
| [65] |
Simpson T W, Mauery T M, Korte J J, et al. Kriging metamodels for global approximation in simulation-based multidisciplinary design optimization[J]. AIAA Journal, 2001, 39(12): 2233-2241. DOI:10.2514/2.1234 (  0) 0) |
| [66] |
Sevant N E, Bloor M I G, Wilson M J. Aerodynamic design of a flying wing using response surface methodology[J]. Journal of Aircraft, 2000, 37(4): 562-569. DOI:10.2514/2.2665 (  0) 0) |
| [67] |
Sacks J, Welch W J, Mitchell T J, et al. Design and analysis of computer experiments[J]. Tatistical Science, 1989, 4(4): 409-423. (  0) 0) |
| [68] |
Jones D R, Schonlau M, Welch W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492. DOI:10.1023/A:1008306431147 (  0) 0) |
| [69] |
Jeong S, Murayama M, Yamamoto K. Efficient optimization design method using kriging model[J]. Journal of Aircraft, 2005, 42(2): 413-420. DOI:10.2514/1.6386 (  0) 0) |
| [70] |
Song W, Keane A J. Surrogate-based aerodynamic shape optimization of a civil aircraft engine nacelle[J]. AIAA Journal, 2007, 45(10): 2565-2574. DOI:10.2514/1.30015 (  0) 0) |
| [71] |
Hyoung-Seog Chung, Juan J Alonso. Using gradients to construct response surface models for high-dimensional design optimization problems[R]. AIAA 2001-0922.
(  0) 0) |
| [72] |
Laurenceau J, Sagaut P. Building efficient response surfaces of aerodynamic functions with kriging and cokriging[J]. AIAA Journal, 2008, 46(2): 498-507. DOI:10.2514/1.32308 (  0) 0) |
| [73] |
Forrester A I J, Sóbester A, Keane A J. Multi-fidelity optimization via surrogate modelling[C]//Proceedings of the Royal Society A, 2008, 463:3251-3269. http://www.jstor.org/stable/20209374
(  0) 0) |
| [74] |
Han Z H, Zimmermann R, Goertz S. An alternative cokriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(5): 1205-1210. DOI:10.2514/1.J051243 (  0) 0) |
| [75] |
Huang Likeng, Gao Zhenghong. Research on multi-fidelity aerodynamic optimization methods[J]. Chinese Journal of Aeronautics, 2013, 26(2): 279-286. DOI:10.1016/j.cja.2013.02.004 (  0) 0) |
| [76] |
Koziel S, Leifsson L. Surrogate-based aerodynamic shape optimization by variable-resolution models[J]. AIAA Journal, 2013, 51(1): 94-106. DOI:10.2514/1.J051583 (  0) 0) |
| [77] |
Zhang Dehu, Gao Zhenghong, Huang Likeng, et al. Double-stage metamodel and its application in aerodynamic design optimization[J]. Chinese Journal of Aeronautics, 2011, 24(5): 568-576. DOI:10.1016/S1000-9361(11)60066-6 (  0) 0) |
| [78] |
Bracconnier T, et al. Toward an adaptive POD/SVD surrogate model for aeronautic design[J]. Comput. Fluids,, 2011, 40: 195-209. DOI:10.1016/j.compfluid.2010.09.002 (  0) 0) |
| [79] |
Iuliano E, Quagliarella D. Aerodynamic shape optimization via non-intrusive pod-based surrogate modelling[J]. Comput Fluids, 2013, 84: 327-350. DOI:10.1016/j.compfluid.2013.06.007 (  0) 0) |
| [80] |
Varvara G Asouti, Stylianos A Kyriacou, Kyriakos C Giannakoglou. PCA-enhanced metamodel-assisted evolutionary algorithms for aerodynamic optimization, application of surrogate-based global optimization to aerodynamic design[M]. Springer Tracts in Mechanical Engineering. https://link.springer.com/chapter/10.1007/978-3-319-21506-8_3?no-access=true
(  0) 0) |
| [81] |
Giannakoglou K C. Design of optimal aerodynamic shapes using stochastic optimization methods and computational intelligence[J]. Progress in Aerospace Sciences, 2002, 38(1): 43-76. DOI:10.1016/S0376-0421(01)00019-7 (  0) 0) |
| [82] |
Forrester A I J, Keane A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1): 50-79. (  0) 0) |
| [83] |
Han Zhonghua. Kriging surrogate model and its application to design optimization:A review of recent progress[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. (  0) 0) |
| [84] |
Obayashi S, Nakamura T. Comparison of optimization algorithms for aerodynamic shape design[R]. AIAA-96-2349, 1996.
(  0) 0) |
| [85] |
Widhalm M, Ronzheimer A, Hepperle M. Comparison between gradient-free and adjoint based aerodynamic optimization of a flying wing transport aircraft in preliminary design[R]. AIAA 2007-4060.
(  0) 0) |
| [86] |
Poole D J, Allen C B, Rendall T C S. Comparison of local and global constrained aerodynamic shape optimization[R]. AIAA 2014-3223.
(  0) 0) |
| [87] |
Zingg D W, Nemec M, Pulliam T H. A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization[R]. Shape Design in Aerodynamics, 2008, 17(1-2):103-126.
(  0) 0) |
| [88] |
Oleg Chernukhin, David W Zingg. Multimodality and global optimization in aerodynamic design[J]. AIAA Journal, 2013, 51(6): 1342-1354. DOI:10.2514/1.J051835 (  0) 0) |
| [89] |
Temesgen Mengistu, Wahid Ghaly. Global-and local-shape aerodynamic optimization of turbine blades[R]. AIAA 2006-6933.
(  0) 0) |
| [90] |
Jin Woo Yim, Byung Joon Lee, Chongam Kim. Multi-stage aerodynamic design of multi-body geometries via global and local optimization methods[R]. AIAA 2008-134.
(  0) 0) |
| [91] |
Drela M. Pros & cons of airfoil optimization[A]. Frontiers of Computational Fluid Dynamics 1998[M], edited by D. A. Caughey and M. M. Hafez, World Scientific, Singapore, 1998:363-381.
(  0) 0) |
| [92] |
Reuther J J, Jameson A, Alonso J J, et al. Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers, Part 1[J]. Journal of Aircraft, 1999, 36(1): 51-60. DOI:10.2514/2.2413 (  0) 0) |
| [93] |
Reuther J J, Jameson A, Alonso J J, et al. Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers, Part 2[J]. Journal of Aircraft, 1999, 36(1): 61-74. DOI:10.2514/2.2414 (  0) 0) |
| [94] |
Szmelter J. Multipoint aerodynamic wing optimization in viscous flow[J]. Journal of Aircraft, 2001, 38(5): 860-867. DOI:10.2514/2.2845 (  0) 0) |
| [95] |
Susan E Cliff, James J Reuther, David A Saunders, et al. Single-point and multipoint aerodynamic shape optimization of high-speed civil transport[J]. Journal of Aircraft, 2001, 38(6): 997-1005. DOI:10.2514/2.2886 (  0) 0) |
| [96] |
Marian Nemec, David W Zingg, Thomas H Pulliam. Multipoint and multi-objective aerodynamic shape optimization[J]. AIAA Journal, 2012, 42(6): 1057-1065. (  0) 0) |
| [97] |
Zingg D W, Elias S. Aerodynamic optimization under a range of operating conditions[J]. AIAA Journal, 2006, 44(11): 2787-2792. DOI:10.2514/1.23658 (  0) 0) |
| [98] |
Howard P Buckley, David W Zingg. Approach to aerodynamic design through numerical optimization[J]. AIAA Journal, 2013, 51(8): 1972-1981. DOI:10.2514/1.J052268 (  0) 0) |
| [99] |
Buckley H, Zhou B, Zingg D W. Airfoil optimization using practical aerodynamic design requirements[J]. Journal of Aircraft, 2010, 47(5): 1707-1719. DOI:10.2514/1.C000256 (  0) 0) |
| [100] |
Deb K. Multi-objective optimization using evolutionary algorithms[M]. New York: Wiley, 2001.
(  0) 0) |
| [101] |
Marco N, Désidéri J A, Lanteri S. Multi-objective optimization in CFD by genetic algorithms[R]. Institut National de Recherche en Informatique et en Automatique, Rept. 3686, 1999.
(  0) 0) |
| [102] |
Epstein B, Peigin S. Robust hybrid approach to multiobjective constrained optimization in aerodynamics[J]. AIAA Journal, 2004, 42(8): 1572-1581. DOI:10.2514/1.992 (  0) 0) |
| [103] |
Epstein B, Peigin S. Constrained aerodynamic optimization of three-dimensional wings driven by Navier-Stokes computations[J]. AIAA Journal, 2005, 43(9): 1946-1957. DOI:10.2514/1.10308 (  0) 0) |
| [104] |
Peigin S, Epstein B. Multipoint aerodynamic design of wing-body configurations for minimum drag[J]. Journal of Aircraft, 2015, 44(3): 971-980. (  0) 0) |
| [105] |
Peigin S, Epstein B. Computational fluid dynamics driven optimization of blended wing body aircraft[J]. AIAA Journal, 2006, 44(11): 2736-2745. DOI:10.2514/1.19757 (  0) 0) |
| [106] |
Epstein B, Peigin S. Efficient approach for multipoint aerodynamic wing design of business jet aircraft[J]. AIAA Journal, 2007, 45(11): 2612-2621. DOI:10.2514/1.29307 (  0) 0) |
| [107] |
Ernesto Benini, Rita Ponza, Andrea Massaro. High-lift multi-element airfoil shape and setting optimization using multi-objective evolutionary algorithms[J]. Journal of Aircraft, 2011, 48(2): 683-696. DOI:10.2514/1.C031233 (  0) 0) |
| [108] |
Andrea Massaro, Ernesto Benini. Multi-objective optimization of helicopter airfoils using surrogate-assisted memetic algorithms[J]. Journal of Aircraft, 2012, 49(2): 375-383. DOI:10.2514/1.C001017 (  0) 0) |
| [109] |
C.Comis Da Ronco, Rita Ponza, Benini E. Aerodynamic shape optimization of aircraft components using an advanced multi-objective evolutionary approach[J]. Comput. Methods Appl. Mech. Engrg, 2015, 285: 255-290. DOI:10.1016/j.cma.2014.10.024 (  0) 0) |
| [110] |
Obayashi S, Sasaki D, Takeguchi Y, et al. Multiobjective evolutionary computation for supersonic wing-shape optimization[J]. IEEE Transactions on Evolutionary Computation, 2000, 4(2): 182-187. DOI:10.1109/4235.850658 (  0) 0) |
| [111] |
Obayashi S. Pareto solutions of multipoint design of supersonic wings using evolutionary algorithms[M]. Adaptive Computing in Design and Manufacture V. Springer London, 2002:3-15. https://link.springer.com/chapter/10.1007/978-0-85729-345-9_1?no-access=true
(  0) 0) |
| [112] |
Leifur Leifsson, Slawomir Koziel, Yonatan A. Tesfahunegn, multiobjective aerodynamic optimization by variable-fidelity models and response surface surrogates[J]. AIAA Journal, 2016, 54(2): 531-541. DOI:10.2514/1.J054128 (  0) 0) |
| [113] |
Wang Rongwei, Gao Zhenghong. Improved multi-objective particle swarm optimization algorithm for aerofoil aerodynamic optimization design[J]. Chinese Journal of Applied Mechanics, 2011, 28(3): 232-236. (in Chinese) 王荣伟, 高正红. 基于改进粒子群算法的翼型多目标优化研究[J]. 应用力学学报, 2011, 28(3): 232-236. (  0) 0) |
| [114] |
Wang Chao, Gao ZhengHong. Refined aerodynamic design optimization of a wing with small aspect ratio[J]. Scientia Sinica Technologica, 2015, 06: 643-653. (in Chinese) 王超, 高正红. 小展弦比薄机翼精细化气动优化设计研究[J]. 中国科学:技术科学, 2015, 06: 643-653. (  0) 0) |
| [115] |
Li Quan, Guo Zhaodian, Lei Wutao, et al. Engineering environment-based multi-objective optimization platform for aerodynamic design[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(1): 255-268. (in Chinese) 李权, 郭兆电, 雷武涛, 等. 基于工程环境的气动多目标优化设计平台研究[J]. 航空学报, 2016, 37(1): 255-268. (  0) 0) |
| [116] |
Zhao Ke, Gao Zhenghong, Huang Jiangtao, et al. Aerodynamic optimization of rotor airfoil based on multi-layer hierarchical constraint method[J]. Chinese Journal of Aeronautics, 2016, 29(6): 1541-1552. DOI:10.1016/j.cja.2016.09.005 (  0) 0) |
| [117] |
Oliver Schutze, Adriana Lara, Carlos A. Coello coello, on the influence of the number of objectives on the hardness of a multiobjective optimization problem[J]. IEEE Transactions on Volutionary Computation, 2011, 15(4): 444-455. DOI:10.1109/TEVC.2010.2064321 (  0) 0) |
| [118] |
Taguchi G. Quality engineering through design optimization[M]. New York: Kraus Internatio-nal Publications, 1984.
(  0) 0) |
| [119] |
Huyse L, Lewis R M. Aerodynamic shape optimization of two-dimensional airfoilis under uncertain operating conditions[R]. NASA TM-CR-2001-210648, 2001.
(  0) 0) |
| [120] |
Li W, Huyse L, Padula S. Robust airfoil optimization to achieve drag reduction over a range of Mach numbers[J]. Structural and Multidisciplinary Optimization, 2002, 24(1): 38-50. DOI:10.1007/s00158-002-0212-4 (  0) 0) |
| [121] |
Huyse L, Padula S, Lewis R M, et al. Probabilistic approach to free-form airfoil shape optimization under uncertainty[J]. AIAA Journal, 2002, 40(9): 1764-1772. DOI:10.2514/2.1881 (  0) 0) |
| [122] |
Li W, Padula S. Using high resolution design spaces for aerodynamic shape optimization under uncertainty[R]. NASA, Technical Rept. TP-2004-213003, 2004.
(  0) 0) |
| [123] |
Wang Y, Yu X. Robust optimization of aerodynamic design using surrogate model[J]. Trans. of Nanjing University of Aeronautics and Astronautics, 2007, 24(3): 181-187. (  0) 0) |
| [124] |
Bai Junqiang, Wang Bo, Sun Zhiwei, et al. The research of robust supercritical airfoil design optimization[J]. Acta Aerodynamica Sinica, 2011, 29(4): 459-463. (in Chinese) 白俊强, 王波, 孙智伟, 等. 超临界翼型稳健型优化设计研究[J]. 空气动力学学报, 2011, 29(4): 459-463. (  0) 0) |
| [125] |
Huang Jiangtao, Gao Zhenghong, Zhao Ke, et al. Robust design of supercritical wing aerodynamic optimization considering fuse interfering[J]. Chinese Journal of Aeronautics, 2010, 23(5): 523-528. DOI:10.1016/S1000-9361(09)60250-8 (  0) 0) |
| [126] |
Li Jiaozan, Gao Zhenghong. Multi objective optimization methodology for airfoil robust design under geometry uncertainty[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 611-615. (in Chinese) 李焦赞, 高正红. 基于几何不确定性的翼型多目标稳健优化设计[J]. 力学学报, 2011, 43(3): 611-615. DOI:10.6052/0459-1879-2011-3-lxxb2010-066 (  0) 0) |
| [127] |
Li Jing, Gao Zhenghong, Huang Jiangtao, et al. Robust design of NLF airfoil[J]. Chinese Journal of Aeronautics, 2013, 26(2): 309-318. DOI:10.1016/j.cja.2013.02.007 (  0) 0) |
| [128] |
ZhaoKe, Gao Zhenghong, Huang Jiangtao. Robust design of natural laminar flow supercritical airfoil by multi-objective evolution method[J]. Applied Mathematics and Mechanics, 2014, 35(2): 191-202. DOI:10.1007/s10483-014-1783-6 (  0) 0) |
| [129] |
Zhao Ke, Gao Zhenghong, Huang Jiangtao, et al. Airfoil robust optimization based on polynomial chaos technique[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 10-19. (in Chinese) 赵轲, 高正红, 黄江涛, 等. 基于混沌多项式方法的翼型流场不确定性分析及稳健设计研究[J]. 力学学报, 2014, 46(1): 10-19. DOI:10.6052/0459-1879-13-127 (  0) 0) |
| [130] |
George R Anderson. Shape optimization in adaptive search spaces[D]. Ph. D. thesis, Stanford University, 2015. https://www.nas.nasa.gov/publications/ams/2015/09-29-15.html
(  0) 0) |
| [131] |
Jeong S, Chiba K, Obayashi S. Data mining for aerodynamic design space[J]. Journal of Aerospace Computing, Information and Communication, 2005, 2(11): 452-69. DOI:10.2514/1.17308 (  0) 0) |
| [132] |
Obayashi S, Sasaki D. Self-organizing map of Pareto solutions obtained from multiobjective supersonic wing design[R]. AIAA 2002-0991.
(  0) 0) |
| [133] |
Poole D J, Allen C B, Rendall C S. Metric-based mathematical derivation of efficient airfoil design variables[J]. AIAA Journal, 2015, 53(5): 1349-1361. DOI:10.2514/1.J053427 (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


