分离是常见而又复杂的流动现象。1904年Prandtl给出了二维不可压缩流绕固定平面上的分离点判据,1958年Moor、Rott和Sears提出了运动壁上判定流动分离的MRS准则,2005年张涵信院士对之前的判据进行总结,提出了三维可压缩非定常固定壁面分离的判据及理论[1]。对流动分离的判定在争议中发展了一个多世纪,对分离现象的准确模拟仍然是CFD面临的一项重要挑战。尤其是近年来全世界范围内掀起了高超声速飞行器[2-3]研制的热潮,在高超声速分离流动中出现的剪切层失稳、压力脉动、激波振荡、涡干扰等复杂现象,使得流动分离问题愈加复杂,流动分离对飞行器气动特性的影响变得不可回避而且愈加重要。
Post、Gaitonde、Nonomura等[4-6]通过等离子体激励器研究了翼型NACA0015的分离流动控制特性,发现满足一定参数条件下的射流可以增强掺混,抑制流动分离。Holden等[7-8]开展了高超声速双锥分离流动实验研究,获得了多个状态下准确的压力、热流分布数据。Candler、Druguet、Nompelis等[9-11]研究了高温真实气体效应、稀薄气体效应、网格收敛性及数值格式对双锥分离流动特性的影响。王兵、邓学蓥[12-13]采用细长旋成体与后掠翼的组合体模型,研究了前体分离流产生的非对称涡诱导机翼摇滚运动特性的影响。雷娟棉、吴甲生[14]等对旋转火箭弹的锥形运动与抑制进行了研究,指出单独的弹身旋转空气动力效应是由气流的粘性作用产生,与边界层性质、转捩、分离等密切相关。李晓东[15]、杨党国[16]等研究了超声速空腔流激振荡与声学特性,发现空腔内分离特性与激振频率存在对应关系。综上可知:1) 对流动分离的研究主要以简单外形和标准模型为主,对复杂外形和工程计算中的结果比较少见;2) 流动分离对流场特性如压力、热流分布的影响研究较多,而飞行高度、壁温、迎角等对流动分离的影响研究较少。基于此,本文尝试研究了类HTV-2高超声速飞行器体襟翼局部分离流动随飞行高度、壁温和迎角等因素的变化特性。
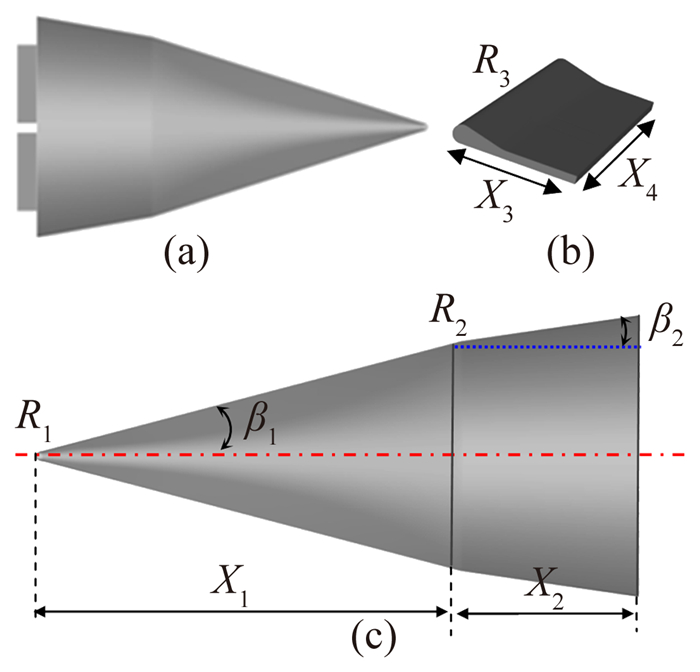
1 计算模型及方法由于真实的HTV-2外形数据无法获得,本文研究的类HTV-2外形是根据公开的HTV-2数据设计的,虽然与真实外形有一定差距,但它具有该类飞行器面对称、小控制舵面(体襟翼)等典型特征,计算模型如图(1)所示,其中(a)为装配示意图、(b)为体襟翼,(c)为未安置舵面的光滑外形,体襟翼在机身尾部呈对称型分布,间距100mm,超出机身长度为200mm。典型几何尺寸参数为:X1=2500mm,X2= 1200mm,R1= 7.5mm,R2= 900mm,β1=17.5°,β2=10°;X3= 500mm,X4=900mm,R3=50mm。
|
图 1 类HTV-2高超声速飞行器模型图 Figure 1 Flight vehicle model similar to HTV-2 |
本文数值模拟采用的计算方法以公式(1) 为控制方程,其中
计算坐标系下,三维非定常、可压缩、无量纲Navier-Strokes(N-S)方程具体形式如下:
| $ \frac{{\partial \hat Q}}{{\partial t}} + \frac{{\partial \left( {\hat F - {{\hat F}_V}} \right)}}{{\partial \xi }} + \frac{{\partial \left( {\hat G - {{\hat G}_V}} \right)}}{{\partial \eta }} + \frac{{\partial \left( {\hat H - {{\hat H}_V}} \right)}}{{\partial \zeta }} = 0 $ | (1) |
复杂的高超声速分离流动对于CFD数值模拟来说极具挑战,其中一个重要原因就是计算结果的网格依赖性非常强[18],即网格达到极密的情况下才能得到满足网格收敛性条件的流场解。本文采用三套疏密不同的15°襟翼偏角的全模网格来考察网格的收敛性:(1) coarse——稀网格811万,流向×法向×周向约为(下同):200×200×200;(2) medium——中等网格1872万:300×200×300;(3) fine——密网格3155万:400×200×400,法向网格均相同,保证壁面y+≤1。
图 2显示了中等规模网格壁面格点分布情况,网格采用标准多块结构对接形式,在上表面曲率变化较大的位置及缝处进行了加密处理以保证分离区流动的精细捕捉,网格总量约1872万,其上游距头部0.25L,下游距后缘2L,远场边界距中心线2.5L(L为全弹长度)。为提高并行计算效率,将网格分为376块,最大块网格量约8万,保证每个计算核心分配到大致相等的计算量。

|
图 2 网格收敛性验证采用的中等规模网格 Figure 2 Near wall mesh distribution of medium grid |
对三套网格在飞行高度H=55km、Ma=15、飞行迎角α=10°进行了对比计算,表 1为三套网格计算结果,可知coarse网格与fine网格阻力系数CA相差11.85%,升力系数CN相差3.77%,俯仰力矩系数Cm相差8.16%,而medium与fine网格计算结果吻合很好,我们认为medium网格达到了收敛性标准,以medium网格为基准,开展下面的对比工作。
| 表 1 网格无关性验证计算结果 Table 1 Grid independent verification |
|
|
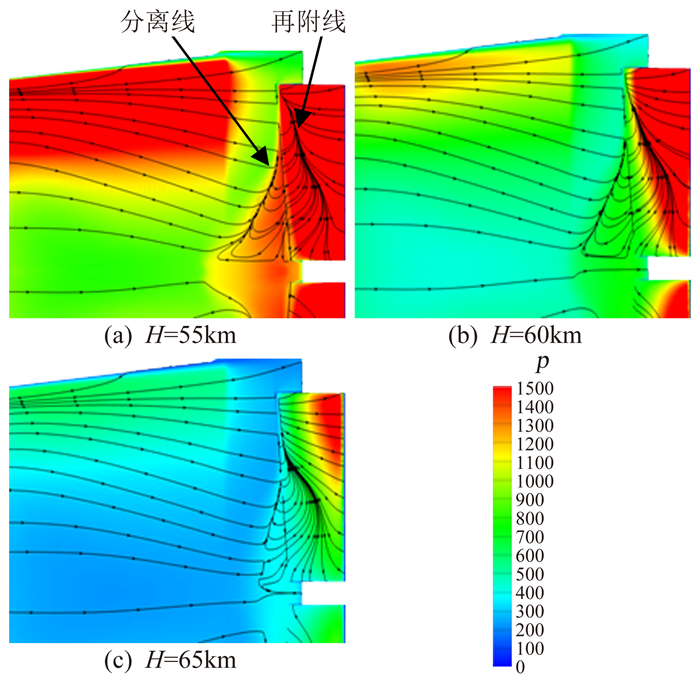
本文研究了飞行高度H在55km、60km和65km三种情况下体襟翼局部分离流动的差异。来流条件除了飞行高度不同外,其它参数完全相同,即马赫数Ma=15、飞行迎角α=10°、壁温Tw=1000K。图 3比较了体襟翼与飞行器表面的压力云图和极限流线分布,可以看到体襟翼上的压力明显高于上游的飞行器表面,于是沿流向形成了逆压梯度,从而导致了体襟翼与飞行器表面之间的压缩拐角发生了流动分离现象。分离发生在飞行器表面,而在体襟翼上流动再附,分离区在飞行器展向中心处最大,沿展向向外不断减小。
|
图 3 体襟翼与飞行器表面压力云图及极限流线分布(Ma=15,α=10°) Figure 3 Pressure contour and limiting streamlines at typical surface of body flap and flight vehicle (Ma=15, α=10°) |
平板边界层流动分离理论[19]表明,分离的发生取决于两个方面的因素:一个是逆压梯度的存在,是必要条件,但不是充分条件;另一个是前方来流边界层内的粘性力大小(速度梯度占主导),在存在逆压梯度的前提下由其决定分离是否发生。
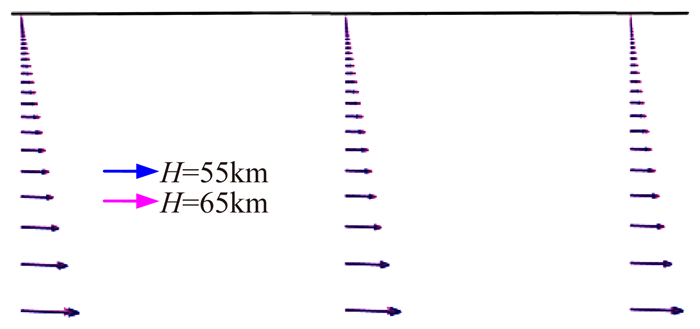
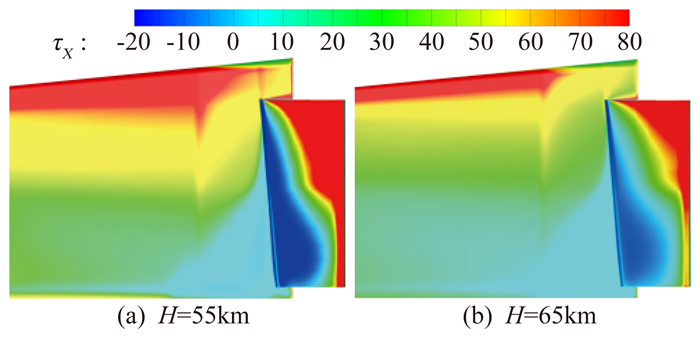
图 3中比较不同高度的结果发现,随着高度的增加分离点后移、再附点前移,使得整个分离区不断减小,表现为分离线向下游移动而再附线向上游移动,特别是位于展向中心位置的分离区随高度增加而减小的比较明显。比较图 3中压力分布发现,逆压出现位置随高度增加而后移,同时高度越高表面压力越低(来流压力随高度增加而降低所致),使得逆压梯度区的度量值越小,从而使流动更不易发生分离。另一方面,通过图 4不同高度下压缩拐角上游壁面流向速度分布可以发现,高度的改变对壁面速度梯度的影响不大,因此上游壁面粘性力在不同高度下差异不大(图 5)。由此,不同高度情况下逆压梯度对分离流动的差异起到了关键作用,即高度越高分离区越小。
|
图 4 压缩拐角上游平行流向截面的速度矢量图(Ma=15,α=10°) Figure 4 Velocity vector diagram at upstream section of compression corner(Ma=15, α=10°) |
|
图 5 体襟翼与飞行器表面粘性力分布图(Ma=15, α=10°) Figure 5 Friction distribution on typical surface of body flap and flight vehicle (Ma=15, α=10°) |
固定来流条件(H=60km,Ma=20,α=10°)下,研究了壁面温度差异对分离流动特性的影响。选取了三种壁温情况,分别为Tw=500K、1000K、1500K。图 6显示了体襟翼与飞行器表面压缩拐角附近的压力云图和极限流线分布,可以发现随壁温增加分离区逐渐增大,图中表现为分离线前移、再附线后移;而不同壁温情况下壁面的压力分布相差不大,即壁温的改变基本没有影响逆压梯度的特性。图 7(b)给出的分离核心区压力沿x方向的分布进一步证明了不同壁温下压力分布差异不明显。图 7(a)显示了在分离区上游壁面某位置流向速度沿壁面法向的分布,可以看到,壁温越高速度沿法向的梯度越小,实际上反映了当地摩擦力系数Cf的减小(图 7(c)),即流动附着能力的下降,因此更容易发生分离。
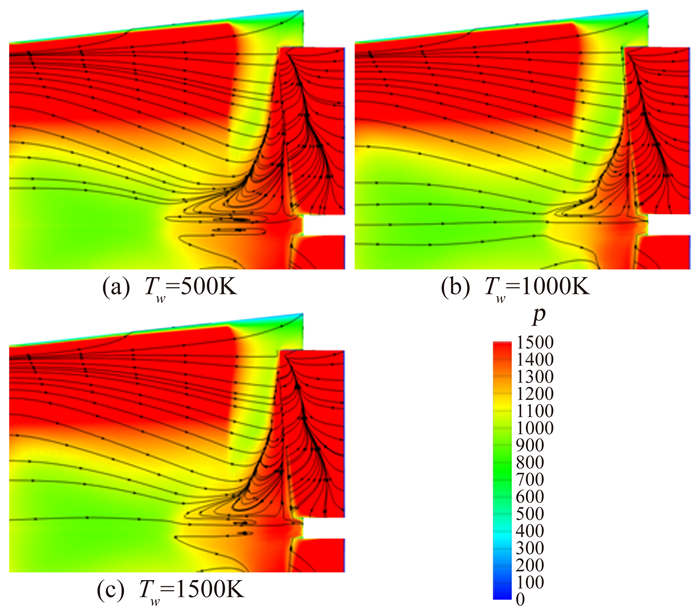
|
图 6 体襟翼与飞行器表面压力云图及流线分布(H=60km,Ma=20,α=10°) Figure 6 Pressure contour and limiting streamlines at typical surface of body flap and flight vehicle (H=60km, Ma=20, α=10°) |

|
图 7 Z1=100mm占位流场参数分布曲线图 Figure 7 Distribution curves of different flow field parameter on Z1 cross-section |
选取典型来流条件(H=60km,Ma=20,Tw=1000K),改变来流的迎角进行数值模拟,以研究迎角变化对分离特性的影响规律。分别模拟了三个迎角(α=5°、10°、15°)情况下的流场。图 8给出了不同迎角下体襟翼与飞行器表面压缩拐角附近Z1=100mm占位空间截面流场的压力云图及流线分布,可以看到迎角增加分离区逐渐减小。
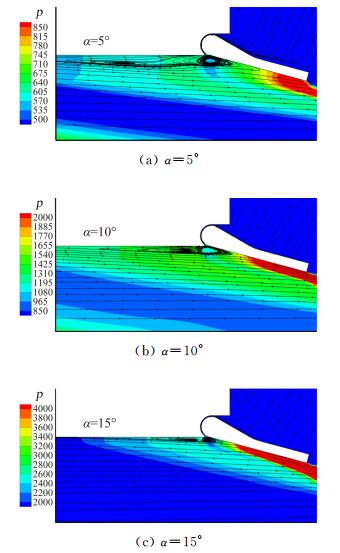
|
图 8 Z1占位空间截面流场的压力云图及极限流线分布(H=60km,Ma=20) Figure 8 Pressure contour and limiting streamlines at Z1 cross-section |
通过图 8中的压力分布可以看到,体襟翼与上游飞行器表面的逆压梯度区及梯度量值,随着迎角增加是不断增大的,通过图 9(a)壁面压力沿流向分布曲线更加清楚的获得了证明。图 9(b)给出了压缩拐角上游流动壁面某位置的流向速度沿壁面法向的分布,随着迎角增大,边界层厚度明显减小,速度梯度不断增大,这必然带来粘性力的增加,图 9(c)给出的壁面粘性摩阻系数分布证明了这一点。由于速度梯度增加带来的粘性力增大而阻碍流动分离的效果超过了逆压梯度增加促进流动分离的效果,从而使得分离区随迎角的增加反而不断减小。
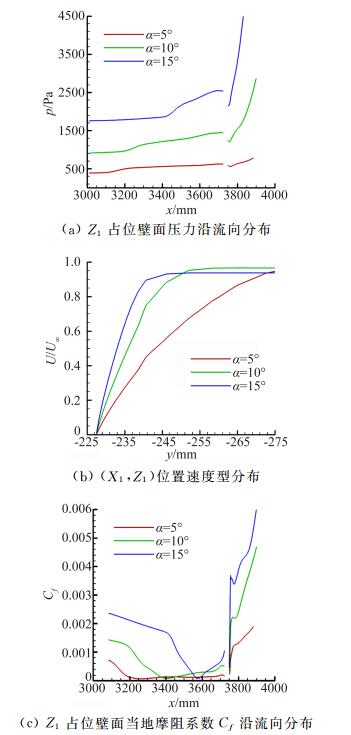
|
图 9 Z1占位流场参数分布曲线图 Figure 9 Distribution curves of different flow field parameter on Z1 cross-section |
本文采用基于全N-S方程的CFD数值模拟技术研究了类HTV-2高超声速飞行器在高空高速飞行环境下不同高度、壁温和迎角等参数对体襟翼局部流动分离的影响,通过分析获得如下一些结论:
1) 随高度增加,壁面压力分布发生改变,体襟翼与飞行器表面附近沿着流向所形成的逆压梯度减弱,使得压缩拐角内的流动分离区减小;
2) 壁面温度增加导致压缩拐角上游的流向速度梯度减小,即壁面粘性力减小,从而使分离区增大;
3) 随着迎角增加,压缩拐角内的逆压梯度增大,将使流动更容易发生分离,但上游流向速度梯度增加带来的粘性力增大更为明显,使得流动不容易发生分离的效果更强烈,从而分离区减小。
| [1] |
张涵信. 分离流与涡运动的结构分析[M]. 北京: 国防工业出版社, 2005.
(  0) 0) |
| [2] |
Leonard C P, Amundsen R M, Bruce Ⅲ W E. Hyper-X hot structures design and comparison with flight data[R]. AIAA 2005-3438, 2005.
(  0) 0) |
| [3] |
Rasky D J, Pittman R B, Newfield M E. The reusable launch vehicle challenge[R]. AIAA 2006-7208, 2006.
(  0) 0) |
| [4] |
Post M L, Corke T C. Separation control using plasma actuators-stationary and oscillatory airfoils[R]. AIAA 2004-0841, 2004.
(  0) 0) |
| [5] |
Gaitonde D V, Visbal M R, Roy S. Control of flow past a wing section with plasma-based body forces[R]. AIAA 2005-5302, 2005.
(  0) 0) |
| [6] |
Nonomura T, Aono H, Sato M, et al. Control mechanism of plasma actuator for separated flow around NACA0015 at Reynolds Number 63, 000 separation bubble related mechanisms[R]. AIAA 2013-0853, 2013.
(  0) 0) |
| [7] |
Holden M S, Wadhams T P. Code validation study of laminar shock/boundary layer and shock/shock interactions in hypersonic flows. Part A:experimental measurements[R]. AIAA 2001-1031, 2001.
(  0) 0) |
| [8] |
Holden M S. Experimental studies in LENS shock and expansion tunnel to examine real-gas effects in hypervelocity flows[R]. AIAA 2004-0916, 2004.
(  0) 0) |
| [9] |
Candler G V, Nompelis I, Holden M S. Computational analysis of hypersonic laminar viscous-inviscid interactions[R]. AIAA 2000-0532, 2000.
(  0) 0) |
| [10] |
Druguet M C, Candler G V, Nompelis I. Effect of numerics on Navier-Stokes computations of hypersonic double-cone flows[J]. AIAA Journal, 2005, 43(3): 616-623. DOI:10.2514/1.6190 (  0) 0) |
| [11] |
Nompelis I, Candler G V, MacLean M, et al. Numerical investigation of double-cone flow experiments with high-enthalpy effects[R]. AIAA 2010-1283, 2010.
(  0) 0) |
| [12] |
Deng X Y, Wang G, Chen X R, et al. A Physical model of asymmetric vortices flow structure in regular state over slender body at high angle ofattack[J]. Science in China (Series E), 2003, 43(6): 561-573. (  0) 0) |
| [13] |
Wang B, Deng X Y, Ma B F, et al. Effect of tip perturbation and wing locations on rolling oscillation induced byforebody vortices[J]. Acta Mech. Sinica, 2010, 26: 787-791. DOI:10.1007/s10409-010-0358-z (  0) 0) |
| [14] |
Lei Juanmian, Wu Jiasheng. Coning motion and restrain of large fineness ration unguided spinning rocket stabilized with tail fin[J]. Acta Aerodynamica Sinica, 2005, 23(4): 455-457. (in Chinese) 雷娟棉, 吴甲生. 尾翼稳定大长径比无控旋转火箭弹的锥形运动与抑制[J]. 空气动力学学报, 2005, 23(4): 455-457. (  0) 0) |
| [15] |
Li Xiaodong, Liu Jingdong, Gao Junhui. Numerical simulation of flow-induced oscillation and sound generatino in a cavity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 599-604. (in Chinese) 李晓东, 刘靖东, 高军辉. 空腔流激振荡发声的数值模拟研究[J]. 力学学报, 2006, 38(5): 599-604. (  0) 0) |
| [16] |
Yang Dangguo, Fan Zhaolin, Li Jianqiang, et al. Studies on flow characteristics of cavity by numerical simulation and wind tunnel test[J]. Acta Aerodynamica Sinica, 2008, 27(3): 378-383. (in Chinese) 杨党国, 范召林, 李建强, 等. 弹舱流动特性数值模拟及风洞试验研究[J]. 空气动力学学报, 2008, 27(3): 378-383. (  0) 0) |
| [17] |
Shi Lei, Yan Ming, Yang Yunjun, et al. Applicability investigation about several common schemes and turbulence models in high speed flow[J]. Journal of Aerospace Power, 2014, 29(8): 1904-1911. (in Chinese) 石磊, 闫溟, 杨云军, 等. 几种常用格式和湍流模型在高速流动中的适用性研究[J]. 航空动力学报, 2014, 29(8): 1904-1911. (  0) 0) |
| [18] |
Roy C J, Gallis M A, Bartel T J, et al. Navier-Stokes and direct simulation Monte Carlo predictions for laminar hypersonic separation[R]. AIAA 2001-1024, 2001.
(  0) 0) |
| [19] |
H.史里希廷. 边界层理论[M]. 北京: 北京科学出版社, 1991, 146-148.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35

