高超声速再入飞行器面临严酷的气动加热环境, 主要包括对流加热和辐射加热。通常情况下辐射加热可以忽略, 但以第二宇宙速度返回、部分具有低空高速特征的再入飞行器的辐射加热不能忽视, 这两类再入飞行器的辐射加热对热防护设计具有重要的影响。以探月及星际返回器为代表的各类地球大气再入飞行器在再入过程中,辐射加热和对流加热的重要性随着飞行速度的变化而变化,一般认为当飞行速度高于9km/s时,头部激波层气体变成对飞行器加热的强辐射体,辐射加热随着速度的增加才逐渐变得重要起来,辐射加热的峰值时刻所对应的高度一般在60km附近[1-6]。以飞船、航天飞机、X-37B为代表的再入飞行器再入速度较低(低于9km/s),在高空经过减速后在低空阶段速度也较低,如航天飞机在50km的高度速度降低至马赫数10以下,这类飞行器的辐射加热不明显[7]。但是以战略导弹为代表的高超声速再入飞行器和以HTV-2为代表的新型临近空间滑翔高超声速飞行器低空再入过程中,虽然再入速度低于9km/s,但由于再入过程中在低于30km的低空稠密大气层内,在导弹头部形成的高温激波层成为对导弹头部加热的强辐射体,辐射加热比较明显,局部弹道点位置、辐射加热达到对流加热的20%左右,辐射加热成为导弹头部热防护设计需要考虑的重要因素。
高超声速飞行器辐射加热的计算方法目前主要有工程计算方法和数值计算方法。国内外的研究人员针对再入高超声速飞行器的辐射特性开展了研究[8-9]。NASA开发了针对地球大气再入的辐射加热工程预测软件QRAD[2]。国内的董士奎[8]等开展了高超声速再入体可见、红外辐射特性数值模拟研究,通过数值求解化学非平衡流场和辐射传输方程,获得了高超声速再入体的辐射强度场。张志成[9]等开展了再入飞行器目标特性研究,对典型再入飞行器的红外辐射特性进行了数值模拟,获得了高温气体辐射特性结果。
上述研究未针对低空阶段(50km以下)再入时高温气体对飞行器头部的辐射加热、不同光谱带的加热特性及影响因素进行研究。本文则针对这些内容开展了重点研究。研究所用的方法是基于多光谱带模型的辐射加热工程计算方法[1],该方法综合考虑了非绝热效应、三维效应及非平衡效应等各种影响。
1 计算方法及模型计算模型为一维绝热平衡空气加热计算模型,计算方法采用文献[1]中的计算方法,该方法有效性在文献[1]中进行了验证,考虑了非平衡辐射加热及其“截断效应”[2],考虑了三维效应的影响。
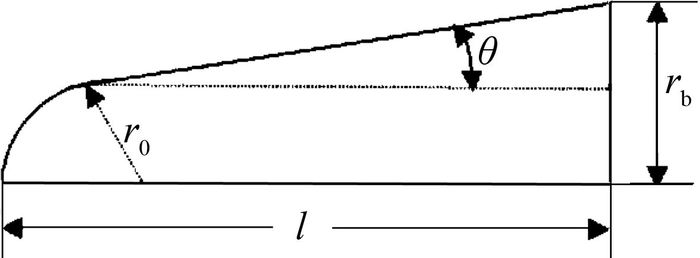
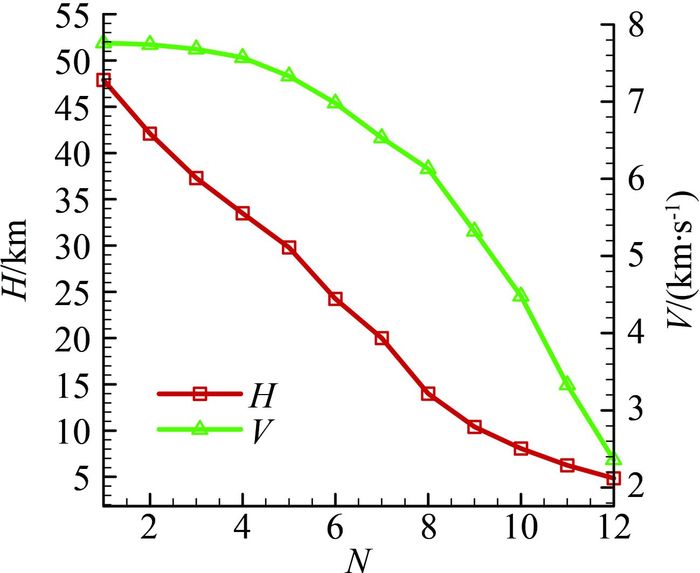
针对某典型再入导弹的轴对称球锥形飞行器开展了计算,飞行器头锥外形如图 1所示,飞行器头部的球头半径为0.137m。再入弹道如图 2所示,给出了12个飞行状态的弹道点。
|
| 图 1 再入体形状 Fig. 1 Shape of reentry body |
|
| 图 2 再入弹道示意图 Fig. 2 Trajectory of hypersonic reentry vehicle |
2 计算结果及分析 2.1 驻点热流计算结果
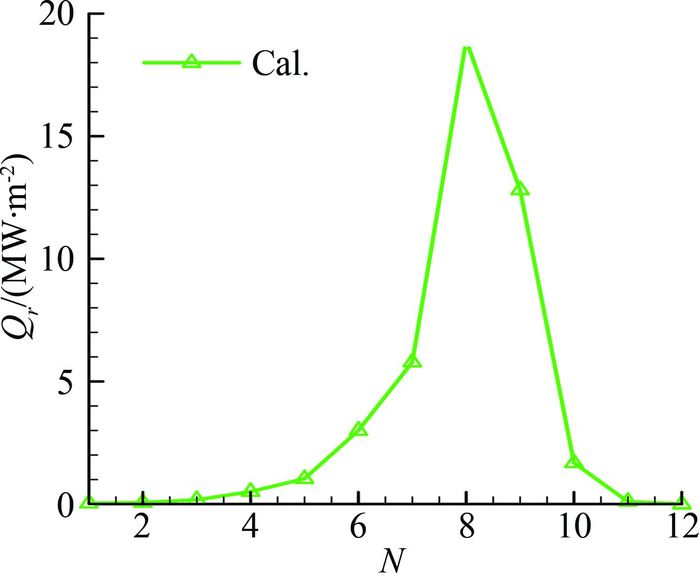
采用工程计算方法针对第1节中的计算模型开展了驻点辐射加热的计算。图 3为飞行器驻点辐射热流的分布,计算数据采用辐射加热工程计算方法获得。可以看出计算辐射加热峰值为18886kW/m2,对应的高度为14.0km,速度为6.1km/s,峰值热流出现在30km以下的稠密大气再入阶段。
|
| 图 3 驻点辐射热流计算数据 Fig. 3 Radiation heating flux at stagnation point |
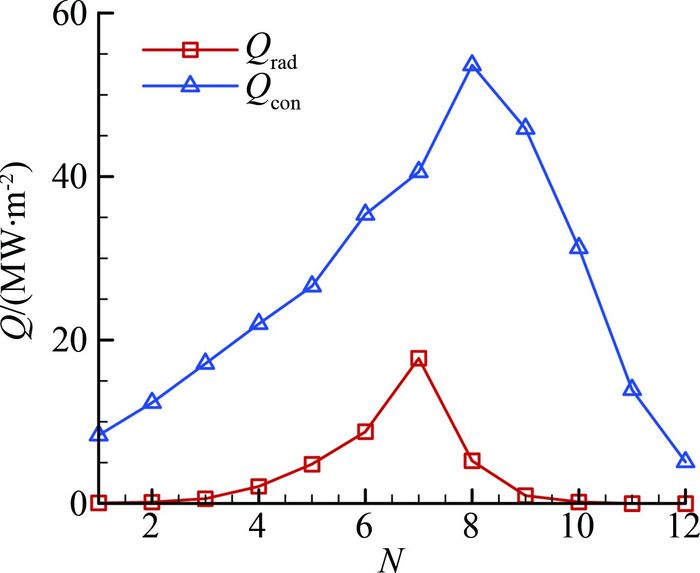
图 4为飞行器驻点辐射加热和对流加热的对比,对流热流采用文献[10]中的计算方法计算获得。整体上对流加热明显高于辐射加热,但在局部弹道点,辐射加热和对流加热相比占有明显的比例。
|
| 图 4 飞行器驻点辐射加热和对流加热的对比 Fig. 4 Comparison between stagnation-point radiation heating flux and convection heating |
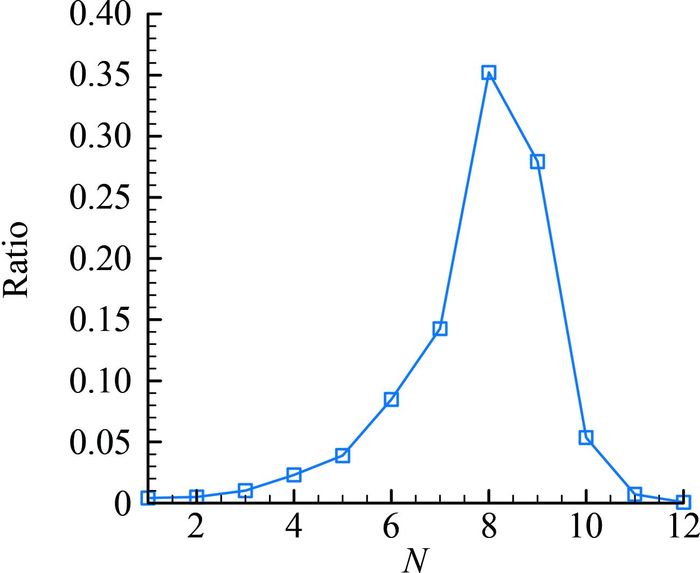
图 5为辐射加热和对流加热的比值。大部分时刻辐射加热所占的比例较小,在进入低空的稠密大气层后,辐射加热增强,局部时刻辐射加热占对流加热的30%左右。在弹道末端,随着飞行速度的下降,辐射加热重新减弱。
|
| 图 5 飞行器驻点辐射加热和对流加热的比值 Fig. 5 Ratio of stagnation-point radiation heating flux to convection heating |
2.2 不同光谱带的辐射加热特性
在低空再入阶段,不同光谱带的辐射特性不同,以可见连续谱带的辐射为主,其他光谱带的辐射较小。这和文献[1]中的高空再入阶段辐射加热特性有明显的不同。
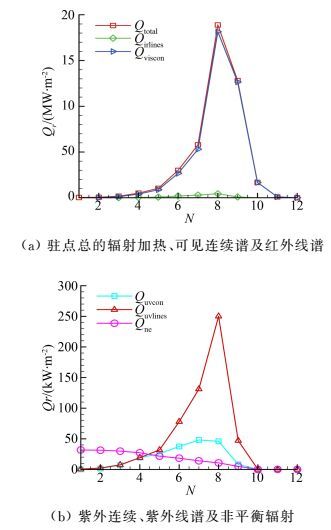
图 6为飞行器沿轨道的辐射加热及不同光谱带的辐射加热。在高度为14.0km、速度为6.1km/s弹道时刻,可见连续谱辐射加热为18142.4kW/m2,红外线谱辐射加热约为437.3kW/m2,紫外连续谱的辐射加热约为45.9kW/m2,其次为紫外线谱的辐射加热为250.0kW/m2,非平衡辐射为10.6kW/m2。
|
| 图 6 高超声速再入飞行器辐射加热计算结果 Fig. 6 Radiation heating flux of hypersonic reentry vehicle |
2.3 球头辐射加热分布特性
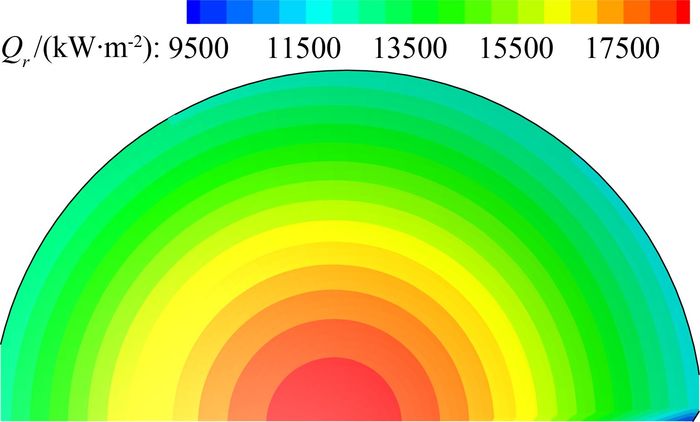
针对球头外形的飞行器端头开展了0°攻角状态下的辐射加热分布特性研究。球冠半角取31°。图 7为辐射峰值热流时刻(14km,6.1km/s)球头表面各个位置的辐射加热分布。可以看出,球头驻点部位的辐射加热最大,从球头驻点部位到球头边缘,辐射加热逐渐降低。
|
| 图 7 基于牛顿压力分布特性的球头辐射加热分布 Fig. 7 Radiation heating distribution based on newton methods |
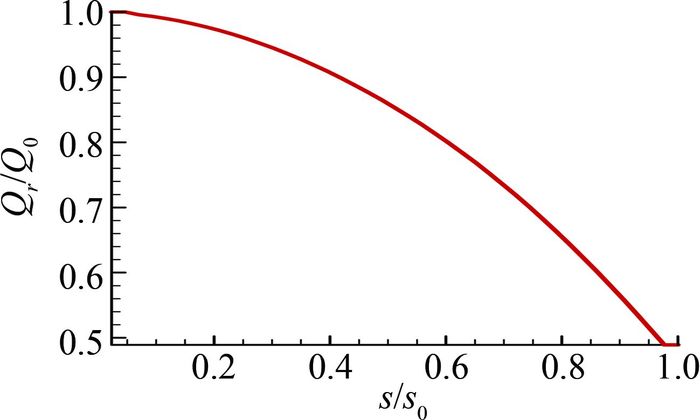
图 8为球头驻点至球头外边缘的辐射加热热流与几何驻点中心的辐射加热热流比值,横坐标为离开球头几何驻点中心的路径距离与球头至球头边缘路径距离的比值。可以看出,沿物理驻点至大底拐角,辐射加热逐渐降低,在球头边缘处,辐射加热约为驻点辐射加热的50%。
|
| 图 8 球头辐射加热分布特性曲线 Fig. 8 Radiation heating distribution along centerline |
2.4 辐射加热影响参数分析 2.4.1 头部半径对辐射加热的影响规律
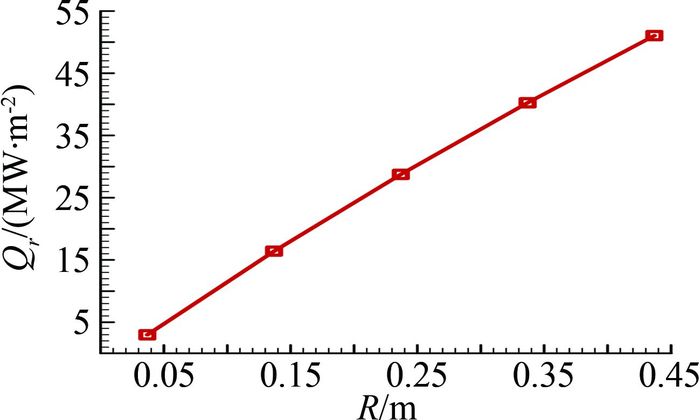
球头外形的高超声速飞行器头部半径对辐射加热具有明显的影响。图 9为在高度14km、速度6.1km/s的典型飞行状态下,辐射热流随球头半径变化的影响规律。随着球头半径的增加,辐射加热逐渐增大。
|
| 图 9 球头驻点辐射加热随球头半径变化 Fig. 9 Radiation heating via radius |
2.4.2 飞行高度对辐射加热的影响规律
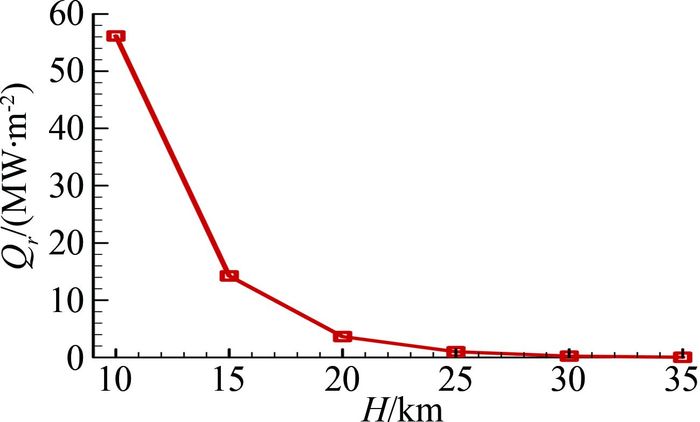
高超声速飞行器的飞行高度对辐射加热具有明显的影响。图 10为在球头半径0.137m、速度6.1km/s的典型飞行状态下,辐射热流随飞行高度变化的影响规律。随着飞行高度的降低,辐射加热逐渐增大。高度超过30km以后,辐射加热明显减弱。
|
| 图 10 球头驻点辐射加热随飞行高度变化 Fig. 10 Radiation heating via height |
2.4.3 飞行速度对辐射加热的影响规律
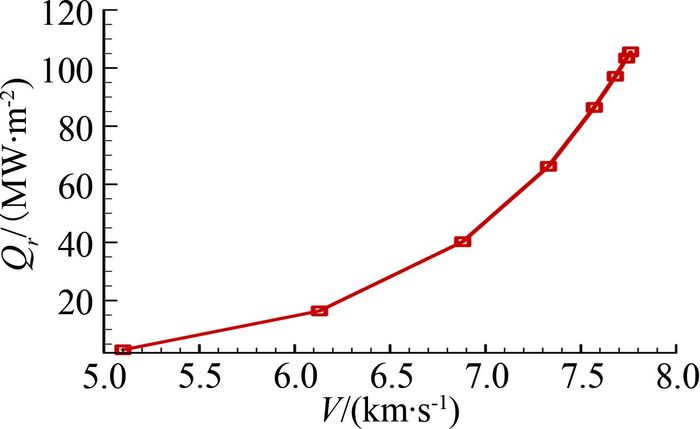
高超声速飞行器的速度对辐射加热具有明显的影响。图 11为在球头半径0.137m、高度14km的典型飞行状态下,辐射热流随速度的影响规律。随着飞行速度的增加,辐射加热逐渐增大。
|
| 图 11 球头驻点辐射加热随飞行速度变化 Fig. 11 Radiation heating via velocity |
3 结论
本文针对高超声速飞行器的辐射加热特性开展了计算研究,通过计算结果与飞行试验数据对比,表明计算结果的可靠性较高。基于高温平衡空气的四光谱带模型,并综合考虑了三维效应及非平衡效应等各种影响,计算结果表明:
1) 所采用的计算方法可以准确地预测高超声速飞行器的辐射加热。高超声速飞行器在低空高速飞行阶段,由于低空大气密度较大,辐射加热效应比较明显,局部时刻占到对流加热的17%左右,热防护设计时需要考虑。
2) 和探月返回器的辐射加热不同,以战略导弹为代表的高超声速再入飞行器和各类临近空间高超声速飞行器的辐射加热峰值点位置高度较低,一般在30km以下,对应的飞行速度也较低。
3) 从辐射加热的光谱分布特性看,高超声速飞行器主要由可见连续谱构成,红外线谱和紫外线谱的辐射加热也比较明显,紫外连续谱的辐射加热较弱。由于辐射加热主要发生在大气层低空区域,非平衡辐射加热也比较弱,可以忽略不计。
4) 高超声速飞行器的辐射加热随着球头半径的增加而增大,随着高度的增加而降低,随着速度的增大而增大。
| [1] |
Chen S Y, Miao W B, Cheng X L. The radiation heating calcu-lation method study of earth atmosphere reentry vehicle[J].
Acta Aerodynamica sinica, 2013, 31(3): 333–337.
(in Chinese) 陈思员, 苗文博, 程晓丽. 地球大气再入返回器辐射加热计算方法研究[J]. 空气动力学学报, 2013, 31(3): 333–337. |
| [2] | Ried R C, Jr Rochelle W C, Milhoan J D. Radiative heating to the apollo command module: engineering prediction and flight measurement[R]. NASA TM-X-58091, 1972. |
| [3] | Page W A, Compton D L, Borucki W J, et al. Radiative transport in inviscid nonadiabatic stagnation-region shock layers[R]. AIAA 1968-784. |
| [4] | Suttont T K. Stagnation-point radiative heating relations for earth and Mars entries[J]. Journal of Spacecraft and Rockets, 1991, 28(1): 40–42. DOI:10.2514/3.26206 |
| [5] | Park C. Radiation enhancement by non equilibrium in Earth's atmosphere[J]. Journal of Spacecraft and Rockets, 1985, 22(1): 1–13. DOI:10.2514/3.55545 |
| [6] | Wick B H. Radiative heating of vehicles entering the Earth's atmosphere[R]. NANA TM-X-56778, 1965. |
| [7] | Mikula D F K, Mark H, Todd J, et al. X-37 flight demonstrator system safety program and hallenges[R]. AIAA 2000-5073. |
| [8] |
Dong S K, Tan H P, He Z H, et al. Numerical simulation of visible and infrared radiation properties of hypersonic reentry bodies[J].
J Infrared Millim Waves, 2002, 21(3): 180–184.
(in Chinese) 董士奎, 谈和平, 贺志宏, 等. 高超声速再入体可见、红外辐射特性数值模拟[J]. 红外与毫米波学报, 2002, 21(3): 180–184. |
| [9] |
Zhang Z C, Gao T S, Dong W Z, et al. Study on modeling of reentry vehicle signatures[J].
Journal of Experiments in Fluid Mechanics, 2007, 21(1): 7–12.
(in Chinese) 张志成, 高铁锁, 董维中, 等. 再入飞行器目标特性建模研究[J]. 实验流体力学, 2007, 21(1): 7–12. |
| [10] | Tauber M E. A review of high-speed, convective, heat-transfer computation methods[R]. NASA TP-2914. |



