随着高空无人机、微小型飞行器等的迅速发展和应用, 低雷诺数流动已逐渐成为研究者关注的热点问题[1-2]。低雷诺数下, 层流态边界层抵抗逆压梯度的能力弱, 流动易发生分离, 由此对翼型的气动性能产生显著影响, 其具体表现为:升力减小而阻力增大, 升阻比骤降, 严重时甚至导致失速, 给飞行器的性能和稳定性带来了极大的挑战, 因此, 探讨低雷诺数下翼型流动分离的物理机制, 对于控制分离进而改进飞行性能有着重要的意义。
国内外研究者针对这一问题开展了许多工作并取得了很大的进展。Brendel和Mueller[3]早年间即对某翼型表面的分离泡进行了实验测量,发现转捩雷诺数随分离点动量厚度雷诺数的增加而增长;Hu和Yang[4]使用PIV技术对不同迎角下层流分离泡非定常流动结构的演化进行了分析;吴鋆等[5]结合氢气泡流动显示和PIV测速总结了翼型分离流结构随迎角的变化规律;Yarusevych等[6]综合烟线流动显示等方法对不同雷诺数下的翼型分离流动进行了细致分析;Buchmann等[7]则用实验验证了前缘零质量射流对大迎角分离的控制能力。数值计算方面,白鹏等[8]对不同雷诺数和迎角的E387翼型进行了二维模拟,研究了层流分离的非定常和时均特性;Catalano和Tognaccini[9]使用改进的SST模型对SD7003翼型分离流动进行计算,得到了较好的结果;Zhang等[10]对雷诺数10 000的两种翼型进行直接数值模拟,分析了几何参数变化对分离和转捩过程的影响;Visbal和Orkwis[11]评估了有无亚格子模型对隐式大涡模拟方法 (ILES) 预测低雷诺数流动的影响;Lee等[12]对低雷诺数下的NACA 0012翼型分别进行了层流、RANS和ILES计算,分析了三种方法在不同雷诺数和迎角下的预测能力;Gross和Fasel[13]采用混合湍流模型对部分失速的翼型绕流进行研究,发现通过合理调整可以达到较好的预测精度;王林等[14]采用数值方法研究了合成双射流对翼型分离流的控制效果;刘沛清等[15]则开展了不同吹/吸气参数对层流分离泡影响规律的数值分析。
尽管相关工作大量存在,但仍未能完全揭示翼型分离流动的物理机制,采用更高精度的数值方法对其开展研究显然是一条可行的途径。本文以Yarusevych等[6]的实验工作为参考,采用大涡模拟方法对来流迎角5°、马赫数0.4、三种雷诺数 (55000、100000和150000) 下的NACA0025翼型进行细致模拟,在此基础上分析雷诺数对分离流态的影响,其中Ma和Re均基于无穷远来流参数定义,参考长度取翼型弦长,后文展示的也是无量纲化之后的结果。
1 数值方法和程序验证计算工作使用叶建[16-17]发展的大涡模拟程序MPLES进行,该程序能够处理任意界面匹配的多块结构化网格,通过计算域分解和消息传递接口 (MPI) 实现并行,具有很高的计算效率。程序求解Favre滤波的无量纲化可压缩N-S方程组,其具体形式如下:
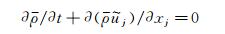
|
(1) |
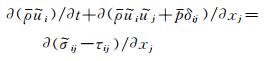
|
(2) |
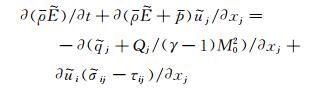
|
(3) |
要封闭上述方程组,必须对亚格子应力和亚格子热通量进行模化,这里选用如下形式的动力涡粘模型:
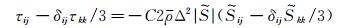
|
(4) |
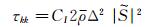
|
(5) |
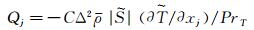
|
(6) |
其中的系数CI、C和PrT通过公式动态计算:
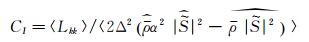
|
(7) |
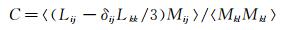
|
(8) |
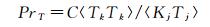
|
(9) |
上述各项的具体含义参见文献[16],这里不再一一列出。将封闭的方程组 (1~3) 写成积分形式,采用网格中心的有限体积法离散。对流项使用四阶反对称型的中心格式,粘性项使用二阶中心格式,时间推进则是三阶三步的紧致Runge-Kutta方法。为消除因对流项的中心型格式而在流场中出现的非物理振荡,还使用11点的显式选择性滤波器对流场变量进行滤波处理,相关细节见文献[17]。
考虑到Yarusevych等[6]实验和计算工况的马赫数不同,为进一步确认程序对翼型分离转捩流动的预测能力,首先对文献[18]的DNS算例进行模拟。该算例为迎角5°的NACA0012翼型,马赫数0.4、雷诺数50000,这里的LES与原文的DNS相比,计算域尺寸完全相同,网格均为C型网格,后者的网格数量高达17073万,而前者仅514万。
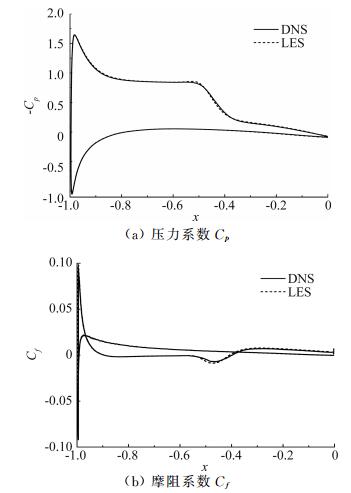
图 1给出了时均流场中翼型表面压力系数和摩阻系数的对比,虚线表示LES结果,实线为DNS数据[18]。从图 1(a)看,二者表面压力系数的分布几乎完全重合,压力平台暗示翼型上表面存在层流分离泡;从图 1(b)看,二者壁面摩阻系数的曲线也吻合得很好,预测的分离泡长度只有微小差异。可以预期,本文使用的LES程序对翼型分离流动的预测精度较高,下文针对NACA 0025翼型的仿真结果是可信的。
|
| 图 1 翼型表面压力与摩阻系数对比 Fig. 1 Comparison of pressure and skin friction coefficient |
2 NACA 0025翼型仿真 2.1 算例设计
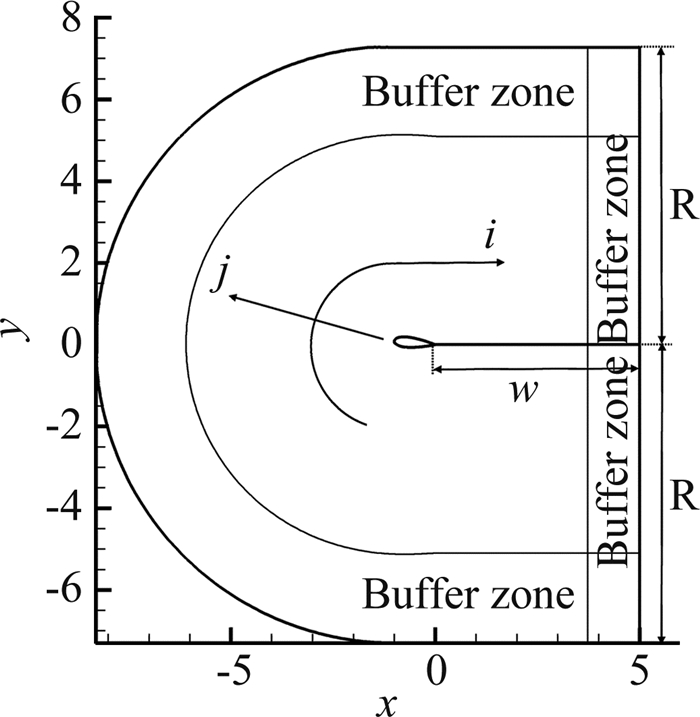
使用上述程序对来流迎角5°、马赫数0.4、雷诺数分别为55000、100000和150000的NACA 0025翼型进行仿真。计算域如图 2所示,以0°迎角时翼型的尾缘点为坐标原点,x、y、z分别代表流向、横向和展向。xy平面内,计算域入口段为半径7.3的半圆弧,横向边界距x轴±7.3,计算域出口位于x=5.0位置,三个算例的展向宽度不同,分别为0.4、0.19和0.16。计算网格为C型的结构化网格,展向均为64个单元,总的网格数分别约800万、1500万和1900万。以壁面粘性单位度量,第一层网格高度 (Δy+) 均不超过1,流向长度 (Δx+) 不超过31,展向宽度 (Δz+) 不超过16,三个算例的网格质量较高,完全符合大涡模拟的要求。
|
| 图 2 计算域示意图 Fig. 2 Computational domain |
边界条件的设置如下:翼型表面为绝热的无滑移壁面,所有外边界 (半圆弧进口、横向和出口) 均定义为远场边界,采用文献[19]的特征边界条件处理,展向则使用周期性边界条件。考虑到远场边条处理带来的误差可能发生反射污染内部流场,沿着整个外边界均设置了数层网格的缓冲区,吸收数值反射波。计算依托国家超算天津中心的天河-1A系统完成,根据需要,三个算例分别使用160、248、320个核心并行。
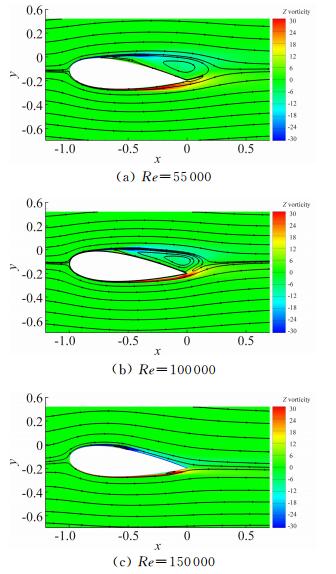
2.2 时均流场图 3为三种工况下时均流场的展向涡量-流线图。从图中可以看到,三种工况的翼型上表面均出现了分离流动,这是层流边界层受逆压梯度作用的结果;对比发现,Re=55000和100000时,时均流场的翼面上方出现开式分离且随着Re增大其尺寸有所减小,当Re=150000时,则形成时均化的闭式分离泡,其尺寸远小于前两种工况。
|
| 图 3 时均流场的展向涡量-流线图 Fig. 3 Spanwise vorticity and streamline of time averaged flowfield |
图 4为三种工况下翼型表面压力系数Cp分布的对比,容易看到,Re=55000和100000的曲线较为接近,Re=150000与二者差别很大。出现这种差异的原因和翼型表面的分离流态相关,从前缘滞止点开始,压力逐渐降低,在上下表面分别达到其最小值,而后压力升高,上下表面均受到逆压梯度作用,且上表面的数值更大。雷诺数较低时,上表面出现开式分离,压力到尾缘都无法恢复,由此翼型的升力很小。比较Re=55000和100000工况,雷诺数增加后,分离区有所减小,升力也稍有增大。雷诺数为150000时,时均化的开式分离区变为闭式分离泡,Cp曲线有了显著变化,从图中还可以看到,上下表面均有压力平台,这意味着两个表面都有分离。
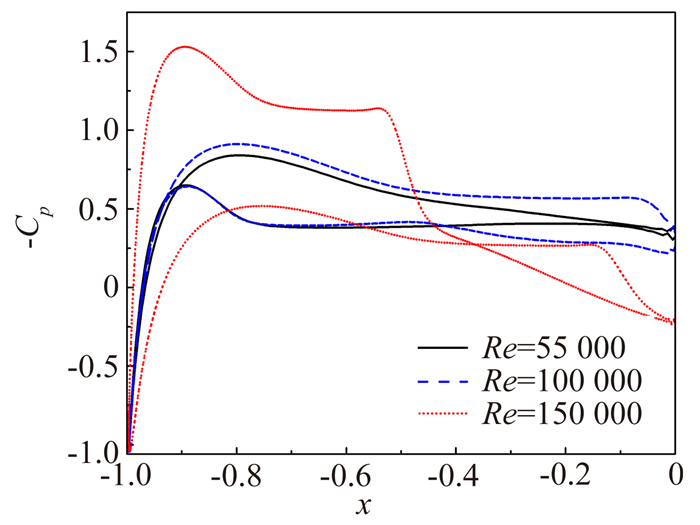
|
| 图 4 压力系数对比 Fig. 4 Comparison of pressure coefficient |
图 5给出了上表面摩阻系数的对比,从图中可以看出,Re=150000分离点位置较Re=55000和100000靠后,雷诺数较低时,流动为开式分离,不发生再附;Re=150000时,流动在x/c=-0.78处分离,而后又在x/c=-0.46处再附,形成经典的时均化闭式分离泡。
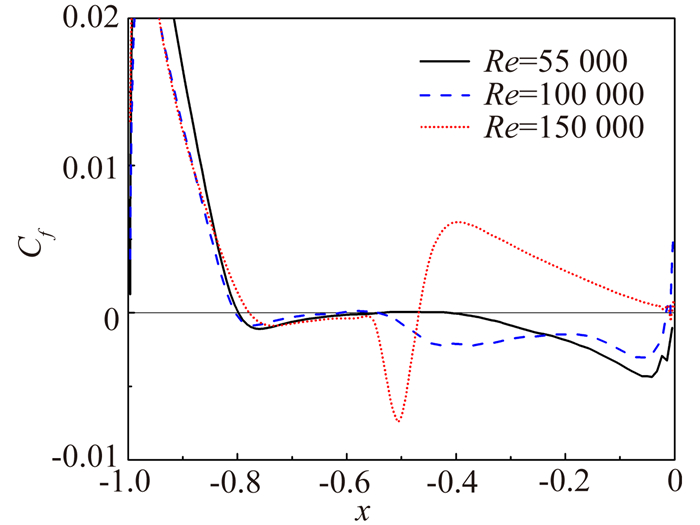
|
| 图 5 吸力面摩阻系数对比 Fig. 5 Comparison of skin friction coefficients of suction surface |
图 6为尾迹区不同流向位置的速度剖面,可以看到,随着尾迹向下游发展,尾迹区的速度亏损均趋于平缓,这是脱落的旋涡与主流之间、旋涡之间相互作用不断耗散的结果。Re=55000和100000形成宽的尾迹,Re=150000的尾迹宽度和速度亏损均有明显减小,由此说明时均化开式分离区的损失远大于闭式分离泡。
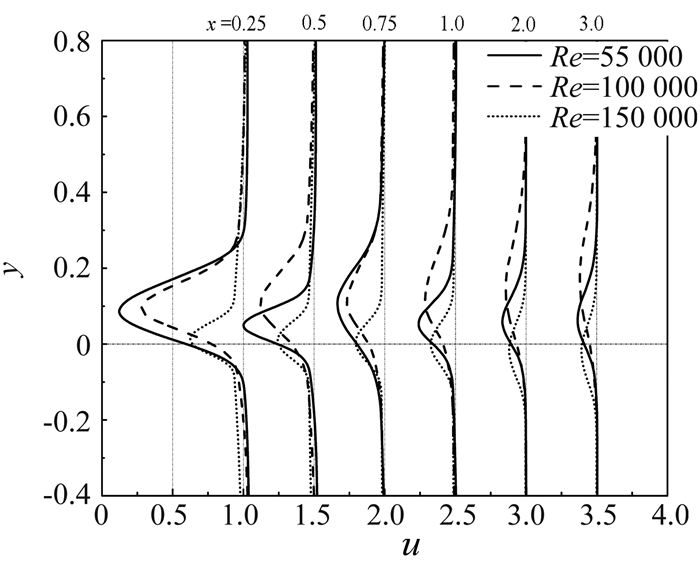
|
| 图 6 时均尾迹区速度剖面对比 Fig. 6 Comparison of time averaged wake velocity profile |
2.3 二阶统计量
图 7给出了流场二阶统计量 (雷诺应力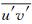
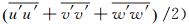
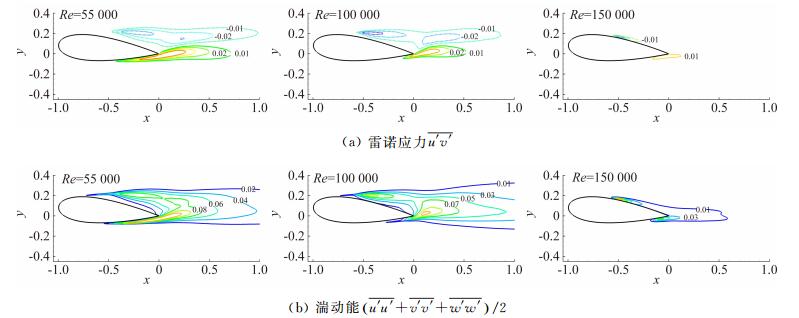
|
| 图 7 二阶统计量对比 Fig. 7 Comparison of second order statistics |
2.4 瞬态流场
图 8直观展现了三种工况下不同的三维流动结构,Re=55000和100000发生开式分离,形成大尺度的涡结构,向下游发展过程中,涡结构相互作用、破裂,最终演化为大尺度的尾迹区扰动;雷诺数为150000时,流动结构明显变小,涡结构沿着壁面向下游运动并最终脱落,形成扰动较为强烈的尾迹区。无论哪个工况,分离的初始阶段都可以看到明显的二维展向涡结构,其形成起源于自由剪切层的无粘不稳定性,这表明K-H不稳定性对层流分离诱导转捩过程起重要作用,但同时已有的大量研究表明,低雷诺数带来的粘性效应、近壁面对分离流动的制约、回流区的复杂扰动等因素对该过程也有重要影响,其中的流动机理有待进一步的深入探讨。
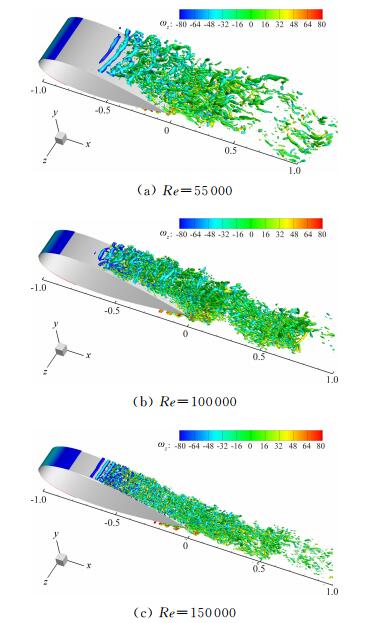
|
| 图 8 瞬态三维流场中的涡结构,旋涡识别Q准则 (Q=300,展向涡量着色) Fig. 8 Vortex structures of 3-D instantaneous flowfield (isosurface of Q at Q=300, colored by spanwise vorticity) |
3 结论
采用高精度大涡模拟方法对马赫数0.4、迎角5°、雷诺数55000、100000和150000下的NACA0025翼型进行仿真,对比分析雷诺数对层流分离流动的影响。
1) 数值验证表明,LES与DNS结果吻合很好,说明对于低雷诺数翼型绕流问题而言,本文所用程序能够很好地描述分离转捩流动。
2) 随着雷诺数的增加,分离流呈现两种不同的流态,Re=55000和100000时,翼型上表面发生大尺度的开式分离,形成宽的尾迹区;Re=150000时,分离后的自由剪切层再附到翼型表面,形成时均化的闭式分离泡,尾迹区宽度明显减小。
致谢: 特别感谢英国Southampton大学Sandham教授提供用于验证程序的DNS数据;本文绝大部分计算工作在国家超级计算天津中心的天河一号系统上完成,感谢天津中心提供的超算资源及相关技术支持。| [1] | Shyy W, Lian Y, Tang J, et al. Aerodynamics of low Reynolds number flyers[M]. New York: Cambridge University Press, 2008. |
| [2] |
Li F, Bai P, Shi W, et al. Low Reynolds number aerodynamics of micro air vehicles[J].
Advances in Mechanics, 2007, 37(2): 257–268.
(in Chinese) 李锋, 白鹏, 石文, 等. 微型飞行器低雷诺数空气动力学[J]. 力学进展, 2007, 37(2): 257–268. DOI:10.6052/1000-0992-2007-2-J2006-134 |
| [3] | Brendel M, Mueller T J. Boundary-layer measurements on an airfoil at low Reynolds numbers[J]. Journal of Aircraft, 1988, 25(7): 612–617. DOI:10.2514/3.45631 |
| [4] | Hu H, Yang Z. An experimental study of the laminar flow separation on a low-Reynolds-number airfoil[J]. Journal of Fluids Engineering, 2008, 130(5): 0511011–1. |
| [5] |
Wu J, Wang J J, Li T. Experimental investigation on low Reynolds number behavior of NACA0012 airfoil[J].
Journal of Experiments in Fluid Mechanics, 2013, 27(6): 32–38.
(in Chinese) 吴鋆, 王晋军, 李天. NACA0012翼型低雷诺数绕流的实验研究[J]. 实验流体力学, 2013, 27(6): 32–38. |
| [6] | Yarusevyc S, Sullivan P E, Kawall J G. On vortex shedding from an airfoil in low Reynolds number flows[J]. J. Fluid Mech, 2009, 632: 245–271. DOI:10.1017/S0022112009007058 |
| [7] | Buchmann N A, Atkinson C, Soria J, et al. Influence of ZNMF jet flow control on the spatio-temporal flow structure over a NACA-0015 airfoil[J]. Experiments in Fluids, 2013, 54(3): 1–14. |
| [8] |
Bai P, Cui E J, Zhou W J, et al. Numerical simulation of laminar separation bubble over 2D airfoil at low Reynolds number[J].
Acta Aerodynamica Sinica, 2006, 24(4): 416–424.
(in Chinese) 白鹏, 崔尔杰, 周伟江, 等. 翼型低雷诺数层流分离泡数值研究[J]. 空气动力学学报, 2006, 24(4): 416–424. |
| [9] | Catalano P, Tognaccini R. RANS analysis of the low-Reynolds number flow around the SD7003 airfoil[J]. Aerospace Science and Technology, 2011, 15(8): 615–626. DOI:10.1016/j.ast.2010.12.006 |
| [10] | Zhang W, Cheng W, Gao W, et al. Geometrical effects on the airfoil flow separation and transition[J]. Computers & Fluids, 2015, 116: 60–73. |
| [11] | Visbal M R, Orkwis P D. Comparative study of implicit and subgrid-scale model large-eddy simulation techniques for low-Reynolds number airfoil applications[J]. International Journal for Numerical Methods in Fluids, 2013, 71(12): 1546–1565. DOI:10.1002/fld.v71.12 |
| [12] | Lee D H, Nonomura T, Oyama A, et al. Comparison of numerical methods evaluating airfoil aerodynamic characteristics at low Reynolds number[J]. Journal of Aircraft, 2015, 52(1): 296–306. DOI:10.2514/1.C032721 |
| [13] | Gross A, Fasel H F. Hybrid turbulence model simulations of partially stalled airfoil flow[J]. AIAA Journal, 2016, 54: 1–15. |
| [14] |
Wang L, Luo Z B, Xia Z X, et al. Numerical simulation of separated flow control on an airfoil using dual synthetic jets[J].
Acta Aerodynamica Sinica, 2012, 30(3): 353–357.
(in Chinese) 王林, 罗振兵, 夏智勋, 等. 合成双射流控制翼型分离流动的数值研究[J]. 空气动力学学报, 2012, 30(3): 353–357. |
| [15] |
Liu P Q, Ma L C, Qu Q L, et al. Numerical investigation of the laminar separation bubble control by blowing/suction on an airfoil at low Reynolds number[J].
Acta Aerodynamica Sinica, 2013, 31(4): 518–524.
(in Chinese) 刘沛清, 马利川, 屈秋林, 等. 低雷诺数下翼型层流分离泡及吹吸气控制数值研究[J]. 空气动力学学报, 2013, 31(4): 518–524. |
| [16] |
Ye J. Large-eddy simulation of blade boundary layer spatio-temporal evolution under unsteady disturbances[D]. Beijing: Beihang University, 2008. (in Chinese) 叶建. 非定常环境中叶片边界层时空演化机制的大涡模拟[D]. 北京: 北京航空航天大学, 2008. |
| [17] |
Ye J. Some improvements on the large-eddy simulation solver for complex compressible flows[R]. Beijing: Beihang University, 2008. (in Chinese) 叶建. 复杂可压缩流动大涡模拟程序的若干改进[R]. 北京: 北京航空航天大学, 2011. |
| [18] | Jones L E, Sandberg R D, Sandham N D. Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence[J]. J. Fluid Mech, 2008, 602: 175–207. |
| [19] |
Wu Z N.
Basic Principles of computational fluid dynamics[M]. Beijing: Science Press, 2001.
(in Chinese) 吴子牛. 计算流体力学基本原理[M]. 北京: 科学出版社, 2001. |



