扑旋翼是一种近年来被提出的微型飞行器[1] (Micro Air Vehicle, MAV) 新布局, 其通过一对翼主动拍动产生升力, 同时产生推力驱动翼进行被动旋转和俯仰运动。扑旋翼相较于传统布局的MAV有高升力、制作简单、可微型化高等优势[2]。与扑翼、旋翼相比, 扑旋翼的运动更为复杂, 其更多需依赖翼的被动运动特性。同时, 这种被动运动与气动特性之间的相互作用是十分值得关注的。
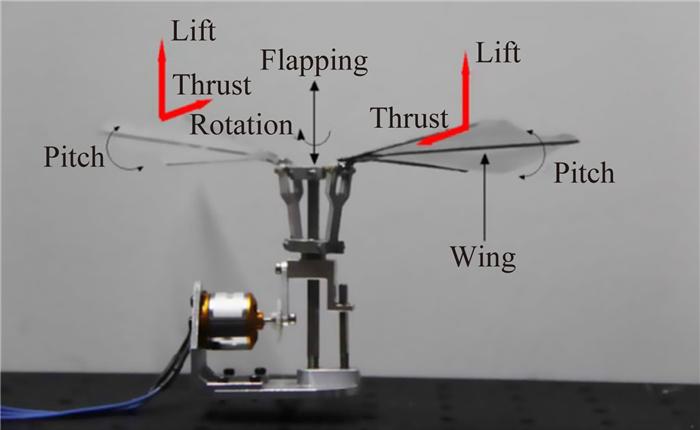
|
| 图 1 典型扑旋翼微型飞行器设计 Fig. 1 A typical flapping rotary wing MAV design |
如何测量和描述扑旋翼MAV在拍动、旋转、俯仰三个方向上的运动[3],以及翼在运动过程中由于力的作用产生的弯扭变形[4]是一个亟待解决的问题。已有的扑旋翼计算流体力学研究中,通常将翼理想化为一个刚性平板,并通过周期性变化的三角函数给出拍动角和俯仰角的运动规律[5];或者忽略翼的被动俯仰运动,仅给定一个初始迎角,而拍动方向和旋转方向上的频率、转速则通过实验数据测得,作为数值计算的输入[6]。这些方法中,某些被动运动部分是人为给定的,这可能与翼的真实运动结果有所不同,有可能会影响到气动力。如果使用数值手段真实求解翼的被动运动,则需用CFD耦合结构动力学进行流动与运动的迭代求解。这是较为复杂的流固耦合问题,计算量大[7]。
一种可行的解决方案是使用CFD与实验测试相结合的手段研究上述问题,即使用数字图像处理的三维重构方法对扑旋翼的运动与变形进行测量和重构,然后将重构结果作为CFD的输入,研究翼的运动影响气动特性的机理。这种方法目前被广泛地应用在昆虫仿生学研究中,Fry等[8]将单相机的摄影测量应用于昆虫运动轨迹的获得,Walker等[9]运用多相机系统的摄影测量来获得食蚜虻和蝗虫的运动。基于背景的匹配方法能够在变形不很大的情况下完成较为准确的识别,在昆虫运动的研究中得到了广泛的应用[10]。
本文采用数值模拟方法研究扑旋翼的被动运动对其对气动特性的影响,其中将摄影测量获得的翼的运动特性作为CFD的输入。首先,介绍翼模型的组成、摄影测量实验平台的布置;其次介绍采用的图像处理方法、网格模型和CFD计算方法;然后,对三维重构得到的运动特性和数值模拟的结果进行对比和分析;最后给出扑旋翼的被动运动特性及其对气动特性的影响机理。
1 模型与方法 1.1 实验平台与扑旋翼模型本研究使用的高速摄影测量平台由以下各部分组成:高速摄像机、机械式扑旋翼运动装置、压力传感器以及光源,实验平台如图 2所示。

|
| 图 2 摄影测量实验平台 Fig. 2 Photogrammetry experiment platform |
为了能够拍摄到各个时刻下翼的运动,并避免出现由于翻折和遮挡引起的标记点不在视场内的问题,我们采用三台高速摄像机,其型号均为FASTCAM UX100 MINI,帧率为2000fps,分辨率为1280×1024。使用40mm定焦镜头,光圈大小根据景深要求设定为8。相机的相对位置如图 2,水平面上每两台相机间夹角为120°,竖直方向低头约60°。机械式扑旋翼运动装置的传动机构由光固化3D打印加工装配。翼的设计模仿自然界的果蝇、蝉等昆虫翼的结构,采用梁加膜形式,如图 3所示,翼梁由碳纤维片组成,截面尺寸为3mm×0.3mm,翼膜由0.07mm的OPP薄膜制作。翼梁和翼膜上布置着共计14个具有明显对比度的标记点。

|
| 图 3 扑旋翼模型 Fig. 3 Flapping rotary wing model |
1.2 运动重构方法 1.2.1 标记点识别
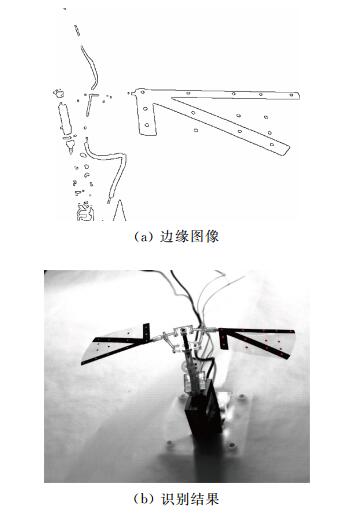
我们使用八邻域扫描方法进行标记点的识别。首先,将高速摄影得到的图像进行二值化,便于后续工作。然后使用Canny法检测图像边缘,进行八邻域的扫描,即对扫描像素点的相邻像素进行分析,逐像素筛选从而确定图像的轮廓,如图 4(a)所示。最后,针对扫描得到的一系列像素,使用一定的尺寸准则来对其构成的形状结构做判断,并去除多点与错点等问题,即获得了识别得到的标记点的轮廓,如图 4(b)中红色点所示。
|
| 图 4 标记点识别过程及结果 Fig. 4 Matching points detection procession and results |
1.2.2 三维重构
首先,使用10cm×10cm的方格标定板对使用的相机系统进行标定,以获取内、外参数 (焦距、主点、扭曲因子、畸变、平移矢量和旋转矩阵等),并确保标定误差在亚像素水平。然后将不同相机获取的标记点坐标序列作为输入,使用相机标定得到的参数,即可将二维坐标重构到三维空间中。
1.3 数值计算方法首先介绍网格模型。本研究中的扑旋翼做非定常运动,并伴随柔性变形,因此在每个物理时间步的开始,网格模型根据翼的位置和拓扑结构的改变而进行更新。首先,对翼进行弦向弯曲、展向扭转的变形,然后以翼的主梁为参考,根据描述翼位置的欧拉角的变化,令翼做转动或平移,并重新计算物面边界的网格。最后,保持外边界网格相对坐标系不动,重构计算网格。重构前,为了快速得到当前时间步的网格,使用Morton提出的改进的超限插值法[12]得到迭代的初始网格,然后使用Hilgenstock提出的求解偏微分方程的方法[13],获得具有良好正交性的网格。本文使用的网格的网格节点数为64×73×79(分别表示沿弦向、周向与展向的节点数),第一层网格间距为0.001c(c为平均气动弦长),边界域大小为30c。网格密度、第一层网格大小、边界域大小这些网格参数都经过了验证,并得到了收敛的结果。翼面附近的网格如图 5所示。

|
| 图 5 翼面处网格 Fig. 5 Grid distribution on the wing surface |
下面介绍求解方法和边界条件。本文的流场基于Rogers和Kwak[14]的拟压缩性法,编写程序来求解三维非定常不可压N-S方程组得到。通过对扑旋翼表面压力和粘性力的积分获取各个方向力与力矩的大小。物面边界满足不穿透壁面和无滑移条件,取翼的运动速度为物面速度,压力梯度通过动量方程计算靠近物面流体法向惯性力得到。远场边界条件方面,入流边界上,速度分量用自由流条件设定,压力由内部推导得到。出流边界上压力定义为与自由流静压相等,速度由内部推导求解。
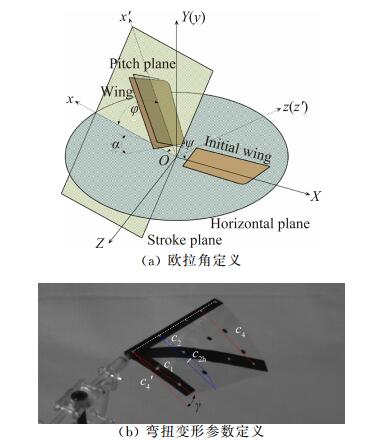
2 实验结果与讨论 2.1 三维重构结果本节从欧拉角变化和弯扭变形规律两个方面介绍三维重构结果中发现的扑旋翼运动和变形规律。首先对三个欧拉角和弯曲度、扭转角进行定义。如图 6(a)所示,拍动角φ指水平面与俯仰平面之间的夹角,旋转角ψ指拍动平面和翼初始位置之间的夹角,俯仰角α指翼实际位置和俯仰平面之间的夹角。弯曲度的定义如图 6(b)所示,沿着展向设置四个位置定义弦向的弯曲并在弦向上布置标记点。图中以c2处为例,弯曲度ε2指弯曲最大位置处的挠度c2h与对应的弦长c2的比值,即ε2=c2h/c2,并且弯曲度ε2与挠度c2h的正负符号相同。扭转角γ指翼根处的弦c1和最靠近翼尖处的弦c4之间的夹角,定义当翼尖后缘位于翼根处后缘下方时,γ为正。
|
| 图 6 运动与变形参数的定义 Fig. 6 Definition of parameters describing motion and deformation |
2.1.1 欧拉角运动规律
基于以上提到的三维重构方法,本节讨论2.0V输入电压,20°初始迎角下扑旋翼的运动学特性。选取了四个拍动周期进行图像处理分析,得到的欧拉角通过拟合和快速傅里叶变换滤波,最终得到一个拍动周期内,欧拉角随无量纲时间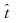
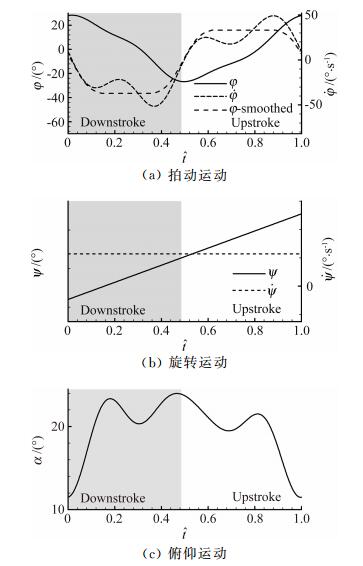
|
| 图 7 翼的运动特点 (输入电压2.0V,初始迎角20°) Fig. 7 Characteristics of wing motion (2.0V voltage input and 20° initial angle of attack) |
扑旋翼的主动运动是拍动,被动运动是俯仰和旋转。首先分析拍动运动 (如图 7(a)),拍动频率是12.3Hz,上拍最大幅度为28°,下拍最大幅度为26°。为更清晰地表示拍动运动,求出拍动角速度随时间的变化趋势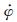
如图 7(b)所示,扑旋翼在旋转方向上匀速转动,达到了平衡状态。如图 7(c)所示,俯仰角在一个拍动周期内会有剧烈的变化。峰值分别出现在下拍过程的中部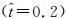
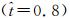
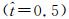
使用与2.1.1节同样的数据处理方法,本节讨论2.0V输入电压,20°初始迎角下扑旋翼的变形特征。
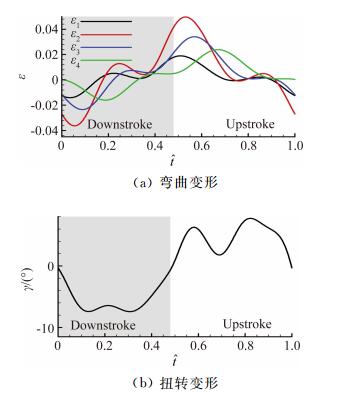
扑旋翼在一个拍动周期内弯曲度随时间变化趋势如图 8(a)所示。以ε1为例,在下拍开始时,弯曲度达到最小值,在下拍进行中略有震荡,产生一个波峰。当下拍结束时,弯曲度达到最大值,上拍过程中的规律与下拍过程类似。弯曲度沿展向逐渐存在相位上的滞后,当到达ε4的位置时,弯曲度的最小值出现在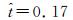
|
| 图 8 翼的变形特点 (输入电压2.0V,初始迎角20°) Fig. 8 Characteristics of wing deformation (2.0V voltage input and 20° initial angle of attack) |
由于扭转沿展向基本呈线性增加的规律,所以仅研究c4位置处的扭转角规律。从图 8(b)所示,在下拍过程中扭转为负,在上拍过程中扭转为正。但在下拍过程中扭转角绝对值始终保持在较大水平,而在上拍过程中只存在一个较大的峰值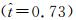
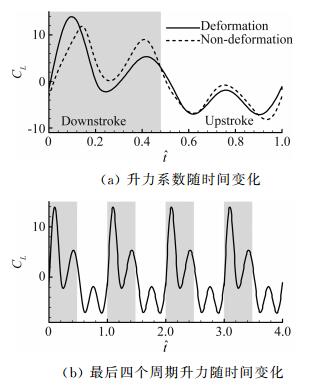
将运动重构的结果作为CFD的输入,得到升力系数随时间的变化规律如图 9(a)所示。其中,虚线为一个不考虑弯曲和扭转的对比算例。本研究中,共计算11个拍动周期,从而保证较好的力周期性。图 9(b)所示为最后四个周期的升力系数随时间变化曲线,可以看到升力符合周期性。下拍过程中,扑旋翼主要产生正升力,期间存在两个峰值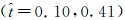
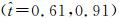
|
| 图 9 升力系数随时间变化规律 Fig. 9 Time course of lift coefficient |
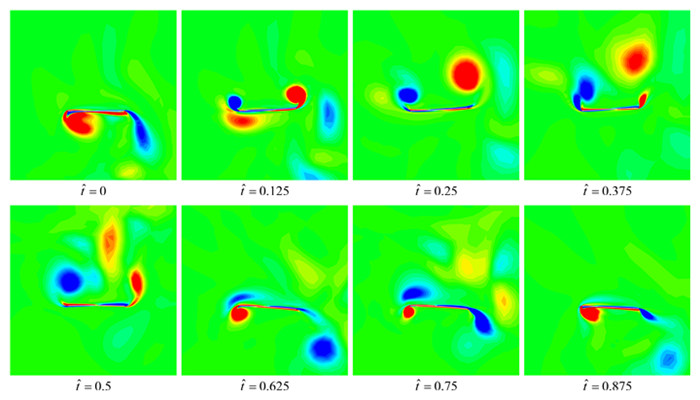
图 10所示为一个拍动周期内翼的二阶矩 (r2) 附近的涡量变化过程。以下拍过程为例,下拍过程开始时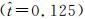
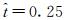
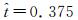
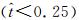
|
| 图 10 一个拍动周期内扑旋翼二阶矩处涡量场 Fig. 10 Vorticity contour plot at wing cross section (r2) during flapping cycle |
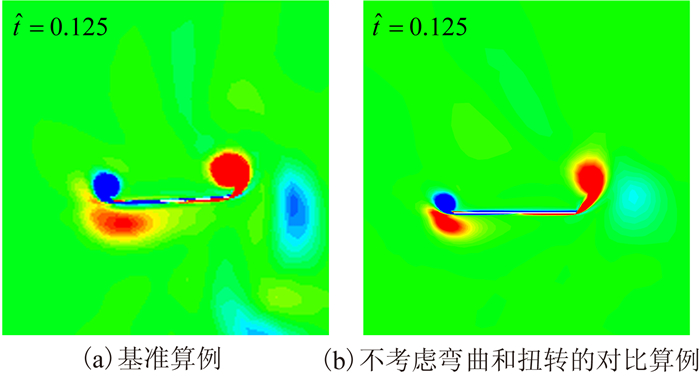
弯曲和扭转对气动特性的影响同样是值得关注的。研究发现,与不考虑弯曲和扭转的对比算例相比,变形翼的平均升力系数更大。并且,下拍过程中,变形翼能够获得更高的峰值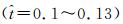
|
图 11 下拍过程中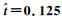 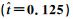 |
3 结论
本文采用实验测量和数值仿真相结合的方法研究扑旋翼的运动规律和气动特性以及相互影响。基于机械式扑旋翼运动模型,使用高速摄影测量获取扑旋翼在真实情况下的运动,并运用边缘识别的数字图像处理的方法,重构了扑旋翼的运动与变形。然后,将运动学结果作为计算流体力学计算的输入,进一步研究了翼的气动特性。主要有如下结论:
1) 基于拍动角φ、旋转角ψ和俯仰角α三个欧拉角的变化,总结出扑旋翼的运动规律。旋转角ψ随时间线性增加,即旋转角速度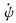
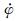
2) 基于沿展向不同位置的弦的弯曲度ε1、ε2、ε3、ε4和扭转角γ,总结出扑旋翼的弯扭变形规律。弯曲度ε1随着翼下拍进行逐渐由最小值变化到最大值,期间出现波动,上拍过程中又再次减小。沿展向上,越接近翼根,弯曲度变化幅值越小,同时在拍动过程中弯曲度发生的震荡越小,ε1曲线最为接近三角波。扭转角γ的变化也较为剧烈,在下拍过程中为负值,上拍过程中为正,在转换过程中迅速变化。
3) 通过CFD结果,总结了翼表面及附近流场随时间发展的规律。在一个拍动过程 (下拍或上拍过程) 中,伴随两次涡的产生、发展和脱落的过程,这表示本研究中流动的非定常性较强。
4) 通过CFD研究弯扭变形对翼表面及附近流动的影响,发现弯曲和扭转能够使翼在运动中产生更强的后缘涡,造成升力峰的提前和峰值的提高。同时,由于弯曲和扭转的方向与涡运动同向,会造成下拍过程中升力系数峰值的提前。
| [1] | Mcmichael J M, Francis C M S, Mcmichael J M, et al. Micro air vehicles-toward a new dimension in flight[J]. Development of the Black Widow Micro Air Vehicle, 1997. |
| [2] | Guo S, Yang D, Kummari K L, et al. A smart material flapping wing micro rotorcraft[R]. Cranfield University, UK. |
| [3] | Zhou C, Wu J, Guo S, et al. Experimental study of the lift generated by a flapping rotary wing applied in a micro air vehicle[C]//Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2013. |
| [4] | Heathcote S, Gursul I. Flexible flapping airfoil propulsion at low Reynolds numbers[J]. AIAA Journal, 2007, 45(5): 1066–1079. DOI:10.2514/1.25431 |
| [5] | Wu J, Wang D, Zhang Y. Aerodynamic analysis of a flapping rotary wing at a low Reynolds number[J]. AIAA Journal, 2015, 53(10): 1–16. |
| [6] | Guo S, Li D, Matteo N, et al. Design, experiment and aerodynamic calculation of a flapping wing rotor micro aerial vehicle. AIAA 2011-1988[R]. Reston: AIAA, 2011. |
| [7] | Chimakurthi S K, Tang J, Palacios R, et al. Computational aeroelasticity framework for analyzing flapping wing micro air vehicles[J]. AIAA Journal, 2009, 47(8): 1865–1878. DOI:10.2514/1.38845 |
| [8] | Fry S N, Sayaman R, Dickinson M H. The aerodynamics of free-flight maneuvers in Drosophila[J]. Science, 2003, 300(5618): 495–498. DOI:10.1126/science.1081944 |
| [9] | Walker S M, Thomas A L R, Taylor G K. Photogrammetric reconstruction of high-resolution surface topographies and deformable wing kinematics of tethered locusts and free-flying hoverflies[J]. Journal of the Royal Society Interface, 2009, 6(33): 351–366. DOI:10.1098/rsif.2008.0245 |
| [10] | Henikoff J, Shapiro L G. Representative patterns for model-based matching[J]. Pattern Recognition, 1993, 26(7): 1087–1098. DOI:10.1016/0031-3203(93)90009-L |
| [11] | Fontaine E I, Zabala F, Dickinson M H, et al. Wing and body motion during flight initiation in Drosophila revealed by automated visual tracking[J]. Journal of Experimental Biology, 2009, 212(9): 1307–1323. DOI:10.1242/jeb.025379 |
| [12] | Morton S A, Melville R B, Visbal M R. Accuracy and coupling issues of aeroelasticnavier-stokes solutions on deforming meshes[J]. Journal of Aircraft, 1998, 35(5): 798–805. DOI:10.2514/2.2372 |
| [13] | Hilgenstock A. A fast method for the elliptic generation of three-dimensional grids with full boundary control[C]//Numerical Grid Generation in Computational Fluid Mechanics'88, 1988: 137-146. |
| [14] | Rogers S E, Kwak D, Kiris C. Steady and unsteady solutions of the incompressible Navier-Stokes equations[J]. AIAA Journal, 1991, 29(4): 603–610. DOI:10.2514/3.10627 |


