湍流角区流动广泛地存在于流体力学与空气动力学工程应用中, 多年来国内外专家学者对其做了大量的研究工作, 取得了很多研究成果, 也发现了一些问题。
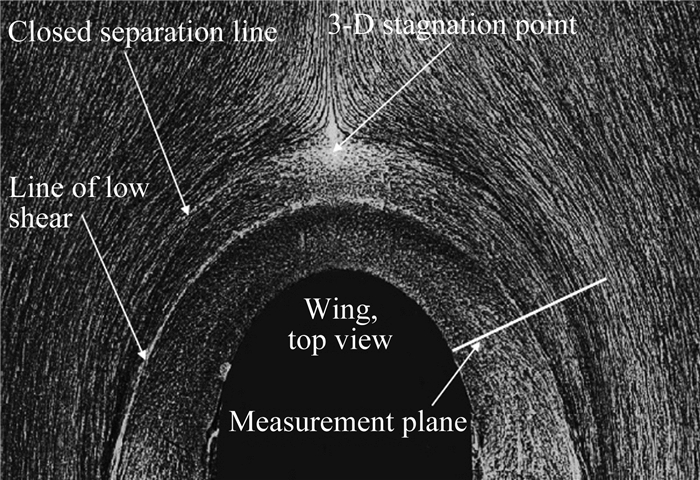
Hunt et al[1]、Baker[2]、Dargahi[3]、Pierce与Shin[4]、Pattenden[5]和Simpson[6]等学者都对角区障碍物周围油流流动进行过研究。图 1为“Rood”翼型前缘的三维分离油流图,可以观测到两条油迹线,Olcmen与Simpson[7-8]将上游的油迹线称为分离线,同时在Devenport与Simpson[9]的研究中,下游的油迹线被称为“低剪切应力线”。Hunt et al[1]和Baker[2]在研究中通过油流图推断出空间四涡流动拓扑结构,表明下游油迹线与流动二次分离和二次涡的关系。Augi和Andreopoulos[10]认为下游油迹线可能由低剪切应力的现象造成,但是并不能确定该线是否与空间流动分离有关。有趣的是,Pierce和Tree[11]研究中却将下游油迹线称为强剪切应力线,并且该线位置与空间最大主涡的涡核中心相对应。不同文献中出现的差异值得注意,需要进一步的研究。
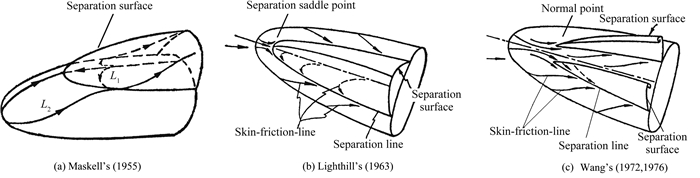
在流体力学与空气动力学工程应用中涉及到的三维分离流动中,广泛应用以下三种分离模式来分析流动,分别是Maskell[12]提出的“极限流线包络线”模式,Lighthill[13]提出的“摩擦力线收拢渐近线”模式,以及Wang[14-15]提出的开式、闭式模式。Maskell[12]用极限流线的方法描述三维分离,认为极限流线汇聚形成的包络线为三维分离线,如图 2(a)。Lighthill[13]引入摩擦力线的概念,表明由鞍点发出的一条摩擦力线S1S2为三维分离线,其临近的摩擦力线都以此渐进收拢,而非相交汇聚,如图 2(b)。王国璋[14-15]提出开式分离模式,认为分离线不从结点或鞍点出发,其两侧的极限流线可以来自与同一附着节点A,如图 2(c)。尽管三种分离模式存在着一些差异,但是它们都反映了三维分离流动中最基本的流动现象:三维分离面及分离涡是由于近壁面的极限流线或摩擦力线从两侧收拢靠近时向上抬起而产生的空间剪切层以及空间涡现象[16-17]。文献[18-22]对于三维分离模式的相关性质进行过讨论。
|
| 图 2 三种不同的三维分离模式 Fig. 2 Three different 3-D separation models |
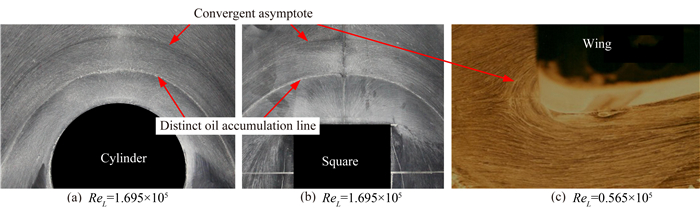
通过对油流实验结果的观察,发现在雷诺数和钝度相对较大的圆柱/平板角区中,三维分离形成的马蹄涡较强,空间马蹄涡系存在着两个主涡和其诱导产生的二次涡[2],表面油流实验得到两条油迹线,上游油迹线表现为渐进收拢线,而下游油迹线并没有明显的渐进收拢特征,表现为清晰明显的油迹堆积,如图 3(a)。在方柱/平板角区中,由于钝度增大,分离较强,这两条油迹线更加明显,如图 3(b)。而在机翼/平板角区中,由于雷诺数和钝度相对较小,空间只存在一个主涡,表面油流只体现出一条符合渐进收拢特征的油迹线,下游并没有第二条油迹堆积线,如图 3(c)。而对于同样的机翼模型,在不同的来流雷诺数条件下,也可能出现不同的油迹线形式,如图 1和图 3(c)所示,即较强分离时为两条特征不同的收拢线,较弱分离时为一条渐进收拢线。油流实验出现的这种差异,与空间旋涡结构和表面摩擦应力的关系密不可分。
|
| 图 3 圆柱、方柱、机翼角区油流实验结果对照 Fig. 3 Comparison of different obstacle juncture surface oil flow patterns |
文献中关于模型钝度和雷诺数等流动参数对于油迹线的影响已经进行过研究,而在本文中,将针对圆柱/平板角区主要探究以下两个问题:
1) 上述两条油迹线为何表现出不同的特性?二者分别对应何种空间流动?
2) 上述两种油迹线各自体现出何种摩擦应力特征?其物理原因为何?
综合采用表面油流流动显示实验以及PIV空间测量实验,并通过CFD数值计算加以补充,旨在对于不同油迹线的性质及其与空间涡的关系作出解释和分析。
1 实验与数值计算设置 1.1 低速风洞实验包括油流实验和PIV实验,这两部分实验均是在北京航空航天大学D-1低速风洞中完成。风洞实验段截面为长轴约1.02m、短轴0.76m的椭圆面,全长1.45m,段内最大风速为50m/s,湍流度约为0.3%。该风洞为开口风洞,可于实验段开口处搭建实验台和实验器材。
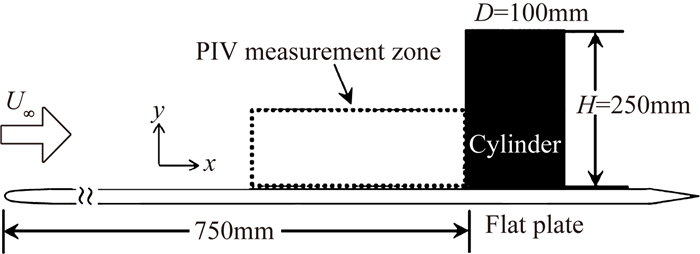
1.2 油流实验油流实验采用圆柱/平板角区,风速为25m/s,ReL=1.695×105。圆柱直径为100mm,高为250mm,由有机玻璃制成。实验装置如图 4所示,圆柱模型放置于1.6m长的平板上,模型前缘距离平板前缘x=750mm。平板前缘截面形状为1/5椭圆形,后缘1/5的斜角,以保证来流在平板前缘不会产生分离。平板上刷亚光黑漆,以保证油流显示的反差与清晰度。

|
| 图 4 实验装置示意图 Fig. 4 Experimental setup in the wind tunnel |
油流实验油液由二氧化钛粉末 (钛白粉)、硅油 (黏度2×10-4 m2/s)、煤油按一定体积比例混合调制而成。配置油液时首先将钛白粉研磨烘烤,通过细网滤掉较大颗粒与硅油混合,并用煤油稀释,通过初步实验确定煤油加入量。
1.3 PIV实验采用北京立方天地公司和镭宝光电公司生产的二维PIV系统,硬件包括型号Vlite-150型激光器 (最大输出能量150mJ)、导光臂、冷却器、同步器及CCD相机。CCD相机采用50mm定焦镜头,空间分辨率为2456×2058。PIV实验设置与油流实验相同,如图 5所示。采用双脉冲激光的形式,相机频率为5Hz,跨帧时间为12μs。
|
| 图 5 角区模型结构示意图 Fig. 5 Sketch of cylinder/plate juncture model |
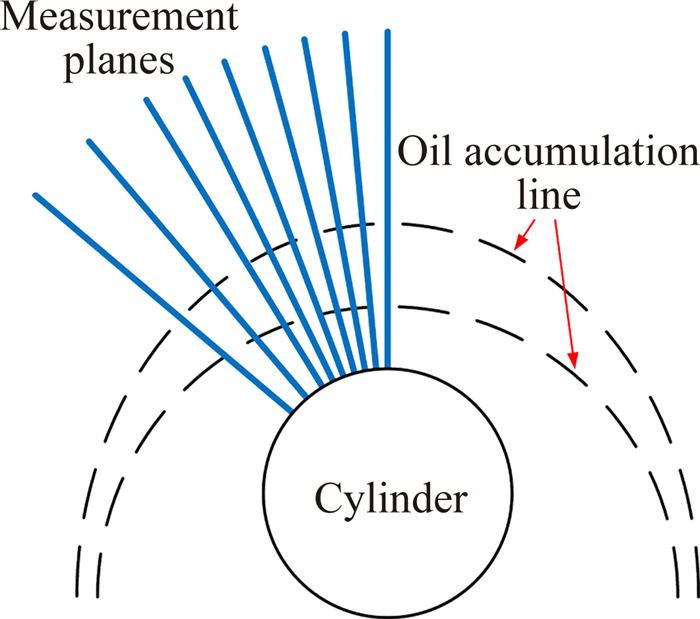
PIV实验重点关注空间对称面中的流动结构,同时加入与对称面成5°、10°、15°、20°、25°、30°、40°、50°夹角的不同截平面的实验进行对照与补充,如图 6所示。
|
| 图 6 PIV实验采样平面示意图 Fig. 6 Measurement planes in PIV experiment |
采用超高浓度烟油,由烟雾发生器直接喷射到流场中得到PIV实验粒子。该粒子属于固体粒子,粒子直径小于1μm,跟随性比较好,并具有较强的散射能力,符合实验要求。烟雾发生器放置于模型下游,喷射出的粒子经过回流到达实验段,满足流场均匀性要求。
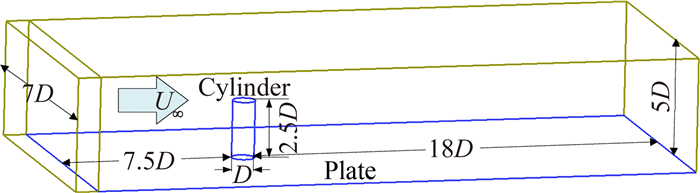
1.4 数值计算设置选取DDES方法对湍流模化,求解过程采用Fractional Step算法,选用Spalart-Allmaras雷诺时均方程。计算域的选取如图 7所示,入口速度为25m/s,来流湍流粘度比为5。出口静压表压为0,回流湍流粘度比为5。计算域的两侧和顶部设置为对称面边界条件,其他壁面满足无滑移条件。
|
| 图 7 数值计算域 Fig. 7 Computational setup for numerical simulations |
2 分析与讨论 2.1 油流实验结果
油流实验作为对照实验,与PIV实验条件一致。参数化油流图片,得到油迹线具体位置数据。
风速25m/s、ReL=1.695×105条件下,通过标定的方法统计不同截平面 (PIV实验采样平面) 与油迹线相交的点到该截平面内圆柱前缘的距离。对称平面内,X1和X2的长度分别代表两条油迹线距离圆柱前缘的距离,如图 8所示。将实验照片放大到实际大小 (以圆柱直径为参考),通过实际测量得到不同截平面内X1和X2的具体数值,结果统计在表 1中。

|
| 图 8 油流实验参数标定示意图 Fig. 8 Setup of oil flow visualization parameterization |
| 角度 | 0° | 5° | 10° | 15° | 20° |
| X1/mm | 50.0 | 49.9 | 49.6 | 49.4 | 49.7 |
| X2/mm | 25.0 | 23.9 | 23.6 | 24.0 | 24.6 |
| 角度 | 25° | 30° | 40° | 50° | 90° |
| X1/mm | 49.9 | 50.1 | 50.2 | 50.3 | 60.2 |
| X2/mm | 24.8 | 24.7 | 24.6 | 25.4 | 39.1 |
2.2 综合分析与讨论
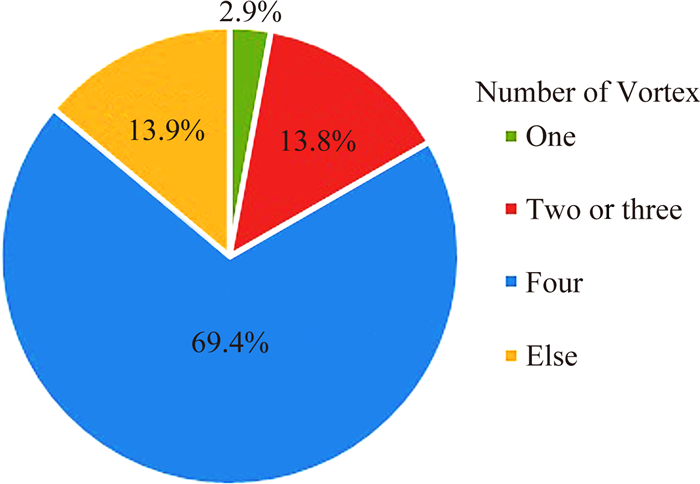
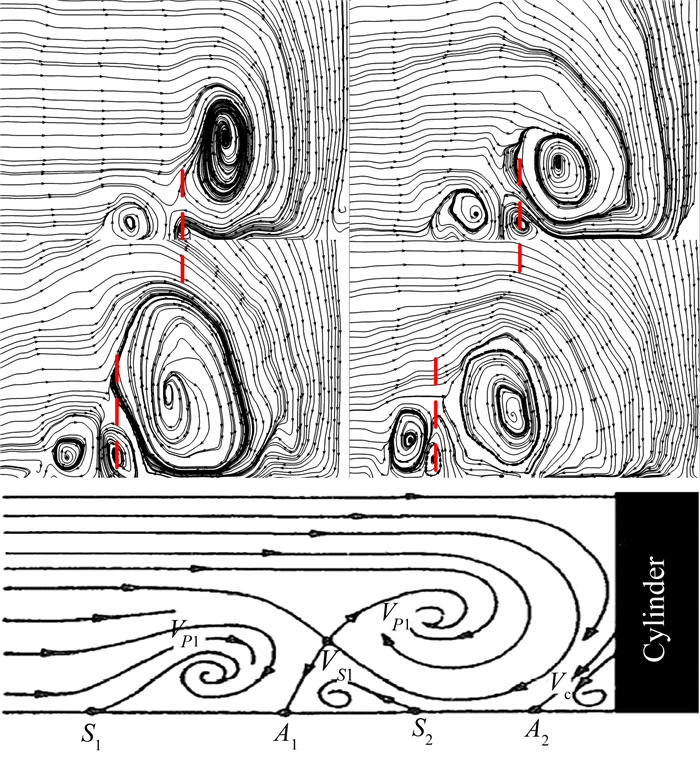
油流结果是空间非定常结构的时均反映。本文实验中空间流动的非定常脉动频率较低,St数约为0.3。由于PIV实验的采样频率相对较低,因此每个工况均采集了大容量的数据样本 (大于5000个)。对于PIV得到的对称平面内的各瞬时流场,通过流线图、涡量云图及λ-2涡识别准则,确定其包含的马蹄涡个数,得到如图 9所示的统计结果,可见四涡结构在一系列的非定常流动中起主导作用。典型的瞬时四涡及其对应的拓扑结构如图 10所示,可见第一主涡 (VP1) 来自于空间鞍点出发的分离面,第二主涡 (VP2) 来自于上游表面的第一条分离线,而二次涡 (VS1) 来自于下游第二条分离线。PIV测量表明四涡结构处于非定常脉动中,所有马蹄涡的位置都处于移动变化中。以二次涡为例,其涡核 (红线标出) 在不同瞬时位置不同,因此无法准确判断二次涡与下游油迹线的关系。
|
| 图 9 PIV得到的各瞬时流场马蹄涡个数的百分比分布 Fig. 9 Percentage distribution of vortex's number in instantaneous structure obtained from PIV experiment |
|
| 图 10 PIV得到的瞬时四涡结构 (上) 及其拓扑图 (下) Fig. 10 Instantaneous structures obtained from PIV experiment and topology of four vortex system |
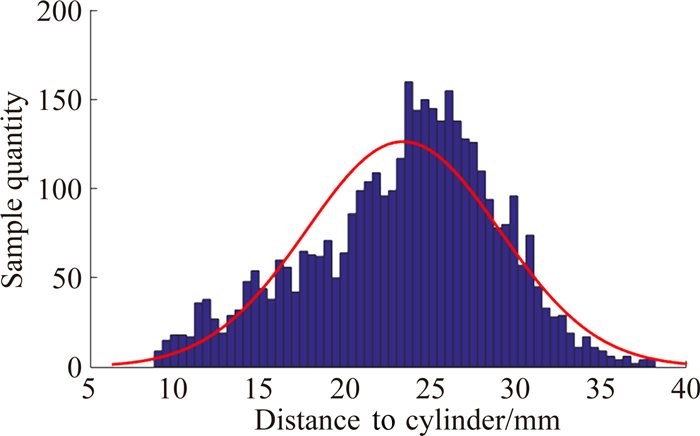
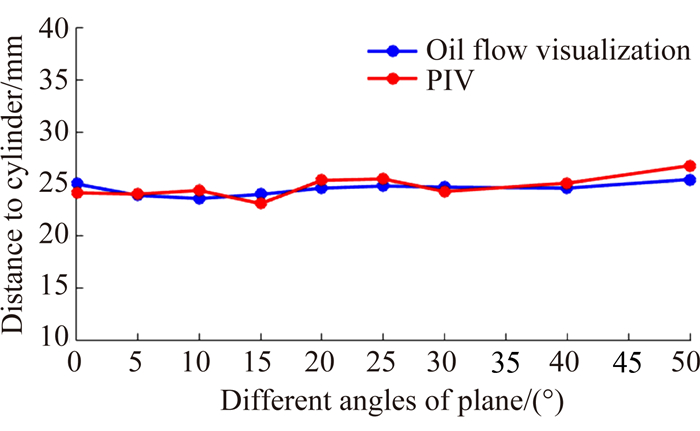
提取对称平面内中各样本二次涡涡核的位置,将所有数据值进行统计,如图 11所示。二次涡涡核主要分布在距离圆柱前缘24mm至28mm的区间内。提取同一截平面内所有样本中二次分离点的位置进行平均,与油流标定数值进行对比,如图 12所示,横坐标表示不同角度的截平面,纵坐标表示二次分离点到圆柱前缘的距离。油流与PIV数值结果相关系数为0.7,体现了较高的相关性,可以认定下游油迹线的产生由二次分离所致。同样,上游油迹线也得到了类似的统计结果。
|
| 图 11 二次涡涡核距离圆柱前缘位置数据样本数量分布 Fig. 11 Sample quantity distribution of distance between secondary vortex core and cylinder lead edge |
|
| 图 12 同截平面二次分离点位置 (PIV) 和下游油线位置 (油流) 对比 Fig. 12 Comparison of secondary separation point and oil accumulation line from different planes |
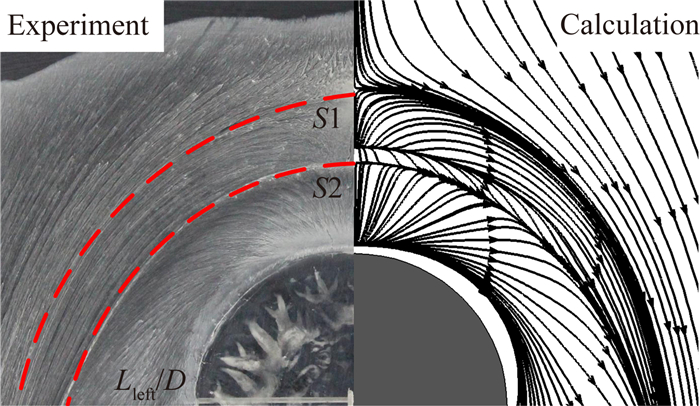
上述油流与PIV实验结果的对比表明了两条油迹线均为三维分离线的性质。然而,同样作为分离线,二者的表现形式却完全不同。如图 13所示的是油流与CFD数值计算结果的对照。可以发现:两条油迹线与CFD计算得到分离线的位置完全相符;上游油迹线符合Lighthill的三维分离模式,其两侧摩擦力线向三维分离线渐进收拢,而下游分离线符合Maskell三维分离模式,其本身为两侧极限流线的包络线;对于两条分离线之间存在的附着线,虽然在油流结果中表现并不明显,但是在CFD结果中十分清晰,这符合已经得到验证的拓扑理论。
|
| 图 13 油流和CFD流动结构对照 Fig. 13 omparison of surface flow pattern obtained from oil flow visualization CFD simulation |
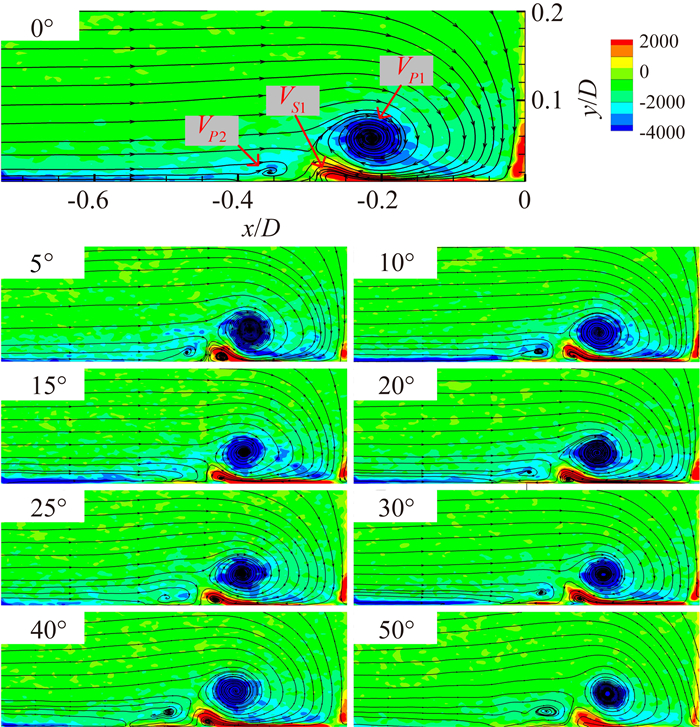
图 14是PIV获得的不同截面中空间涡量的分布,可见各截面空间涡系中第一主涡 (VP1) 与二次涡 (VS1) 的涡强占角区流动的主导作用,二者相反的剪切作用在平板表面形成了二次分离线。在油流实验过程中可以直观观测到:油液流动受到这两个涡的强烈挤压,迅速流向二次分离线,造成油液堆积,使得二次分离线 (下游油迹线) 在油流图中的表现更加明亮。同时,沿着该线的切线方向,油液流速较低,剪切应力势必也会较低。图 15是数值计算得到的表面剪切应力分布及其与表面油流显示的对比。在对应二次分离线或油迹堆积线上,剪切应力较低,其两侧则为剪切应力较高的区域。原因是空间中第一主涡 (VP1) 与二次涡 (VS1) 对平板表面的强烈剪切作用,使得油液沿二次分离线法线方向的分速较高,油迹线两侧的深色区域表明了两侧空间涡对表面油液的冲刷作用。
|
| 图 14 PIV得到的不同截面的涡量云图 Fig. 14 Vorticity contour of flows in different planes obtained from PIV experiment |

|
| 图 15 平板剪切应力云图与油流实验结果对比 Fig. 15 Comparison of surface shear stress contour obtained from CFD and oil flow visualization |
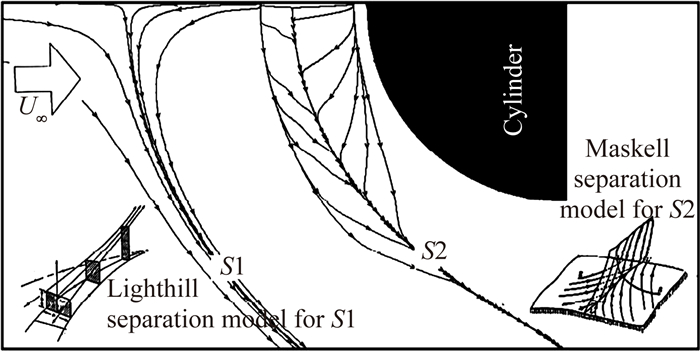
在小钝度机翼角区中,分离情况较弱,只存在一次分离,较弱的空间涡对平板表面的弱剪切无法在分离线两侧的法向形成强剪切应力和油迹的堆积,从而形成符合Lighthill的“渐进收拢”三维分离模式。而在圆柱角区和方柱角区流动中,一次分离和机翼角区分离结构类似,但由于较高的雷诺数和钝度,发生了二次分离,在第一主涡 (VP1) 及二次涡 (VS1) 的强剪切作用下,二次分离线两侧的法向强剪切形成油迹线堆积,较大的近壁法向速度和较小的切向速度使得极限流线在平板表面形成包络线的特点,如图 16所示。
|
| 图 16 圆柱角区三维分离示意图 Fig. 16 Sketch of cylinder/plate juncture 3-D separation models |
3 结论
本文通过油流实验、PIV实验和CFD数值计算,对湍流圆柱角区空间和表面关系进行了讨论。得到以下结论:
1) PIV实验获得的角区空间非定常流动结构的统计结果与油流实验的时均结构是一致的,油流实验中两条油迹线都反映了时均三维分离线,上游分离线对应角区马蹄涡系较弱的第二主涡,下游分离线对应角区的二次分离涡。
2) 一次分离线符合Lighthill的收拢渐近线三维分离模式,二次分离线符合Maskell的包络线三维分离模式。
3) 二次分离线体现出油迹堆积以及低剪切应力特征,因此又可以称为低剪切应力线,其产生的原因是由于空间第一主涡和二次涡的较大涡量在近壁面处的强剪切造成的。
| [1] | Hunt J C R, Abell C J, Peterka J A, et al. Kinematical studies of the flows around free and surface-mounted obstacle: applying topology to flow visualization[J]. Journal of Fluid Mesh, 1978, 86(1): 179–200. DOI:10.1017/S0022112078001068 |
| [2] | Baker C J. The turbulent horseshoe vortex[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1980, 6(1): 9–23. |
| [3] | Dargahi B. The turbulent flow field around a circular cylinder[J]. Experiments in Fluids, 1989, 8(1): 1–12. |
| [4] | Pierce F J, Shin J. The development of a turbulent junction vortex system[J]. Journal of Fluids Engineering, 1992, 112(1): 16–22. |
| [5] | Pattenden R J, Turnock S R, Zhang X. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane[J]. Experiments in Fluids, 2005, 39(1): 10–21. DOI:10.1007/s00348-005-0949-9 |
| [6] | Simpson R L. Junction Flows[J]. Annual Review of Fluid Mechanics, 2001, 33(1): 415–443. DOI:10.1146/annurev.fluid.33.1.415 |
| [7] | Ölçmen S M, Simpson R L. Some features of a turbulent wing-body junction vertical flow[J]. International Journal of Heat and Fluid Flow, 2006, 27(6): 980–993. DOI:10.1016/j.ijheatfluidflow.2006.02.019 |
| [8] | Ölçmen S M, Simpson R L. Experimental transport-rate budgets in complex 3-D turbulent flow near a wing/body junction[J]. International Journal of Heat and Fluid Flow, 2008, 29(4): 874–890. DOI:10.1016/j.ijheatfluidflow.2007.12.004 |
| [9] | Devenport W J, Simpson R L. A time-dependent and time-averaged turbulence structure near the nose of a wing-body junction[J]. Journal of Fluid Mechanics, 1990, 210: 23–55. DOI:10.1017/S0022112090001215 |
| [10] | Agui J H, Andreopoulos J. Experimental investigation of a three-dimensional boundary layer flow in the vicinity of an upright wall mounted cylinder[J]. Journal of Fluids Engineering, 1992, 114(4): 566. DOI:10.1115/1.2910069 |
| [11] | Pierce F J, Tree I K. The mean flow structure on the symmetry plane of a turbulent junction vortex[J]. Journal of Fluids Engineering, 1990, 112(1): 16. DOI:10.1115/1.2909361 |
| [12] | Maskell E C. Flow separation in three dimension[R]. RAE Aero Report, 2565, 1955. |
| [13] | Lighthill M J. Laminar boundary layers[M]. Oxford University Press, 1963: 5-88. |
| [14] | Wang K C. Separation patterns of boundary layer over an inclined body of revolution[J]. AIAA Journal, 1972, 10(8): 1044–1050. DOI:10.2514/3.50292 |
| [15] | Wang K C. Separation of three-dimensional flow[M]. Baltimore: Martin Marietta Labs, 1976. |
| [16] |
Zhang Hanxin, Zhang Shuhai, Tian Hao, et al. Separation on fixed surface for three dimensional compressible unsteady flows[J].
Acta Aerodynamica Sinica, 2012, 30(4): 421–430.
(in Chinese) 张涵信, 张树海, 田浩, 等. 三维可压缩非定常流的壁面分离判据及其分离线附近的流动形态[J]. 空气动力学学报, 2012, 30(4): 421–430. |
| [17] |
Zhang Hanxin, Guo Yijun. Topology of flow patterns on cross section perpendicular to surface of revolutionary body[J].
Acta Aerodynamica Sinica, 2000, 18(1): 1–13.
(in Chinese) 张涵信, 国义军. 垂直于物面的横截面上流态的拓扑[J]. 空气动力学学报, 2000, 18(1): 1–13. |
| [18] | 吕志咏. 三维定常、二维非定常分离模式及准则研究[C]. 力学学术大会, 2000. |
| [19] | 吕志咏, 邓学蓥, 刘谋佶. 定常三维分离准则探讨[J]. 航空学报, 1986, 7(4): 332–339. |
| [20] | Zhang Hua, Younis M Y, Hu Bo, et al. Investigation of attachment saddle point structure of 3-D steady separation in laminar juncture flow using PIV[J]. Journal of Visualization, 2012, 15(3): 241–252. DOI:10.1007/s12650-012-0133-2 |
| [21] | Younis M Y, Zhang Hua, Hu Bo, et al. Topological evolution of laminar juncture flows under different critical parameters[J]. Science China Technological Sciences, 2014, 57(7): 1342–1351. DOI:10.1007/s11431-014-5587-0 |
| [22] | Hu Bo, Zhang Hua, Younis M Y. Experimental investigation on the transition of separation/attachment in steady laminar juncture flows[J]. Experiments in Fluids, 2015, 56(4): 1–9. |