2. 中国计量学院 理学院, 浙江 杭州 310018
2. College of Science, China Jiliang University, Hangzhou 310018, China
射流冲击是一种有效的强化局部传热或传质的方法,由于其直接冲击被冷却或加热的壁面,能够在壁面上形成很薄的边界层,从而使直接受到冲击的区域产生很强的传热传质效果[1]。目前冲击射流已经在许多工程领域中得到了广泛的应用,如纺织品和纸张的干燥、玻璃的回火、钢铁的冷却及加热、飞机机翼除冰、航空发动机涡轮叶片的冷却以及为电子元件的冷却等[1-2]。冲击射流强化传热的研究对这些工业过程的节能运行有着重要意义,因而在过去的数十年中人们对冲击射流开展了广泛的研究。
尽管圆形冲击射流[3]是应用最广、研究最深入的一种射流冲击方式,但是由于狭缝冲击射流可以比圆形冲击射流产生的Nu的分布更均匀[4],采用狭缝冲击射流来进行强化传热的研究越来越得到重视。同时,由于非定常的射流能够破坏流动边界层,显著增加湍流度[5-6],因而非定常的狭缝冲击射流具有强化传热的潜力[7-11]。最常用的非定常射流信号是脉动射流,其强化传热效果在Xu等[7]的单狭缝脉动射流冲击中受到频率、冲击距离等因素的影响,局部传热效果可比稳态提升47%。如今,为了追求更大的传热面积及强化效果,多狭缝射流经常被用于强化传热的数值模拟中[8-14],如改变相邻喷嘴间的相位差[8-10]、利用正弦的振幅比[11]、喷嘴的间距[12]或者喷嘴的数目[13]、应用于冷却带钢的运动生产线的多排狭缝[14]等。脉动射流的占空比[15](射流在一个周期内喷射的时间与整个周期的比) 是非定常射流的一个重要参数,但占空比对多狭缝射流冲击传热影响的研究工作并不多见,特别是对带有相位差的不同占空比下的射流传热性能的认识有待提高。
本文对二维双喷嘴狭缝冲击射流强化传热进行数值仿真,分析了不同占空比的冲击传热性能,在相同的相位差和频率下对比两者的传热性能,这样可以较系统地开展不同占空比对多狭缝射流冲击传热研究工作。
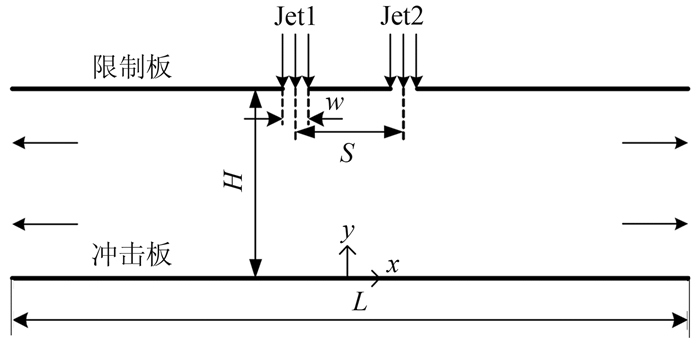
1 模型的建立 1.1 物理描述如图 1所示的半封闭空间内的二维狭缝冲击射流物理模型,双狭缝喷嘴从左至右依次编号为Jet1和Jet2,狭缝喷嘴的宽度都为w,相邻两喷嘴间的间距为S,喷嘴离换热板的高度为H,换热板的长度L为20w,其几何结构和流动参数与文献[10]完全相同:雷诺数Re=5000,喷嘴间距S/w=5,冲击高度H/w=5。射流从各个喷嘴进入,冲击到换热板上,相邻两喷嘴射流间的相位差为θ。图 2给出了脉动射流的流动脉冲剖面图,从中可以直观地获得脉动周期性射流的占空比DC=ton/tc=ton/(ton+toff) 的定义,tc为脉动周期。在数值模拟中,通过UDF编程实现喷嘴射流的不同占空比、相位差和频率来进行计算,得出各因素对传热效果的影响。
|
| 图 1 物理模型示意图 Fig. 1 Schematic diagram of physical model |

|
| 图 2 流动脉冲剖面图 Fig. 2 Profile of the flow pulses |
1.2 控制方程
模拟采用商业软件Fluent6.3,在笛卡尔坐标系中,微分形式的连续方程、动量方程和能量方程可表示为:
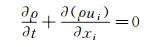
|
(1) |
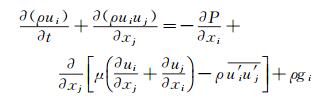
|
(2) |
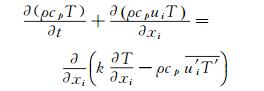
|
(3) |
计算首先对网格数量的无关性进行了验证,模型边界条件设为如下:
1) 喷嘴入口:冲击气体温度设为400K,均匀速度入口;
2) 换热板:固定壁面,无渗透,无滑移,设定初始等温面温度为300K;
3) 出口:采用压力出口;
初始条件为u=v=0,p=p∞,T=T∞。计算过程中湍流模型采用RNG k-ε模型,数值计算采用有限体积法,压力与速度的耦合用SIMPLE方法处理,动量、能量、k和ε方程均采用二阶迎风格式,然后计算收敛的标准是残差小于10-4(除能量为10-6)。
冲击射流雷诺数Re、换热板的对流传热系数h和努塞尔数Nu定义为:
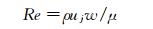
|
(4) |
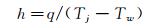
|
(5) |
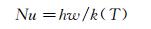
|
(6) |
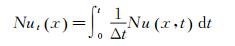
|
(7) |
射流介质设为可压缩流动的空气其物性参数见表 1。
| Properties | Values |
| Density | ρ=3.0753-0.0089T+8.8475×10-6T2 |
| Viscosity | μ=1.4507×10-6+6.6289×10-8T-3.1933×10-11T2 |
| Specific heat | cp=1032.3-0.2104T+4.1274×10-4T2 |
| Thermal conductivity | k=-2.8257×10-4+9.9136×10-5T-3.5751×10-8T2 |
2 结果与分析
相同进口雷诺数下不同占空比[15]的脉动射流会获得不同的冲击传热效果。由于图 1中的模型是对称的,并且计算周期内的相邻两射流也是相同的,而计算后一个周期内的平均Nu也是对称的,所以我们只显示一半的计算结果进行比较。
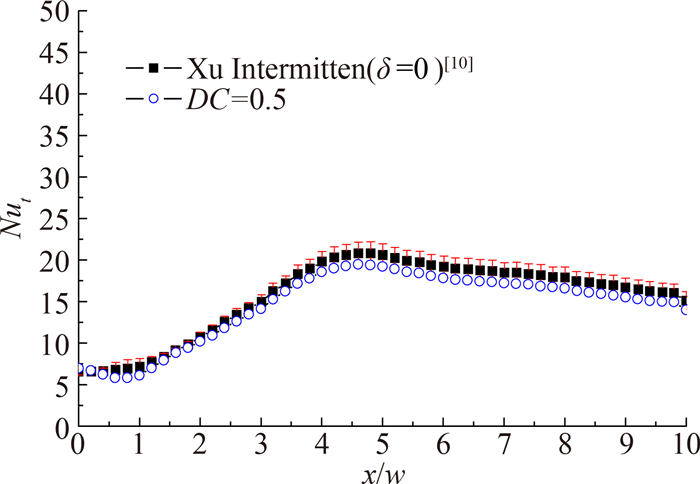
本文分别采用不同的占空比对双狭缝冲击射流进行了计算,并与文献[10]中相应数据进行了对比,相对误差基本上在10%以下,如图 3所示,说明本文建立的数值模型是可靠的。
|
| 图 3 Re=5000,f=50Hz,S/w=5,H/w=5的数值仿真结果对比 Fig. 3 Comparison of the numerical simulation at Re=5000, f=50Hz, S/w=5, H/w=5 |
2.1 不同占空比下的传热分析
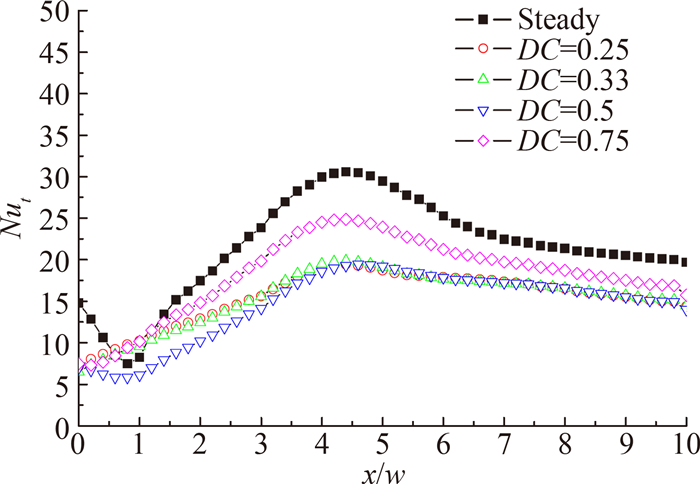
模拟不同占空比DC下的传热性能时,保持脉动射流流速的相对面积不变,即在相同的平均雷诺数下进行。如图 4为射流的频率f=50Hz,占空比DC=0.25、0.33、0.5、0.75的脉动射流和稳态射流,两喷嘴间射流相位差θ为0°时,一个周期内换热板上的平均Nu数分布图。从图中可以看出,不同占空比的脉动射流的传热特性整体上要差于稳态射流,其中脉动射流和稳态射流局部有更强的传热特性,不利于需要加热的器件,这与单喷嘴情况下周期性脉动射流能够强化传热截然不同[7],这是由于周期性脉动射流的不稳定性和更高的湍流、掺混等[7]因素使得两喷嘴间相互作用相互影响的结果,导致两喷嘴射流发生在两喷嘴之间的中心线附近形成涡旋,导致曲线出现先降后升的现象。因此,为了研究两喷嘴的相互作用的影响,针对DC=0.5、0.25时分析不同的相位差θ的效果影响。
|
| 图 4 不同占空比下换热板上的平均Nu数分布 Fig. 4 Average Nu number distribution on heat transfer plate with different duty cycle |
2.2 相位差对传热特性的影响
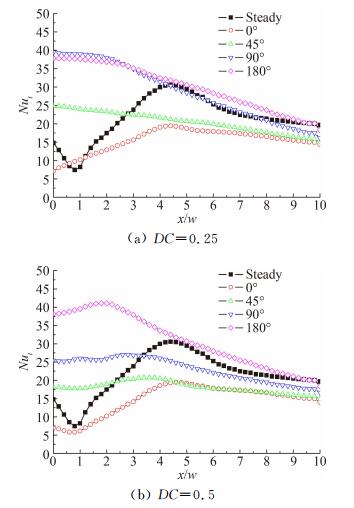
图 5所示射流的频率f=50Hz,占空比分别DC=0.25、0.5的脉动射流和稳态射流,不同相位差θ值时,一个周期内换热板上的平均Nu数分布图。为了便于比较,两种情况的纵坐标保持一致。结果表明,随着相位差θ的增大,两种不同占空比的周期性射流均能获得一定的强化传热效果。这是由于无相位差时进行射流冲击,强烈的射流冲击到壁面转化为沿壁面的横向剪切射流,传热表面受到强烈的相互扰动影响,而相位差使相邻两喷嘴间的速度错开,速度的错开可以减少这种扰动的影响,故在相邻两喷嘴的中心线附近的传热效果相比稳态射流时候明显提高了许多。对比图 5(a)、(b)占空比分别为DC=0.25和DC=0.5的射流冲击相位差比较发现,在DC=0.25条件下,相位差θ值为90°和180°的传热效果强,而在DC=0.5条件下,相位差θ值只有为180°的整体传热效果更好。为了进一步分析相同的相位差而不同占空比的传热效果的差异,有必要分析相位差θ为90°的两种不同占空比下的速度场对传热效果的影响。
|
| 图 5 不同相位差数值下换热板上的平均Nu数分布 Fig. 5 Average Nu number distribution on heat transfer plate with different phase difference |
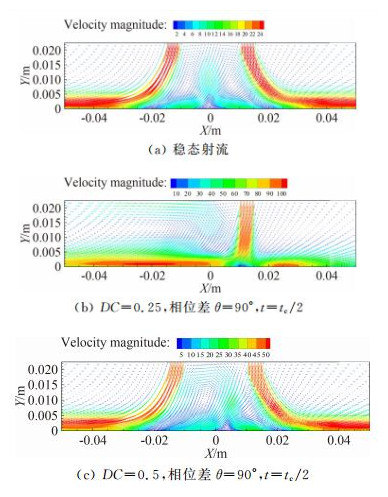
图 6为射流的频率f=50Hz,相位差θ为90°,占空比DC分别为0.25、0.5的脉动射流和稳态射流的速度瞬态矢量图。由图可知,占空比DC为0.25时只有一个喷嘴有射流流动,减少了另一个喷嘴射流的干扰影响,且局部很大的速度抑制了边界层的发展,而占空比为0.5时有两个喷嘴出现射流流动,相邻两个喷嘴之间的射流流动会相互干扰影响,使得射流之间的流动受到影响,边界层得以发展,从而削弱了冲击板的强化传热;同时,错开速度后,由于周期性波动的作用使得射流湍流程度增加,从而达到传热强化的效果。
|
| 图 6 不同占空比下的速度瞬态矢量图 Fig. 6 Instantaneous velocity diagram with different duty cycle |
2.3 频率对传热特性的影响
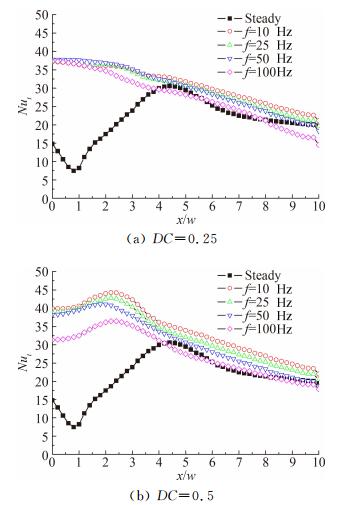
图 7为射流的相位差θ为180°时,不同频率下一个周期内换热板上的平均Nu数分布图。从图中可以看出,频率为0~100Hz之间时,占空比DC为0.5的频率f < 50Hz的平均Nu没有明显的变化,然而随着频率的继续增大,中心线附近的平均Nu明显的降低,但是占空比DC为0.25的传热效果受频率f的影响较小。这是由于有阶跃变化的脉动射流产生强烈震荡和冲击扰动作用,对于单喷嘴非稳态冲击射流,高频变化强化传热[6],而相邻的两喷嘴中不同占空比的高频变化的脉动冲击射流却产生不同的传热效果,频率使传热的强化更加复杂,这其中的机理问题还有待深入研究。
|
| 图 7 不同频率下换热板上的平均Nu数分布 Fig. 7 Average Nu number distribution on heat transfer plate with different frequency |
3 结论
通过对带相位差、不同占空比和频率的非稳态射流在相同的雷诺数下,对比稳态射流的冲击传热模拟研究,本文获得以下结论:
1) 无相位差时,不同占空比的非稳态冲击射流在双狭缝情况下的传热性能低于稳态射流,这是由于非稳态冲击射流在相邻喷嘴之间的相互干扰比稳态的强,使得喷嘴之间的中心线附近的边界层得以发展,从而其总的传热效果被削弱了。
2) 带相位差的周期性狭缝射流冲击传热的效果不仅与占空比有关,而且与相位差数值有关,相位差使相邻两喷嘴间的速度错开,减少了其强烈扰动的影响,故在相邻两喷嘴的中心线附近的传热效果相比稳态射流时候明显提高了许多。相位差为180°时不同占空比下的双狭缝射流在本文的研究范围内平均传热效果最好。相邻两喷嘴间的射流交互作用会影响传热效果的强弱,错开射流速度之间的交互可以强化传热,这对有相位差的多喷嘴提供了一定的研究基础。
3) 频率也是影响冲击传热的一个因素,频率为0~100Hz之间,占空比为0.5的传热存在一个频率阈值,大于这个阈值时的强化传热受到抑制,而占空比为0.25时在这个范围内受频率的影响较小,有阶跃变化的脉动冲击射流产生强烈的震动和复杂的扰动作用,这使得边界层的发展更加复杂化,机理问题还有待深入研究。
| [1] |
Geng T, Li D Q, Zhou H M, et al. Introduction of the study about numerical simulation of heat transfer with impinging jets[J].
Aeronautical Manufacturing Technology, 2006(2): 77–79.
(in Chinese) 耿铁, 李德群, 周华民, 等. 冲击射流传热数值模拟技术研究概述[J]. 航空制造技术, 2006(2): 77–79. |
| [2] | Martin H. Heat and mass transfer between impinging gas jets and solid surfaces[J]. Advances in Heat Transfer, 1977, 13: 1–60. DOI:10.1016/S0065-2717(08)70221-1 |
| [3] | Jambunathan K, Lai E, Moss M A, et al. A review of heat transfer data for single circular jet impingement[J]. International Journal of Heat and Fluid Flow, 1992, 13(2): 106–115. DOI:10.1016/0142-727X(92)90017-4 |
| [4] |
Xu J L, Xu Z, Xiao M, et al. On impinging jet research[J].
Mechanics in Engineering, 1999, 21(6): 8–17.
(in Chinese) 徐惊雷, 徐忠, 肖敏, 等. 冲击射流的研究概述[J]. 力学与实践, 1999, 21(6): 8–17. |
| [5] |
Geng L P, Zhou J W, Li W J, et al. Heat transfer performance and flow field characteristic of a periodical turbulent jet impinging on a plate[J].
Acta Aerodynamica Sinica, 2012, 30(4): 528–532.
(in Chinese) 耿丽萍, 周静伟, 李文军, 等. 周期性湍流射流冲击下的传热与流场特征[J]. 空气动力学学报, 2012, 30(4): 528–532. |
| [6] |
Zhou J W, Yang X X, Geng L P, et al. Experimental investigation on heat transfer augmentation with unsteady impinging jet[J].
Journal of Mechanical Engineering, 2010, 46(6): 144–148.
(in Chinese) 周静伟, 杨兴贤, 耿丽萍, 等. 非稳态冲击射流强化传热试验研究[J]. 机械工程学报, 2010, 46(6): 144–148. |
| [7] | Xu P, Yu B, Qiu S X, et al. Turbulent impinging jet heat transfer enhancement due to intermittent pulsation[J]. International Journal of Thermal Sciences, 2010, 49(7): 1247–1252. DOI:10.1016/j.ijthermalsci.2010.01.020 |
| [8] | Hewakandamby B N. A numerical study of heat transfer performance of oscillatory impinging jets[J]. International Journal of Heat and Mass Transfer, 2009, 52(1-2): 396–406. DOI:10.1016/j.ijheatmasstransfer.2008.07.004 |
| [9] | Mohammadpour J, Zolfagharian M M, Mujumdar A S, et al. Heat transfer under composite arrangement of pulsed and steady turbulent submerged multiple jets impinging on a flat surface[J]. International Journal of Thermal Sciences, 2014, 86: 139–147. DOI:10.1016/j.ijthermalsci.2014.07.004 |
| [10] | Xu P, Qiu S X, Yu M Z, et al. A study on the heat and mass transfer properties of multiple pulsating impinging jets[J]. International Communications in Heat and Mass Transfer, 2012, 39(3): 378–382. DOI:10.1016/j.icheatmasstransfer.2012.01.001 |
| [11] | Jiang Y, Xu P, Mujumdar A S, et al. A numerical study on the convective heat transfer characteristics of pulsed impingement drying[J]. Drying Technology, 2012, 30(10): 1056–1061. DOI:10.1080/07373937.2012.683121 |
| [12] |
Xing G L, Liu H F, Zhou S P. Experimental investigation of convective heat transfer of multiply slot gas impinging jets[J].
Mining and Metallurgy, 2011, 20(1): 38–42.
(in Chinese) 邢改兰, 刘华飞, 周绍萍. 多排狭缝气体冲击射流换热的实验研究[J]. 矿冶, 2011, 20(1): 38–42. |
| [13] | Shariatmadar H, Momeni A, Karimi A, et al. Heat transfer characteristics of laminar slot jet arrays impinging on a constant target surface temperature[J]. Applied Thermal Engineering, 2015, 76: 252–260. DOI:10.1016/j.applthermaleng.2014.10.089 |
| [14] |
Wang Q J, Zhou G, Wen Z, et al. Three dimension numerical simulation of multi-slot gas jet impinging heat transfer[J].
Industrial Furnace, 2013, 35(1): 5–8.
(in Chinese) 王清洁, 周钢, 温治, 等. 多排狭缝型气体射流冲击换热的三维数值模拟[J]. 工业炉, 2013, 35(1): 5–8. |
| [15] | Sailor D J, Rohli D J, Fu Q. Effect of variable duty cycle flow pulsations on heat transfer enhancement for an impinging air jet[J]. International Journal of Heat and Fluid Flow, 1999, 20(6): 574–580. DOI:10.1016/S0142-727X(99)00055-7 |



