动导数风洞试验是采用强迫或自由振荡设备模拟飞行器的刚体运动模态获取动稳定性导数, 是最早研究的单自由度试验技术。在实践中, 动导数风洞试验结果越来越重要, 已成为飞行动力学模态分析最具可靠性的数据来源[1-4]。
在高速动导数试验技术方面,国外已建立了相对成熟的基于强迫振动法或自由振动法的动导数试验体系,试验精度约为10%[5-7]。国内各研究单位也在跨声速风洞及高超声速风洞发展了多套动态试验设备,建立了种类比较齐全的飞行器动态气动特性试验研究平台,适用于飞机、导弹、飞船返回舱等各类飞行器[8-10]。随着航空航天技术的发展,模型外形更趋多样化,传统的高速动导数振动机构已经不能完全满足风洞试验要求,特别是近年大量出现的细长体导弹[11],而目前国内外针对大长细比导弹高速动导数试验相关研究文献却很少。
在高速风洞内实现大长细比导弹动导数试验难度很大,这是因为弹身直径小,模型内腔空间有限,角度天平无足够的安装空间,常规动导数试验机构已不适用;此外,由于导弹类飞行器的滚转阻尼导数量级相对较小,对机构本身的机械阻尼和天平的灵敏度要求较高,精准测量滚转力矩困难[12-13]。
为满足细长体导弹对高速动导数试验提出的型号需求,实现细长体导弹滚转动导数测量,气动院研制了新型滚转动导数振动机构,成功测量了某长细比达18的导弹的滚转动导数,试验精度满足型号要求。
1 滚转动导数试验机构改造常规布局导弹长细比低于10,弹体较粗,对于该类型导弹,国内外各研究单位已进行了大量型号动导数试验,其所采用的传统滚转动导数试验机构的测力和角度天平位于模型腔内,该种形式机构的可靠性已得到了充分认可[5-10]。本文所采用的新型滚转动导数振动机构,结合细长体导弹试验模型和高速动导数试验的特点[11],在原始动导数机构的基础上,进行了3个方面的改造。
1.1 运动转换形式改造运动转换部件用于传动驱动力矩,工作环境复杂,负载大,因此必须有足够的强度和刚度来保证试验机构的可靠运行[12]。
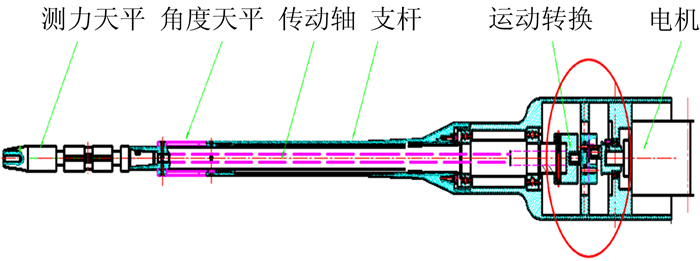
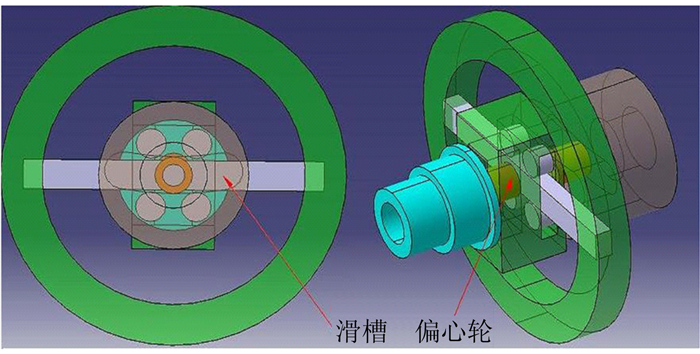
原始滚转动导数机构 (图 1、图 2) 的运动转换原理:驱动电机通过减速器带动偏心轮连续转动,偏心轮在滑块的滑槽里运动,由于滑块通过轴承固定在水平方向的导轨上,滑块只能在水平方向上运动。滑块零件的前端是一个滑轮,传动轴后端是一个弧形滑槽,该滑轮在弧形滑槽里水平运动,带动传动轴往复滚转运动。
|
| 图 1 原始滚转动导数机构 Fig. 1 Original roll oscillation mechanism in roll |
|
| 图 2 改造前运动转换部件 Fig. 2 Key parts of the original mechanism |
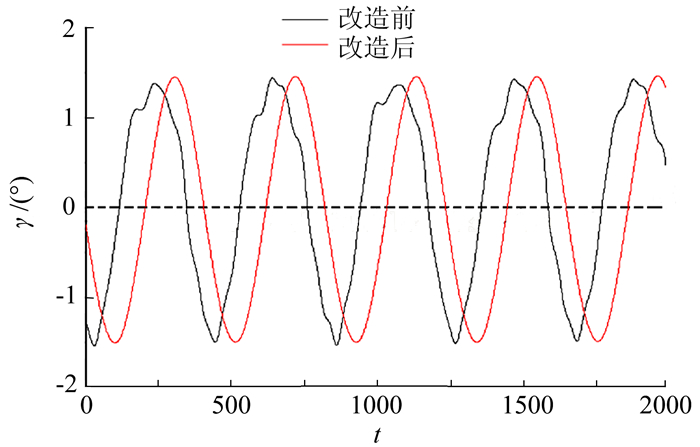
地面调试结果显示,原始机构角度振动曲线对称性及正弦性较差 (图 4)。分析原因认为:偏心轮带动弧形滑槽实现正弦滚转运动的原理是可行的,但受加工水平限制,弧形滑槽的加工精度达不到设计要求。此外,机构自振频率低 (约6Hz),造成滚转方向振动稳定性不足。
|
| 图 4 运动转换部件改造前/后模型滚转角度对比曲线 Fig. 4 Comparision of roll anglefrom the old and new mechanism |
对于常规飞行器风洞试验模型,由于滚转阻尼较大[13-15],振动不稳定带来的误差对试验结果影响有限,然而,对于细长体导弹,由于待测滚转力矩小,滚转阻尼导数量值小,小振动不稳定对试验结果的影响可能是致命的。为了实现小滚转阻尼模型的标准正弦滚转振动,对运动转换部件改造成如下方案 (图 3)。
|
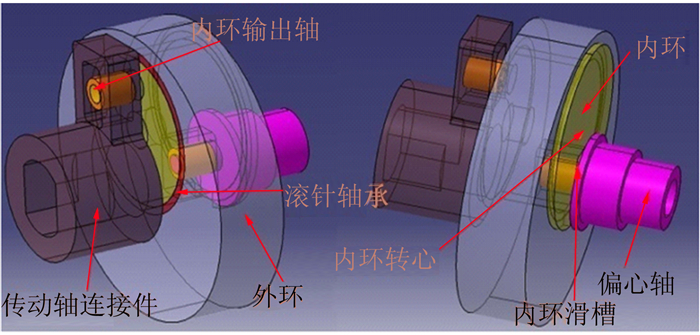
| 图 3 改造后运动转换部件 Fig. 3 Key parts of the modified mechanism |
改造后运动转换原理:内环通过滚针轴承安装在外环上,内环可在外环内自由转动。内环下端为滑槽,上端为输出轴,滑槽和输出轴组成绕内环中心转动的杠杆。电机前端的偏心轴带动内环滑槽绕内环中心左右摆动,内环滑槽左右摆动通过内环杠杆传动转变为输出轴绕内环转心的左右摆动。内环输出轴带动传动轴连接件滑槽左右摆动,进一步转化为传动轴绕外环轴线方向上的滚转往复振动。
改造后的滚转动导数机构加工难度减小,精度易保证,刚度提高,振动平稳,角度天平输出信号稳定、光顺,对称性、正弦性良好 (图 4)。
1.2 角度天平改造本次细长体导弹试验模型弹体细,内腔空间狭小,仅可容纳测力天平,无角度天平的安装空间。针对此问题,新型滚转动导数试验机构将角度天平安装在模型内腔外、支杆末端,其一端与传动轴连接,另一端与支杆连接,一动一静,从而实现滚转角测量 (图 5)。

|
| 图 5 新型滚转动导数振动机构 Fig. 5 New roll oscillation mechanism of dynamic stability derivatives measurement |
该改造在解决角度天平安装空间不足的同时也带来了一些副作用:
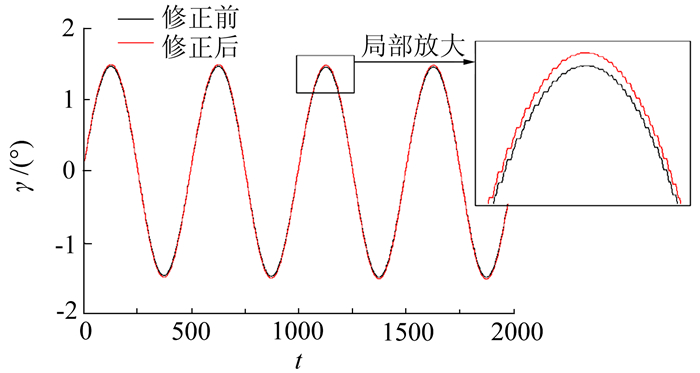
1) 由于模型距离角度天平较远,受传动轴运动时的弹性变形影响,角度天平测量滚转角与模型实际滚转角存在一定的偏差,此偏差可通过地面静加载校准的方式获得支杆弹性变形影响修正公式,对角度测量值进行静态标定修正,从而得到消除。进行静态标定修正主要目的是消除角位移幅值变化对动导数测量的影响。实际进行静态角度修正操作时,为减少修正带来的人为误差,利用同一角度天平,首先在天平末端进行几十个周期测量,提取每个周期角度幅值,以获取模型角位移平均幅值的“真实值A”(天平末端没有支杆弹性变形影响,可认为测量值即为真实值);然后再在支杆末端,以同样方式获得角位移平均幅值“B”;再将二者比值A/B(约为1.018) 带入未修正角度天平公式 (1),即可获得修正后的角度天平公式 (2),修正前后角度曲线对比 (图 6),幅值差量约为1.8%,修正前后对比公式如下:
|
| 图 6 修正前后角度曲线对比 Fig. 6 Comparision of roll angle with and without treatment |

|
(1) |

|
(2) |
其中,X为角度天平测量电压值, V。
2) 传动轴的弹性变形同时也会带来动态影响——角度天平测量的滚转角与模型实际滚转角之间产生的相位差,但该影响属于系统误差,通过有风条件振动得到的阻尼扣除无风条件的机械阻尼即可消除。
1.3 测力天平改造动导数测力天平的设计除了要考虑静态承载能力和测量精度外,还需考虑动态测量精度,这就要求天平响应快、灵敏度高、抗干扰能力强。
滚转力矩作为本项试验最重要的测量值,由于导弹弹翼/舵面展长小,待测滚转力矩量值小,为提高测量精准度,采用特殊的结构形式和有限元优化方法对天平进行了重新设计、加工。主要特点如下:
1) 在满足强度要求的前提下,选取刚度适中的滚转力矩元,最大限度提高滚转方向灵敏度;
2) 为满足纵向力偏大、横向力偏小的特点,天平测量元件选取长宽比较大的截面结构;
3) 采用干扰较小的矩形长边端面测量滚转应力。
2 数据采集与处理本次试验采用PXI动态数据采集处理系统 (图 7) 对动态信号进行采集、处理。采样率为5000Hz,低通滤波截止频率设为20Hz。信号经由放大器、滤波器,由A/D端口进入PXI,生成数字信号。

|
| 图 7 PXI动态采集与处理系统 Fig. 7 PXI dynamic acquisition system |
试验过程中,由于风洞中存在气流脉动、非定常气动力等因素,会对天平测量带来噪声影响,特别是对小阻尼模型试验,由于电压信号弱,传统滤波器消除噪声的方法会使其失真较大。因此,选用合理的数据采集与处理方法是动导数测量试验中的一个关键。本次试验过程中,采用PXI动态数据采集与处理系统可以有效消除噪声及其它信号的干扰,最大限度保留原始电压信号,给出“干净”的力 (力矩) 和角度信号 (图 8),保证导数提取的精准度。

|
| 图 8 PXI处理前后的试验数据对比 Fig. 8 Comparison of experimental data with and without treatment |
数据处理过程中,由VB语言开发的动导数数据处理软件可对原始数据进行分析、判别,对数据坏点进行剔除,并选择合理的数值积分区域,处理结果稳定、可靠。此外,该软件还可对模型的静导数进行提取计算。
3 风洞试验 3.1 试验风洞FL-1风洞为半回流暂冲下吹式亚、跨、超三声速风洞,试验段截面尺寸为0.6m×0.6m。本次试验马赫数范围为0.4~0.95,迎角范围为-6°~10°,侧滑角范围为0°~7°。
3.2 试验模型试验模型为“X”型弹翼/舵面布局导弹模型,缩比为1:12,弹翼/舵面展弦比均小于1,长度为500mm,铝制,等直段直径为28mm,长细比约为18,尾喷口直径为17mm,质量为0.5kg,滚转方向上的转动惯量约为1×10-4kg·m2。
3.3 试验结果图 9给出了地面调试空振试验结果,可以看到,滚转力矩曲线和角度曲线均呈现良好的正弦规律,力矩-角度曲线线性度良好,接近直线,表明该滚转动导数试验机构本身机械阻尼较小 (实测空振阻尼导数约为-1×10-4~-3×10-4),振动特性良好。

|
| 图 9 空振试验结果 Fig. 9 Wind-off experimental results |
由于新机构首次使用,试验初始,利用往期某常规布局导弹试验模型进行了机构可靠性验证试验,试验马赫数为0.6,试验结果见图 10。可以看出,除12°迎角外,滚转阻尼导数变化规律一致,且量值相当,证明了新试验机构可靠,试验数据可信,可以承接型号试验。

|
| 图 10 机构可靠性验证试验结果,f=12 Fig. 10 Experimental results of mechanism reliability verification, f=12 |
图 11所示为本期重复性试验结果,可以看出在迎角-4°~4°范围内,滚转阻尼导数重复性误差约15%,这是由于此次试验模型的滚转力矩非常小,动态滚转力矩也是小量,从图 9中可以看出动态滚转力矩振幅约为0.03Nm,其幅值仅为天平设计载荷 (1Nm) 的3%,在如此苛刻的条件下,取得的尚可接受的重复性结果间接证明了振动机构稳定、可靠以及天平的优异性能。

|
| 图 11 Ma=0.8,f=12,重复性试验结果 Fig. 11 Ma=0.8, f=12, repeated experimental curve |
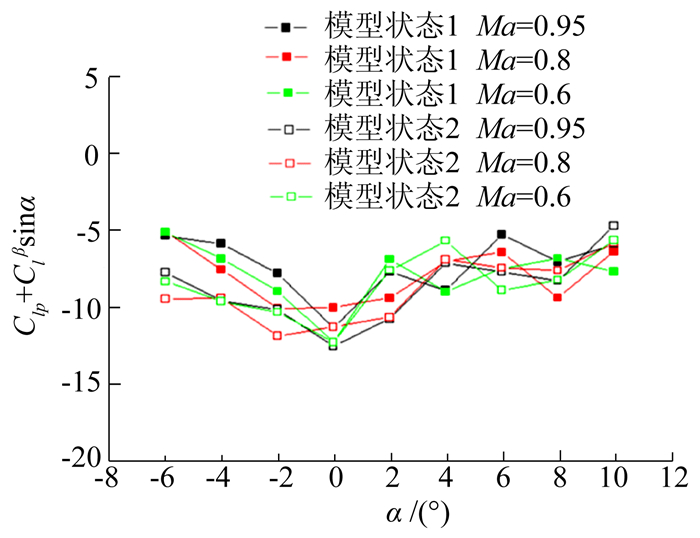
图 12所示为不同模型状态/不同马赫数的试验结果,模型状态1为巡航构型 (无助推器),模型状态2为助推构型 (有助推器)。可以看出在试验工况下,动导数均为负值,没有出现导数变号情况。这是由于弹翼展弦比小,后掠角大,在试验迎角范围内流场没有出现大的分离,结合图 13中的静态力结果分析,在试验迎角范围内,模型法向力基本是随迎角线性增加,表明机翼上的流动以附着流为主,而滚转阻尼主要来源于左右弹翼当地迎角不同而产生的升力不同所带来的滚转力矩。所以在试验迎角范围内,滚转阻尼随迎角变化不大。
|
| 图 12 f=12,不同模型状态/不同马赫数试验结果 Fig. 12 Experimental results of different states and Math numbers, f=12 |
|
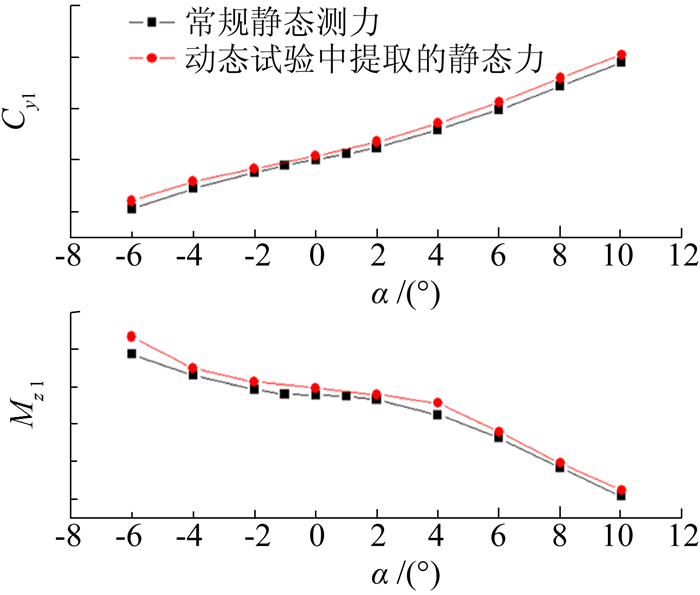
| 图 13 试验中提取出的静态力与常规测力试验结果对比 Fig. 13 Comparison of static force from dynamic test and static test |
图 13所示为本次试验中提取出的静态力与常规测力试验得到的静态力结果对比,动态试验中采用的模型比例为1:12,而静态测力试验中模型比例为1:5。动导数试验中静态数据的提取方法:将空振过程中和吹风过程中每个名义迎角下的天平读数进行平均处理,并对应相减,再计算得到静态载荷。可以看出,不同模型比例下的两种试验结果取得了良好的一致性,一方面证明了动导数测量设备的可靠性,另一方面也展示了动导数试验对静态试验结果的包容性:随着动导数试验技术的进一部发展,动导数试验中提取的静态力与常规测力结果吻合度达到了一定的高度,试验精度的进一步提升,在一定的程度范围内,可以兼容常规测力试验,降低试验成本。
4 结论本次试验取得了良好的试验结果,试验重复性精度较高,得到的数据符合气动规律。证明了新型滚转动导数测量机构稳定、可靠,成功地解决了细长体导弹在滚转动导数试验中遇到的问题。
经过本次试验技术研究,可以得到以下结论:
1) 动导数试验中,尤其是对导数量值小的试验,机构振动稳定性直接决定着试验的成败;
2) 在天平支杆末端安装角度天平,实时测量模型滚转角的方式是可行的,可以解决角度天平无法在细长体导弹模型狭小的内腔安装的问题;
3) 改造后滚转测力天平具有良好的抗干扰特性,能够在天平量程小范围内精确测量, 可测得仅为3%天平设计载荷的动态滚转力矩。
| [1] |
Li Zhoufu.
Wind tunel special tests technique[M]. Beijing: Aviation Industry Press, 2010: 209-220.
(in Chinese) 李周复. 风洞特种试验技术[M]. 北京: 航空工业出版社, 2010: 209-220. |
| [2] |
Fan Jiechuan.
Handbook of wind tunnel test[M]. Beijing: Aviation Industry Press, 2001.
(in Chinese) 范洁川. 风洞试验手册[M]. 北京: 航空工业出版社, 2001. |
| [3] | Owens D B, Brandon J M, Croom M A, et al. Overview of dynamic test techniques for flight dynamics research at NASA LaRC[C]//25th AIAA Aerodynamic Measurement Technology, and Grand Testing Conference, 2006. |
| [4] | Jansson T, Torngren L. New Dynamic testing techniques and related results at FFA. ADP005024[R]. Lindin: AGARD 1985, 20. |
| [5] | Tomek D M. The new generation of high-speed dynamic stability wind tunnel testing. AIAA 2006-3148[R]. Reston: AIAA, 2006. |
| [6] | Cyram B. Sting interference effects on the static, dynamic, and base pressure measurements of the standard dynamic model aircraft at mach numbers 0.3 through 1.3. AEDC-TR-81-3[R]. Tennessee: AEDC, 1981. |
| [7] | Coulter S M, Marquart E J. Cross and cross-coupling derivative measurements on the standard dynamic at AEDC. AIAA-82-0596[R]. Reston: AIAA, 1982. |
| [8] |
Zhao Zhongliang, Ren Bin, Huang Xuhui, et al. Investigation on model dynamic stability derivatives test techniques in trans-supers-hypersonic wind tunnels[J].
Acta Aeronautica et Astronautica Sinica, 2000, 21(1): 52–56.
(in Chinese) 赵忠良, 任斌, 黄叙辉, 等. 跨超、高超声速风洞模型动导数试验技术研究[J]. 航空学报, 2000, 21(1): 52–56. |
| [9] |
Bai Kui, Feng Mingxi, Fu Guangming. Experimental technique for rolling aerodynamic of slight asymmetric re-entry body[J].
Experiments and Measurements in in Fluid Mechanics, 2002, 16(3): 63–72.
(in Chinese) 白葵, 冯明溪, 付光明. 小不对称再入体滚转气动力测量技术[J]. 流体力学实验与测量, 2002, 16(3): 63–72. |
| [10] |
Gong Weibin. Experimental techniques of reentry booy dynamic derivatives[J].
Experiments and Measurements in in Fluid Mechanics, 1997, 11(1): 30–34.
(in Chinese) 龚卫斌. 再入体动导数试验技术[J]. 流体力学实验与测量, 1997, 11(1): 30–34. |
| [11] |
Pan Jinzhu, Zhang Jie, Cai Yi. Investigation on the high-speed wind tunnel dynamic test techniques[J].
Acta Aerodynamica Sinica, 2016, 34(5): 606–610.
(in Chinese) 潘金柱, 张杰, 才义. 高速风洞动导数试验技术研究[J]. 空气动力学学报, 2016, 34(5): 606–610. |
| [12] |
Wang Xinke, Zhang Rui, Ju Bo, et al. Wind tunnel dynamic derivative pitching vibration test device design[J].
Ordnance Industry Automation, 2014, 33(8): 72–74.
(in Chinese) 王新科, 张锐, 鞠波, 等. 风洞动导数俯仰振动试验装置的设计[J]. 兵工自动化, 2014, 33(8): 72–74. DOI:10.7690/bgzdh.2014.08.020 |
| [13] |
Liang Bin, Zhao junbo, Fu Zengliang, et al. Investigation of roll damping derivative of aircraft by wind tunnel tests[J].
Journal of Experiments in Fluid Mechanics, 2016, 30(5): 61–66.
(in Chinese) 梁斌, 赵俊波, 付增良, 等. 飞行器滚转阻尼导数测量试验技术研究[J]. 实验流体力学, 2016, 30(5): 61–66. |
| [14] | Pilmoor M. Development of a dynamic wind tunnel model for demonstration of flow control maneuver effectors. AIAA 2006-3507[R]. Reston: AIAA, 2006. |
| [15] |
Sun Tao, Gao Zhenghong, Huang Jiangtao. Identify of aircraft dynamic derivatives based on CFD technology and analysis of reduce frequency[J].
Flight Dynamics, 2011, 29(4): 15–17.
(in Chinese) 孙涛, 高正红, 黄江涛. 基于CFD的动导数计算与减缩频率影响分析[J]. 飞行力学, 2011, 29(4): 15–17. |



