2. 布朗大学 工程学院, 美国 普罗文登 02906
2. School of Engineering, Brown University, Providence 02906, The United States of America
20世纪90年代后期, 受NASA与美国空军资助的一些气动弹性专家, 如Dowell[1]与Silva[2]等, 提出了基于CFD数值模型构造流场降阶模型 (Reduced-OrderModel, ROM) 的理论, 有效地降低了计算时间并保证了计算精度。ROM是一种在保证计算精度与降低计算时间的条件下,将流场全阶模型通过降阶的模型进行替代的方法。
目前流固耦合系统中非定常流场的ROM主要有两类[3]:基于本征正交分解[4]的ROM与基于系统辨识方法的ROM (Volterra级数[5]、带外输入的自回归[6]模型、递归结构的代理模型[7]、神经网络模型[8])。此外还有一种非线性气动力的谐波平衡方法[9](Harmonic Balance, HB) 被用于气动力求解。其中,因为系统辨识方法中的神经网络模型具有主动学习、容错性强和具有强大的预测非线性系统的能力等优势,所以一批学者针对神经网络建模进行了深入的研究。例如Lindhorst[10]通过使用径向基函数 (Radial Basis Function, RBF) 神经网络并结合POD与Markov链与对两自由度的气动弹性系统建模,但并不能预测大幅迎角升力系数以及力矩系数;Ghoreyshi[11]等基于RBF神经网络,运用Euler与N-S方程的气动力响应同时进行模型训练,提高了预测精度,但只是针对低速情况;史志伟[12]等基于两步回归参数辨识法,建立了两步线性回归的状态空间模型,并预测了某飞机三角翼在俯仰与偏航运动时的气动参数。但该模型有其自身结构的局限性,不能准确地预测更为复杂的运动情况,且模型精度有待提高;Zhang[13]等与王博斌[14]等通过引入RBF神经网络的输出反馈,可以有效模拟非定常流场中的迟滞现象,构建的基于递归向基函数 (Recursive Radial Basis Function, RRBF) 神经网络的气动力模型,分别预测了升力系数、力矩系数以及极限环颤振响应。但从文献[13]的分叉点预测结果可见,模型对不同振幅的泛化能力仍然不理想。综上,神经网络气动力建模存在的问题总结起来可以归结于两点:计算精度不足与模型泛化能力不足。
前人也对提高神经网络建模精度以及模型泛化能力做出了一系列研究。针对模型精度的提高,Du[15]等提出了在同一染色体中编码结点、输入和中心与宽度,用遗传算法进行全局寻优,但寻优过程复杂,不容易实现;Kurkova[16]等提出通过核方法来提高RBF模型的泛化能力,但是高阶Volterra核难于计算;寇家庆等[17]提出用ARX模型预测线性部分输出、用神经网络模型预测非线性部分输出来增强模型来增强模型的泛化能力,但是宽度的选取通过试错法,效率较低。对于RBF神经网络模型预测气动力最主要的影响因素之一就是神经元中心宽度,所以针对每个神经元找到其所对应的最优宽度是RBF神经网络模型精度与泛化能力的关键。
为解决宽度的选择问题,以保证更好的泛化能力,本文发展了一种使用差分进化算法优化与引入小幅高频验证信号计算非线性气动力的RRBF模型,采用固定的神经元位置,针对每一个神经元的宽度用差分进化算法进行寻优,并且引入验证信号作为优化目标,在避免过拟合的情况下增强模型泛化能力。
1 气动力建模本文发展了带验证信号的差分进化算法优化递归径向基函数神经网络 (Differential Evolution-Recursive Radial Basis Function Neural Network, DE-RRBFNN),此模型是一种基于CFD的神经网络气动力模型,属于基于系统辨识的降阶模型。
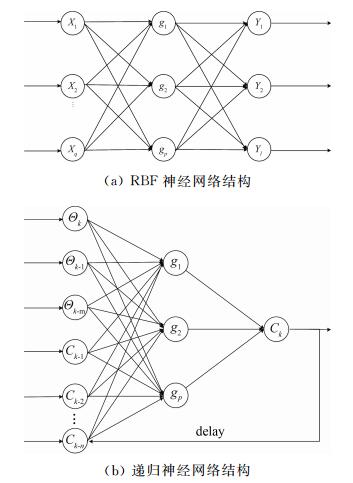
1.1 递归径向基函数神经网络RRBF神经网络是将静态RBF神经网络引入动态延迟而来,前者继承了RBF神经网络的结构。如图 1(a),RBF神经网络可实现映射X→Y, X∈Rq, Y∈Rl, l>1,(X是一个q维的输入向量,Y是对目标输出函数的逼近,为l维向量)。Y表达式为:
|
| 图 1 RBF与递归RBF神经网络模型结构 Fig. 1 Framework of RBF and RRBF neural network |
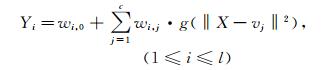
|
(1) |
该神经网络模型有c个隐含层神经元,wi, 0为神经网络偏移,wi, j为第i个输出对第j个隐含层神经元的权重,g为高斯基函数。
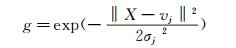
|
(2) |
在计算迟滞效应很强的非定常气动力时,RBF神经网络由于不带反馈,便出现了自身的局限性。RBF神经网络从本质上来讲是一个准定常模型,所以计算定常流场时的结果精度较高。但是对于计算非定常效应十分明显的流场时,模型的结果将具有很大误差。若提高模型的非定常流场计算能力,还需改变其固有属性,即通过引入输出反馈体现非定常效应。
此模型依托的RRBF神经网络是一种三层递归式网络,分别为输入层、隐含层和输出层。输入层由神经元结点组成,如图 1(b)。作为外输入的每一个神经元结点通过非线性函数映射,映射至隐含层的每一个神经元中,并构成隐含层。最后,隐含层通过线性映射 (与各个神经元权重相乘) 到输出层并在输出层中反馈部分信号至输入层[13]。
RRBF模型是一种有效的改变RBF神经网络模型准定常属性的新模型。该模型在输入端引入了部分输出层的输出,即升力系数和力矩系数。计算升力时,模型的输入如下式:
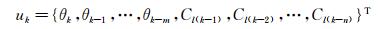
|
(3) |
计算力矩系数时,模型的输入如下式:
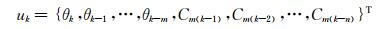
|
(4) |
在计算k时刻结果时引入了k-1至k-n时刻的结果,也就是k时刻结果是基于k-1至k-n时刻结果得来的 (n为延迟阶数,也就是引入输出层结果至输入层的个数)。这样就增强了所计算结果与之前结果的关联性,也就是增强了预测非定常流动之间的迟滞效应的能力,所以RRBF模型更加适合计算非定常气动力。
RRBF模型工作流程如下:如图 1(b),通过CFD求解器计算机翼俯仰运动下的升力系数、力矩系数。随后,将俯仰位移作为RRBF模型输入,经过高斯基函数映射至隐含层,然后再经线性映射至输出层,得出升力系数与力矩系数。之后再将升力系数与力矩系数带回至输入层,与下一时刻位移输入一同组成该时刻的输入。
1.2 宽度的影响宽度是高斯基函数作用范围的表征。由式 (2) 可以看出,宽度的不同可以使隐含层输出有所不同。相同的输入下,宽度越大,隐含层输出越小。同时宽度的调整也关乎最后模型的准确性,不同中心宽度的模型具有不同的精度,最优的参数也能使模型获得最优精度。寇家庆[18]等通过研究宽度对模型精度的影响,发现对RRBF神经网络气动力模型采用不同宽度可能跟大程度影响模型的泛化能力。以往的模型设定的是神经元之间同一宽度。但是实际上,由于非线性输入的存在,使得神经元之间的距离不一致。这样的不准确的宽度设置导致了很大的预测误差。所以为了提升精度,该模型使用差分进化算法对隐含层神经元的宽度进行调整,以增强该模型的泛化能力。
1.3 差分进化算法差分进化 (Differential Evolution, DE) 算法实际上是一种并行导向性搜索方法,可以通过NP个向量xi, G, i=1, 2, …, NP搜索多代进行寻优[19]。该算法简单易用、稳健性好、有强大的全局搜索能力、待定参数少、不易陷入局部最优、收敛速度快。上述优点使得差分进化算法十分适合搜索最优宽度矩阵。
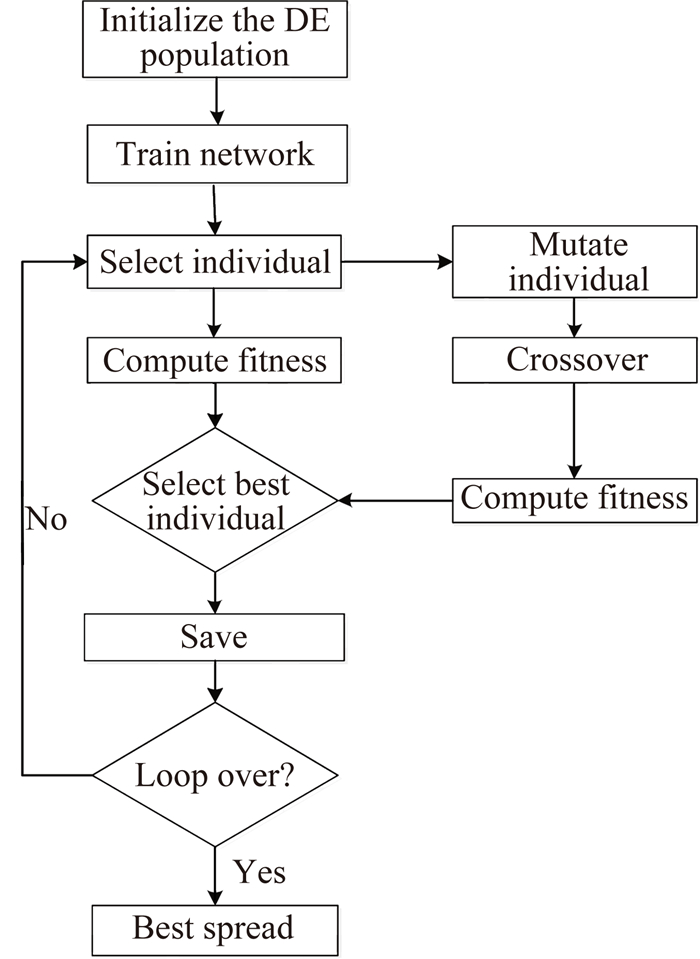
差分进化算法的一次计算过程如图 2所示。此算法是一个迭代过程。先由计算机对每个神经元生成一个一定范围内的随机数, 也就是1×P维的宽度矩阵。然后通过一定规则变异、交叉并产生新个体。再比较新个体与未变化之前的个体的适应度函数 (该宽度下,模型预测的升力与CFD计算得到升力系数之差的2-范数),选择出优秀个体。之后再次变异,交叉种群中的个体生成新个体直至种群所有个体都经历过以上运算,最后选择出优势个体,保存并重复以上步骤G次。此算法中的交叉、变异是模仿生物DNA在复制中的变异与交叉过程。变异是保证初始向量中的个体能够变异,而交叉则是保证一段序列能够变异。变异与交叉实为寻找全局最优解的保证。
|
| 图 2 差分进化算法模型 Fig. 2 Differential evolution algorithm model |
变异步骤:随机生成三个小于宽度矩阵阶数的整数r1、r2、r3。第i+1代跨度矩阵hi+1, n由如下规则算法生成:
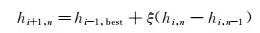
|
(5) |
其中,hi-1, best为i-1代最优宽度矩阵,ξ为概率密度符合高斯分布的随机数,hi, n与hi, n-1分别为第i代种群中第n和第n-1个宽度矩阵。
交叉步骤:对于每一个新生成宽度矩阵中的宽度,命令计算机随机生成一个 (0, 1) 的随机数, 若该随机数大于交叉因子CR,则原宽度矩阵保持不变;若该随机数小于CR,则宽度交叉。
在此优化模型中,共4个参数需要设置,分别是变异因子F,交叉因子CR,遗传代数G与种群数量Size。
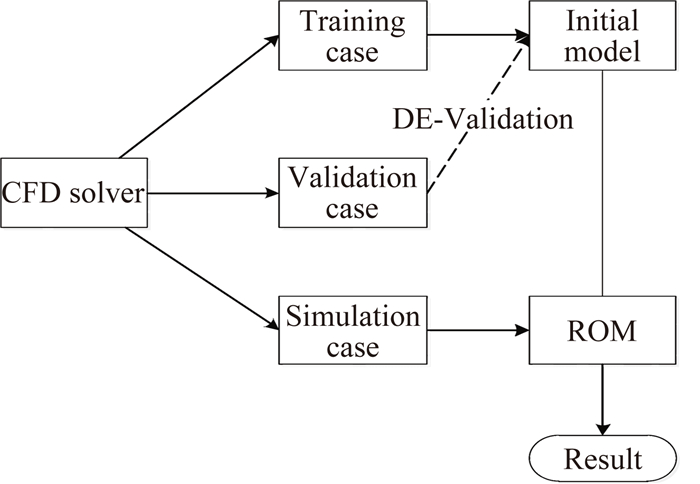
1.4 增强模型泛化能力前人已经针对增加神经网络泛化能力的工作做出了一系列研究,如Zhao[20]等引入k均值聚类与混合学习算法至神经网络;Lueng[21]引入梯度下降法去消除亚最优结果,从而优化宽度。Ni[22]等通过在神经网络中引入验证算例来增强模型泛化能力。本模型选用引入带验证算例的递归神经网络模型来增强模型的泛化能力:训练信号完成模型训练后,验证信号的预测误差作为差分进化算法的适应度函数,以寻找最优的模型宽度。主要过程如图 3。
|
| 图 3 差分进化算法优化递归径向基函数神经网络的建模过程 Fig. 3 Modeling process of the recursive radial basis function neural network optimized by differential evolution algorithm |
在图 3中值得注意的是三组样本含义,如下:
1) 训练样本:用于RRBF神经网络的训练,确定中心和权值;
2) 验证样本:用于寻找并确定最有效的模型。计算适应度函数时,将验证样本的输入信号作为模型输入,验证样本的均方误差作为差分进化算法的适应度函数,使网络可以重新调整分散度,并达到验证误差最小的状态,表示模型效果最佳;
3) 预测样本:以一组新信号构建神经网络,并用算法中计算出的宽度矩阵作为隐含层中的宽度,检验模型的精度以及泛化能力。
这种方法已经被Kou[23]验证,最后结论为由带验证信号方法训练出来的模型比无验证信号建模具有更高的精度与泛化能力。
2 算例为验证模型的可行性以及高泛化能力,选取NACA0012翼型作为研究对象,计算在Ma=0.8、翼型绕25%弦长处做俯仰运动的升力系数以及力矩系数。模型采用单输入单输出方式,由CFD计算所得的俯仰位移作为函数输入,通过两层映射后,分别输出升力系数与力矩系数。经验证,此模型比单输入多输出模型具有更高计算精度、更小预测误差、更强的泛化能力。本部分有两组预测信号,分别为机翼做随机运动以及周期运动时的位移输入和升力、力矩系数输出。样本信号有1000个样本点。选取俯仰运动最大幅值A为0.29°、1.15°、2.87°和5.73°(弧度单位分别为0.005、0.02、0.05、0.1) 的随机或简谐运动数据,数据涵盖从完全线性、弱非线性到强非线性的特性。预测算例中的简谐运动选取减缩频率ks=0.1635,无量纲时间步长为0.4。无量纲时间步长DT计算公式为:
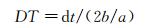
|
(6) |
dt为物理时间步长,b为半弦长,a为自由来流声速。简谐信号一周期内有60个无量纲时间步长。预测随机运动时,使用最大俯仰角度为8.59°的信号训练,并使用最大俯仰角度为0.29°的小幅高频信号作为验证信号。经对比,对升力系数而言,延迟阶数m、n均为3时得到最优模型;而由于力矩更强的非线性特征,故选择延迟阶数m、n为4。
在构建气动力模型时,差分进化算法中的变异因子F=0.4,交叉因子CR=0.6,进化代数G=300,种群个数Size=40。在神经网络模型中每隔20个样本固定选择一个中心,可以形成50个中心的模型结构,待优化宽度为50个。
2.1 随机信号预测结果预测信号是Ma=0.8时最大俯仰角度为A=5.73°、A=2.87°、A=1.15°、A=0.29°的随机运动。输出为升力系数与力矩系数。
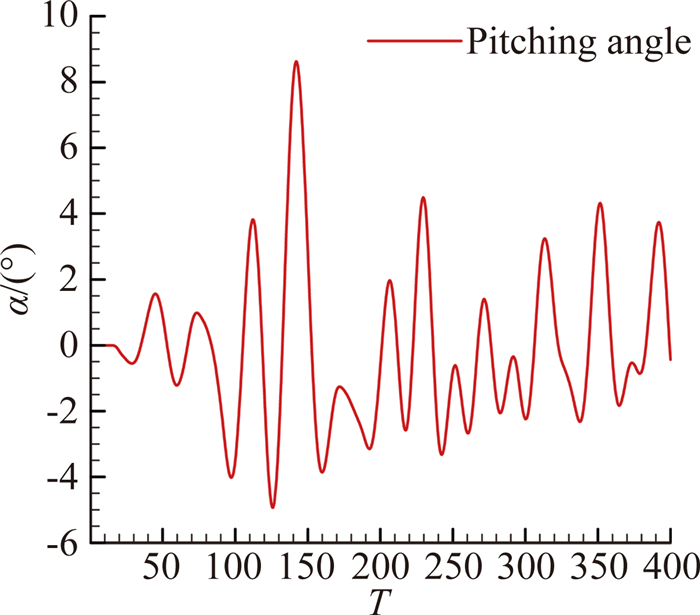
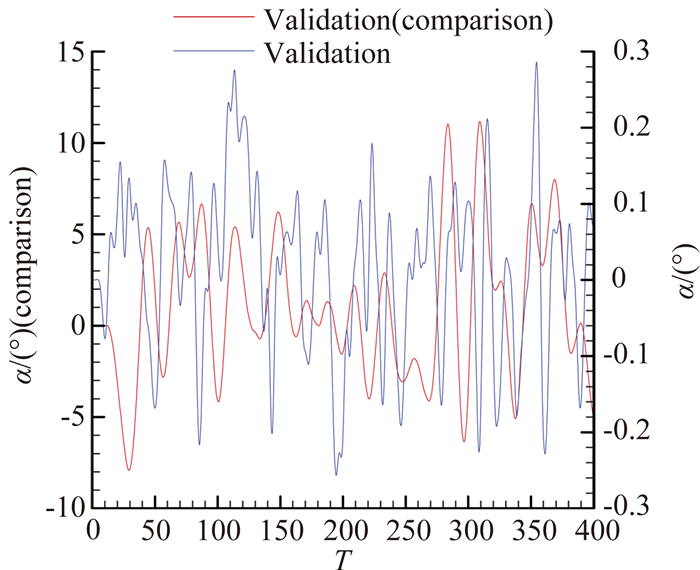
2.1.1 训练信号与验证信号图 4为训练信号,采用NACA0012机翼大幅单自由度随机运动,最大俯仰角为8.59°,使模型能够学习结构大振幅非线性时的气动力,且训练信号在减缩频率0至0.4之间具有较强的能量。而图 5展示了两种验证信号,分别为小幅高频运动与大幅随机运动。模型采用结构小幅高频信号,以兼顾结构在微幅运动时的线性气动力信息的学习。验证信号频带更宽,在减缩频率0至0.8之间具有较强的能量,涵盖了针对的非定常气动力问题的频率。对比组中,模型采用大幅运动信号作为验证信号,以展示模型在两种不同验证信号下的泛化能力。
|
| 图 4 训练信号A=8.59° Fig. 4 Training signal A=8.59° |
|
| 图 5 两组验证信号 Fig. 5 Validation signal and its comparison |
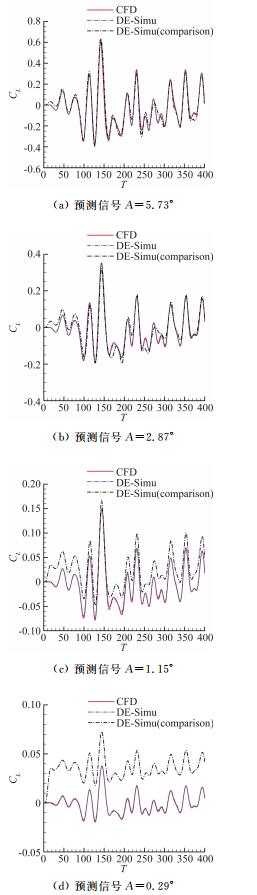
图 6、图 7中DE-Simu为用小幅高频信号作为验证信号的模型输出,DE-Simu (comparison) 为同等条件下使用大幅信号验证的模型输出,文献[23]中使用的是这种信号。该文献中并没有对验证信号的选取进行研究,而本文将针对不同验证信号的选取而进行讨论。结果选取了用小幅高频信号验证与大幅信号验证对同一预测信号的预测结果作比较,以对比模型选取不同验证信号而获得不同的泛化能力。
|
| 图 6 随机运动升力系数的对比结果 Fig. 6 Comparison of lift coefficient in random motion |
|
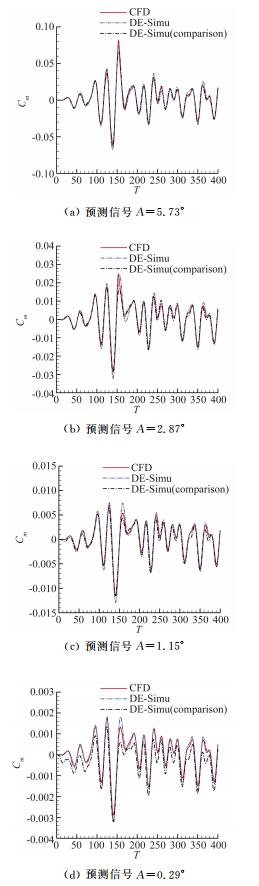
| 图 7 随机运动力矩系数的对比结果 Fig. 7 Comparison of moment coefficient in random motion |
2.1.2 升力系数预测结果
图 6展示了位移不断减小的情况下,模型辨识非线性气动力与线性气动力的能力。图 6(a)中三条曲线基本吻合,而对比信号组偶尔有辨识不精确的情况,说明了带小幅高频验证信号的DE-RRBFNN模型对非线性气动力辨识效果更好。随着信号非线性的减弱,对比信号组逐渐与另外两组产生了较大偏差,如图 6(b)和图 6(c)。如图 6(d), 最终在预测最小俯仰角时,对比信号组曲线已和其他两条曲线完全分离,而此时引入较小俯仰角验证信号所预测的结果与CFD计算解吻合得很好。表 1给出了随机运动升力系数相对误差。
| A | Error (validated by small-amplitude signal) | Error (validated by large-amplitude signal) |
| 5.73° | 0.0976 | 0.2214 |
| 2.87° | 0.0573 | 0.3158 |
| 1.15° | 0.0533 | 0.9855 |
| 0.29° | 0.0872 | 4.6423 |
2.1.3 力矩系数预测结果
图 7表明了模型对于气动力矩的辨识能力。与预测升力系数相似,在辨识非线性气动力时,引入大幅验证信号和小幅验证信号的辨识结果没有明显差别。而随着俯仰角的减小,信号线性的增强,引入较小俯仰角的模型具有了较大的精度,这点从图 7(d)以及表 2的内容中可以看出。值得注意的是,在预测较大幅度的运动时,验证信号的不同对模型精度并没有明显改变。但是在辨识小运动幅度的气动力矩时,可以体现出引入较小俯仰角验证信号的优势。
| A | Error (validated by small-amplitude signal) | Error (validated by large-amplitude signal) |
| 5.73° | 0.1795 | 0.1571 |
| 2.87° | 0.1838 | 0.1955 |
| 1.15° | 0.1605 | 0.2182 |
| 0.29° | 0.1836 | 0.6369 |
通过以上可以发现使用小幅高频验证信号所得到的模型要优于使用大幅验证信号所得的模型。
通过对随机运动的气动力预测可以得出:引入小幅验证信号对增强神经网络模型辨识线性气动力系数以及力矩系数的能力有很大帮助,进一步的增加了模型对不同运动幅度信号的泛化能力。
2.2 简谐信号预测结果本小节采用Ma=0.8时减缩频率ks=0.1635的简谐运动进行模型测试,振幅分别为A=5.73°、A=2.87°、A=1.15°、A=0.29°。输出为升力系数与力矩系数,预测简谐运动的训练信号与之前给出的训练信号相同。
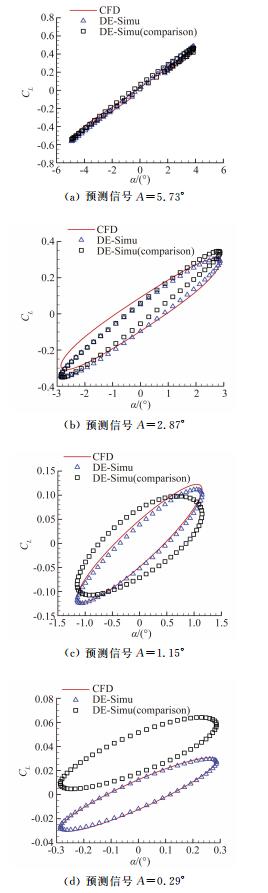
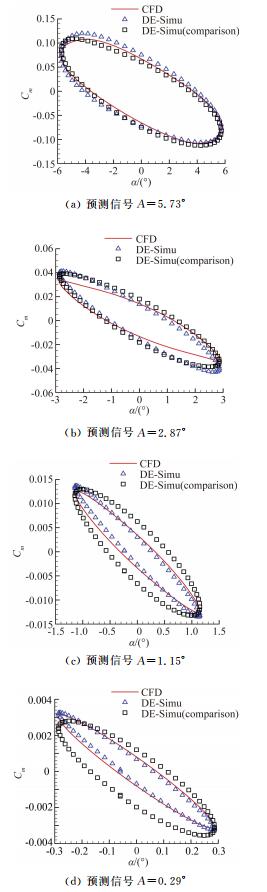
图 8、图 9展现了模型对简谐信号的预测能力。与辨识非线性气动力结果类似,图 8(a)中两模型在辨识大幅信号时没有明显区别。随着信号振幅的减小,引入小幅验证信号的优势可以明显体现。从图 8(b)至图 8(d)可以看出小幅验证信号所辨识的结果与CFD计算解更加贴合。而图 8(a)的迟滞环滞回空间小是因为该状态靠近做功转换临界点,振幅小于该状态时,迟滞环为逆时针,气动力做负功;振幅大于临界点时,迟滞环变为顺时针,气动力做正功。临界点状态附近的状态由于各种外力因素的作用而滞回空间小,但并非接近定常状态。对于辨识的力矩系数,从图 9(a)至图 9(d)中可以看出,随着振幅减小,引入小幅验证信号的结果要明显优于大幅验证信号。
|
| 图 8 简谐运动升力系数的对比结果 Fig. 8 Comparison of lift coefficient in harmonic motion |
|
| 图 9 简谐运动力矩系数的对比结果 Fig. 9 Comparison of moment coefficient in harmonic motion |
| A | Error (validated by small-amplitude signal) | Error (validated by large-amplitude signal) |
| 5.73° | 0.0515 | 0.0755 |
| 2.87° | 0.1529 | 0.2316 |
| 1.15° | 0.0927 | 0.3668 |
| 0.29° | 0.0400 | 1.7491 |
| A | Error (validated by small-amplitude signal) | Error (validated by large-amplitude signal) |
| 5.73° | 0.0956 | 0.1007 |
| 2.87° | 0.2701 | 0.1995 |
| 1.15° | 0.1105 | 0.2508 |
| 0.29° | 0.0732 | 0.2993 |
综上,使用小幅高频信号作为验证信号的模型都具有与用大幅验证信号相近或更高的输出精度。尤其是在小幅线性运动预测时,使用小幅验证信号的优势极为突出。从宽度角度解释,引入的小幅高频验证信号调整了神经网络模型中隐含层中的宽度,即隐含层中宽度的确定不单单依赖于大幅训练信号的特性,同时也依赖于验证信号中小幅信号的特性,两者一同决定在给定中心下的最优宽度。所以最后小幅验证信号的结果优于大幅验证信号,这种建模方法进一步增强了模型的泛化能力。
3 结论本文发展了一种基于CFD的RRBF神经网络气动力模型,通过引入验证信号改进了模型泛化能力。该模型以翼型俯仰运动的位移为输入,分别输出升力系数或力矩系数,并引入输出反馈以体现非定常流场的动态效应。神经网络采用固定间隔的中心选择,并且使用差分进化算法优化每个神经元的宽度以调整模型的泛化能力。算法优化目标为使得验证信号的预测精度最高。预测算例采用了跨声速下NACA0012翼型的随机和简谐俯仰运动,以对比不同验证信号对模型精度的影响,及这种模型对于不同振幅下非定常流场动态特征的泛化能力。算例表明当采用小幅高频验证信号时,模型对于大幅运动下的强非线性特征和小扰动下的动态线性特点均具有更高的预测精度,因此发展的这种DE-RRBFNN模型总体上能够把握非定常气动力的主要特征,且耗时远低于CFD计算。
| [1] | Dowell E H. Eigenmode analysis in unsteady aerodynamics: reduced order models[J]. AIAA Journal, 1996, 34(8): 1578–1583. DOI:10.2514/3.13274 |
| [2] | Silva W A. Identification of linear and nonlinear aerodynamic impulse responses using digital filter techniques. AIAA-97-3712[R]. Reston: AIAA, 1997. |
| [3] |
Zhang W W, Ye Z Y. On unsteady aerodynamic modeling based on CFD technique and its applications on aeroelastic analysis[J].
Advances in Mechanics, 2008, 38(1): 77–86.
(in Chinese) 张伟伟, 叶正寅. 基于CFD的气动力建模及其在气动弹性中的应用[J]. 力学进展, 2008, 38(1): 77–86. DOI:10.6052/1000-0992-2008-1-J2006-158 |
| [4] | Hall K C, Thomas J P, Dowell E H. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows[J]. AIAA Journal, 2000, 38(10): 1853–1862. DOI:10.2514/2.867 |
| [5] | Raveh D E. Reduced-order models for nonlinear unsteady aerodynamics[J]. AIAA Journal, 2001, 39(8): 1417–1429. DOI:10.2514/2.1473 |
| [6] | Zhang W W, Ye Z Y, Zhang C A. ROM based aeroservoelastic analysis in transonic flow[J]. Journal of Aircraft, 2009, 46(6): 2187–2183. |
| [7] | Glaz B, Liu L, Friedmann P P. Reduced order nonlinear unsteady aerodynamic modeling using a surrogate based recurrence framework[J]. AIAA Journal, 2010, 48(10): 2418–2429. DOI:10.2514/1.J050471 |
| [8] | Marquez F D, Anderson J. Identification and prediction of unsteady transonic aerodynamic loads by multi-layer functionals[J]. Journal of Fluids and Structures, 2001, 15(1): 83–106. DOI:10.1006/jfls.2000.0321 |
| [9] | Thomas J P, Dowell E H, Hall K C. Nonlinear inviscid aerodynamic effects on transonic divergence, flutter, and limit-cycle oscillations[J]. AIAA Journal, 2002, 40(4): 638–646. DOI:10.2514/2.1720 |
| [10] | Lindhorst K, Haupt M C, Horst P. Efficient surrogate modelling of nonlinear aerodynamics in aerostructural coupling schemes[J]. AIAA Journal, 2014, 52(9): 1952–1966. DOI:10.2514/1.J052725 |
| [11] | Ghoreyshi M, Jirasek A, Cummings R M. Computational approximation of nonlinear unsteady aerodynamics using an aerodynamic model hierarchy[J]. Aerospace Science and Technology, 2013, 28(1): 133–144. DOI:10.1016/j.ast.2012.10.009 |
| [12] |
Shi Z W, Ni F Y, Chen Y L. The state-space models based on two-steps linear regression method[J].
Acta Aerodynamica Sinica, 2013, 31(6): 699–703.
(in Chinese) 史志伟, 倪芳原, 陈永亮. 基于两步线性回归的状态空间模型建立与验证[J]. 空气动力学学报, 2013, 31(6): 699–703. |
| [13] | Zhang W W, Wang B B, Ye Z Y. Efficient method for limit cycle flutter analysis by nonlinear aerodynamic reduced-order models[J]. AIAA Journal, 2012, 50(5): 1019–1028. DOI:10.2514/1.J050581 |
| [14] |
Wang B B, Zhang W W, Ye Z Y. Unsteady nonlinear aerodynamics identification based on Neural Network model[J].
Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1379–1387.
(in Chinese) 王博斌, 张伟伟, 叶正寅. 基于神经网络模型的动态非线性气动力辨识方法[J]. 航空学报, 2010, 31(7): 1379–1387. |
| [15] | Du H P, Zhang N. Time series prediction using evolving radial basis function networks with new encoding scheme[J]. Neurocomputing, 2008, 71(7-9): 1388–1400. DOI:10.1016/j.neucom.2007.06.004 |
| [16] | Kurkova V, Sanguineti M. Learning with generalization capability by kernel methods of bounded complexity[J]. Journal of Complexity, 2005, 21(3): 350–367. DOI:10.1016/j.jco.2004.11.002 |
| [17] |
Kou J Q, Zhang W W, Ye Z Y. Dynamic nonlinear aerodynamics modeling method based on layered method[J].
Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3785–3797.
(in Chinese) 寇家庆, 张伟伟, 叶正寅. 基于分层思路的动态非线性气动力建模方法[J]. 航空学报, 2015, 36(12): 3785–3797. |
| [18] |
Kou J Q, Zhang W W. Research on the effects of basis function widths of aerodynamic modeling based on recursive RBF neural network[J].
Advances in Aeronautical Science and Engineering, 2015, 6(3): 261–270.
(in Chinese) 寇家庆, 张伟伟. 基函数宽度对递归RBF神经网络气动力模型精度的影响研究[J]. 航空工程进展, 2015, 6(3): 261–270. |
| [19] | Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341–359. DOI:10.1023/A:1008202821328 |
| [20] | Zhao Z Q, Huang D S. A mended hybrid learning algorithm for radial basis function neural networks to improve generalization capability[J]. Applied Mathematical Modelling, 2007, 31(7): 1271–1281. DOI:10.1016/j.apm.2006.04.014 |
| [21] | Leung C, Chow T W S. Adaptive regularization parameter selection method for enhancing generalization capability of neural networks[J]. Artificial Intelligence, 1999, 107(2): 347–356. DOI:10.1016/S0004-3702(98)00115-5 |
| [22] | Ni Y Q, Zhou H F, Ko J M. Generalization capability of neural network models for temperature-frequency correlation using monitoring data[J]. Journal of Structural Engineering, 2009, 135(10): 1290–1300. DOI:10.1061/(ASCE)ST.1943-541X.0000050 |
| [23] | Kou J Q, Zhang W W. An approach to enhance the generalization capability of nonlinear aerodynamic reduced-order models[J]. Aerospace Science and Technology, 2016, 49(1): 197–208. |



