旋转的叶片, 如直升飞机的旋翼, 风力机的叶片等, 即使在定常运动时, 由于旋转的作用, 其截面受到的来流大小与迎角也会非定常变化。针对翼型的平动与非定常迎角变化问题, Theodorsen在1935年提出了非定常气动力的理论解[1]。Isaacs根据Theodorsen理论加入了来流速度变化的影响[2]与迎角变化的影响[3]。Greenberg考虑了速度脉动与翼型运动的复合作用[4]。Mateescu在2006年发展了在低速可压缩情况下非定常气动力模型[5], 模型采用在翼型前缘与脊(ridge) 上的速度奇点的解, 考察了刚性与柔性翼型的平动与转动非定常性。Walker等考虑了翼型在柔性变形情况下的气动力[6]。Ramesh发展了模型用于考察前缘涡对于昆虫飞行的影响[7]。Cho等采用3维非定常涡格(vortex lattice) 方法, 发展了非定常气动力模型, 用于考虑速度脉动引起的非定常气动力对气动弹性稳定性的影响[8]。刘启宽等[9]采用Greenberg公式分析了风力机叶片的挥舞特性。Williams等采用Greenberg模型[4]设计控制率, 抑制来流振荡引起的受力变化[10]。Jose等采用Theodorsen的理论分析了二维多段翼型间隙对非定常气动力的影响[11]。Strangfeld[12]使用NACA0018翼型通过实验对Iscaccs和Greenberg提出的模型进行了考察。实验中翼型固定, 来流速度做正弦变化。来流的平均速度为11m/s, 最大速度为16.5m/s, 最小速度为5.5m/s。在海平面条件下, 平均速度对应马赫数近似为0.0326, 流动可以近似为不可压缩流动。基于弦长的Reynolds数为2.5×105。实验考察了迎角为2°与8°时升力系数随速度的变化。在迎角为2°时实验结果振动较大。但通过前两阶Fourier模态的拟合结果与理论吻合较好。在迎角为8°时实验较光滑, 但低估了最大升力系数。这是由于迎角8°时实验中涡在翼型表面的分布与理论分布不同引起。
Isaacs和Greenberg的气动力公式采用势流理论推导。其试用范围为:二维不可压缩势流流动, 迎角α较小, 满足近似关系α≈sin(α), 来流不会反向。本文通过计算, 考察弱可压缩性对Isaacs和Greenberg模型精度的影响。文中首先重复了Strangfeld等的实验条件下升力系数随速度的变化。然后对更高马赫数0.1, 0.2和0.3时升力系数的变化进行考察。
1 Greenberg、Isaacs非定常升力系数气动力模型来流速度围绕平均速度做正弦振动时会引起翼型受到的力和力矩也随着速度变化, 做正弦变化。设来流速度u做正弦变化的表达式为:
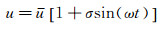
|
(1) |
其中t为时间, 来流的平均速度为u, 正弦变化的振幅为σ, 随时间变化的角频率为ω。在此来流作用下, 根据Isaacs的气动力公式, 非定常升力系数Cl(t) 与定常升力系数Cl, st之比为:
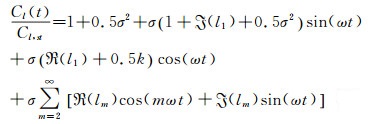
|
(2) |
其中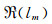
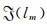
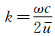
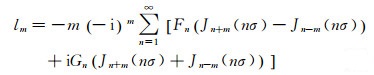
|
(3) |
级数中Jm为m阶第一类Bessel函数。Fn和Gn为:
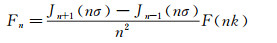
|
(4) |
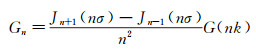
|
(5) |
函数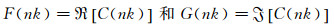
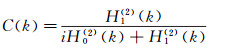
|
(6) |
式中H1(2)为2阶1次Hankel函数, H0(2)为2阶0次Hankel函数。Isaacs的理论也给出的非定常气动力产生的力矩Cm(t) 与定常情况下的气动力矩Cm, st(t) 之比:
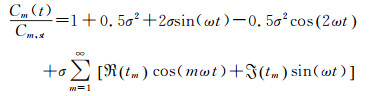
|
(7) |
Cl、Cm和lm的表达式为无穷级数, Strangfeld等[12]将Cl中的无穷级数在第8项之后(m>8) 截断; lm的级数表达式在第15项(n>15) 后截断。其误差小于10-6。
根据Greenberg模型, 非定常升力系数Cl(t) 与定常升力系数Cl, st之比为:
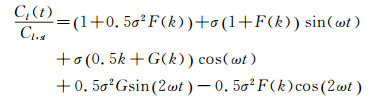
|
(8) |
其中
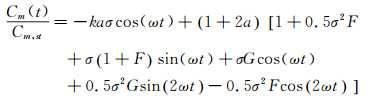
|
(9) |
式中a是取矩的点距离前缘的距离。在不可压缩无粘势流假设下, 对于翼型四分之一弦长的地方取矩, 无论迎角多少, 得到的力矩系数近似为0[16]。文中所有力矩均关于翼型的前缘取矩。
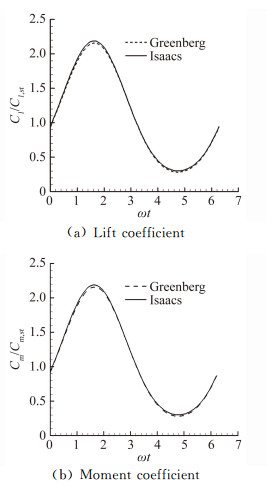
图 1为Iscaacs和Greenberg模型的比较。其中实线为Isaacs模型结果, 虚线为Greenberg模型结果。无论对于升力系数, 还是力矩系数, Greenberg公式在最低点与最高点处低估了升力。但是在初始位置与接近平衡点时两个模型结果相近。
|
| 图 1 Isaacs模型与Greenberg模型比较 Fig. 1 The comparison of Isaacs' model and Greenberg's model |
2 翼型绕流计算设置
Isaacs模型与Greenberg模型均对于不可压缩流动提出。为了与模型的适用范围接近, 本文计算采用的马赫数较低。分别考察了马赫数为0.0326、0.1、0.2和0.3时, 迎角为2°和8°的情况。其中马赫数为0.0326近似为Strangfeld实验[12]的来流条件。计算采用HUNS3D程序[13]。通量部分采用AUSM+-up格式[14], AUSM+-up格式在马赫数较低时可以保证格式的收敛性和精度[14]。湍流模型采用SA模型[15], Reynolds数为Re=2.5×105。时间推进采用双时间步方法, 其中隐式迭代采用LU-SGS方法。计算采用2维网格, 计算区域为矩形, 如图 2所示。

|
| 图 2 迎角为8°时的计算区域网格 Fig. 2 Mesh for the angle of attack at 8° |
在流向与法向方向上为40倍的翼型弦长, 出口的上下两角导圆。翼型位于计算区域中央。迎角通过翼型旋转设定。来流方向始终与入口垂直, 上下两个边界采用滑移无穿透边界条件, 使得入口下游的流场能够根据来流速度的变化进行调整, 避免人为指定带来的误差。入口边界指定速度, 其随时间的变化为式(1)。式(1) 中σ=0.5与Strangfeld等的实验[12]所用振幅相同, ω=4.72×10-3根据Strangfeld的实验[12]中约化频率k=0.0074得到。
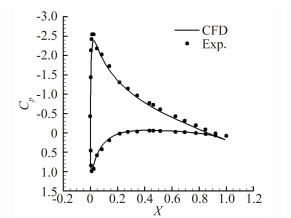
为了验证网格与计算条件的适用性, 采用程序对来流马赫数为0.0326、迎角为8°的定常情况进行计算, 并与实验进行对比。图 3为翼型表面升力系数。其中实线为计算所得结果, 点为实验结果。在翼型上表面与下表面上计算与实验吻合较好。在前缘处, 下表面得到的升力系数与实验接近。在前缘上表面和尾缘处压力略高于实验所得值, 但差别在误差范围内。
|
| 图 3 Mach为0.0326时翼型表面压力系数与实验对比 Fig. 3 Comparison of CFD calculation and the experiment of Strangfeld on the pressure coefficient |
3 非定常气动力特性分析 3.1 模型与计算比较
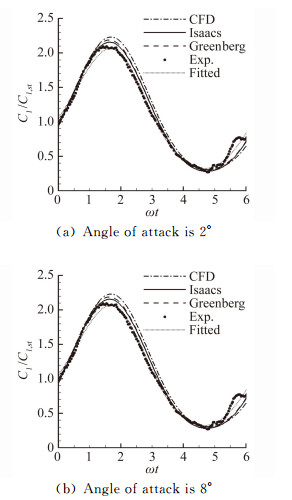
为了验证程序在非定常时的计算结果, 将计算得到的升力系数Cl、力矩系数Cm在马赫数0.0326时与实验和理论进行了比较。为了方便比较, 升力系数采用定常状态做了归一化。非定常计算从定常状态启动, 为了消除启动时初始效应对计算的影响, 结果为速度变化第二个周期时的数据。图 4、图 5中实线为Isaacs的理论结果, 虚线为Greenberg的理论结果,点划线为计算结果, 实心圆点为Strangfeld等的实验结果[12]。实验中压力传感器受到噪声的影响, 出现脉动[12]。为了减小实验时压力传感器噪声的影响, Strangfeld对其实验结果进行了2阶Fourier模态的拟合, 图中点线为Strangfeld拟合的结果。
|
| 图 4 马赫数为0.0326时的升力系数 Fig. 4 Lift coefficient at Mach number 0.0326 |
|
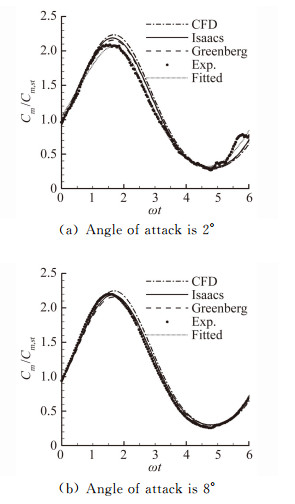
| 图 5 马赫数为0.0326时的力矩系数 Fig. 5 Moment coefficient at Mach number 0.0326 |
图 4为升力系数Cl。在2°和8°迎角时, 升力系数随迎角增长为线性关系。计算所得到的结果振幅略高于实验和理论, 在速度减小时升力系数减小相对滞后。这是由于在马赫数0.0326时流动具有弱可压缩性, 入口速度变化需要一定时间传递到翼型附近。
图 5为力矩系数Cm。力矩关于翼尖取矩。与图 4计算得到的升力系数情况相似。计算得到的力矩系数的振幅略高于模型实验相近, 但是相位落后。在马赫数0.0326时, 计算得到的非定常升力系数Cl、力矩系数Cm略高于模型和实验, 相位落后, 但误差小于5%, 满足对工程问题的分析的精度要求。
下面将采用相同的计算条件, 在马赫数提高为0.1、0.2和0.3时, 分析马赫数提高对升力系数的影响。
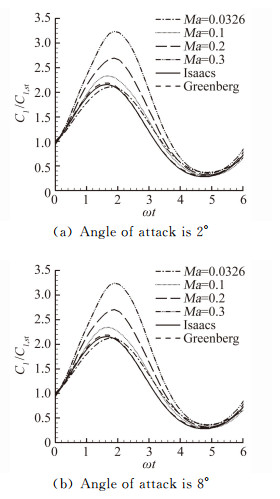
马赫数小于0.3时, 流动近似为不可压缩流动。在定常状态下, 马赫数为0.1、0.2、0.3的升力系数与马赫数为0.0326时相同。图 6为来流速度正弦振动时升力系数随时间的变化。图中比较了马赫数0.0326、0.1、0.2、0.3时非定常升力系数与Isaacs、Greenberg模型的差别。图 6(a)的迎角为2°; 图 6(b)的迎角为8°。由于当马赫数升高时, 实验的条件不再适用, 所以不将实验与计算进行比较。随着马赫数的升高, 非定常升力系数的最高点逐渐升高, 相位逐渐落后, 其中对于最大马赫数0.3时与模型的差别最大。
|
| 图 6 不同马赫数升力系数比较 Fig. 6 Lift coefficient of different Mach numbers |
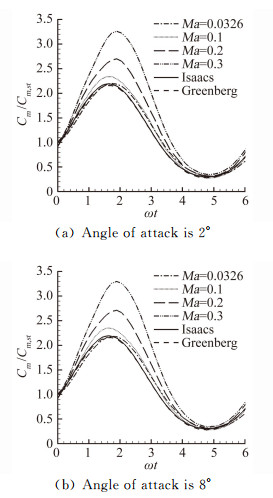
马赫数变化, 同样会引起力矩系数的变化。图 7为来流速度正弦振动时升力系数随时间的变化。随着马赫数的升高, 力矩系数与模型的差别逐渐增加。其变化趋势与升力系数相同。在最大马赫数0.3时差别对大。对于相同的马赫数, 差别最明显的位置位于速度最大的点, 即ωt=π/2。而对于速度最小的时候, ωt=3π/2时, 速度模型与计算得到的力矩系数最相近。
|
| 图 7 不同马赫数力矩系数比较 Fig. 7 Moment coefficient of different Mach numbers |
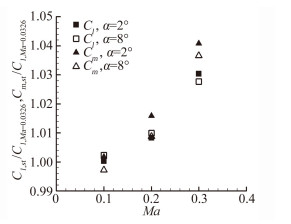
由于计算与模型考虑的是非定常情况下的升力系数、力矩系数采用了定常情况下的升力系数、力矩系数作归一化。所以图 6与图 7中马赫数引起的变化即可能为分子--非定常时升力、力矩系数的变化, 也可能是分母--定常升力、力矩系数的变化。图 8为在定常情况下将马赫数为0.1、0.2和0.3的升力与阻力系数与马赫数为0.0326的情况相比。图中方形表示升力系数之比, 三角形表示力矩系数之比。实心图形表示迎角为2°的情形, 空心图形表示迎角为8°的情况。
|
| 图 8 定常流动不同马赫数升力系数、力矩系数与马赫数0.0326时各个系数之比 Fig. 8 The rate of steady moment and lift coefficients at Mach number 0.1, 0.2, 0.3 over those at Mach number 0.0326 |
从图中可以看出, 随着马赫数的增大, 升力系数与力矩系数逐渐增大, 与马赫数为0.0326时的差别也逐渐扩大。但是误差在5%以内, 可以认为近似相等。也就是升力系数与力矩系数在定常情况下随着马赫数的增加基本保持不变。图 6和图 7中不同马赫数时升力系数与力矩系数的差别主要由于非定常部分引起。
根Isaacs的理论[2], 非定常流动产生的升力与环量和速度相关。
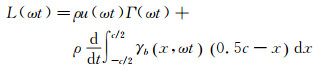
|
(10) |
式中L(ωt) 为非定常升力, Γ为绕翼型的环量, γb为受约束涡层(bound vorticity sheet), c为翼型的弦长。Isaacs的模型与Greenberg的模型考虑了速度与环量受到的非定常效应的影响。不可压缩流动假设下密度近似为常数不随压力的变化而改变。在本文计算设置下, 入口速度的变化会转化为压力的变化从而驱动流场中速度发生变化。当考虑流体的可压缩性时, 压力变化会引起密度的变化。相对翼型, 入口来流速度变化时, 也引起了来流的密度发生了变化。下面将分析在入口速度发生变化时, (10) 式中密度与来流马赫数之间的关系, 并对Isaacs的模型与Greenberg的模型进行马赫数变化引起密度变化的修正, 使其能够反映来流马赫数对非定常升力系数的影响。
3.2 弱可压缩性修正假设, 弱可压缩与不可压缩的速度与涡量场相同, 可以采用Isaacs或Greenberg模型描述。弱可压缩性仅改变了式(10) 中的密度项。设不可压缩流动假设下模型预测的升力为LI, 弱可压缩假设下得到的升力为L, 根据(10) 式得到两者之比R(ωt) 为密度之比:
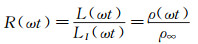
|
(11) |
式中ρ为弱可压缩时得到的流动密度, 不可压缩假设下流动的密度为来流密度ρ∞。
将密度ρ分解为两部分, 一部分为来流密度ρ∞, 一部分为流动引起的密度的变化ρ′, 即ρ=ρ∞+ρ′。将压力也分解为两部分, 一部分为来流压力p∞, 一部分为流动引起的压力变化p′, 即p=p∞+p′。在势流假设下流动沿流线满足Bernoulli定理。当马赫数小于0.3时, 定常流动近似为不可压缩。此时的压力脉动量级为:
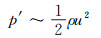
|
(12) |
为得到密度变化的比值, 引入压力变化p′与来流压力p∞的比值, 并将声速与温度关系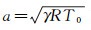
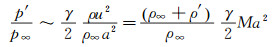
|
(13) |
式(13) 中Ma为来流马赫数, 其大小随时间在平均来流马赫数Ma附近做简偕振动, 振幅与周期和来流速度变化(1) 式相同Ma=Ma[1+σsin (ωt)]。γ/2为常数, 在量级分析中可以将此常数改为常数系数K而不影响最后得到的量级, 由此可以将式(13) 变为式(14):
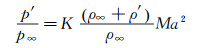
|
(14) |
根据式(12), 流场中的温度假设为常数。对于等温情况, 压力变化与来流压力之比等于密度变化与来流密度的比值:
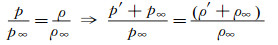
|
(15) |
将等式(15) 两边同时减去1得到。
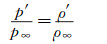
|
(16) |
将等温过程压力与密度关系式(16), 代入式(14) 得到:
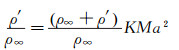
|
(17) |
化简得到:
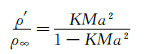
|
(18) |
将式(18) 等式两边同时加1, 并代入式(11), 得到的压力与模型中的压力的比值为:
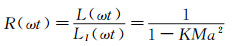
|
(19) |
由于升力系数为升力与参考面积、来流动压之比。弱可压缩假设与不可压缩假设的参考面积、来流动压相同。所以根据式(19) Isaacs、Greenberg模型预测的升力系数Cl, I与计算得到的升力系数Cl有关系式:
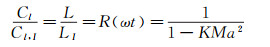
|
(20) |
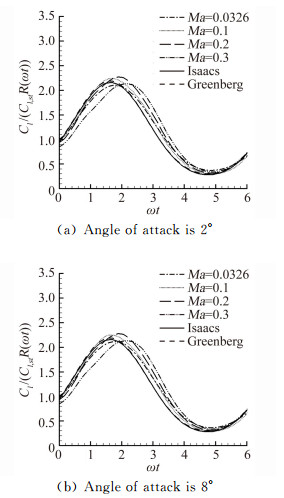
为了与模型作比较, 将迎角为2°和8°时平均来流马赫数Ma为0.0326、0.1、0.2和0.3情况下得到的升力系数曲线除以式(20)R(ωt), 若曲线重合则修正关系式可用。关系式R(ωt) 中的系数K可以通过最小二乘法得到, 当K=1.8时对于各个平均来流马赫数Ma的情况, 计算与模型误差较小。图 9(a)和(b)为升力系数通过修正的结果。与未修正的情况相比, 在来流马赫数升高的过程中, 修正减小了幅值误差。在马赫数最低点附近(ωt=3π/2), 模型与计算相近, 修正对这部分没有改变。在马赫数最高点时(ωt=π/2), 修正减小了模型计算的差别, 使得误差在5%以内。从图中还可以看出随着平均来流马赫数的升高, 相位逐渐落后。这是马赫数升高使得压缩性明显, 入口的速度变化需要更长的时间才能够传导到翼型上。而模型假设来流为不可压缩, 入口速度变化反映到翼型上的时间几乎为0。
|
| 图 9 升力系数可压缩性修正 Fig. 9 Compressibility correction of the Isaacs' and Greenberg's model |
力矩为压力与矩心距离乘积的积分, 不可压缩与弱可压缩情况力矩系数采用的无量纲化系数相同, 因此力矩系数之比等于压力之比。根据式(15) 与式(11), 不可压缩与可压缩时的压力之比等于升力之比R(ωt)。
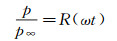
|
(21) |
所以力矩之比为:
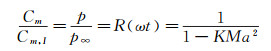
|
(22) |
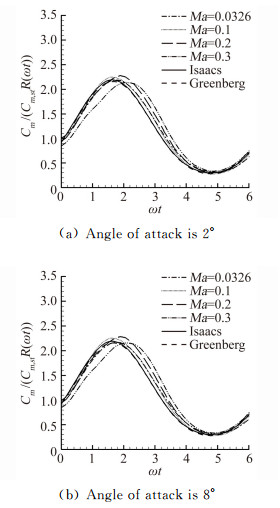
将迎角为2°和8°时马赫数为0.0326、0.1、0.2和0.3情况下得到的力矩系数除以式(20)R(ωt) 得到图 10。R(ωt) 中的系数K同样取为K=1.8。与升力系数情况相同, 修正使得力矩系数变化的幅值与模型相差在5%以内。
|
| 图 10 力矩系数可压缩性修正 Fig. 10 Compressibility correction of the Isaacs' and Greenberg's model for moment coefficient |
4 结论
本文采用计算方法, 针对NACA0018翼型, 在来流马赫数分别为0.0326、0.1、0.2和0.3时得到了非定常升力系数随时间的演化。发现:
1) 在马赫数0.0326时计算结果与Isaacs的模型、Greenberg的模型以及Strangfeld等[12]在2014年实验的误差在5%以内。
2) 随着马赫数的升高, 计算与Isaacs的模型、Greenberg的模型的差别逐渐增加, 在马赫数0.3时差别最大, 最大相差50%。
3) 通过考虑入口附近速度变化引起的密度变化, 修正翼型的来流密度, 使得计算结果与Isaacs的模型、Greenberg的模型差别在5%左右。
致谢: 感谢西北工业大学王刚教授、刘毅博士在本文工作中给予作者的帮助与建议。| [1] | Theodorsen T. General theory of aerodynamic instability and the mechanism of flutter[R]. NACA Rep No. 496, 1935:413-433. |
| [2] | Isaacs R. Airfoil theory for flows of variable velocity[J]. Journal of the Aeronautical Sciences, 1945, 12(1):113–117. DOI:10.2514/8.11202 |
| [3] | Isaacs R. Airfoil theory for rotary wing aircraft[J]. Journal of the Aeronautical Sciences, 1946, 13(4):218–220. DOI:10.2514/8.11351 |
| [4] | Greenberg J M. Airfoil in sinusoidal motion in a pulsating stream[R]. NACA TN1326, 1947. |
| [5] | Mateescu D, Neculita S. Low frequency oscillations of thin airfoils in subsonic compressible flows[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2006. |
| [6] | William P Walker, Mayuresh J Patil. Unsteady aerodynamics of deformable thin airfoils[J]. Journal of Aircraft, 2014, 51(6):1673–1680. DOI:10.2514/1.C031434 |
| [7] | Ramesh K, Gopalarathnam A, Edwards J R, et al. Theoretical analysis of perching and hovering maneuvers[R]. AIAA 2013-3194. |
| [8] | Cho S H, Kim T, Song S J. Freestream Pulsation Effects on the Aeroelastic Response of a Finite Wing[J]. AIAA Journal, 2008, 46(11):2723–2729. DOI:10.2514/1.33731 |
| [9] |
Liu Q, Li L, Zhang Z, et al. Flapwise characteristics of a wind turbine blade with large deflection[J].
Journal of Dynamics and Control, 2012, 10(2):171–177.
(in Chinese) 刘启宽, 李亮, 张志军, 等. 风力机叶片大挠度挥舞振动特性分析[J]. 动力学与控制学报, 2012, 10(2) : 171–177. |
| [10] | Williams D, Quach V, Kerstens W, et al. Low-Reynolds number wing response to an oscillating freestream with and without feed forward control[R]. AIAA 2009-143. |
| [11] | Jose A I, Baeder J D. Steady and unsteady aerodynamic modeling of trailing edge flaps with overhang and gap using CFD and lower order models[R]. AIAA 2009-1071. |
| [12] | Strangfeld C, Müller-Vahl H, Greenblatt D, et al. Airfoil subjected to high-amplitude free-stream oscillations:theory and experiments[C]//7th AIAA Theoretical Fluid Mechanics Conference, Atlanta, GA, 2014. |
| [13] | Mian H H, Gang Wang, Raza M A. Application and validation of HUNS3D flow solver for aerodynamic drag prediction cases[C]//Proceedings of 201310th International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 2013:209-218. |
| [14] | Liou Meng Sing. A sequel to AUSM, Part Ⅱ:AUSM+-up for all speeds[J]. Journal of Computational Physics, 2006, 214:137–170. DOI:10.1016/j.jcp.2005.09.020 |
| [15] | Spalart P R, Allmaras S R. A one-equation turbulence model for Aerodynamic flows[J]. Le Recherche Aerospatiale, 1994, 1:5–21. |
| [16] | Katz J, Plotkin A. Low-speed aerodynamics[M]. Cambridge, Cambridge University Press, 2001. |



