随着军用直升机对声隐身能力要求的提高和适航条例对民用直升机噪声水平的严格限制,直升机噪声成当前的研究热点,而其中旋翼气动噪声是直升机噪声研究领域中最主要的研究对象。直升机高速平飞时,旋翼前行桨叶桨尖马赫数达到跨声速,会产生强烈的高速脉冲噪声,而高速脉冲噪声一旦出现即会占据主导地位[1-2],对直升机远场噪声产生严重辐射干扰作用。
研究表明旋翼跨声速高速脉冲噪声特性和低桨尖马赫数下的旋翼气动噪声特性存在明显差异,主要体现在HIS (high-speed impulsive) 噪声中四极子噪声的形态和辐射强度发生了明显变化。为此,一些学者对旋翼跨声速流场和声场特性展开了一系列研究。Isom[3]对旋翼非线性跨声速声场进行了初步研究,Schmitz[4]、Hawking[5]、Shenoy[6]研究了高桨尖马赫数下的离域化现象。上述研究表明桨叶表面激波扩散至桨尖外部的超声速区域时,激波干扰可能会传播至远场,桨叶表面发生离域化现象,对旋翼远场噪声产生较为强烈的辐射干扰作用。上述工作虽在旋翼跨声速声场机理研究方面取得了一些定性结论,但是未通过准确的旋翼跨声速声场求解方法来进行定量分析。在旋翼气动噪声预估方法研究方面,Ffowcs和Hawkings[7]基于Lighthill声学类比法发展了旋翼线性气动噪声预估理论,Farassat和Brentner发展了基于CFD (Computation Fluid Dynamics) 的Kirchhoff方法来预测旋翼HSI噪声[8],但是Kirchhoff方法不仅需要求解压力梯度项,而且对声源积分面选取要求很高,严格要求在线性区内才能成立,这对积分面位置的选取提出严峻挑战。近年来,Francescantonio[9]则首次采用“可穿透积分面”来求解FW-H (Ffowcs Williams-Hawkings) 方程,得到了FW-H方程新的求解方法:FW-H_pds方法(“pds”是“penetrable data surface”的简称),该方法的积分面在线性区和非线性区均成立,具有更好的鲁棒性,减轻了积分面选取的困难。韩忠华[10]对上述两种噪声求解方法进行了分析比较,同样得到了基于可穿透积分面的FW-H方法鲁棒性更好的结论。
旋翼降噪技术已经成为直升机技术研究领域内的最新热点之一。研究发现采用新型桨尖的旋翼在降低旋翼气动噪声方面具有一定潜力,许多先进的旋翼桨尖外形得到了实际应用。UH-60A“黑鹰”直升机和AH-64“阿帕奇”直升机均采用了桨叶尖部后掠的气动外形设计,著名的BERP旋翼和ERATO旋翼均采用了前掠和后掠组合桨尖[11],研究表明这一设计可以有效改善旋翼气动噪声特性。西北工业大学的宋文萍[12]、王立群[13]等采用CFD/Kirchhoff方法对后掠桨尖的气动噪声特性进行了定量分析,获得了一些有意义的结论。南京航空航天大学设计的CLOR系列外形桨尖通过数值模拟和试验研究,表明改型桨尖同样也具备一定的降噪潜力[14-15]。本文提取上述先进旋翼桨尖中前掠和后掠形式两个关键要素,拟通过先进的噪声预测手段,探索不同外形参数的后掠和前掠桨尖旋翼在抑制旋翼跨声速特性方面的影响规律。
鉴于此,本文将建立基于CFD/FW-H_pds方法的旋翼高速脉冲噪声求解方法,拟通过对UH-1H模型旋翼的跨声速噪声的计算验证该方法的有效性。在此基础上,拟研究旋翼在不同桨尖马赫数下的离域化现象以及高速脉冲噪声特性,再进一步研究了不同外形参数的后掠和前掠桨尖旋翼在抑制旋翼跨声速特性方面的影响规律,从而为现代低噪声旋翼的气动外形设计提供理论依据。
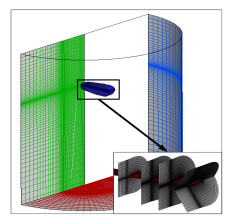
1 旋翼跨声速气动噪声计算方法 1.1 旋翼悬停流场数值模拟方法网格是CFD技术的基础。本文首先通过求解泊松方程来生成围绕翼型剖面的网格,然后桨叶段网格通过展向剖面间插值完成,最后采用绕翼型中弧线翻折策略生成桨叶的C-O型结构网格。本文背景网格采用半圆柱形结构网格。同时,采用“透视图”挖洞方法[16]来解决背景网格和桨叶网格之间的嵌套关系,并结合逆映射(Inverse Map) 方法和伪贡献单元搜寻法(PSSDE)[17]对背景网格洞边界单元的贡献单元进行快速搜寻。背景网格和桨叶网格之间流场信息传递采用三线性插值算法。本文计算采用的桨叶网格大小为247×40×76,背景网格大小为181×221×143。图 1为本文建立的嵌套网格系统示意图。
|
| 图 1 悬停状态旋翼嵌套网格系统示意图 Fig. 1 Schematic of embedded grid system around rotor in hover |
然后求解悬停状态旋翼流场,在随叶坐标系上建立以绝对物理量为参数的守恒的积分形式的RANS方程,方程如下:
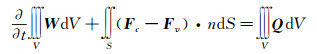
|
(1) |
其中,向量W为守恒变量、Q为由旋转带来的源项、Fc和Fv分别为无黏通量和黏性通量,其表达式分别为:
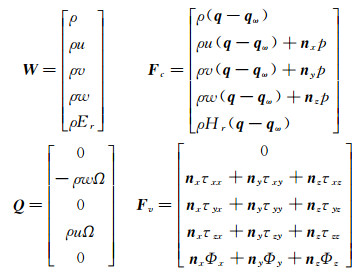
|
(2) |
式中,S为控制体表面积,V为控制体体积,n=[nx ny nz]T为单元表面法矢量。Er、Hr、p和ρ分别为气体总转能、总转焓、压强和密度。Ω为桨叶旋转角速度,q=[u, v, w]T为绝对速度,qω=[uω, vω, wω]T为牵连速度。
黏性应力τ的各分量以τxx、τxy和Φx为例,分别定义如下:
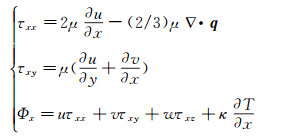
|
(3) |
式中,μ、κ、T分别为黏性系数,热传导系数和绝对温度。
黏性系数计算采用Baldwin-Lomax[18]湍流模型。桨叶表面采用无滑移条件,同时采用周期对称边界条件来模拟桨叶之间的干扰影响。为了提高流场求解的效率,本文的时间推进方法采用高效的隐式LU-SGS格式。空间离散采用有限体积法,对于交界面上的对流通量,采用高精度的Roe-MUSCL格式计算无黏通量。为避免Roe格式中可能产生的非物理解,引入Harten熵修正[19]。
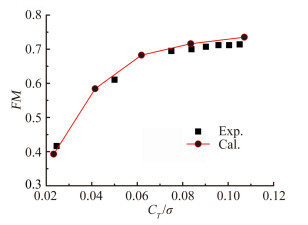
为验证本文数值方法在旋翼悬停状态气动特性计算方面的有效性,针对UH-60A后掠桨尖旋翼在桨尖马赫数为0.612的悬停状态进行了计算。图 2给出了UH-60A旋翼气动性能曲线,其中FM表示旋翼悬停效率,CT表示拉力系数,σ表示旋翼实度。计算结果与试验值[20]吻合较好,表明本文数值方法可以有效计算悬停状态旋翼的气动特性,采用该方法进行新型桨尖外形对旋翼流场的分析是有效的。
|
| 图 2 UH-60A旋翼悬停性能的计算值和试验值的比较 Fig. 2 Comparison of the calculated performance of UH-60A rotor with experimental data |
1.2 旋翼气动噪声计算方法
在上述CFD方法计算的流场基础上,本文采用基于可穿透旋转积分面的FW-H_pds方法来计算旋翼在高桨尖马赫数下的气动噪声。FW-H_pds方法将经典FW-H方程的积分面重新解释为可穿透积分面,FW-H_pds方法基于可穿透积分面的F1A公式可写为:
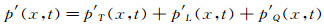
|
(4) |
其中,
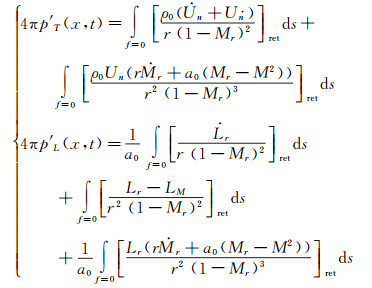
|
(5) |
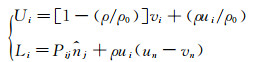
|
(6) |
式中:p′、p′ T、p′ L和p′ Q分别表示总声压、单极子噪声声压、偶极子噪声声压和四极子声压;f、x和t分别表示积分面、观察者位置和接收时间;ρ、c分别表示密度和声速;M、s、u、v分别表示马赫数、面积、扰动速度和运动速度;Pij代表应力张量;下标“0”表示未扰动量,下标“n”表示在法向的投影,下标“ret”表示延迟时间,下标“i”和“j”分别表示在i方向和j方向的投影,上标“·”表示对时间的导数。
当选取积分面位置远离物面的时候,所计算出来的结果可以认为是包含了四极子噪声的总噪声。当积分面选取为桨叶表面时,所求得到的声压为包含厚度噪声和载荷噪声的线性噪声。四极子噪声声压可以通过总噪声声压减去线性噪声声压获得。本文选取桨叶的某层网格面作为声源积分面,声源面随桨叶转动,声源面的输入参数从流场中直接获得。
2 旋翼跨声速流场及声场特性计算UH-1H旋翼悬停噪声试验[21]是旋翼气动噪声领域最为常用的验证算例之一,该试验测量了UH-1H模型旋翼在多个桨尖马赫数下桨盘平面内的无升力悬停噪声数据以供理论计算对比。该试验通过提高悬停状态旋翼桨尖马赫数,来体现大前进比状态下才会出现的旋翼跨声速声场特性。UH-1H模型旋翼为七分之一缩比模型,桨叶的展弦比为13.71,半径为1.045m,两片桨叶,无负扭转,采用单一翼型NACA0012。
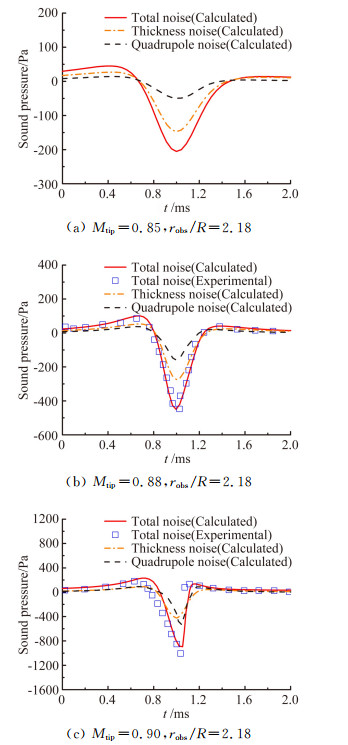
图 3(a)、(b)和(c)为UH-1H模型旋翼在桨尖马赫数分别为0.85、0.88和0.9时的厚度噪声、四极子噪声和总噪声声压时间历程对比,观察点位置在桨盘平面内距离旋转中心2.18倍半径处。Mtip表示桨尖马赫数,robs表示观察点距离旋转中心的距离,R表示旋翼半径。从图 3(b)和(c)中计算值与试验值的对比结果可以看出,本文建立的旋翼气动噪声计算方法可以有效地计算旋翼跨声速噪声特性。
|
| 图 3 UH-1H模型旋翼不同桨尖马赫数下的声压时间历程 Fig. 3 Time history of sound pressure of UH-1H rotor model at various tip Mach number |
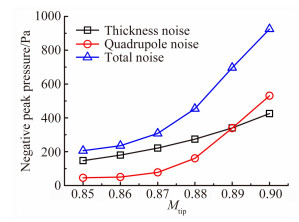
图 4展现了桨尖马赫数从0.85逐渐增大为0.90时的厚度噪声、四极子噪声和总噪声负压峰值。旋翼跨声速状态下的HSI噪声主要是由单极子源引起的厚度噪声以及四极子源引起的非线性噪声。厚度噪声负压峰值随着桨尖马赫数的增加基本呈现线性增加的规律,当桨尖马赫数较低时,厚度噪声在总噪声中占主要部分;而四极子噪声在桨尖马赫数低于0.88时增长缓慢,但是当桨尖马赫数超过0.88时,四极子噪声负压峰值突增,甚至当桨尖马赫数达0.90时,四极子噪声大小甚至超过厚度噪声。从图 3中对比可以看出,在三个不同桨尖马赫数下,厚度噪声声压波形呈现左右对称形态。而对于四极子噪声来说,桨尖马赫数为0.85和0.88时,四极子噪声声压波形左右大致对称,但是当桨尖马赫数达0.90时,四极子噪声声压波形呈现左右非对称形态,导致总噪声声压波形也呈现一定的非对称性。
|
| 图 4 UH-1H模型旋翼不同桨尖马赫数下的负压峰值 Fig. 4 Negative peak pressure of UH-1H rotor model at various tip Mach number |
为了揭示旋翼跨声速噪声产生机理,定义当地马赫数ML(local Mach number),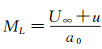
显然ML的大小由旋翼转速ω,距离旋转中心的距离r和扰动速度u决定。当r增加时,ML会大于1,由于远离桨尖,此时u≈0, a≈a0,则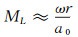
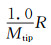
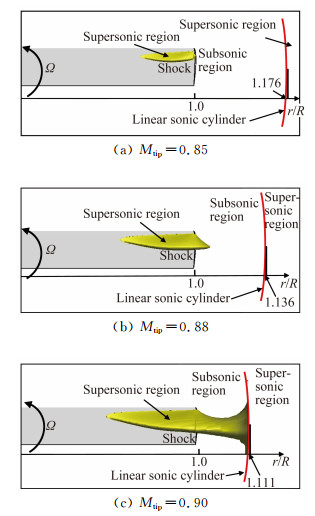
图 5(a)、(b)和(c)显示了桨尖马赫数为0.85、0.88和0.90时桨叶附近的超声速流动区域。所对应的声速分界面半径分别为1.176R、1.136R和1.111R。当桨尖马赫数为0.85时,桨叶表面超声速流动区域被限制在桨叶半径范围之内;当桨尖马赫数达到0.88时,桨叶表面产生的超声速流动区域扩散至旋翼半径之外,但是仍然没有影响到声速分界线以外的区域;当桨尖马赫数继续增加到0.90时,桨叶对周围流速扰动加大,桨叶表面的超声速区域明显影响到了声速分界线以外的超声速区域,激波扰动将会传播至远场,此时发生了严重的跨声速离域化现象。综合图 3的声压时间历程结果来看,高桨尖马赫数时桨叶表面激波扩散至桨尖外部的超声速区域是旋翼跨声速离域化现象的产生原因;随着桨尖马赫数的增加,包含四极子噪声的高速脉冲噪声辐射愈加强烈,离域化现象愈加明显。
|
| 图 5 不同桨尖马赫数时的桨盘平面超声速流动区域 Fig. 5 Supersonic region on the rotor plane at various tip Mach number |
3 新型桨尖外形参数影响机理分析
直升机旋翼桨尖对旋翼气动特性和性能有着至关重要的影响,不同桨尖旋翼的跨声速特性也不尽相同,本文拟通过对比各种前掠、后掠桨尖的高速脉冲噪声特性,研究新型桨尖在抑制旋翼跨声速特性方面的作用机理。以UH-1H缩比模型旋翼为基准,改变桨尖外形,设计了不同外形参数的后掠和前掠桨叶。计算状态:悬停无升力状态,桨尖马赫数为0.9,此时的桨尖相对来流情况与大速度前行桨叶的来流条件相似(典型的旋转桨尖马赫数0.65和前进比0.38时,前行桨叶局部来流马赫数达到0.9) 噪声观察位置为桨盘平面内距离旋转中心2.18R处。表 1和表 2分别给出了设计的后掠和前掠桨尖的参数与代号。
 |
10° | 20° | 30° |
| 0.95R | SB01 | SB02 | SB03 |
| 0.85R | SB04 | SB05 | SB06 |
 |
10° | 20° | 30° |
| 0.95R | SF01 | SF02 | SF03 |
| 0.85R | SF04 | SF05 | SF06 |
3.1 桨尖后掠的参数影响分析
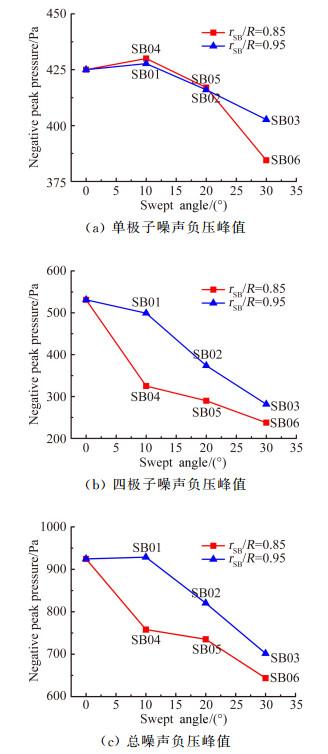
图 6(a)、(b)和(c)分别给出了不同后掠位置时厚度噪声负压峰值、四极子噪声负压峰值和总噪声负压峰值随后掠角的变化,其中rSB表示后掠起始位置。观察图 6发现,总噪声负压峰值的变化趋势和四极子噪声负压峰值的变化趋势一致,后掠桨叶对单极子声源项引起的厚度噪声影响不大。另外,厚度噪声大小随后掠位置和后掠角度的变化均不是单调变化的,且SB01和SB04桨叶厚度噪声负压峰值均略高于矩形桨叶。从图 6(b)和(c)中可以看出,后掠位置固定时,负压峰值总体上随着后掠角的增大而较小,这和文献[12-13]的结论一致;后掠角固定时,负压峰值总体上随着后掠位置靠桨叶内侧而减小。观察SB01桨叶可以发现,它的四极子噪声负压峰值、厚度噪声负压峰值和矩形桨叶接近,结果导致总噪声负压峰值略高于矩形桨叶的负压峰值。图 7给出了不同外形参数的后掠桨叶的等马赫数云图。SB01的等马赫数线云图和矩形桨叶相似,这也可以是图 6(b)中SB01桨叶的四极子噪声负压峰值和矩形桨叶接近的原因。而后掠角为30°的SB03和SB06桨叶中桨叶表面超声速流动区域对半径之外的空间区域影响最弱,这也可以解释图 6(b)中SB03和SB06桨叶四极子噪声负压峰值最小的现象。其中,相比于矩形桨叶,SB06的四极子噪声负压峰值降低幅度达56.6%。
|
| 图 6 不同后掠桨尖旋翼的噪声负压峰值比较 Fig. 6 Comparisons of negative peak pressure of rotors with various sweep-back blades |
|
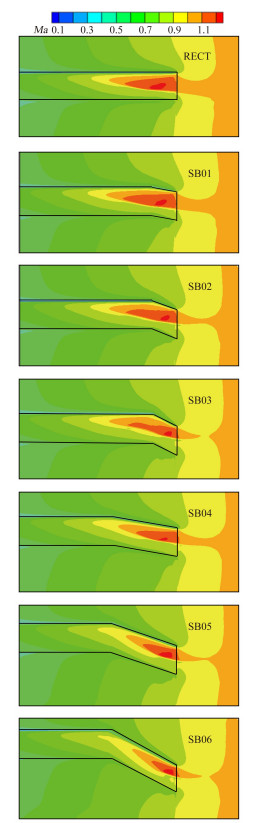
| 图 7 不同后掠桨叶的等马赫数云图 Fig. 7 Contour maps of Mach number distributions of various sweep-back blades |
从图 7中可以看出,随着后掠角的增大,桨叶表面的超声速流动区域对桨叶外部的超声速区域影响越来越小。随着后掠角的增大,桨尖处剖面法向来流速度减小,而展向流速增大,这虽然导致超声速区域中心向桨尖移动,但是超声速流动范围减小。因此随着后掠角的增加,桨叶表面超声速流动区域对空间流动影响减弱,负压峰值逐渐减小。随着后掠位置向桨叶内侧移动,后掠范围不断扩大,超声速流动范围减小,导致桨叶表面激波对空间流动区域的影响随着后掠范围的扩大而减小,因此负压峰值也随之减小。比较SB03和SB06桨叶发现,桨叶表面的激波均未扩展至外部超声速流动区域,没有发生严重的离域化现象。
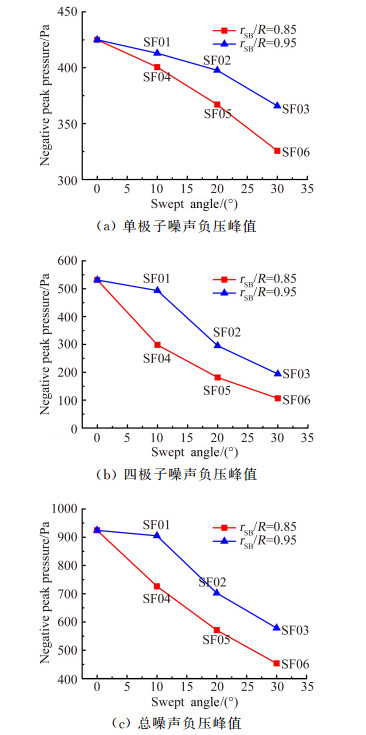
3.2 桨尖前掠的参数影响分析图 8(a)、(b)和(c)分别给出了不同前掠位置时厚度噪声负压峰值、四极子噪声负压峰值和总噪声负压峰值随后掠角的变化,其中rSF表示后掠起始位置。观察图 8(a)、(b)和(c)发现,总噪声负压峰值的变化趋势和四极子噪声负压峰值的变化趋势一致,前掠桨叶对单极子声源项引起的厚度噪声影响不大。厚度噪声大小随前掠位置和前掠角度的变化总体上是单调变化的,厚度噪声负压峰值随前掠角增大而减小,随前掠范围的增大而减小。从图 8(b)和(c)中可以看出,前掠位置固定时,负压峰值总体上随着前掠角的增大而较小;前掠角固定时,负压峰值总体上随着前掠位置靠桨叶内侧而减小。观察SF01桨叶可以发现,它的四极子噪声负压峰值、厚度噪声负压峰值和矩形桨叶接近,结果导致总噪声负压峰值接近矩形桨叶的负压峰值,同样发生了严重的离域化现象。
|
| 图 8 不同前掠桨尖旋翼的噪声负压峰值比较 Fig. 8 Comparisons of negative peak pressure of rotors with various sweep-forward blades |
图 9给出了不同外形参数的后掠桨叶等马赫数分布云图。SF01的等马赫数线云图和矩形桨叶相似,这也可以是图 8(b)中SF01桨叶的四极子噪声负压峰值和矩形桨叶接近的原因。而SF03、SF05和SF06桨叶中桨叶表面激波对半径之外的空间区域影响最弱,这也可以解释图 8(b)中SF03、SF05和SF06桨叶四极子噪声负压峰值最小的现象。从图 9中可以看出,随着前掠角的增大,桨叶表面的超声速流动区域对桨叶外部的超声速区域影响越来越弱。随着前掠角的增大,桨尖处剖面法向来流速度减小,而展向流速增大,这导致超声速区域中心向桨叶内侧移动,并且桨叶表面超声速流动范围减小,激波的强度也随之减弱。因此随着前掠角的增加,桨叶表面超声速流动区域对空间影响减弱,负压峰值逐渐减小。随着前掠位置向桨叶内侧移动,前掠范围扩大,桨叶表面超声速流动区域位置虽然改变不大,但是范围逐渐减小,激波强度也随之减小。因此随着前掠范围的扩大,桨叶表面超声速流动区域对空间影响减弱,负压峰值逐渐减小。而比较SF03、SF05和SF06桨叶发现,桨叶表面的超声速流动区域均未影响到外部超声速区域,激波未扩展至空间区域,没有发生严重的离域化现象,相比于矩形桨叶,SF06的四极子噪声负压峰值降低幅度达80%。

|
| 图 9 不同前掠桨叶的等马赫数云图 Fig. 9 Contour maps of Mach number distributions of various sweep-forward blades |
相同变掠角度和相同变掠位置的后掠桨叶和前掠桨叶相比,前掠桨叶能够更加有效地降低旋翼HSI噪声。这是因为虽然前掠和后掠均能够减小剖面法向来流、增加展向入流,从而减弱桨叶表面超声速流动范围以及减弱激波强度,但是后掠桨叶驱使超声速流动区域向桨尖移动,有可能影响到桨尖之外的超声速区域,从而引起离域化现象。相反,前掠桨叶不仅减弱了桨叶表面超声速流范围,而且驱使超声速流动区域向桨叶内侧移动,减小了其对桨尖之外超声速区域的影响,有效地防止了激波扩展至外部空间流动区域。
4 结论1) 建立的CFD/FW-H_pds方法可以有效地预测旋翼跨声速状态下的噪声辐射特性;
2) 高桨尖马赫数时桨叶表面激波扩散至桨尖外部的超声速区域是旋翼跨声速离域化现象的产生原因。随着桨尖马赫数的增加,旋翼高速脉冲噪声辐射愈加强烈,离域化现象愈加明显,声压波形呈现一定的非对称性;
3) 后掠桨尖和前掠桨尖对抑制旋翼跨声速特性有不同效果。后掠桨尖和前掠桨尖均能够减小桨叶表面超声速流动范围,降低激波强度,减小对桨尖外部的超声速区域的影响,避免发生离域化现象,从而降低四极子噪声。另外,前掠桨叶能够驱使超声速流动区域向桨叶内侧移动,进一步降低了激波扩展至外部超声速区域的可能性,从而能够更好地降低旋翼高速脉冲噪声。
| [1] | Boxwell D A, Yu Y H, Schmitz F H. Hovering impulsive noise-some measured and calculated results[J]. Vertica, 1979, 3(1):35–45. |
| [2] | Yang C, Aoyama T, Chae S. Blade planform optimization to reduce HSI noise of helicopter in hover[C]//Proceedings of the 64th Annual Forum of the American Helicopter Society, Montreal:American Helicopter Society, 2008:2218-2232. |
| [3] | Isom M P. Acoustic shock waves generated by a transonic helicopter blade[C]//Proceedings of the 36th Annual Forum of the American Helicopter Society, New York:American Helicopter Society, 1980:063(1)-063(18). |
| [4] | Schmitz F H, Yu Y H. Transonic rotor noise-theoretical and experimental comparisons[J]. Vertica, 1981, 5:55–74. |
| [5] | Hawkings D L, Lowson M V. Theory of open supersonic rotor noise[J]. Journal of Sound and Vibration, 1974, 36(1):1–20. DOI:10.1016/S0022-460X(74)80340-8 |
| [6] | Shenoy K R. Asemiempirical high-speed rotor noise prediction technique[J]. Journal of the American Helicopter Society, 1984, 29(1):34–39. |
| [7] | Williams J E F, Hawkings D L. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society A Mathematical and Physical Sciences, 1969, 264(1151):321–342. DOI:10.1098/rsta.1969.0031 |
| [8] | Brentner K S, Farassat F. Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces[J]. AIAA Journal, 1998, 36(8):1379–1386. DOI:10.2514/2.558 |
| [9] | Di Francescantonio P. A new boundary integral formulation for the prediction of sound radiation[J]. Journal of Sound and Vibration, 1997, 202(4):491–509. DOI:10.1006/jsvi.1996.0843 |
| [10] |
Han Z H, Song W P, Qiao Z D. Comparison of time domain prediction methods for transonic aeroacoustic noise generated by helicopter rotors[J].
Acta Aeronautica et Astronautica Sinica, 2006, 27(5):756–762.
(in Chinese) 韩忠华, 宋文萍, 乔志德. 应用于跨声速旋翼气动声学计算的两种时域方法的比较[J]. 航空学报, 2006, 27(5) : 756–762. |
| [11] | Johnson C S, Barakos G N. Optimizing rotor blades with approximate british experimental rotor programme tips[J]. Journal of Aircraft, 2014, 51(2):447–463. DOI:10.2514/1.C032042 |
| [12] |
Song W P, Han Z H, Wang L Q. The effect of blade-tip shape on rotor aeroacoustic noise by Euler/Kirchhoff method[J].
Chinese Journal of Computational Physics, 2001, 18(6):569–572.
(in Chinese) 宋文萍, 韩忠华, 王立群. 旋翼桨尖几何形状对旋翼气动噪声影响的定量计算分析[J]. 计算物理, 2001, 18(6) : 569–572. |
| [13] |
Wang L Q, Song W P. Investigation of helicopter rotor aeroacoustics for different tip shapes[J].
Acta Aeronautica et Astronautica Sinica, 2000, 21(1):48–51.
(in Chinese) 王立群, 宋文萍. 旋翼桨尖形状对噪声影响量级的研究[J]. 航空学报, 2000, 21(1) : 48–51. |
| [14] |
Wang B, Zhao Q J, Fan F. Investigations on acoustic characteristics of rotor with improved CLOR blade-tip in hover based on experimental and prediction method[J].
Acta Aerodynamica Sinica, 2013, 31(4):454–461.
(in Chinese) 王博, 招启军, 樊枫. 改进型CLOR桨尖旋翼悬停状态气动噪声特性试验与预估分析[J]. 空气动力学学报, 2013, 31(4) : 454–461. |
| [15] | Zhao Q J, Xu G H. Astudy on aerodynamic and acoustic characteristics of advanced tip-shape rotors[J]. Journal of American Helicopter Society, 2007, 52(3):201–213. DOI:10.4050/JAHS.52.201 |
| [16] |
Wang B, Zhao Q J, Xu G. A new moving-embedded grid method for numerical simulation of unsteady flow-field of the helicopter rotor in forward flight[J].
Acta Aerodynamica Sinica, 2012, 30(1):14–21.
(in Chinese) 王博, 招启军, 徐广. 一种适合于旋翼前飞非定常流场计算的新型运动嵌套网格方法[J]. 空气动力学学报, 2012, 30(1) : 14–21. |
| [17] | Zhao Q J, Xu G H, Zhao J G. Numerical simulations of the unsteady flowfield of helicopter rotors on moving embedded grids[J]. Aerospace Science and Technology, 2005, 9(2):117–124. DOI:10.1016/j.ast.2004.10.004 |
| [18] | Lomax H, Baldwin B S. Thin layer approximation and algebraic model for separated turbulent flows[R]. AIAA-78-257, 1978. |
| [19] | Harten A, Hyman J M. Self adjusting grid methods for one-dimensional hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 50(2):235–269. DOI:10.1016/0021-9991(83)90066-9 |
| [20] | Abhishek A, Data A, Chopra I. Prediction of UH-60A structural loads using multibody analysis and swashplate dynamics[J]. Journal of Aircraft, 2009, 46(2):474–490. DOI:10.2514/1.35076 |
| [21] | Baeder J D, Gallman J M, Yu Y H. A computational study of the aeroacoustics of rotors in hover[J]. Journal of the American Helicopter Society, 1997, 42(1):39–53. DOI:10.4050/JAHS.42.39 |



