2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Institute of Computational Aerodynamics of China Aerodynamics Research and Development Center, Mianyang 621000, China
自然界的鸟类经过亿万年的进化,形成了出色的飞行能力,其飞行效率、机动性都远远超出了目前所有的人造飞行器。具有较低能耗、噪声,同时具有优越机动性能的小型扑翼飞行器是未来航空器发展的一个重要方向,为开展此类研制工作,首先需要对鸟类扑翼运动过程中的升力、推力产生机制以及流动控制机理进行深入细致的研究。
鸟类翅膀的构造非常精细,由肌肉、骨骼、羽毛和多个关节组成,扑翼过程中伴随着翅膀的弦向转动、展向的收缩-伸展以及扭转[1],其飞羽在上拍、下拍过程也会规律性的收缩-合拢。鸟类的升力主要源于翼型本身以及翼型的非对称拍动,例如海鸥的翼型剖面和S1223翼型非常相似,在低速情况下具有很高的升阻比,而鸟翼在下拍过程中会完全打开,上拍过程中则会尽量收缩,且其上拍、下拍的时间也存在很大差异,这种非对称拍动的目的也是为了增强升力。
目前国内外常见的关于鸟类扑翼飞行的研究工作大概可以分为两类:一类通过观测,采用数据统计和量纲分析的手段,分析鸟类形态和各飞行参数之间的关系,并得到一些经验性的公式,如Greenewalt[2]、Tennekes[3]、Pennycuick[4]等人的工作。另一类则是采用试验、理论或近似的数值分析方法,针对具体的扑翼过程开展研究,如Jones[5]、Angela[6]、Pennycuick[7]、Rayner[8]、Phlips[9]等人的工作。其中“面元法”作为一种简单有效的数值模拟手段,在鸟类扑翼的研究中使用较多,如Smith[10]采用该方法并结合有限元模型对柔性扑翼运动进行了研究,国内的昂海松研究团队[11]、余永亮[12]等也分别采用该方法对昆虫及蝙蝠的扑翼进行了研究。
虽然这些针对鸟类扑翼运动的研究已经初步揭示了鸟类的升力、推力产生机制,然而这些定性的认识仍不能满足扑翼飞行器设计上的需求。鸟类扑翼运动的许多细节问题如翼型、迎角、展向变形/扭转、上/下拍动时间比、拍动频率等对其力学特性有非常重要的影响,因此非常有必要针对这些细节问题进行深入研究。
计算流体力学的迅速发展为扑翼运动的精细化研究提供了条件,且已经在昆虫的扑翼研究中得到了广泛应用[13-16]。然而由于鸟类扑翼过程的复杂性,三维情况下复杂扑翼过程的精细化数值研究还不多见,很多数值研究工作仍基于二维或者简单的三维扑翼开展[17-18]。
本文以海鸥的扑翼飞行为研究背景,选择二维的S1223翼型作为研究对象,采用动态混合网格技术及非定常数值模拟方法,对其刚性俯仰-沉浮运动进行了研究,得到了下拍时间比、拍动迎角等参数的影响规律。这些工作为后续的复杂三维问题的数值研究奠定了基础。
1 数值计算方法本文的数值模拟基于HyperFLOW软件平台[19]开展。该软件平台是中国空气动力研究与发展中心研发的具有完全自主知识产权的大型CFD多学科通用求解平台,具有优越的体系架构和生态系统,并已集成了结构/非结构NS方程流场解算器、动态混合网格生成技术、飞行力学/流体动力学一体化算法等,可进行完全气体和化学非平衡气体的定常/非定常计算。以下对其中的动态混合网格技术以及非定常算法进行简要介绍。
1.1 动态混合网格生成技术常用的网格变形技术有弹簧松弛法、求解偏微分方程的方法以及插值方法等。在之前的研究工作中,作者所在的课题组建立了弹簧松弛法和插值法相结合的混合网格变形技术,具有较好的变形能力和动网格生成效率,并通过结合局部网格重构技术,提高了针对大变形、大位移、相对运动等复杂动边界问题的适应能力[20-22]。
在最近的研究工作中,我们进一步发展了基于径向基函数(RBF) 的网格变形技术,该技术具有优越的网格变形能力,是目前国内外CFD工作者争相研究的一个热点。而标准的RBF方法在处理大规模网格时效率极差,为了提高RBF网格变形技术的适用性,我们参考文献[23]的做法,通过选择有限的参考点来减少RBF算法中矩阵的规模,以提高计算效率。
1.2 非定常数值模拟方法基于动态混合网格的NS方程解算器采用了格心型的有限体积格式,时间离散采用二阶的欧拉后插方法,为提高非定常计算效率,采用了双时间步算法和BLU-SGS隐式计算方法。算法具体细节请参见文献[22]。
动网格下的NS方程离散算法必须满足几何守恒律。运动网格下的几何守恒律(GCL) 特指体积守恒,对于控制方程,假设流场均匀,则可得到GCL方程如下:

|
(1) |
其中V为控制体Ω的体积,∂Ω为控制体边界,w表示控制体外边界的运动速度,n为控制体边界的外法向。导数符号“d”表示跟随控制体的随体导数,而不是跟随流体的物质导数。
式(1) 表示控制体单元的体积变化率等于边界面法向运动速度的面积分,其在微分意义下是恒成立的,而计算所采用的离散格式也需要使式(1) 得到满足,才不至于在流场内引入额外的误差。
满足式(1) 的数值格式很多,详见Farhat[24]、Kallinderis[25]、刘君[26]、Wang[27]等的工作。这里我们采用了一种较为便捷的方法:直接对边界面的法向速度进行约束。以一阶欧拉隐式方法为例,式(1) 的离散形式为:
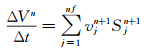
|
(2) |
式中v=w · n表示控制体边界面的法向速度。对于单元的每一个离散的边界面,限定其法向速度的求解方法:
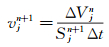
|
(3) |
其中ΔVjn表示单元第j个面扫过的面积。则式(3) 是满足式(2) 的充分条件。同理,对于二阶欧拉隐式格式,应当选用如下的法向速度求解方法:
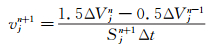
|
(4) |
在随后的研究中,我们进一步从误差分析的角度对各种运动网格几何守恒算法进行了理论分析,发现可以将现有的几何守恒算法归为两类,即限制整体积分误差的“体限制方法”和限制每个边数值误差的“面限制方法”,并分别可以针对不同的时间格式写成统一的形式。进一步的对比发现,各种几何守恒算法的计算结果大体一致,但是我们发展的几何守恒算法在三维情况下更为简便。具体的理论分析详见文献[28]。
2 翼型及俯仰-沉浮运动根据文献描述[29],本文选用二维S1223翼型作为研究对象,翼型弦长c=0.2m。将整个拍动周期分为下拍和上拍两个阶段,其沉浮运动规律如下:
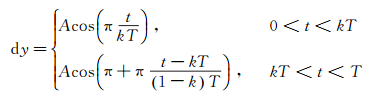
|
(5) |
其中dy为翼型的纵向位移,A为振幅,T为拍动周期,k表示下拍时间和整个拍动周期T的比值。本文令振幅A=0.2m。
翼型绕其1/4弦长处进行俯仰,俯仰角(低头为正) 变化规律如下:
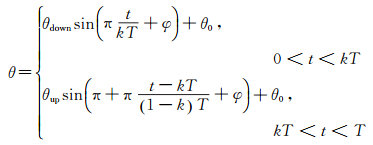
|
(6) |
其中θ0表示上拍和下拍过程的起始拍动角,φ表示俯仰角变化与上拍-下拍运动之间的相位差。本文令φ=0、θ0=0,因此俯仰角振幅θdown、θup分别代表最大下拍角和最大上拍角,且最大拍动角出现在上拍或下拍过程的中间时刻。
本文只针对二维问题进行数值模拟,其相当于三维问题的一个展向截面(如图 1所示)。

|
| 图 1 翼型的俯仰-沉浮运动示意图 Fig. 1 Sketch of 2D plunging/flapping motion of the airfoil |
取来流速度U=10m/s,翼型拍动频率
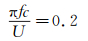
|
(7) |
本文需要研究俯仰-沉浮运动的能耗特性,能耗系数CP的定义如下:

|
(8) |
其中f表示流体作用在物体边界上的力,w表示边界元的运动速度,∂Ω表示物体表面。
3 数值结果分析采用混合网格离散计算域,物面附近采用各向异性的四边形单元。翼型外围采用三角形网格单元,并在翼面附近以及尾迹内进行了加密处理,网格单元总数8.6万(图 2)。计算采用SA湍流模型,不考虑转捩因素的影响,采用二阶空间和时间格式,一个拍动周期采用400个非定常时间步离散。
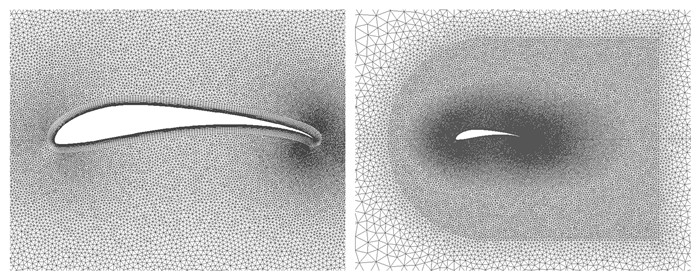
|
| 图 2 S1223翼型及计算网格 Fig. 2 S1223 wing and computational mesh |
3.1 下拍时间比对升力及能耗的影响
观察发现[30],海鸥等鸟类巡航飞行时其下拍时间占到整个拍动周期的60%~80%,说明下拍时间比k与其力学特性关系密切。本节不考虑翼型的俯仰,仅考虑其上下沉浮运动,针对k=0.40~0.75等几种情况进行数值模拟。
图 3(a)所示为不同k值情况下升力系数在一个周期内的变化曲线,横坐标为拍动的相位角。下拍过程中(Phase < π),在翼型的随体坐标系下来流的等效迎角为正,因此产生正升力,但是随着k值的增加,翼型下拍的速度减小,等效迎角减小,因此升力峰也随之减弱;上拍过程中,翼型等效迎角为负,因此翼型产生负升力,且随着k的增加,上拍速度增加,负升力峰增大。但是由于翼型本身具有较好的升阻比特性,在上拍和下拍的起始阶段(Phase=0、π附近) 仍然可以维持较大的升力系数,这对于增大整个拍动周期的平均升力是有益的。俯仰运动的瞬时能耗系数与翼型拍动速度的大小关系密切,在拍动速度最快的时刻(Phase=0.5π、1.5π) 会出现能耗的峰值(如图 3b所示),随着k值的增加,下拍过程的能耗峰值减弱,而上拍过程能耗峰值则会增加。
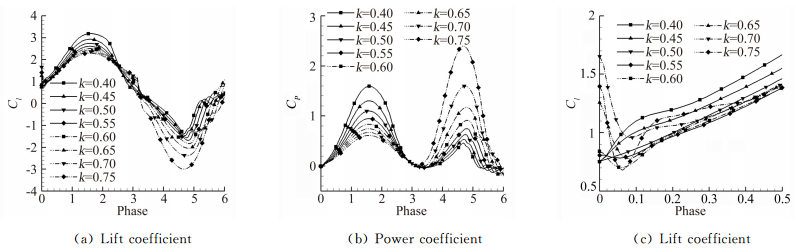
|
| 图 3 不同k值下一个拍动周期内的气动力系数 Fig. 3 Aerodynamic coefficients in a period at different value of k |
图 4所示为拍动一个周期内几个典型相位的涡量云图,在Phase=0.5π、1.5π两个相位下,不同的k值对应的流场结构基本类似,只是由于k值的变化影响了其下拍和上拍过程的等效迎角,因此背风区内的旋涡大小、形态等存在一些差异;而Phase=0、π两个相位下,翼型的法向运动速度为0,但是加速度处在整个拍动周期的峰值,此时不同k值条件下流场的旋涡结构存在较大差异。以Phase=0为例,此时处于上拍结束的急剧减速以及下拍起始的急剧加速阶段,翼型带动周围流体急剧加速/减速,受“附加质量效应”影响较大,且由于本文设计的运动规律在此时的加速度不连续,因此导致升力系数存在“不规律”的波动(图 3c)。然而,由于翼型拍动的减缩频率较小,来流速度相对于拍动速度是一个较大的量,因此这些“不规则”的旋涡结构会很快消失在尾迹,升力系数也会很快进入单调增加的趋势。
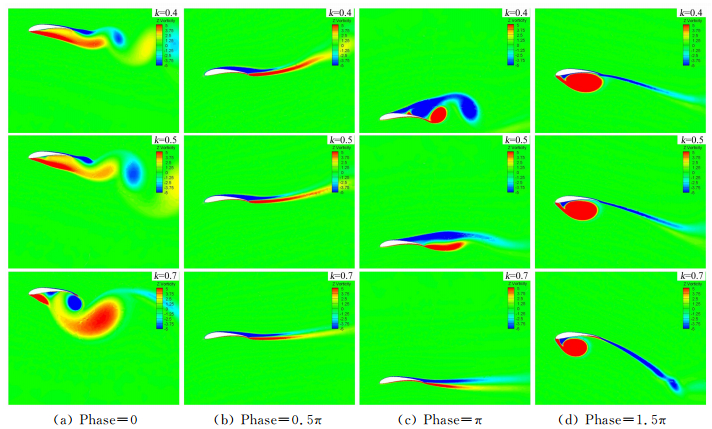
|
| 图 4 典型相位下的涡量云图(从上至下的依次为:k=0.4、0.5、0.7) Fig. 4 Vorticity contours at four typical phase angles (from upper to lower:k=0.4、0.5、0.7) |
上述的数值模拟结果表明,翼型的下拍过程对升力的贡献较大,而上拍过程则产生负升力。实际上,鸟类在扑翼过程中正是通过翅膀展向的折转来突出下拍的“有益”作用(下拍时翼面全部展开、增大有效升力面),减弱上拍的“不利”影响(上拍时适当折叠扑翼,减小上拍迎风阻力面)。为了近似反应这种“三维效应”,本文对升力、阻力、能耗等引入一个近似的加权系数:

|
(9) |
λ在0.5和1.0之间周期性变化,φ表示加权系数和扑翼运动之间的相位差,本文令φ=0。将计算得到的瞬时气动力系数乘上加权系数λ,则本文的二维问题可近似看作一个三维的翼型在做俯仰-沉浮运动的同时改变其展向长度。
考虑加权前后,扑翼运动的时均升力系数、时均能耗系数以及它们之间的比值随k值的变化如图 5所示:与原始模式(Original Mode) 相比,加权模式(Weighted Mode) 下时均升力系数整体上有所增加,时均能耗系数则在整体上有明显的降低。加权模式下,随着k的增加,升力系数呈增加的趋势,而时均升力/能耗比先增加后减少,并在k=0.65~0.7附近出现最大值。这个结论和自然界一些鸟类的观测数据保持一致[29-30]。
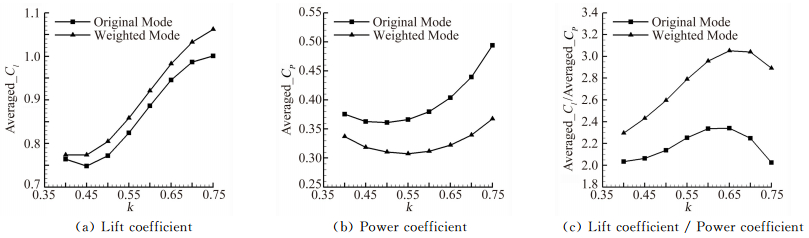
|
| 图 5 时均气动力参数随k值的变化 Fig. 5 Time-averaged aerodynamic coefficients for original mode and weighted mode |
3.2 拍动角的影响
本节取k=0.7,令θdown=θup,分别针对-5°~45°等若干拍动角的情况进行了数值模拟,分析拍动角对扑翼过程气动力特性的影响。
一个拍动周期内升力系数、阻力系数的变化情况如图 6所示,图中横坐标为扑翼运动的相位。分别针对下拍过程和上拍过程进行单独分析。下拍过程中(Phase=0~π),随着拍动角θdown的增加,相对于翼型而言来流迎角减小,因此升力系数的峰值减弱,且当θdown>25°时甚至会出现负的升力峰;就阻力系数而言,在一定的θdown范围内为负值,说明产生了“推力”作用,但是随着θdown的增加,“推力”的峰值逐渐减小,并最终导致阻力的产生。在上拍过程中(Phase=π~2π),相对于翼型而言来流的等效迎角为负,因此当上拍角θup较小时,会出现负的升力峰值,但是随着θup的增加,负升力峰逐渐减弱,并在一定条件下变为正值。

|
| 图 6 不同拍动角时一个周期内的瞬时气动力系数 Fig. 6 Lift coefficients and power coefficients in a period for different maximum flapping angles |
采用和3.1节相同的方法,为升力、阻力系数引入公式(9) 所示的加权系数λ,得到拍动过程的时均力学系数如图 7所示,图中横坐标为最大拍动角。下拍过程的时均升力系数在θdown=-2°时出现最大值,之后随着θdown的增加而单调减小,在θdown=30°左右变为负值;时均阻力系数的最小值出现在θdown=0°附近,之后随着θdown的增加而单调增加,在θdown=21°左右变为正值。上拍过程的时均升力系数随上拍角的增加而单调增加,并在θup=25°附近变为正值,说明上拍过程仍可能产生升力;就阻力而言,在各个θup条件下其时均值均为正,只是在一定的条件下具有较小的量,从图 7可以确定出这个阻力最小的拍动角约为θup=20°。
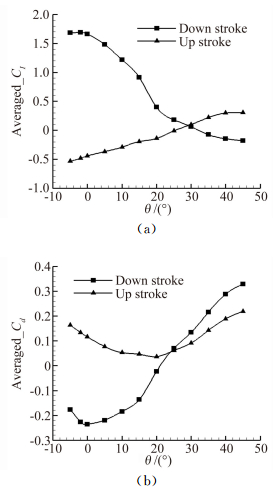
|
| 图 7 时均升力、时均阻力随最大拍动角θ的变化 Fig. 7 Time-averaged lift and drag coefficients for different maximum flapping angles |
这些数值结果表明,翼型的拍动角度对其升阻力特性影响极大,因此采用合适的拍动角是其提高升力、增加推力的关键。下拍过程对升力、推力的产生都是有利的,且θdown=0°时具有较好的升阻力特性。由于本文所采用模型的局限性,在各个上拍角条件下,上拍过程中均无法产生推力,但是在合适的角度下能够保证较小的阻力,且当上拍角大于一定数值时仍能够产生升力。
3.3 优化的拍动方式根据3.2节的分析,选择θdown=0°,针对θup=20°的情况进行了数值模拟。
拍动一周期内升力系数、阻力系数的变化曲线如图 8所示,横坐标表示拍动的相位。拍动过程中几个典型状态下的瞬时流线及压力云图如图 9所示(为体现来流的“等效迎角”,速度场减去了翼型在y方向运动速度)。

|
| 图 8 优化拍动角情况下一周期内的气动力系数 Fig. 8 Aerodynamic coefficients in a period at the optimal flapping angle |
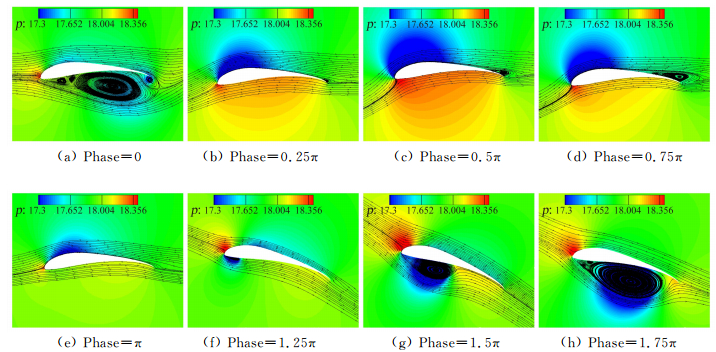
|
| 图 9 拍动过程中几个典型时刻的瞬时流线及压力云图 Fig. 9 Streamlines and pressure contours at some typical times |
下拍过程中(Phase=0~π),翼型背风区内的流动分离较弱,仅在个别时刻在尾缘附近出现了较小的流动分离,因此整个下拍过程中翼型的升力系数均为正,且存在较大的升力峰值。从压力云图也可以看出,下拍过程中在翼型头部存在较强的负压区,可诱导出较大的升力以及正推力。
上拍过程的起始及结束阶段,翼型的升力系数仍为正值,仅在下拍过程的中间阶段出现负升力。这是由于上拍过程中翼型存在较大的上拍角度,相对于来流,翼型的等效“负”迎角减小,因此上拍的不利影响会得到减弱。
下拍-上拍的转换阶段(Phase=0、π),由于本文所采用的运动规律在此时的俯仰角速度不连续,导致力学系数出现跳跃,但是这些瞬时的强非定常现象对整个拍动周期的影响相对较弱。
采用与3.1节相同的做法,引入公式(9) 所示的加权系数,将力学系数进行加权,得到的整个拍动过程的时均升力系数、阻力系数和能耗系数分别为1.10、-0.14、0.24。定义效率:

|
(10) |
则扑翼的推进效率约为58.3%。
4 结论本文以海鸥等大型鸟类的巡航飞行状态为研究背景,选择S1223翼型以及相应的扑翼运动参数作为研究对象,希望通过这些初步的研究,探讨翼型俯仰-沉浮运动过程的升力、推力的产生机理。
本文选用的扑翼方式具有较小的减缩频率,和昆虫等的扑翼方式不同,其非定常效应较弱,翼型的静态因素对气动力特性影响则较大。翼型通过沉浮运动改变来流的相对迎角,在下拍过程中,来流等效迎角为正,且由于非定常流动的迟滞作用,翼型背风区内的流动分离现象很弱,鉴于S1223翼型优秀的升阻比特性,气动力合力指向翼型前上方,同时产生“升力”和“推力”(图 10所示)。
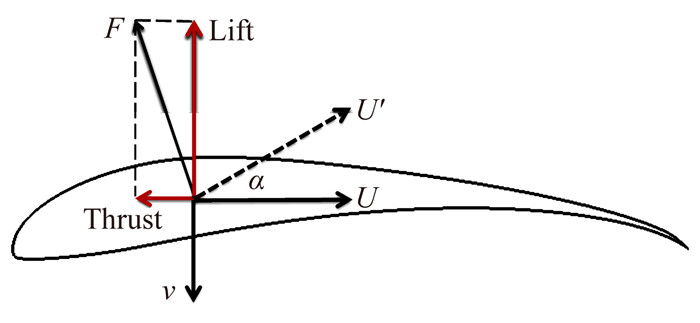
|
| 图 10 翼型下拍过程中的气动力分解 Fig. 10 The components of aerodynamic force during the down-stroke process |
文献[18]的数值模拟结果表明,三维柔性翼型在上拍过程仍有较大的推力产生。而在本文所选用的模型及运动方式条件下,上拍过程没有能够产生推力,其原因可能在于:(1) 本文选用的翼型在负迎角条件下具有较差的力学特性;(2) 本文采用刚性的俯仰-沉浮运动方式,没有考虑到实际情况下翼型的柔性变形;(3) 所选用的扑翼运动参数如频率、拍动角等存在差异。
下拍时间、拍动角等扑翼参数对翼型的气动力特性影响较大。在本文的数值模拟条件下,当下拍时间占整个拍动周期的65~70%左右时具有较好的时均升力/能耗比,而下拍角取为0°,上拍角取为20°时具有较好的升力、推力产生性能。
本文仅针对刚性的二维扑翼模型进行了数值模拟,初步分析了下拍时间、拍动角等的影响,对其推力、升力产生机理有了定性的认识。而三维情况下的扑翼运动具有更多的自由度,并且存在柔性变形如翼沿展向的弯曲、扭转等。这些三维效应对升力、推力的影响很大,下一步我们将重点开展这方面的研究工作。
| [1] | Brown R H J. The flight of birds[J]. Journal of Experimental Biology, 1952, 25:90–103. |
| [2] | Greenewalt C H. Dimensional relationships for flying animals[J]. Smithson. Misc. Collect, 1962, 144:1–46. |
| [3] | Tennekes H. The simple science offlight:from insects to jumbo jets[M]. Boston, MA: MIT Press, 1996. |
| [4] | Pennycuick C J. Speeds and wing-beat frequencies of migration birds compared with calculated benchmarks[J]. J. Exp. Biol., 2001, 204:3283–3294. |
| [5] | Jones K D, Center K B. Wake structures behind plunging airfoils:a comparison of numerical and experimental results[R]. AIAA paper, 96-0078, 1996. |
| [6] | Angela M B, Andrew A B. Wing and body kinetics of takeoff and landing flight in the pigeon[J]. J. Exp. Biol., 2010, 213:1651–1658. DOI:10.1242/jeb.038109 |
| [7] | Pennycuick C J. Power requirements for horizontal flight in the pigeon[J]. J. Exp. Biol., 1968, 49:527–555. |
| [8] | Rayner J M V. A new approach to animal flight mechanics[J]. J. Exp. Biol., 1979, 80:17–54. |
| [9] | Phlips P J, East R A, Pratt N H. An unsteady lifting line theory of flapping wings with application to the forward flight of birds[J]. J. Fluid Mech., 1981, 112:97–125. DOI:10.1017/S0022112081000311 |
| [10] | Smith M J C. Simulating moth wing aerodynamics:Towards the development of flapping-wing technology[J]. AIAA J, 1996, 34:1348–1355. DOI:10.2514/3.13239 |
| [11] |
Zeng R. Aerodynamic characteristics of flapping-wing MAV simulating bird flight[D]. Nanjing University of Aeronautics and Astronautics, 2004(in Chinese). 曾锐.仿鸟微型扑翼飞行器的气动特性研究[D].南京航空航天大学博士学位论文, 2004. |
| [12] |
Yu Y L. A theoretical modeling study on unsteady aerodynamics of wing flapping during insect forward flight[D]. University of Science and Technology of China, 2004(in Chinese). 余永亮.昆虫前飞拍翼非定常空气动力学的理论模化研究[D].中国科学技术大学博士学位论文, 2004. |
| [13] | Ito Y, Nakahashi K. Flow simulation of flapping wings of an insect using overset unstructured grid[R]. AIAA paper, 2001-2619. |
| [14] | Miller L A, Peskin C S. When vortices stick:an aerodynamic transition in tiny insect flight[J]. J. Exp. Biol., 2004, 207:3073–3088. DOI:10.1242/jeb.01138 |
| [15] | Liu H, Ellingtona C P. Computational fluid dynamic study of hawkmoth hovering[J]. J. Exp. Biol., 1998, 201:461–477. |
| [16] | Liang B, Sun M. Aerodynamic interactions between contralateral wings and between wings and body of a model insect at hovering and small speed motions[J]. Chinese Journal of Aeronautics, 2011, 24(4):396–409. DOI:10.1016/S1000-9361(11)60047-2 |
| [17] | Ashraf M A, Young J, Lai J C S. Reynolds number, thickness and camber effects on flapping airfoil propulsion[J]. Journal of Fluids and Structures, 2011, 27:145–160. DOI:10.1016/j.jfluidstructs.2010.11.010 |
| [18] | Unger R, Haupt M C, Horst P, et al. Fluid-structure analysis of a flexible flapping airfoil at low Reynolds number flow[J]. Journal of Fluids and Structures, 2012, 28:72–88. DOI:10.1016/j.jfluidstructs.2011.08.009 |
| [19] | He X, Zhang L P, Zhao Z. The research and development of structured-unstructured hybrid CFD software[C]//The ninth Asian CFD conference, Nanjing, 2012. |
| [20] |
Zhang L P, Duan X P, Chang X H, et al. A hybrid dynamic grid generation technique for morphing bodies based on Delaunay graph and local remeshing[J].
ATCA Aerodynamica Sinica, 2009, 27(1):26–32.
(in Chinese) 张来平, 段旭鹏, 常兴华, 等. 基于Delaunay背景网格插值方法和局部网格重构的动态混合网格生成技术[J]. 空气动力学学报, 2009, 27(1) : 26–32. |
| [21] | Zhang L P, Chang X H, Duan X P, et al. Applications of dynamic hybrid grid method for three-dimensional moving/deforming boundary problems[J]. Computers & Fluids, 2012, 62:45–63. |
| [22] | Zhang L P, Wang Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers & Fluids, 2004, 33:891–916. |
| [23] | Rendall T C S, Allen C B. Reduced surface point selection options for efficient mesh deformation using radial basis functions[J]. Journal of Computational Physics, 2010, 229:2810–2820. DOI:10.1016/j.jcp.2009.12.006 |
| [24] | Lesoinne M, Farhat C. Geometric conservation laws for flow problems with moving boundaries and deformable meshes, and their impact on aero-elastic computations[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 134:71–90. DOI:10.1016/0045-7825(96)01028-6 |
| [25] | Ahn H T, Kallinderis Y. Strongly coupled flow/structure interactions with a geometrically conservative ALE scheme on general hybrid meshes[J]. Journal of Computational Physics, 2006, 219:671–696. DOI:10.1016/j.jcp.2006.04.011 |
| [26] |
Liu J, Bai X Z, Zhang H X, et al. Discussion about GCL for deforming grids[J].
Aeronautical Computing Technique, 2009, 39(4):1–5.
(in Chinese) 刘君, 白晓征, 张涵信, 等. 关于变形网格"几何守恒律"概念的讨论[J]. 航空计算技术, 2009, 39(4) : 1–5. |
| [27] | Wang Z J, Yang H Q. Unsteady flow simulation using a zonal multi-grid approach with moving boundaries[R]. AIAA Paper, 1994-0057. |
| [28] | Chang X H, Ma R, Zhang L P, et al. Further study on the geometric conservation law for finite volume method on dynamic unstructured mesh[J]. Computers & Fluids, 2015, 120(5):98–110. |
| [29] | Liu T S. Avian wing geometry and kinematics[J]. AIAA J., 2006, 44:954–963. DOI:10.2514/1.16224 |
| [30] | McCroskey W J, McAlister K W. Dynamic stall on advanced airfoil sections[J]. Journal of the American Helicoper Society, 1981, 26(3):40–50. DOI:10.4050/JAHS.26.40 |



