2. 中国空气动力研究与发展中心 超高速空气动力研究所, 四川 绵阳 621000
2. Hypervelocity Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
随着载人航天的深化发展、探月工程的逐步推进和深空探测的日臻实践,航天器再入速度持续增大,烧蚀、通信黑障等超高速典型现象愈加显著,为其气动力/热和等离子体特性预测提出了严峻挑战。神舟飞船等近地轨道航天器以第一宇宙速度7.9km/s再入大气层,气体发生强烈的非平衡化学反应和微弱电离,通信黑障主要发生在高空近连续流区域;2014年秋发射并成功返回的探月飞行试验器返回器以11.2km/s的速度蛙跳式再入大气层,非平衡化学反应和电离现象更为严重,通信黑障大幅向稀薄流区延伸;彗星探测器Stardust[1]实现了迄今人造飞行器的最高速度,它以12.8km/s的速度再入大气层,非平衡化学反应和电离极为严重,通信黑障覆盖宽广的稀薄区域。
传统的空气动力学[2]研究重点关注连续流区的气动力/热问题,百余年来极大地促进了航空航天事业的发展。但是,随着稀薄间段粒子效应的增强,连续介质假设失效,理论分析和数值计算难以实现上述极高速再入过程、尤其是稀薄段电离特性的有效预测;同时,受设备能力和测试手段的限制,地面风洞和模型飞行试验也无法完成上述高温高速非平衡条件的真实再现。近年来针对稀薄气体发展的多种方法中,基于Boltzmann方程的物理分析和建模计算[3-4]目前还不能包含电离过程,高超声速低密度风洞虽可以实现稀薄却无法达到真实的高温高速环境,只有基于粒子随机统计模拟的DSMC (Direct Simulation Monte Carlo) 方法[5-9]是目前最有可能从数值上研究解决上述问题的一种手段。
1987年,G.A. Bird[10]首次将其提出的DSMC方法用于稀薄气体的电离模拟,这一工作开创了稀薄气体电离过程DSMC模拟研究的先河。他用41个化学反应处理11组元空气涉及到的电离,奠定了此后稀薄气体电离模拟的基本框架。在这一工作中,基于流场电中性假设,Bird将电子与离子进行强制关联,这一做法避免了精确追踪电子运动的繁琐计算,但是电子运动严格受限的处理在物理上是不真实的。限于当时的计算能力,Bird仅用一维驻点线程序模拟AFE的飞行条件。Carlson和Hassan[11]的工作也是基于一维驻点线流动。由于一维驻点线模拟的本质缺陷,这一方法无法考虑飞行器的几何外形,需要指定边界层的边缘条件。也正是这一缺陷,Bird没有成功实现与试验结果的比较[12]。事实上,激波脱体距离与飞行器的几何外形直接强烈关联,即使所有其它计算参数完全相同,不同几何外形飞行器的流场结果存在显著差异,驻点线上的流动也明显不同,真实计算必须考虑飞行器的几何外形。
近年来,稀薄气体电离过程的二维/轴对称模拟结果陆续发表,但是鲜有三维复杂外形的公开报道。Ozawa[1]采用轴对称的Stardust外形,比较了Stardust极高速再入状态下电离的DSMC和CFD计算结果,发现两种方法差异很大。Boyd[12-13]基于轴对称程序,采用稀有组分追踪算法和电离与离子强制关联的方法模拟分析了RAM-C Ⅱ的再入电离情况。樊菁[14]采用稀有组分分离方法、基于轴对称程序模拟了RAM-C Ⅱ的再入电离过程。Shevyrin[15]不将电子作为一种粒子模拟,而是根据等离子体电中性假设将电子密度等于离子密度之和,在此基础上比较了不同模型对于电离反应的区别,其工作也是基于RAM-C Ⅱ外形。Morsa [16]基于DS2V程序,针对Orin外形,比较了不同化学反应模型涉及电离计算的结果,推荐在防热设计中采用Gupta模型[17]。上述工作均基于二维或者轴对称程序,仅适用于简单轴对称外形。同时,它们均基于电子-离子强制关联假设,而这一假设在高维情况下带来计算量的显著增大。
上述方法的另一个缺陷是化学反应的多温度模型,亦即在不同化学反应的实现过程中使用平动、振动和电子温度等多种温度模态或者它们之间的组合。这一处理在不涉及电离的反应时是可行的,但是由于电子是稀有组分,很多时候一个网格中甚至只有一个或者完全没有电子,电子温度计算必然遭遇强烈的统计涨落。这也是公开报道结果鲜有三维的根本原因,即三维情况每个碰撞网格的模拟分子数目必然受到强烈限制,不可能像二维那样达到数十甚至上百。理想的情况是,对于全部化学反应使用单一温度模型,最好是气体全局温度,这正是本文的工作之一。
从工程角度而言,一个有启发意义的工作来自Boyd[18]。它将电子质量人为增大了三个数量级,把电子当作一种普通分子对待。在这种条件下,电子的热运动速度与其它分子(原子、分子和离子) 不存在量级上的差异,亦即电子将与分子整体上同步运动。同时,由于电离度较低,这一调整不会对流场结构产生明显影响。
基于上述总结和启发,本文尝试拓展传统DSMC方法以处理极高速再入条件下的稀薄气体电离过程,发展适用于复杂外形的三维稀薄气体电离模拟程序,为有效预测复杂外形航天器的稀薄电离特性提供一种可能。
1 稀薄气体电离反应的DSMC方法 1.1 化学反应模型对于一般的二体碰撞化学反应,通常可以写成如下形式:
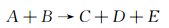
|
(1) |
涉及电离的化学反应包括五种:双原子分子的离解反应、置换反应、联合电离反应及其逆反应、直接碰撞电离反应、离子交换反应。对于离解反应,E代表原子;对于直接电离反应,E代表电子;而对于其它反应,E为空。
化学反应速率常数通常表示为如下Arrhenius形式的方程:
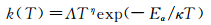
|
(2) |
其中Λ和η为常数,Ea为反应活化能,κ为Boltzmann常数,T为温度。如前所述,不同反应的Τ选取为不同温度模态或者它们的组合,而电子温度计算必然遭遇强烈统计涨落。本文提出:对全部化学和电离反应,采用单一温度模型,即气体当地全局温度。如此,当碰撞总能量Ec>Ea时,上述常数Λ和η通过下式与化学反应概率P相关联:
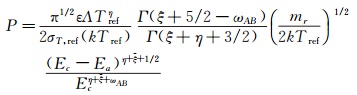
|
(3) |
上式中σT为总截面;ε为对称因子,当A和B相同时,ε取值为2,否则为1;Tref为参考温度;Γ为伽马函数,为平均内自由度,ωAB为黏性指数平均值;mr为约化质量,取值为mr=mAmB/(mA+mB)。
对于空气中的11组元(N2、O2、NO、O、N2+、O2+、NO+、N+、O+和电子e),为对全部化学和电离反应使用单一温度模态并与试验测量值匹配,本文采用Gupta的空气化学反应模型并对涉及电子的反应进行了修正。涉及电子的反应相关常数如下表 1所示,其中Qrea为反应热。
| 编号 | 反应式 | Λ | η | Ea | Qrea |
| 1 | O+N→NO++e | 6.338×10-22 | 0.37 | 4.422×10-19 | -4.422×10-19 |
| 2 | O+O→O2++e | 1.598×10-23 | 0.49 | 1.120×10-19 | -1.120×10-19 |
| 3 | N+N→N2++e | 7.500×10-22 | 0.77 | 9.340×10-19 | -9.340×10-19 |
| 4 | O+e→O++e+e | 8.333×10-14 | 0 | 2.180×10-18 | -2.180×10-18 |
| 5 | N+e→N++e+e | 2.500×10-16 | 0 | 2.330×10-18 | -2.330×10-18 |
| 6 | O2++e→O+O | 9.600×10-11 | -1.51 | 0 | 1.120×10-18 |
| 7 | N2++e→N+N | 2.220×10-11 | -1.23 | 0 | 9.340×10-19 |
| 8 | NO++e→O+N | 1.005×10-10 | 1.63 | 0 | 4.420×10-19 |
1.2 能量分配模型
广泛应用于DSMC方法中描述分子平动能和内能分配的模型是Larsen-Borgnakke (L-B) 模型[5]。在这个模型中,假设转动模式的能谱是连续的,碰撞后分子的能量根据Maxwell平衡态分布函数在平动模式和内能模式之间重新分配。
由于涉及电离的反应包括离解反应、置换反应、联合电离反应及其逆反应、直接碰撞电离反应、离子交换反应等多种类型,有必要对不同类型的碰后内能分配作简单说明。
对于离解反应,以氮气为例:
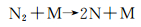
|
(4) |
分解为两个过程:
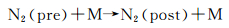
|
(5) |
和
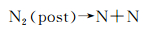
|
(6) |
反应热在式(5) 中予以考虑,同时按照上述L-B能量分配规则将总碰撞能在相对平动能、转动能和振动能之间分配。对于式(6),将N2(post) 的内能转化为两个N原子的相对平动能。
对于直接电离反应,以O为例:
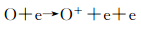
|
(7) |
也类似地分解为两个过程:
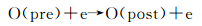
|
(8) |
和
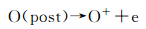
|
(9) |
需要指出的是,式(8) 和式(9) 均不涉及内能的重新分配,因为氧原子和电子均不具备内自由度,将其作为两个步骤处理是便于实施二体碰撞。
联合电离反应是两个原子(不具备内自由度) 生成一个离子(有内自由度) 和一个电子(不具备内自由度),理论上来说可以用L-B方法在生成物之间分配平动能和内能,但是实际操作中可以直接设置离子的转动能和振动能为0,将全部能量指定为相对平动能。联合电离逆反应则有由离子和电子反应生成两个原子,全部碰撞总能量指定为两个原子的相对平动能。
对于置换和离子交换反应,过程较为简单,直接根据L-B方法对生成物进行能量分配即可。
1.3 碰撞分子对抽样方法DSMC方法需要正确确定参与碰撞的分子对数目。在均质气体中,分子之间的碰撞概率与相对速度cr和总碰撞截面σT的乘积成正比。记网格体积为Vc,网格内每个模拟分子代表FN个真实分子,时间步长为Δt。
通常,两种不同方式用于计算网格内的碰撞分子对数。第一种方式是笼统地计算网格内各种组分分子的碰撞对总和,即碰撞分子对数目为:
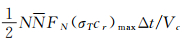
|
(10) |
式中,N为网格中的分子数,是N的均值。对于每一个网格,每一个时间步更新(σTcr)max。由于电子的质量比普通分子小很多,涉及电子碰撞对的σTcr将显著增大,涉及电子的碰撞分子对数目也将显著增大,这在物理上是不真实的。第二种处理方式是在碰撞网格中,考虑两两组分之间的碰撞,亦即组分i和组分j之间的分子碰撞对数为:
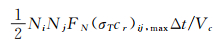
|
(11) |
该方式的最大的问题是Ni和Nj都不会很大而且涨落很大,得到的碰撞分子对数目与真实情况可能差之甚远。
本文采用分组处理的方式:将电子作为一个组P,而将除电子以外的其它组分作为另一个组Q;电子之间没有化学反应发生,同时电子浓度很低,可以不考虑P组内电子的相互碰撞;于是碰撞可以分为两类,即Q组内分子之间的相互碰撞以及P组与Q组分子之间的相互碰撞。同时,统计P组的分子数目NP和Q组的分子数目NQ,于是Q组内的分子碰撞对数为:
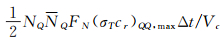
|
(12) |
P组与Q组分子之间的分子碰撞对数为:
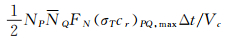
|
(13) |
等离子体效应是稀薄气体电离过程DSMC模拟的一个核心困难,本文拟采用增大电子质量三个数量级的方式对这一问题进行简化处理。电子的真实质量为9.11×10-31kg,增大三个数量级至9.11×10-28kg。以氧原子O为例,其质量为2.656×10-26kg,调整后的电子质量约为氧原子质量的3.4%。在温度相同的情况下,调整后电子的随机热运动速度均值比氧原子大不到一个数量级。同时,为保证化学反应过程质量守恒,增大电子质量须同步减小离子质量。以氧离子O+为例,真实质量为2.656×10-26kg,调整后的质量为2.5649×10-26kg,质量变化约为3.4%,亦不会对其热运动速度造成明显影响。调整后各离子的质量及其因调整而改变的比例见表 2.该表表明,离子质量改变率的最大值为N+的3.9%,对其热运动速度的改变亦在可以忽略的范围内。
| 离子 | 真实质量/kg | 调整后质量/kg | 变化率 |
| N2+ | 4.648×10-26 | 4.5569×10-26 | 2.0% |
| O2+ | 5.312×10-26 | 5.2209×10-26 | 1.7% |
| NO+ | 4.988×10-26 | 4.8969×10-26 | 1.8% |
| N+ | 2.324×10-26 | 2.2339×10-26 | 3.9% |
| O+ | 2.656×10-26 | 2.5649×10-26 | 3.4% |
经过上述处理之后,由于电子和离子的运动速度基本处于一个量级,整体上它们将一起作宏观运动,因此既无需将电子和离子进行强制关联,也无需担心电子因运动速度过快而疾速逃离计算区域,计算区域可维持近似电中性。
2 复杂外形航天器再入稀薄电离过程的DSMC程序设计 2.1 直角/非结构网格技术在DSMC方法中,网格的作用是选择可能的碰撞分子对以及对宏观参数取样。从计算的角度而言,流场采用大小均匀的直角坐标网格,追踪分子的效率非常高,计算区域内的模拟分子可以直接根据分子的位置坐标来确定分子所属网格,不必跟踪分子从一个网格到另一个网格的运动,但是其缺点是无法精确地描述物面边界条件。非结构网格在表征复杂外形方面具有高度适用性,并且容易实现正确的边界条件,但是追踪分子的算法比较繁琐和费时。本文结合直角坐标计算的高效率以及三角形非结构网格对航天器几何外形的精细描述,在描述物面几何形状的非结构网格建立以后,直接将其嵌入到直角网格的流场中,使DSMC计算对流场网格的依赖程度大大降低。
直角/非结构网格的详细陈述见文献[19]。
2.2 网格自适应方法DSMC方法的内在要求之一就是网格尺度须小于气体分子平均自由程。流场初始化时的网格设置是其尺度小于来流平均自由程,但是在超高速飞行的航天器头部,激波及波后密度显著增大,当地平均自由程变小,初始化的网格不能继续满足要求,需要对网格进行细化。本文采用两级直角坐标网格的策略,一级网格为初始化时形成的背景网格,二级网格为根据密度变化将背景网格加密之后形成的碰撞网格。
网格自适应参数通常有不同选取方式,较为普遍的是根据流场密度梯度变化确定,但是这种方式涉及流场密度的梯度计算。本文采用一种简化处理方式:初始时背景网格即为碰撞网格,设置碰撞网格分子数上限;随着流场演化,当碰撞网格中分子数大于上限时,将该网格在每个方向一分为二,即将该网格细分为八个网格;根据流场演化情况,不断重复上述过程,直到流场达到稳定状态。
2.3 DSMC并行算法考虑到极高速航天器再入稀薄和近连续过渡流电离过程的DSMC模拟计算量巨大,单一计算机计算速度慢且无法满足大量模拟分子导致的巨大内存需求,必须发展DSMC并行算法。本文采用区域分解的策略,根据计算的处理器数目将计算区域划分为等量的子区域,每个处理器在其分配的子区域内独立地计算模拟分子的碰撞和迁移,离开子区域的模拟分子把携带的信息传递给对应子区域的处理器。
如果模拟分子在运动一个时间步长之后,离开原先所在的网格迁移进入相邻的网格,并且改变后的网格隶属于其它的处理器,这样的分子及其携带的所有信息将被记录下来并放入缓冲数组。当所有的模拟分子被确定以后,放入缓冲数组的分子就在相应的处理器之间进行信息交换。
本文基于MPI并行程序设计函数,采用单一方向区域剖分,实现三维复杂外形航天器极高速再入稀薄气体电离过程的DSMC模拟。三维复杂外形航天器极高速再入稀薄气体电离过程的DSMC模拟,依据航天器尺寸和来流条件,通常需要数十至数百个计算核心。
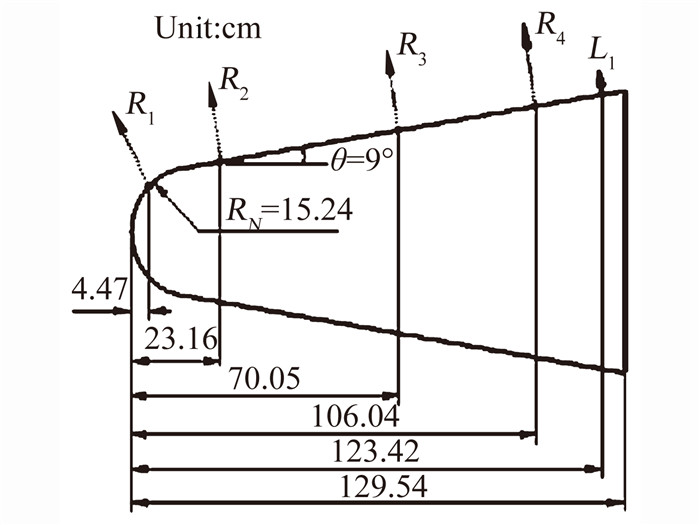
3 航天器再入稀薄电离过程的DSMC模拟 3.1 RAM-C Ⅱ飞行试验稀薄电离过程计算验证RAM-C Ⅱ飞行试验是目前可查到的仅有飞行试验电子密度测量公开案例,常作为检验电离计算模型和程序的经典算例。它于1960年代后期发射,以第一宇宙速度再入大气层,其外形如图 1所示。飞行试验中,沿着4个测点R1、R2、R3和R4测量这些方向上的最大电子密度值,沿着L1测量该方向上的电子密度分布情况。
|
| 图 1 RAM-C Ⅱ飞行试验测点分布 Fig. 1 Schematic of probe locations in RAM-C Ⅱ |
受网格尺度限制,本文计算状态采用81km高度,此处来流条件为:粒子数密度为3.275×1020/m3,其中21%为O2、79%为N2,压强为0.889Pa;来流温度为196.7K,对应声速为281.15m/s;来流速度为7800m/s,对应马赫数28.1;气体分子平均自由程为5.16×10-3m。壁面采用漫反射模型,温度取为1000K。取背景网格宽度5×10-3m,计算区域为[-0.25m, 1.55m]×[-0.5m, 0.5m]×[0, 0.5m],于是计算区域的网格数为360×200×100。采用60个CPU核进行并行计算,取时间步长为1×10-7s。
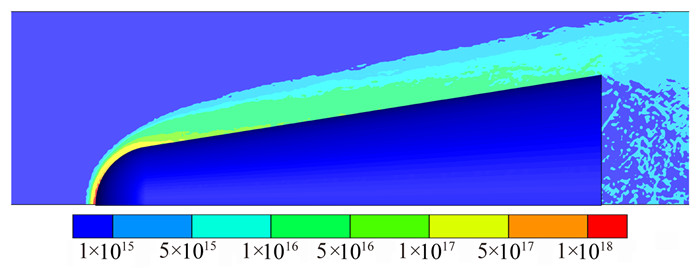
相对于RAM-C Ⅱ气动特性和流场特征,本文最为关注的是RAM-C Ⅱ周围的电子密度分布情况。RAM-C Ⅱ绕流流场的电子密度分布如图 2所示。该图表明,尽管经过较大样本的统计抽样,电子密度分布依然存在较大统计涨落,尤其是在尾流区域。造成这一现象主要有两个原因:一是DSMC方法不可回避的统计涨落,由于电子属于稀有组分,解决这一问题的根本方法是发展稀有组分粒子追踪方法[20-21];另一个原因是本算例的特殊性,81km高度属于稀薄过渡流区,粒子密度相对较小,同时RAM-C Ⅱ以第一宇宙速度再入,电离度很低,电子密度本身就很小。计算经验
|
| 图 2 RAM-C Ⅱ 81km处流场的电子密度分布 Fig. 2 Electron density distribution for RAM-C Ⅱ at 81km |
表明,随着再入速度的增大,统计波动将被明显抑制,这也是RAM-C Ⅱ算例经常被作为电离相关计算方法和程序考核标准的原因之一。
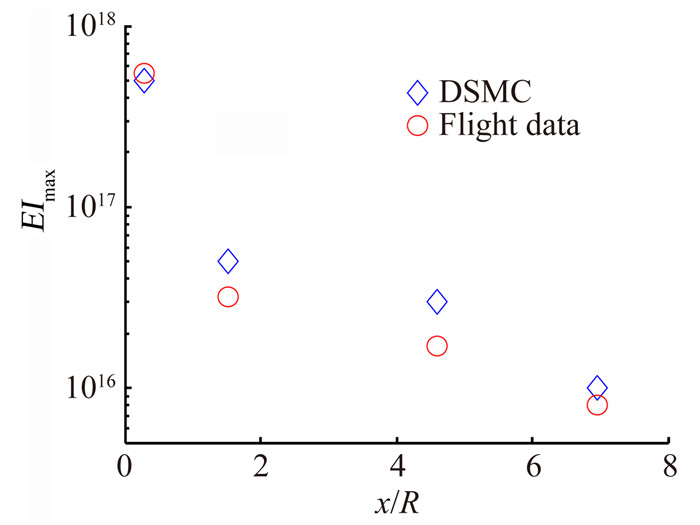
四个测点R1、R2、R3和R4方向的电子密度最大值如图 3所示。一般认为,电子密度计算值误差在3倍以内都是可以接受的。该图表明,尽管没有采用稀薄组分粒子追踪方法,本文发展的模型和计算方法得到的电子密度与飞行试验测量值仍能吻合较好。
|
| 图 3 测点方向的电子密度最大值与飞行试验比较 Fig. 3 Maximum electron densities along probe directions |
3.2 彗星探测器Stardust再入稀薄段电离特性计算分析
如前所述,彗星探测器Stardust实现了人造飞行器的最高飞行速度,它以12.8km/s的速度再入大气层,必将引起强烈的化学反应和电离过程。Stardust的外形如图 4所示,其球头半径为0.22m,头部半锥角为59.5°,肩部半径为0.02m,前后长度为0.5m,肩部半径为尾部半径为0.25m。为与参考文献对比,本文计算80km的高度,对应来流马赫数为45.5。同上例采用壁面漫反射模型,壁温取1000K。计算区域为[-0.3m, 0.6m]×[-0.6m, 0.6m]×[0, 0.6m]。采用36个核进行并行计算。

|
| 图 4 彗星探测器Stardust外形 Fig. 4 Configuration of Stardust |
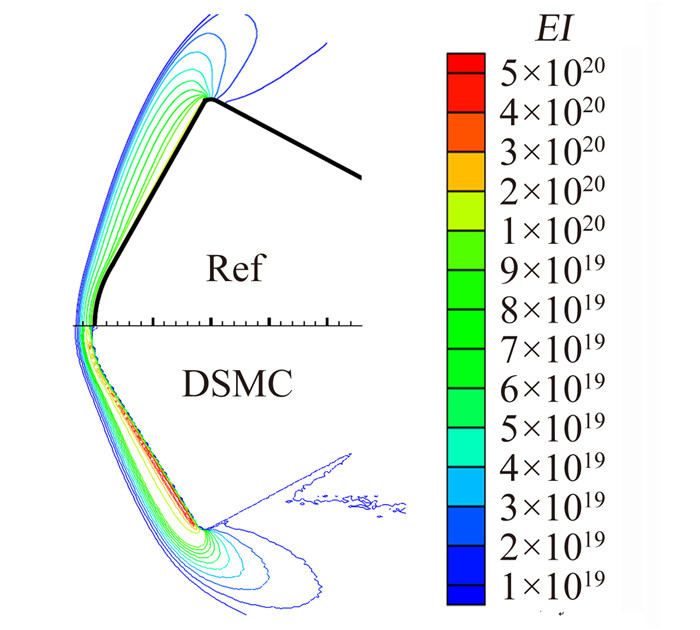
本算例关心的核心问题依然是绕流流场的电子密度分布,如图 5所示。该图表明,本文计算所得的电子密度分布与参考文献[1]吻合很好。尽管在等值线分布上存在一些细微差异,两者在电子密度分布的脱体距离、最大值上均完全吻合。该图还表明,对于Stardust这种以极高速度再入的航天器,其在80km高度处的电子密度高达5×1020/m3,较上例显著增大。这意味着此类飞行器的通信黑障区域将大幅向稀薄区域延伸,必须引起通信设计的高度关注。
|
| 图 5 80km处Stardust绕流电子密度分布 Fig. 5 Electron density distribution for Stardust at 80km |
4 结论
本文采用增大电子质量三个数量级并相应调整离子质量的方法,把电子当作一种普通分子对待,拓展DSMC模拟化学反应方法处理稀薄气体电离过程;采用单温度模型处理全部化学反应,对涉及电子的反应速率常数进行修正;以直角/非结构网格相结合,运用碰撞网格自适应方法,基于MPI并行环境,开发适于真实复杂外形的三维稀薄气体电离DSMC计算程序。通过计算RAM-C Ⅱ外形再入飞行高度81km绕流流场的电子密度,得到计算结果与飞行试验测量值吻合较好;计算Stardust外形以类第二宇宙速度再入飞行高度80km绕流流场的电子密度等值线云图,得到了与参考文献计算值一致的结果。相对于稀薄气体化学反应的DSMC方法,本文发展的模型和程序不会导致计算量的显著增大,可直接应用于三维复杂外形体极高速再入条件下的稀薄气体电离计算。
计算经验表明,RAM-C Ⅱ飞行试验是检验电离模型和算法的典型算例。彗星探测器Stardust在80km高度以12.8km/s速度再入时,流场电子密度高达5×1020/m3,这意味着此类飞行器的通信黑障区域将大幅向稀薄区域延伸,需要引起通信设计的高度关注,也为本文进一步深化研究指明了方向。
| [1] | Ozawa T, Zhong J, Levin D A, et al. Modeling of stardust reentry flows with ionization in DSMC[R]. AIAA 2007-611. |
| [2] | Anderson J D. Fundamentals of aerodynamics (5th edition)[M]. McGraw-Hill Education, 2010. |
| [3] | Chapman S, Cowling T G. The mathematiccal theory of no-uniform gases (3rd edition)[M]. Cambridge University Press, 1991. |
| [4] | Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2003, 193(2):708–738. |
| [5] | Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M]. Clarendon Press, Oxford, 1994. |
| [6] |
Wu Q F, Chen W F.
DSMC method for high temperature chemical nonequilibrium rarefied flows[M]. Beijing: National University of Defense Technology Press, 1999.
(in Chinese) 吴其芬, 陈伟芳. 高温稀薄气体热化学非平衡的DSMC方法[M]. 北京: 国防科技大学出版社, 1999. |
| [7] | Alexander F J, Garcia A L. The direct simulation Monte Carlo method[J]. Computers in Physics, 1997, 11(6):588–593. DOI:10.1063/1.168619 |
| [8] |
Fan J, Shen Q. The Monte Carlo direct simulation of the hypersonic nonequilibrium flow past a circular cylinder in transition flow regimes[J].
Acta Aerodynamica Sinica, 1995, 13(4):405–413.
(in Chinese) 樊菁, 沈青. 过渡领域高超声速圆柱绕流的直接模拟[J]. 空气动力学学报, 1995, 13(4) : 405–413. |
| [9] |
Li Z H, Wu Z Y. DSMC simulation on rarefied aerodynamics of Apollo-CM[J].
Acta Aerodynamica Sinica, 1996, 14(2):230–233.
(in Chinese) 李志辉, 吴振宇. 阿波罗指令舱稀薄气体动力学特征的蒙特卡罗数值模拟[J]. 空气动力学学报, 1996, 14(2) : 230–233. |
| [10] | Bird G A. Nonequilibrium radiation during re-entry at 10km/s[R]. AIAA 87-1543. |
| [11] | Carlson A B, Hassan H A. Direct simulation of re-entry flows with ionization[J]. Journal of Thermophysics & Heat Transfer, 2015, 6(3):400–404. |
| [12] | Boyd I D. Modeling of associative ionization reactions in hypersonic rarefied flows[R]. Center for Turbulence Research, Annual Research Briefs 2007. |
| [13] | Boyd I D. Modeling of plasma formulation in rarefied hypersonic entry flows[R]. AIAA 2007-206. |
| [14] | Fan J, Zhang Y H, Jiang J Z. Monte Carlo modeling of electron density in hypersonic rarefied gas flows[C]//29th International Symposium on Rarefied Gas Dynamics, 2014. |
| [15] | Shevyrin A A, Vashchenkov P V, Bonder Y A, et al. Validation of DSMC results for chemically nonequilibrium air flows against measurements of the electron number density in RAM-C Ⅱ flight experiment[C]//29th International Symposium on Rarefied Gas Dynamics, 2014. |
| [16] | Morsa L, Zuppardi G. Influence of ionization on the Gupta and on the Park chemical models[C]//29th International Symposium on Rarefied Gas Dynamics, 2014. |
| [17] | Gupta R N, Li K P, Thompson R A, et al. Calculations and curve fits of thermodynamic and transport properties for equilibrium air to 30000K[R]. NASA RP-1260, 1991. |
| [18] | Boyd I D. Modeling of associative ionization reactions in hypersonic rarefied flows[J]. Physics of Fluids, 2007, 19(9):1828–1837. |
| [19] |
Liang J. DSMC method on hybrid of cartesian and unstructured grid and its application[D]. Beihang University, 2014. (in Chinese). 梁杰.直角/非结构混合网格的DSMC方法及应用研究[D].北京航空航天大学博士毕业论文, 2014. |
| [20] | Boyd I D. Conservative species weight scheme for Direct Simulation Monte Carlo method[J]. Journal of Thermophysics & Heat Transfer, 2015, 10(4):579–587. |
| [21] | Fan J, Zhang Y H, Jiang J Z. An algorithm for trace species in hypersonic rarefied gas flows[C]//CSTAM 2012-B03-0417, 2012. |



