随着俄罗斯“暴风雪”超空泡鱼雷面世,发展以潜射导弹、高速鱼雷为代表的新型高速与超高速水中兵器,成为世界先进大国关注的重大课题。俄罗斯第二代速度达到200m/s的鱼雷正在研制过程中,美、德、英、法等国也都在进行超空泡减阻技术的基础与应用研究,我国也于近年开展了超空泡技术的基础研究[1-2]。
超空泡流动现象涉及到了多相流、湍流、相变、可压缩性和非定常等复杂流动机制,迄今对于这一复杂流动的了解还十分有限。早期研究主要以理论研究为主,辅助实验结果修正理论公式中的系数而得到一些经验公式。随着计算机硬件性能提升及现代CFD技术的飞速发展,超空化问题的研究已经发展出现代的基于Navier-Stokes方程的数值模拟技术。美国宾州大学学者Kunz、Lindau等,基于预处理技术,应用均质平衡流假设发展了空化流动模拟软件-UNCLE_M,可计算自然空化、通气空化。同时软件耦合了六自由度方程,可以计算航行体完整的弹道和姿态,在高速水下超空泡航行体流体动力的数值模拟方面发表了不少有影响的文章,代表了目前计算研究的方向[3-10]。国内上海交大陈鑫等基于SIMPLE算法,开发了可用于模拟自然、通气空化的软件[1, 11-13]。SIMPLE算法中组分输运方程与流场方程分离求解,对组分输运方程进行松弛即可保证稳定求解,但SIMPLE方法本身由不可压方法发展而来,在求解高速问题时需进行修正。
本文以可压缩预处理技术为基础,应用均质平衡流假设,发展了基于输运方程空泡模型的空化模拟代码。在基于输运方程空化模型中,液体的蒸发和水蒸气的凝结过程通过输运方程模拟实现,源项控制相间的相互转化。常温条件下,水蒸汽和液态水的密度相差1000倍,源项雅克比矩阵预处理后特征值与无黏通量雅克比矩阵特征值存在量级差异,常规对角化及简化谱半径方法在大的源项参数下难以获得收敛结果,出现“源项刚性”问题。在Kunz系列文章中,隐式化处理水的破坏项,水的生成项则采用显式松弛方式。本文采用点隐式方法处理整个源项,在近似因子
分裂基础上,分别应用了三种矩阵分裂技术,考察源项矩阵处理的影响,在LUSGS、AFADI方法上均实现了稳定计算。
1 数值模拟方法 1.1 控制方程在均匀一致、运动学、热力学平衡假设下,水、汽、不可凝结气体的两相流动可以描述为一种混合流体的单相流动。加入预处理的非定常无量纲控制方程如下[14]:
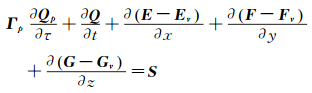
|
(1) |
上式中应用了“双时间”方法,τ为虚拟时间变量,t为物理时间变量。守恒变量定义为:
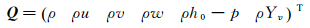
|
(2) |
原始变量选取:
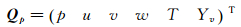
|
(3) |
应用原始变量有利于推导公式。E、F、G为无黏通量[14],Ev、Fv、Gv为黏性通量,源项S为:
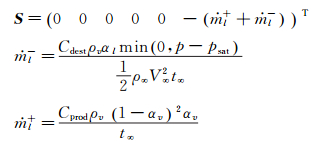
|
(4) |
式中psat为水的饱和蒸汽压。水的状态方程选用加入温度修正的Tait方程[15]:
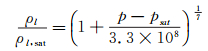
|
(5) |
气相采用完全气体状态方程:
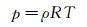
|
(6) |
对于含任意状态方程的流体混合物,应用Amagat相混合定律计算:
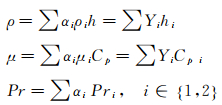
|
(7) |
其中Yi为组分质量分数,αi为组分体积分数。混合物密度及组分密度通过下式相联系:
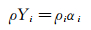
|
(8) |
由于空化计算涉及的水的流动速度一般在10m/s左右,流动马赫数为10-3量级,传统可压缩求解方法会遇到雅克比矩阵特征值相差量级导致的刚性问题,必须应用预处理技术[16]。通过在控制方程时间导数项前乘以预处理矩阵改变雅克比矩阵特征值,使所有特征值处在相同量级,达到消除方程刚性的目的。考虑多相的预处理矩阵Weiss-Smith[6]矩阵为:
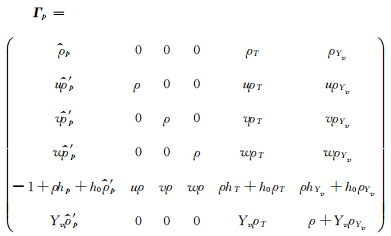
|
(9) |
变化到一般曲线坐标系推导可得基于原始变量的雅克比矩阵为:
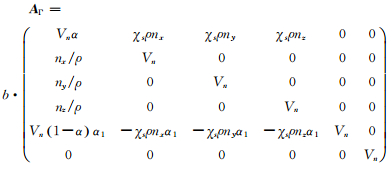
|
(10) |
雅克比矩阵其特征值及其它参数如下:
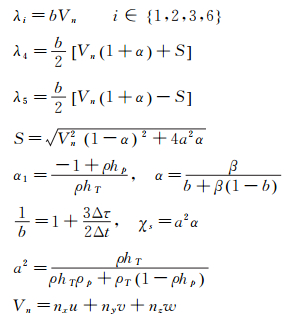
|
(11) |
上式中,b=1时,非定常预处理转化到定常预处理,而β=1时,方程回到无预处理情况。在求解非定常问题时,右端项需要定常雅克比矩阵及特征值[17],方程求解时左端项和右端项特征值不匹配问题通过限制局部时间步长来解决。本文应用Roe's FDS格式空间离散,在预处理情况下,Roe格式需根据预处理后的特征向量进行重构,标准的Roe格式如下:
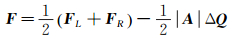
|
(12) |
第一项为通量项,不作修改,第二项为Roe格式的耗散项,以新的特征值作为耗散的尺度。
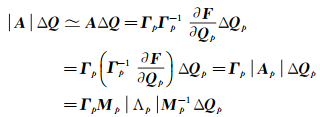
|
(13) |
修改后的Roe格式适用于全速域。当流场中出现局部超声速,应用HCL熵修正[18]技术保持计算稳定。
1.3 隐式时间离散首先,给出预处理方程在一般曲线坐标系下的表达式:
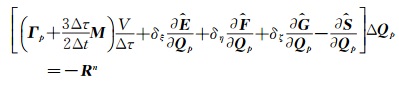
|
(14) |
令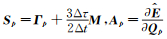
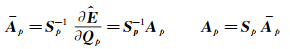
|
(15) |
式(14) 中A为方程基于原始变量的真实雅克比矩阵,且满足:
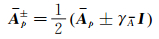
|
(16) |
因此,矩阵Ap的分裂可以写为:
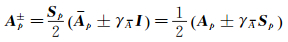
|
(17) |
为便于阐述,将式(14) 在一维情形下矩阵分裂得到:
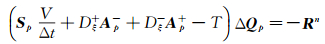
|
(18) |
空化计算中对源项矩阵T的处理至关重要,由于液态水的密度为水蒸气密度的1000倍以上,T的特征值往往比无黏项特征值大几个量级,采用类似黏性谱半径及矩阵对角化的方法会导致收敛极其缓慢,本文对其直接求逆。上式可以改写为:
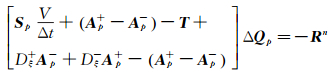
|
(19) |
对(19) 式可采用近似因子分裂。常规分裂方式是将源项雅克比矩阵放入对角线上,即:
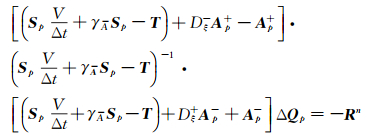
|
(20) |
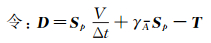
|
(21) |
注意到:
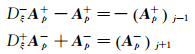
|
(22) |
将式(20) 写成LUSGS分裂格式:

|
(23) |
式(20) 的求解每一步迭代需要对D矩阵求逆2次。将式(19) 中的源项矩阵T写到L扫描中,可以得到如下近似因式:
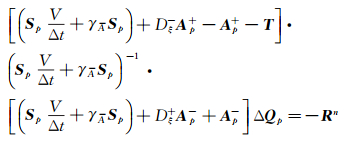
|
(24) |
式(24) 与式(20) 相比,L扫描完全一致,U扫描中无源项矩阵T。这样做的好处是减少了矩阵求逆次数,可以大大节省计算时间。同时,也可将T矩阵移到U扫描,过程与移到L扫描类似。
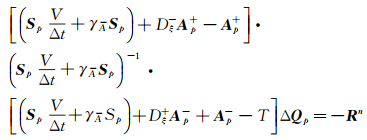
|
(25) |
对式(14) 的离散还可采用DDADI方法,令:S=SpV/Δt,近似因子分裂得到:
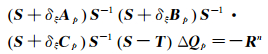
|
(26) |
这样分裂后,三个方向的矩阵算子均可以对角化,将无法对角化的源项矩阵移到最后,与单相流动求解相比,仅需在三个方向扫描后增加一次矩阵求逆。
在含相变问题求解中,限制相变剧烈区时间步长可以获得收敛过程平缓的结果。与文献[19]不同,本文采用下式限制空化区时间步长:

|
(27) |
式中下标“inv”、“vis”、“sor”分别代表无黏、黏性、源项贡献。
1.4 湍流模型及初边值界条件湍流模型应用k-ω SST两方程模型,在空化流动中,标准湍流模型过高预测空泡尾部湍流黏性,抑制空泡脱落,在流动非定常效应较强,湍流黏性系数还需要加入Coutier-Delgosha空化修正:
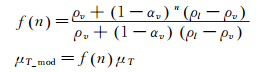
|
(28) |
在不涉及底部分离算例中,初场可以选择为来流值;在计算大分离算例时,以全湿流的计算结果为初场可以稳定计算。
边界条件主要有远场边界、固壁边界、对称边界、奇性轴边界等,与单相流类似处理。
2 计算结果 2.1 NACA0015水翼空化计算NACA0015水翼算例为国外发布的考核空化计算软件的标准算例,计算参数:p∞=0.12×105(空化),V∞=3.41m/s,T∞=300K,psat=3752Pa,迎角已经预偏4°。
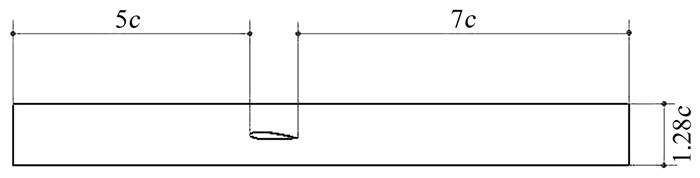
|
| 图 1 NACA0015水翼计算外形简图 Fig. 1 NACA0015 hydrofoil configuration |
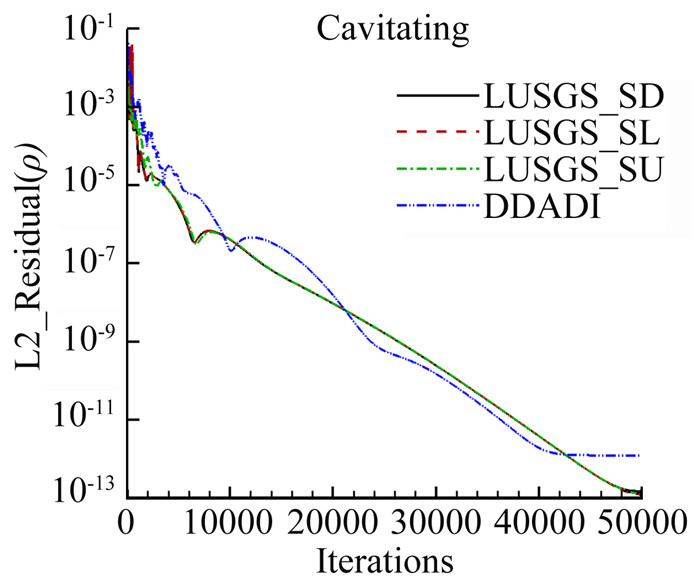
计算中Cdest=104,Cprod=100,隐式格式分别采用1.4节中的四种方法,记式(19) 为LUSGS_SD,式(23) 为LUSGS_SL,式(24) 为LUSGS_SU,式(25) 为DDADI。计算的残差和收敛曲线及升力系数收敛曲线见图 2、图 3。水翼壁面为黏性固壁,水洞壁为无黏固壁,入口和出口指定为远场,以来流初始化流场。
|
| 图 2 残差收敛曲线比较 Fig. 2 Comparison of convergence history curve |
|
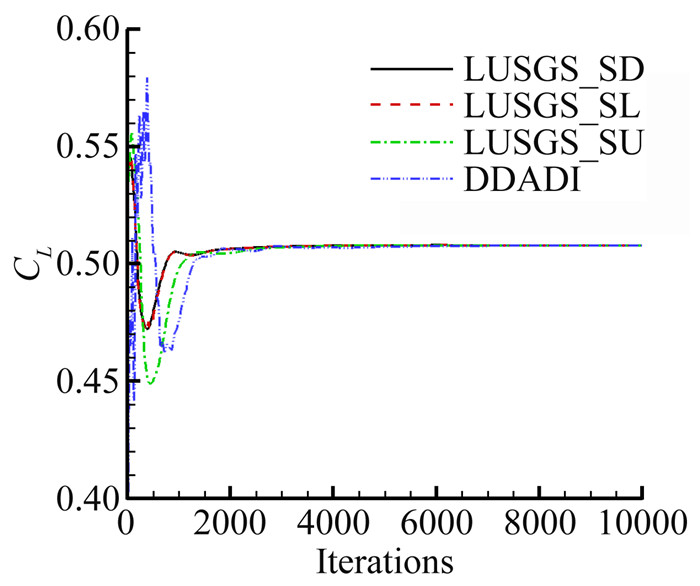
| 图 3 升力系数收敛曲线对比 Fig. 3 Comparison of lift curve |
图 2的残差收敛曲线表明,采用的四种隐式算法计算在空化情况下连续方程残差L2模可以收敛至10-10以下。LUSGS的三种分裂方式收敛曲线在迭代4000步以后的形态完全一致;LUSGS_SD对D矩阵求逆2次,耗时最多,但在流场“暂态”期稳定性最好;LUSGS_SU、LUSGS_SL分别仅在LUSGS的U、L扫描中考虑源项作用,如果局部时间步长不采用源项限制,在计算初期残差振荡,甚至导致计算发散。
图 3为升力系数曲线对比,可以看到,LUSGS_SD和LUSGS_SL几乎完全一致,而LUSGS_SU和前二者差别较大是由于局部时间步长加了限制。DDADI则由于稳定性较差,计算中加入了更多其他稳定性措施,导致收敛较慢,还有改进空间。四条曲线在迭代步数八千步后完全重合,与隐式方法不影响收敛结果的论断相符。
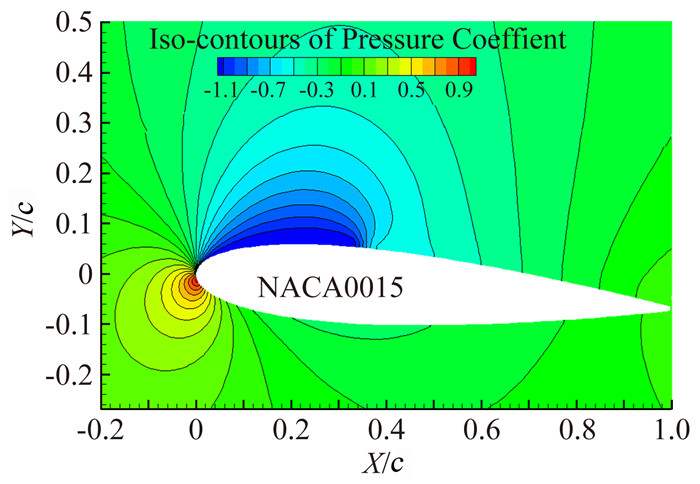
从图 4的压力系数等值线流场可以看到,随着流动从前缘向后发展,压力逐渐降低,当压力低于饱和蒸汽压时,发生自然空化;空泡随着流动向后逐渐扩大,泡内压力保持为常数;空泡在翼型中部闭合,闭合区引起回射流,导致出现较大的压力梯度,与超临界翼型翼面发生激波的图像类似。
|
| 图 4 压力系数等值线 Fig. 4 Contour of pressure coefficient |
2.2 锥柱体算例
Rouse和McNown研究了一系列典型回转体的空化现象,并发布了实验结果。本文选择了外形简单的22.5°锥柱体算例对本文发展的方法进行进一步验证。算例参数:V∞=4.3m/s,T∞=300K,psat=3589Pa,空化数σ=0.3、0.4、0.5,全湿流状态。
计算采用三维计算,网格取C型网格,网格维数113×65×17(流向×法向×周向),壁面最小距离Δn=4×10-4,壁面第一层网格y+≈1-3。Cdest=104,Cprod=100。
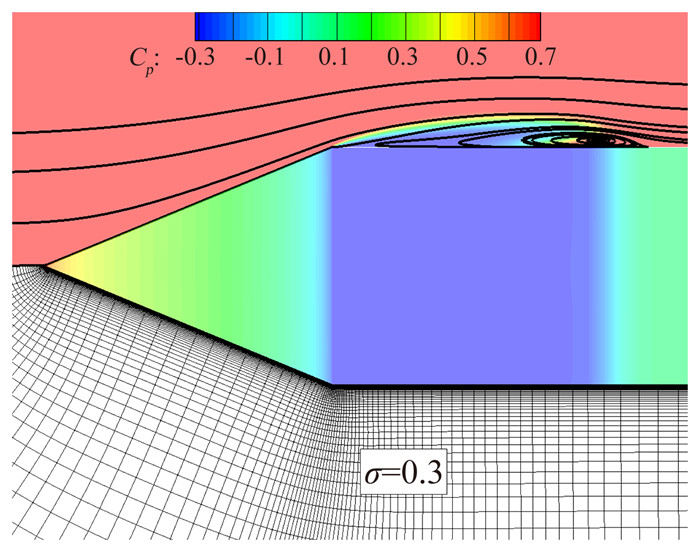
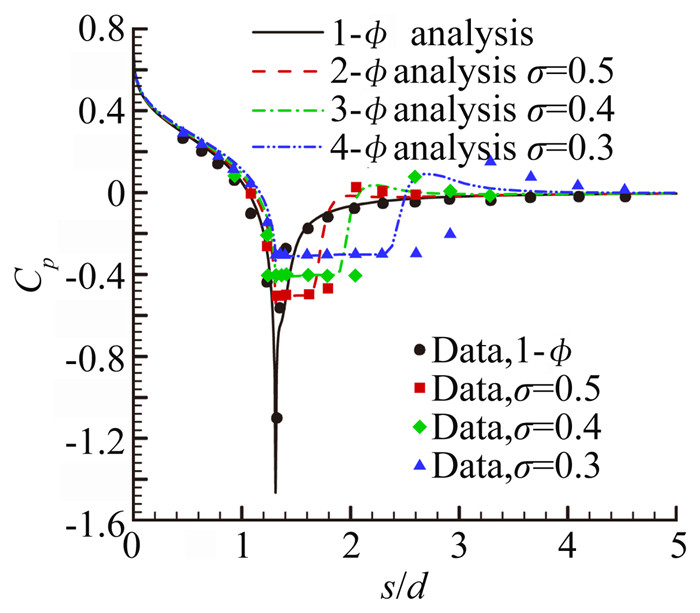
图 5为σ=0.3计算结果,流动在过尖锥后流动发生空化,空化区压力系数近似为常数,空化区形成大的分离区。从图 6压力系数比较曲线看到,随着空化数降低,空泡长度增大,回射流现象更剧烈。本文计算结果与试验数据基本一致, 较为准确地捕捉了空泡的起始以及闭合区域位置。
|
| 图 5 锥柱体流场图 Fig. 5 Flow field of cone cylinder |
|
| 图 6 壁面压力系数比较曲线 Fig. 6 Comparison of wall pressure coefficient |
3 结论
本文在可压缩方法框架下,通过应用低速预处理技术发展了基于混合模型的多相、多组分的数值计算方法,对NACA0015水翼与锥柱体标模的验证计算表明:
1) 源项处理方式合理,LUSGS的三种隐式分裂及DDADI方法均能获得稳定收敛解,残差可以降到机器零;
2) 计算结果与试验值基本一致,所采用的算法能准确地捕捉到空泡的起始及溃灭。
下一阶段将对通气空化进行验证计算研究,同时考虑加入六自由度计算模块模拟出水现象。
| [1] |
Chen Xin. An investigation of the ventilated cavitating flow[D]. Shanghai:Shanghai Jiaotong University, 2006.(in Chinese). 陈鑫.通气空泡流研究[D].上海:上海交通大学, 2006. |
| [2] |
Liu Hua, Li Jiachun, He Yousheng, et al. Suggestion on the research frame programme on hydrodynamics for the eleventh five year plan[J].
Advances in Mechanics, 2007, 37(1):142–147.
(in Chinese) 刘桦, 李家春, 何友声, 等. 十一五水动力学发展规划的建议[J]. 力学进展, 2007, 37(1) : 142–147. |
| [3] | Kunz R F, Boger D A. A preconditioned navier-stokes method for two-phase flows with application to cavitation prediction[R]. AIAA, 1999-3329, 1999. |
| [4] | Venkateswaran S, Lindau J W, Kunz R F, et al. Computation of multiphase mixture flows with compressibility effects[J]. Journal of Computational Physics, 2002, 180:54–77. DOI:10.1006/jcph.2002.7062 |
| [5] | Lindau J W, Sankaran V, Kunz R F, et al. Development of a fully-compressible multiphase Reynolds-averged Naviar-Stokes model[R]. AIAA CFD Conference, AIAA 2001-2648, Anaheim, CA, 2001. |
| [6] | Kunz R F, Boger D A, Stinebring D R, et al. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation predication[J]. Computers and Fluids, 2000, 29:849–875. DOI:10.1016/S0045-7930(99)00039-0 |
| [7] | Li D, Venkateswaran S, Lindau J, et al. A unified computation formulation for multi-component and multi-phase flows[R]. AIAA-2005-1391, Reno, NV, January 10-13, 2005. |
| [8] | Kinzel M P. Computational techniques and analyse of cavitating fluid flows[D]. The Pennsylvania State:University the Graduate School Department of Aerospace Engineering, 2008. |
| [9] | Kinzel M P, Willits S M, Lindau J W, et al. CFDSimulations of oscillating hydrofoils with cavitation[C]//The 44th Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2006. |
| [10] | Kunz R F. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies[R]. FEDSM99-7364, 1999. |
| [11] |
Chen Ying. Study of the numerical method for natural cavitating flow[D]. Shanghai:Shanghai Jiaotong University, 2009.(in Chinese). 陈瑛.自然空泡流数值模拟方法研究[D].上海:上海交通大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10248-2010033176.htm |
| [12] |
Guo Jianhong. Study of the numerical simulation method for complex multiphase cavitating flow[D]. Shanghai:Shanghai Jiaotong University, 2013.(in Chinese). 郭建红.复杂多相空泡流的数值模拟方法研究[D].上海:上海交通大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10248-1014008326.htm |
| [13] |
Zhou Jingjun. Numerical simulation study on the ventilated supercavitating flow and hydrodynamics of vehicle[D]. Harbin:Harbin Institute of Technology, 2011.(in Chinese). 周景军.通气超空泡流动及航行体流体动力数值模拟研究[D].哈尔滨:哈尔滨工业大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10213-1012000458.htm |
| [14] | Tian Ming. Numerical simulation of the internal two-phase flow within an aerated-liquid injector and its injection into the corresponding high-speed cross flow[D]. North Carolina State University, 2005. |
| [15] | Koop Arjen, Hoeijmakers Harry. Numerical simulation of unsteady three-dimensional sheet cavitation[C]//The 7th International Symposium on Cavitation. Ann Arbor, Michigan, USA, 2009. |
| [16] |
Mou B, Xiao Z Y, Liu G, et al. Low speed preconditioning for Roe scheme[J].
Acta Aerodynamica Sinica, 2010, 28(2):125–131.
(in Chinese) 牟斌, 肖中云, 刘刚, 等. 基于Roe格式的低速预处理方法研究[J]. 空气动力学学报, 2010, 28(2) : 125–131. |
| [17] | Buelow P E O, Schwer D A, Feng Jinzhang, et al. A preconditioned dual-time, diagonalized ADI scheme for unsteady computations[R]. AIAA-97-2101, 1997. |
| [18] | Lin Hong-Chia. Dissipation additions to flux-difference Splitting[J]. Journal of Computational Physics, 1995, 117:20–27. DOI:10.1006/jcph.1995.1040 |
| [19] | Gerlinger P. An implicit multigrid method for the simulationof chemically reacting flows[J]. Journal of Computational Physics, 1998, 146:322–345. DOI:10.1006/jcph.1998.6061 |



