减少航空飞行器的阻力一直是飞机设计师和空气动力学工作者的追求目标,而飞行器的气动阻力主要由压差阻力和摩擦阻力组成,压差阻力可以由壁面压力积分得到,但是摩擦阻力的测量则相对困难得多。典型运输机的摩擦阻力甚至占总阻力的35%[1],因此在飞行器的减阻研究中,减少摩擦阻力是重要途径之一,而摩擦阻力的精确测量又是减阻研究中的重要研究手段。
摩擦阻力测量技术经过多年的发展,现有的手段主要分为直接和间接测量方法[2],直接测量方法有摩阻天平、MEMS摩阻传感器等、位移差动传感器,间接测量方法则一般基于介质流体的运动传递性模拟当地的摩擦力信息,例如液晶摩阻测量技术、油膜法、薄膜S3F (surface stress sensitive film,表面载荷应变膜) 技术。其中,摩阻天平方法需要考虑到天平安装对于模型结构的特殊加工要求,且天平与模型之间的安装间隙对于流场存在较大干扰;MEMS摩阻传感器除需考虑传感器与模型之间的形位公差和安装缝隙之外,还需要考虑风洞环境对于传感器的影响,例如温将、电磁干扰引起的传感器测量结果误差;而液晶摩阻测量技术在光路布置、标定上有着较大的难度,且所得结果的精度也存在很大误差,这些因素一直限制着液晶摩阻测量技术的发展。
薄膜S3F技术是一种压力/剪切力应变薄膜,弹性薄膜在受到压力/剪切力的作用下产生一定的形变,通过光学测量手段得到当地的形变量即可根据弹性薄膜的扬氏模量计算当地的法向力(压力) 和切向力(剪切力)。澳大利亚的Monash大学的Omid Amili等人以此对一维全湍管流的壁面摩擦力进行了测量[3];美国俄亥俄州的ISSI公司Sergey D.Fonov等人在2004年对其设计的S3F薄膜进行了实验室标定并对75°三角翼的表面摩擦力进行了测量[4],在2010年对后缘台阶流动(backward facing step flow)、圆柱绕流的表面分离及附着流动信息进行了测量[5]。
油膜法包括油膜干涉技术和近年来发展的光学流动方法。国外对油膜法的研究较多,墨尔本大学的Madad等人运用油膜法对零压和逆压梯度附面层的摩擦力进行了测量[6],俄罗斯的R. V. Nestulya等人用漫射照明获取薄油膜等厚度干涉条纹谱[6],美国S. A. Woodiga和Tianshu Liu运用光学流动技术对三角翼的摩擦力场进行了测量[7]。
荧光油流摩擦力场测量技术是在荧光油流技术(Illuminated Oil) 基础上结合光学流动技术(Optical Flow) 发展而来[8],是定性测量向定量测量的转变,具有很好的应用前景。荧光油流技术提供表征模型当地油膜在剪切力作用下的运动信息,然后采用光学流动技术进行数据处理,得到模型表面当地的摩擦力分布情况。其中,光学流动技术[9]即通过检测一组连续拍摄的图像的灰度变化以确定图像中目标油膜的运动情况,在20世纪80年代由计算机视觉专家提出,在90年末光学流动技术作为互相关技术的备选技术用于PIV技术试验,其后,光学流动技术开始应用于流场测量领域。
荧光油流摩擦力场测量技术可以得到全局摩擦力场,与油膜干涉方法相比,测量范围更大且对试验操作要求更低。该项技术运用荧光油流技术作为原始数据获取手段,对表面流场进行可视化测量,通过光流数据处理方法[10-11]得到表面流场的拓扑结构,然后根据DLT投影算法,并给定模型表面当地剪切力和当地网格法向的向量关系,进行三维摩擦力场的投影计算,得到三维曲面模型的表面摩擦力分布信息。
本文运用荧光油流摩擦力场测量技术,在低速风洞进行了平板模型、75°三角翼模型、角区模型的表面摩擦力分布测量。其中,平板模型试验是在我院的FL-5风洞[12],角区模型和75°三角翼模型试验在沈阳航空航天大学的SHDF风洞进行[13-14]。
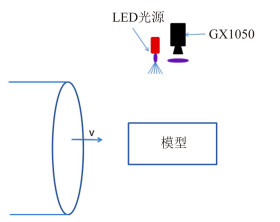
1 实验设计 1.1 FL-5风洞的平板试验实验在中航工业空气动力研究院哈尔滨院区的FL-5风洞进行[8]。该风洞是单回流式开口低速风洞,试验段为圆形截面,直径1.5m,长1.95m,风洞最大最大风速50m/s,在进行试验时,一般流场稳定时间在7s~10s。该次实验所用模型为前缘无下劈的有机玻璃制平板,平板模型长0.99m、宽0.4m,在下表面在30%、60%弦长处以两根细横梁支撑数据采集设备和光源安装于模型上方支架上,安装位置如图 1所示,激发出紫外光LED光源安装于正上方使其能够对三角翼进行完整照射;高速相机紧挨LED光源同样处于试验段中心线上,在相机镜头前加装滤镜,过滤模型表面反射的紫外光,相机帧速25fps,记录吹风全过程[8]。
|
| 图 1 FL-5风洞试验布置图 Fig. 1 Sketch map of wind tunnel test |
试验所用荧光涂料采用指定黏度的甲基硅油和汽车荧光检漏剂按照一定的配比调配而成,使用优质羊毛刷轴向涂刷,涂刷后静置片刻待涂料在表面扩散形成均匀厚度油膜;清洁时,采用蘸有丙酮的脱脂棉对模型表面残留涂料进行清理,完毕后静置几分钟至丙酮挥发后再次进行涂料涂刷工作。
设计试验状态为:迎角0°,平板模型风速为40m/s、雷诺数为2.495×105。
1.2 SHDF风洞的三角翼模型和角区模型试验该风洞实验段长3m、宽1.2m、高1m;空风洞实验段风速:0.2m/s~55m/s,湍流度小于0.14%。该风洞支撑系统为尾支,迎角范围:-6.3~20°,侧滑角范围:-40°~40°。试验模型为75°平板三角翼、角区模型。
其中,75°平板三角翼,弦长250mm,展长134mm,前缘有30°向下尖劈角,采用尾部支撑方式与风洞迎角控制弯刀连接。角区模型为Rood翼型--平板组合体,Rood翼型弦长383.3mm,展长235.1mm,底座平板长度为125cm,宽度为40cm,模型表面喷涂白漆增加底部反光。
试验中采用GX1050高速相机采集连续时间轴图像,最高帧速112fps,分辨率1024×1024,每秒最大传输数据量为240MB/s,试验结果存为8bits无压缩TIFF图片。相机安装于三脚架上,试验时安装在风洞上壁观察窗外或者右侧观察窗外,如图 2所示。

|
| 图 2 试验风洞及相机安装 Fig. 2 Wind tunnel and mounted camera |
试验中采用甲基硅油作为荧光指示剂的载体,选用汽车检漏剂作为荧光指示剂,激发光源为紫外光LED;为消除环境光和模型表面反射的影响,在相机镜头前加装带通滤镜,且将试验段的观察窗除相机和光源位置外全部用黑色胶纸粘贴。试验时整个试验段用挡光布进行遮挡,以此降低环境光的影响,提高信噪比。涂料用高压氮气通过空气喷枪进行模型表面的油料喷涂。
2 数据处理和分析 2.1 数据处理简介根据动量方程,并运用变量代换得到摩擦力计算方程:
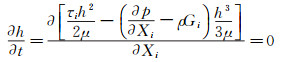
|
(1) |
式中,Xi为模型表面参考系坐标Xi=(X1, X2),h为油膜厚度(h1,h2),τ=τi(i=1, 2) 为摩擦向量,p为压力,G=Gi(i=1, 2) 为重力向量,μ为黏度系数。
令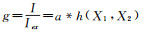
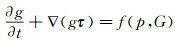
|
(2) |
当摩擦力的空间变化很小(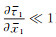
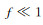
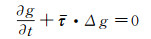
|
(3) |
该式即为摩擦力计算判据式。
如果可以得到油膜厚度分布情况,根据式(3) 可以解得摩擦力信息,但是因为油膜厚度与光强的关系无法通过简单标定或者算式推导得到,故在缺少约束前提下无法解得τ, 为保证τ的各项连续性应用经典的Horn-Schunck方法进行正交化。经过归一化计算得到摩擦力相对当地油膜厚度(荧光光强) 的相对摩擦力信息。
2.2 平板模型数据处理结果试验状态:迎角0°,风速40m/s,试验雷诺数Re=2.495×105,试验结果如图 3、图 4所示。

|
| 图 3 试验原始图像 Fig. 3 Original experiment image |

|
| 图 4 平板模型的摩擦力分布 Fig. 4 Skin friction distribution of flat model |
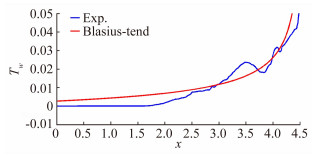
为验证该计算结果的准确性,根据平板层流的Blasius理论解与模型中心弦线处的摩擦力随弦长的变化关系做出图 5。
|
| 图 5 Blasius层流理论解和试验结果的趋势对比 Fig. 5 Comparing of Blasius-lamiar solution and experiment result |
其中,图 3为试验中油膜稳定运动的某一时刻试验图像,表征的是该瞬时该模型表面的油膜发展状态;图 4为处理结果的相对摩擦力分布云图;图 5中红线为Blasius层流理论解的趋势,纵坐标Tw为相对摩擦力值,蓝线为实际试验结果随弦长的变化趋势,蓝线部分截取的部分是平板前缘再附后的部分,即图 4中红色分水岭式摩擦力分布之后的部分,在趋势上试验结果与理论解基本一致。
荧光油流计算结果与平板层流理论解在数值上有所差距,其主要原因是模型前缘分离导致部分区域流场结构不同,层流解不完全类同于试验状态;荧光油流计算结果未精准标定。可以提供精准单点摩擦力测量的方法较多,.在后期的研究中可以尝试对荧光油流的相对摩擦力信息进行必要的标定,从而得到整个测量面的摩擦力分布情况。
此外,该平板模型前缘未进行劈角,而是普通直角边,有别于经典的下劈角式尖前缘平板模型,因此气流在前缘处因直角边绕流和前缘分离,故出现图 4中的分水岭式摩擦力分布。
2.3 三角翼模型数据处理结果试验状态为迎角10°和20°,风速30m/s,试验雷诺数Re=4.725×104,试验结果如图 6和图 7所示。

|
| 图 6 三角翼模型试验图像 Fig. 6 Experiment image of delta wing model |
|
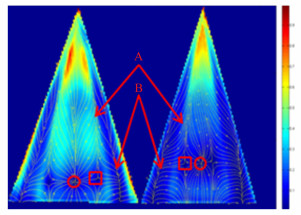
| 图 7 75°三角翼表面摩擦力分布和摩擦力线 Fig. 7 Skin friction distribution and friction line of 75° delta wing |
在图 6和图 7中,左侧为10°迎角,右侧为20°迎角,其中,图 7中,A为再附线,B为二次分离线,方框为鞍点,圆圈为结点。对比两种迎角下的流场结果可以看到,随着迎角增大,附着线的位置向边缘靠近,前缘分离极其靠近前缘,模型尾部两个鞍点和一个结点的的位置向模型前端移动,模型上表面摩擦力减小,且摩擦力集中区域向翼尖位置移动,模型后部的分离区域进一步扩大。
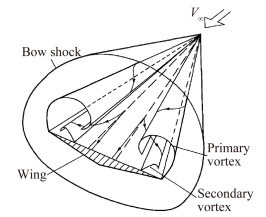
对比图 8中的典型三角翼流场结构[15],本期试验的计算结果在流场结构上与典型三角翼流场结构一致。
|
| 图 8 典型三角翼流场结构 Fig. 8 Classical flow field of delta wing |
2.4 角区模型数据处理结果
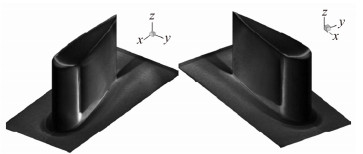
根据立体视觉技术对试验图像进行处理,得到如图 9所示的模型表面荧光油流分布情况。
|
| 图 9 角区模型的表面荧光油流分布情况 Fig. 9 Luminescent oil distribution of juntion model |
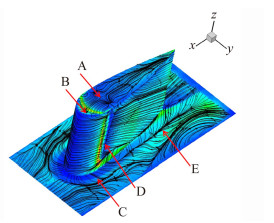
进行三维摩擦力信息计算时,先分块对各测量区域的油膜流动进行图像平面内的摩擦力计算,然后根据DLT投影和曲面模型当地法向与剪切力的关系计算得到当地的摩擦力信息,包括大小和方向。0°迎角和6°迎角下的计算结果如图 10和图 11所示,图中模型表面红色至蓝色摩擦力由大至小。
|
| 图 10 迎角0°时摩擦力分布和摩擦力线 Fig. 10 Skin friction distribution and friction line, AOA=0° |
|
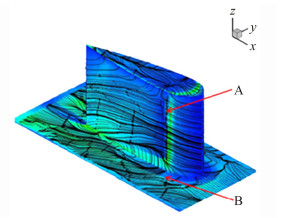
| 图 11 迎角6°时摩擦力分布和摩擦力线 Fig. 11 Skin friction distribution and friction line, AOA=6° |
图 10中,A为鞍点,B为二次分离线,C为绕翼型马蹄涡分离线,D为翼面分离线,E为马蹄涡二次分离线。
图 11中,相较0°迎角的情况,A处是因为出现迎角下翼面分离减小;下侧底面马蹄涡尺度减小,上侧底面马蹄涡尺度增大。
3 结论(1) 平板流动中,在层流状态下计算结果与Blasius层流解趋势一致;
(2) 由75°三角翼的计算结果可以看出,对于流场结构的计算与典型三角翼流场结构吻合,此外通过计算还可以得到整个模型上表面的摩擦力分布趋势并推断其流场发展规律;
(3) 文章得到了角区流动三维模型的表面摩擦力分布,其旋涡结构和分离位置与流动规律相吻合。
从各模型的计算结果可以看到,即使是0°偏航角下,摩擦力也会出现一定程度的非对称性,这可能是由流场湍流度、模型安装偏航角甚至模型加工精度等因素引起。
| [1] | John Green. Laminar flow control-back to the future[R]. AIAA 2008-3738. |
| [2] | Jonathan W Naughton. Modern developments in shear stress measurement[J]. Preprint submitted to Progress in Aerospace Sciences, 2002, 38(6-7):515–570. DOI:10.1016/S0376-0421(02)00031-3 |
| [3] | Omid Amili, Julio Soria. Wall shear stress distribution in a turbulent channel flow[C]//15th Int Symp on Application of Laser Techniques to Fluid Mechanics, 2010. |
| [4] | Sergey D Fonov, et al. Surface pressure and shear force fields measurements using elastic polymeric film[C]//11th International Symposium on Flow Visualization. August 9-12, 2004. |
| [5] | Sergey D Fonov, et al. Demonstration of a surface stress sensitive film for skin friction measurements in a variety of flows[C]//27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 28 June-1 July 2010. |
| [6] | Madad R, Harun Z, Chauhan K, et al. Skin friction measurement in zero and adverse pressure gradient boundary layers using oil film interferometry[C]//17th Australasian Fluid Mechanics Conference. 5-9 December 2010. |
| [7] | Nestulya R V, Nikiforov S B, Pavlov A A. Developement of the oil film method of skin friction measurement for curved and free oriented surfaces[J]. Experiments and Measurements In Fluid Mechanics, 1999, 13(2):1–9. |
| [8] | Woodiga S A, Liu T S. Skin friction fields on delta wings[J]. Exp. Fluids, 2009, 47:897–911. DOI:10.1007/s00348-009-0686-6 |
| [9] | Liu T S, Wang B, Woodiga S. Physics-based optical flow method in global flow diagnostics[C]//27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 2010. |
| [10] | Liu T S, Montefort J, Woodiga S, et al. Global luminescent oil-film skin-friction meter[J]. AIAA Journal, 2008, 46(2):476–485. DOI:10.2514/1.32219 |
| [11] | Shen L X, Liu T S. Global skin friction diagnostics in separated flows using luminescent oil[J]. Journal of Flow Visualization & Image Processing, 2009, 16:19–39. |
| [12] |
Wang Peng. Skin friction measurement of XX model in FL-5wind tunnel[R]. AVIC ARI, 2014-09-30. 王鹏. FL-5风洞XX模型表面摩擦力场测量试验[R].中国航空工业空气动力研究院, 2014-09-30. |
| [13] |
Wang Peng. Luminescent oil flow skin friction measurement in SHDF[R]. AVIC ARI, 2012-09-15. 王鹏. SHDF荧光油流摩擦力测量试验[R].中国航空工业空气动力研究院, 2012-09-15. |
| [14] | Zhong H J, Sudesh Woodiga, et al. Skin-friction topology of wing-body junction flows[J]. European Journal of Mechanics B/Fluids, 2015, 53:55–67. DOI:10.1016/j.euromechflu.2015.04.002 |
| [15] | Monson D J. A nonintrusive laser interferometer method for measurement of skin friction[J]. Experiments in Fluids, 1983, 1:15–22. DOI:10.1007/BF00282262 |



