高超声速飞行器在做高速飞行时,飞行器的壁面边界层流动是一个非定常的复杂的演化过程,其中的速度、密度、压力、温度等参数的时空分布十分复杂。从光学的观点看,当流场的密度发生变化时,其对应的折射率也将发生变化,如果此时一束光穿过该流场,那么因折射率的变化,光束所成的像将发生畸变,包括偏折、模糊和抖动,这种现象物理上称为气动光学效应[1]。
对于边界层气动光学的理论研究开始于Liepmann的分析[2],从几何光学线性理论的角度出发研究了小孔径光束(或称细光束),传播的偏折角均方根,同时引入湍流尺度和相关函数概念,建立了它们与密度、折射率以及时均光学偏差的统计结果的函数关系。1969年,Sutton从理论上研究了光敏流体中光线衰减问题[3],推导出衰减系数与湍流积分尺度的关系,再引入光学中的Lambert定律,得出反映光学畸变的均方相位误差的链接方程。Jumper et al.研究了Liepmann和Sutton的结果,论证了两者的结论是等价的[4]。此外,为了更好地应用链接方程,Jumper et al. [5], Gordeyev et al. [6-7], Wyckham et al. [8-10]等通过一系列的研究给出了在亚声速、跨声速、超声速以及高超声速的情况下链接方程中的比例系数。
这些研究主要包含两方面的特点,一是探讨的重点主要是光学和力学中的统计量(即偏折角均方根和平均意义上的来流参数及边界层厚度) 之间的关联,即建立和应用链接方程,二是关注点主要集中在所谓的湍流边界层。前者意味着研究的深度还没有拓展到对于脉动量的分析,比如光束偏折角时间序列的特性,后者意味着边界层的研究进展,尤其是边界层转捩研究的成果,还没有被引入到气动光学效应的分析中来。
针对上述研究的这些特点,本文视角集中于高超声速边界层转捩过程的气动光学效应问题,以细光束穿过边界层为具体实例,对其中的流场和光传播情况进行分析,得到在边界层转捩过程中光束抖动与壁面热流之间的某种关联。同时,开展了高超声速边界层转捩对细光束抖动特性影响的实验,结果验证了上述分析的关联性结果。这种理论和实验结果上的一致性,为我们提供了一种诊断高超边界层转捩问题的新思路和新技术。
1 转捩边界层的光传输效应从光学的观点出发,考虑一束小口径光束(或称细光束) 穿过平板边界层的情况。边界层流场中的密度分布与折射率分布存在如下关系:
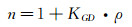
|
(1) |
其中,n表示折射率,ρ为密度,KGD是气体的一个常数,即Gladstone-Dale常数。公式(1) 即(Gladstone-Dale公式) 表明,在以折射率为代表的光学量和以密度为代表的流场量之间,存在一座桥梁。
以下对边界层流场具体分析,对于气体边界层流场,可将理想气体状态方程p=ρRT带入Gladstone-Dale公式,将得到:

|
(2) |
其中,p为流场的压力,T为流场的温度,R为常数。因此,折射率可以看作压力和温度的函数。对其求导数,将得到:
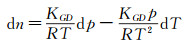
|
(3) |
表达式(3) 说明流场中的折射率变化随着压力和温度的变化而改变。考虑当细光束沿垂直壁面的方向穿过边界层的情况(或者细光束沿边界层外边界法向入射边界层的情况),在光束传播的方向上,边界层的压力特性是:
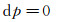
|
(4) |
将(4) 代入(3) 可以得到:
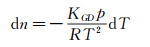
|
(5) |
式(5) 表明,沿边界层的法向,流场中的折射率变化趋势与温度场变化趋势相反。进一步引入牛顿关于热输运的方程:
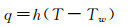
|
(6) |
其中,q是壁面热流,h是热交换系数,Tw是壁面温度。
在壁面处将式(6) 代入式(5) 可以得到:
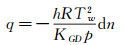
|
(7) |
这说明壁面热流与局部的折射率梯度成正比(变化趋势相反),即:
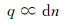
|
(8) |
另一方面,从气动光学角度考虑细光束的偏折角与折射率的关系,有如下公式:
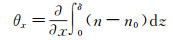
|
(9) |
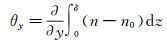
|
(10) |
其中,x代表流向,y代表展向,z代表垂直壁面的法向,δ为边界层厚度。在边界层内,公式(9) 和(10) 表明偏折角的各分量是折射率沿着光束传播方向求和后沿各方向的梯度。特别地,对于流向偏折角,〈θx〉反映了折射率在边界层法线方向上的总体变化,因为边界层的发展是流向Rex的函数,这正说明流向偏折角均方根是流向Rex的函数,即:
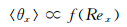
|
(11) |
从气动热的角度出发,壁面热流的流向分布同样随着边界层的发展而变化,因此,壁面热流同样是流向Rex的函数:
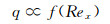
|
(12) |
综合上述分析,尤其是式(11) 和式(12),可得到结论:
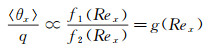
|
(13) |
对于公式(13),可以从气动热学和气动光学的角度综合分析。从气动热角度看,壁面热流是由边界层流场中的各尺度流动结构与固壁之间的对流传热决定的;从气动光学的角度看,细光束的偏折角是因为边界层流场中时空都不均匀的折射率分布导致,折射率分布与密度分布相关(由Gladstone-Dale公式决定),密度分布是由边界层流场中各尺度流动结构决定的,因此,细光束流向偏折角的统计量同样由边界层流场中的各尺度流动结构决定。特别地,对于高超声速边界层的转捩过程而言,热流沿流向的分布与流向偏折角统计量沿流向的分布之间的关系,可能存在着比公式(13) 更简单的关系,即两者可能存在某种线性比例关系,即:

|
(14) |
实验分测热实验与测光实验两个部分,均在中国航天空气动力技术研究院的FD-20风洞中完成,实验中,该风洞以炮风洞方式运行。实验Ma数为8,单位长度ReL数为1.0×107/m。实验模型为长459mm,宽300mm的平板,又分为测热和测光两块平板模型。测热平板模型的中心线上布置测热孔(距前缘80~340mm,使用薄膜电阻测热技术进行热流测量。测光平板模型沿流向布置了三个50mm×50mm的光学窗口,窗口中心位置分别距前缘为193mm、283mm、411mm。
光测实验使用了波长为632.8nm,功率为2mW,出射直径为1mm的氦氖激光器,采集系统使用了加拿大Mega Speed公司的一款黑白CMOS相机及相应的控制软件。相机芯片的最大分辨率为1280 × 1024像素,满分辨率时拍摄速度为1000fps,实验时选择分辨率为600 × 500像素,拍摄速度为2000fps,均由软件进行控制。实验采用了如图 1所示的光路。
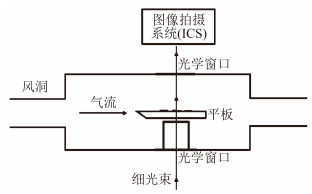
|
| 图 1 实验光路简图 Fig. 1 Sketch of the light in the experiments |
3 实验结果 3.1 热流分布
在平板上,高超声速边界层的转捩区域是随着ReL的变化而变化的。图 2给出了Ma=8,ReL=1×107 /m时的热流分布。在此条件下,沿着平板中心线,随着热流值的变化,可判断转捩发生在距前缘200~300mm的区间内。
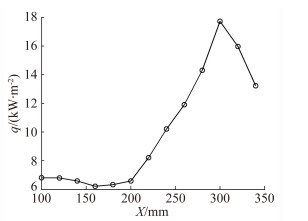
|
| 图 2 平板壁面中心线上的热流分布(Ma=8) Fig. 2 Heat transfer distribution at the centerline on the wall of the flat plate (Ma=8) |
3.2 光斑的抖动
细光束通过模型流场后,在高速摄像机芯片上成像为一个光斑。风洞运行时,因为模型流场的作用,光斑像会发生气动光学效应,产生偏折、模糊和抖动。利用高速摄像机,能够得到光斑的变化情况。图 3(a)给出了光斑在流场建立后某一时刻的图像。图 3(b)给出了经过34.5ms后的光斑位置,其中,红十字所处的位置是(a) 图中光斑的质心位置,可以从视觉上直观看出实验过程中光斑出现了位置上的偏移。

|
| 图 3 细光束成像光斑在不同时刻的位置对比 Fig. 3 Comparison of the location of the spot centroid at the different moments |
3.3 偏折角时间序列
细光束通过边界层流场后发生偏折,其偏折角的计算公式为[11]:
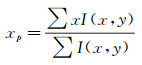
|
(15) |
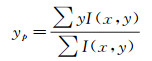
|
(16) |
其中,x,y是照片上的像素坐标,I是对应像素上的光强灰度,xp是光斑质心的横坐标,yp是光斑质心的纵坐标。由此计算偏折角的x分量θx和y分量θy:
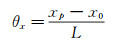
|
(17) |
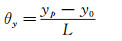
|
(18) |
其中,x0和y0分别是光斑初始状态时的横坐标和纵坐标。
根据上述公式,可以计算每幅照片里的光斑对应的偏折角,得到偏折角时间序列,如图 4(b)所示。图 4(a)给出了风洞运行时的总压曲线,将其与偏折角时间序列对比,可以确定有效的偏折角时间序列。图 4中蓝色方框所标记的区域,从总压曲线角度讲是流场建立的时间,从偏折角时间序列角度讲,是边界层流场形成并产生光学效应的时间。因此,有效的偏折角时间序列即可由此确定。
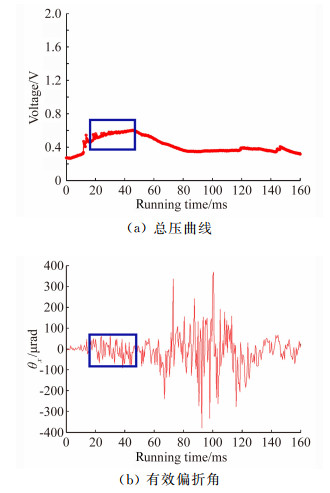
|
| 图 4 总压曲线与有效偏折角时间序列的选取 Fig. 4 Curve of total pressure and the selection of the effective deflection angle time series |
3.4 偏折角标准差的分布
在不同流向位置上选取对应的有效偏折角时间序列,进行统计计算,求出这段时间序列的标准差,可以得到偏折角标准差的流向分布,将这一分布与热流分布进行对比,如图 5所示。实心圆点曲线是热流曲线,由此曲线可以识别从200~300mm的转捩区。在这个区域内,空心圆点曲线代表的细光束偏折角标准差分布曲线具有同样的增长趋势。在转捩区域外,测量结果也有着相似的变化趋势。在200mm前的层流区,热流与光束偏折角标准差都变化不大,而在300mm后的湍流区,两者均表现出下降的趋势。
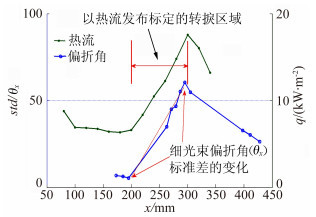
|
| 图 5 细光束偏折角标准差与热流分布的趋势对比 Fig. 5 Comparison of the heat transfer and the standard deviation of the deflection angle time series |
如果将公式(14) 与图 5中的两条曲线对比,可以计算得到const=5.0194μrad·m2/kW。
4 结论本文对边界层的气动光学效应问题进行了理论分析,具体处理了垂直边界层入射的细光束的流向偏折角问题,在流向偏折角统计量与壁面热流之间建立了联系(公式13),并针对高超声速边界层的转捩区中的上述联系进行了预测,提出两者存在线性比例关系的猜想(公式14)。
本文使用ICS技术和细光束技术,测量了激光细光束通过高超声速平板边界层流场时的抖动情况。这种抖动在层流至湍流的整个范围内都存在。层流、转捩过程中以及湍流三种流动状态的边界层对光束的抖动影响具有一定的演化趋势,这种趋势与边界层对壁面气动加热的性质,即热流分布,有同样的增长趋势,这验证了公式(13) 和(14) 给出的结果和猜测。
从公式13(或14) 可以看到,高超边界层的发展演化在形成气动热效应的同时也引起气动光学效应。这两种效应都是由于边界层内的不同尺度结构的发展演变和相互作用,以及流动结构与壁面的相互作用导致的。这就是说,如果我们能够从气动热角度对高超声速边界层的流动演化有更多认识,将推动对气动光学效应的认识,提升气动光学校正技术水平;另一方面,如果从气动光学角度了解更多光束传播的特性,也可推动对于高超声速边界层转捩测量技术的发展,甚至可以直接在细光束技术基础上发展出可应用于边界层转捩检测的光学方法。
致谢: 感谢甘才俊、史可天、潘宏禄、李烺等在相关问题上给予的讨论和帮助。| [1] |
Li G C.
The aero-optics[M]. Beijing: National Defense Industry Press, 2006.
(in Chinese) 李桂春. 气动光学[M]. 北京: 国防工业出版社, 2006. |
| [2] | Liepmann H W. Deflection and diffusion of a light ray passing through a boundary layer[R]. Report No. SM-14397, Douglas Aircraft Company, Santa Monica Division, California, 1952. |
| [3] | Sutton G W. Effect ofturbulent fluctuations in an optically active fluid medium[J]. AIAA Journal, 1969, 7(9):1737–1743. DOI:10.2514/3.5384 |
| [4] | Jumper E J, Fitzgerald E J. Recent advances in aero-optics[J]. Progress in Aerospace Science, 2001, 37:299–399. DOI:10.1016/S0376-0421(01)00008-2 |
| [5] | Jumper E J, Hugo R J. Quantification of aero-optical phase distortion using the small-aperture beam technique[J]. AIAA Journal, 1995, 33(11):2151–2157. DOI:10.2514/3.12960 |
| [6] | Gordeyev S, Jumper E J, Ng T T, et al. Aero-optical characteristics of compressible, subsonic turbulent boundary layers[R]. AIAA 2003-3606. |
| [7] | Gordeyev S, Jumper E J. The physics of boundary-layer aero-optic effects[R]. AFRL-OSR-VA-TR-2012-1152, 2012. |
| [8] | Wyckham C M, Zaidi S H, Miles R B, et al. Measurements of aero-optic distortion in transonic and hypersonic, turbulent boundary layers with gas injection[R]. AIAA 2005-4775. |
| [9] | Wyckham C M, Smits A J. Comparison of aero-optic distortion in hypersonic and transonic, turbulent boundary layers with gas injection[R]. AIAA 2006-3067. |
| [10] | Wyckham C M, Smits A J. Aero-optic distortion in transonic and hypersonic burbulent boundary layers[J]. AIAA Journal, 2009, 47(9):2158–2168. DOI:10.2514/1.41453 |
| [11] |
Yin X L.
The theorem of aero-optics[M]. Beijing: China Astronautics Press, 2003.
(in Chinese) 殷兴良主编. 气动光学原理[M]. 北京: 中国宇航出版社, 2003. |


