空中加油是指在飞行中由一架装载燃油的飞机,利用加油设备,给一架或者多架飞机加注燃油。通过空中加油,飞机的航程和作战半径加大了。一般地,轰炸机通过空中加油,作战半径可增加25%~30%,战斗机作战半径可增加30%~40%,运输机航程可增加一倍[1]。增大航程的作战飞机可以远距离迅速转移,实施突然袭击或战略布防。使用空中加油的飞机,可以最大限度的载弹或载货,仅对油箱进行部分加油,起飞后或飞行一段距离后再进行补充加油。这样既解决了油量少的问题,又降低了飞机起飞对机场跑道的使用要求,即飞机可以在不能承受很大单位载荷的软路面跑道上起飞。空中加油增加了续航时间的同时,大大减少了出动飞机的数量和使用强度,能在很大程度上缓解战争对空军、海军航空兵作战使用的需求和可能的矛盾。对舰载飞机来说,在舰面出现不能着舰的紧急情况时,可以对返航的飞机进行空中加油,使之留空待命或转飞备降机场。空中加油技术经过不断改进、提高,两种空中加油系统(硬式和软式) 日臻完善,为世界各国采用。目前,北约、英国、美国海军和其他国家都采用软式加油,硬式加油主要是美国空军采用。软式加油的特点是技术较简单,安全性较好,但加油量较小;硬式加油的特点是加油量较大,加油快,但技术要求高,安全性不如软式加油方式。现代加油机中软式加油方式更普遍些。
软管式空中加油技术是一种以“加油机被动,受油机主动”的对接加油技术,也是一种两机相连的超密集飞行,因此其间空气动力的相互干扰是不可避免的,并直接影响飞行安全。尤其发生在飞行包线边界附近和穿过云层等不利气象环境下,干扰现象明显加剧,甚至还可能引起电磁影响。因此仅按“稳态飞行”的空气动力分析是不够的。国内外对软式加油的流场研究及飞行试验日趋增多并取得了一定的成果[2-5]。Kapseong R.等人[6]用多体动力学理论建立加油软管的模型,将软管分段为刚性杆和集中质点系来研究软管的动态响应。Sriram V.等人[7-9]对受油机、加油机的相对运动和加油机尾涡诱导动态耦合作用进行了研究,建立了加油机尾涡作用模型。EichlerJ.[10]从作用在软管上的力平衡条件[11]出发,导出了加油软管的拖曳位置方程,并对加油机俯仰振荡和受阵风时软管的动态响应过程进行了模拟。胡孟权等人[12]考虑了大气紊流和加油机尾流场的扰动,根据空中加油软管、稳定伞的空间受力情况,建立了空中加油软管锥套动力学模型,仿真计算和分析了晴空大气紊流对空中加油软管锥套运动的影响。王伟等人[13]利用Matlab/Simulink仿真平台搭建加油软管-锥套系统的动态模型,对不同飞行条件下软管-锥套系统的软管位置、软管拉力进行了计算,对软管-锥套动态特性进行了分析。此外,关于加油对接过程中受油机的头波效应[14-16]的影响也有一定的研究,其研究结果对软管式空中加油的顺利对接具有一定的指导意义。
本文采用数值模拟的方法对在对接过程中加油锥套的运动进行了数值模拟研究,研究内容包含不同对接速度时加油锥套的运动情况,并形成规律,为这类飞机的空中加油提供气动方面的技术参考。
1 数值方法介绍数值方法包含三部分内容,一是非定常流动的数值模拟,其次是动网格技术,最后是软管锥套系统的动力学模型。
1.1 非定常流动数值模拟方法采用了雷诺平均N-S方程。紊流模型采用S-A一方程紊流模型[17]。本文所采用的计算软件经过多个算例验证,计算结果可靠合理。
三维可压雷诺平均Navier-Stokes方程为:
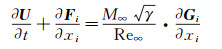
|
(1) |
其中,

|
(2) |
这里的ρ、p、e、T和k代表密度、压强、能量、温度和热传导系数,ui是沿直角坐标系xi方向的速度分量,σmi为黏性切应力的分量,M∞为来流马赫数,Re∞为来流的雷偌数。
空间离散采用了Osher格式[18];时间项采用隐式离散。离散后得到如下迭代方程:
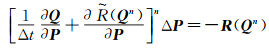
|
(5) |
其中n表示时间步,R是离散后的残值,P=(ρ, u, v, w, p) 是原始变量且满足Pn+1=Pn+nΔP。
1.2 动网格技术在模拟这类问题时,因有加油软管的柔性变形,同时锥套有大幅摆动,所以要求网格在每个周期结束后能回归到以前同样的网格。常用的基于弹簧准则的动弹网格技术因是通过迭代移动网格,周期结束后不可能恢复到周期前的网格状态,因此,采用作者提出的基于Delauney图的动弹网格技术[19]。该方法把对网格的移动转移到Delauney图的移动上,所有的对网格的扰动都转嫁到对Delauney图移动变形操作上。最后通过映射得到移动后的网格。该方法通过映射,能保证网格移动(变形) 前后的网格点分布密度、网格的拓扑结构得到保持,适合任意拓扑结构网格的移动变形。同时不需要叠代操作,因而该方法效率高。图 1是加油软管网格移动前后示意图。

|
| 图 1 加油软管网格移动前后示意图 Fig. 1 Hose mesh before and after movement |
1.3 软管系统动力学模型 1.3.1 模型假设与坐标系定义
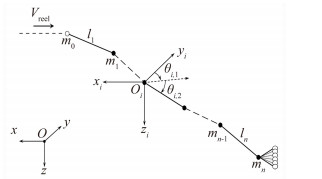
在忽略软管的轴向伸长和绕轴扭转情况下,采取如下方法对软管系统进行简化,如图 2所示,对于伸出加油吊舱的软管,可以将其离散成一段段无质量刚性杆,而杆与杆之间则由有质量的球铰连接起来,通过以上处理方法,软管系统便处理成一种开链式的多体系统。
|
| 图 2 软管多体系统模型及坐标系描述 Fig. 2 Demonstration for horse model and coordinates |
软管-锥套系统的运动由两类坐标系描述,第一类为全局参考坐标系Oxyz:x方向从机尾指向机头,y方向从左翼指向右翼,z符合右手定则;第二类坐标系为软管离散节点的连体坐标系Oxiyizi,其原点在对应节点中心,各轴的方向与全局参考坐标系保持一致。软管微段的位置采用二欧拉角θi, 1、θi, 2进行描述(由于忽略了软管的扭转效应,所以无第三欧拉角)。
为方便对软管系统进行描述,这里对软管各节点和微段进行编号,对于具有n个微段的加油软管,其节点编号从靠近加油吊舱点到与锥套连接点依次从0递增至n,并且将始末端之外的节点称之为常规节点,微段编号依次从1递增至n,对于微段,其长度由li表示。对任一节点i,其质量mi有如下关系:
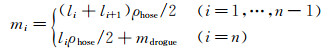
|
(6) |
式中,ρhose为软管的线密度,mdrogue为锥套的质量。
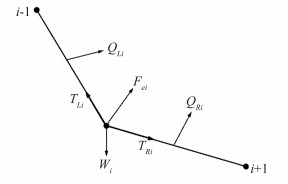
1.3.2 受力分析对任一节点i进行受力分析,如图 3所示,设气动力Qi作用于软管微段的中心,并可以通过受力等效到节点i上,软管微段之间的弯曲影响用等效恢复力Fi表示,记节点i的合外力为Hi,有:
|
| 图 3 节点i受力分析 Fig. 3 Force analysis for point i |
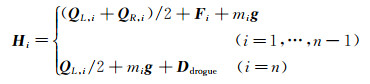
|
(7) |
式中,Ddrogue为锥套的阻力,由牛顿第二定律,节点i的加速度可以表示为:
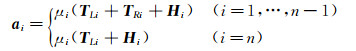
|
(8) |
式中,μi为节点i质量mi的倒数。
1.3.3 运动学方程由上述分析可得到软管微段的运动学方程[20]:
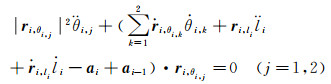
|
(9) |
其中ri是软管微段在坐标系Oxiyizi中的位置矢量。
对上式,若给定拖拽点的速度、加速度以及软管各节点的速度、加速度,则软管微段的方位角及其一阶导数可采用四阶经典Runge-Kutta方法进行时间推进。
1.3.4 动力学方程软管各节点的动力学方程[20]可表示为:
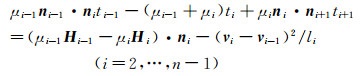
|
(10) |
ni为由节点i-1指向i的单位向量,ti为节点拉力大小。
记Ti=niti, 当边界条件(拖拽点,锥套连接点) 给定,软管各节点的动力学方程可写成矩阵形式,有:
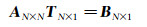
|
(11) |
显然,矩阵AN×N是一三对角阵,可采用追赶法对TN×1进行求解。
当与流场耦合计算时,获得流场信息后可计算出软管微段及锥套的受力,然后根据上述模型算出软管及锥套在一定时间间隔的位移量,并依据动网格方法及得到的位移量进行网格移动,进而进入新的流场计算循环中,具体步骤如下:
1) 求解N-S方程,获取流场;
2) 计算软管微段气动力(摩擦阻力、压差阻力),锥套阻力,软管节点恢复力;
3) 求解动力学方程,确定软管微段拉力;
4) 求解运动学方程,积分得到下一时间步软管微段方位角及其一阶导数;
5) 由软管方位角、方位角一阶导数,更新软管节点坐标、速度;
6) 若飞机移动距离小于设定距离,则重复步骤2)~5);若飞机移动距离达到设定值,求解完毕。
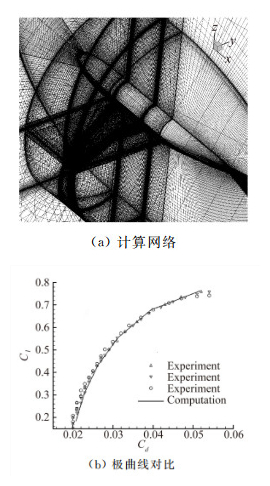
1.4 数值方法验证验证算例模型为DLR-F4,为AIAA第一届阻力系数预测研讨会所提供[21],其中计算网格和实验数据为波音公司所提供,约有350万网格点。计算马赫数为0.75, Re为3×106, 迎角分别为-3°,-2°,-1°,0°,1°,2°。图 4给出了计算结果和实验数据的比较示意图,从图中可以看到两者吻合得较好,反映出了本文所用CFD方法的合理性和准确性。
|
| 图 4 DLR-F4翼身组合体网格及极曲线 Fig. 4 Mesh and polar curve for DLR-F4 |
2 加油对接时锥套运动的数值模拟
在空中加油过程中,受油机的流场不但受到加油机机翼气流的强烈扰动,而且也受到加油锥套气流的扰动。当受油机接近锥套时,由于受油机的逼近所产生的前冲压力使锥套原有的平衡被破坏,产生摆动,两者相互作用加剧了锥套摆动和锥套尾流对受油机的影响,距离受油头越近,摆动量和摆动速度越大。空中加油有关对接加油的参数,如对接速度、锥套距受油头的三向距离、摆动量、摆动速度和旋转频率等。这些数据为飞行员再次飞行时纠正和改进飞行操作提供了依据,为飞行员控制两机的相对速度提供了依据。空中受油飞行试验结果表明:加/受油机在对接过程中,随着受油机向加油锥套的逐渐逼近,锥套受受油机前推气流的影响,产生远离受油机的逃逸(摆动) 现象是正常的。所以,加/受油机的对接过程应尽量短,并且应避免近距离的长时间占位,防止锥套受气流影响而引起不规则振荡。因此加油对接时,调整好两机的对接速度,飞行员保持平稳驾驶受油机,且受油头要对准加油锥套是确保成功对接加油的关键。
本文对某飞机加油过程中在不同对接速度下的锥套运动情况进行了数值模拟。计算网格总数为2400万左右,来流马赫数为0.65,加油飞行高度为5000m。计算采用并行计算技术,计算核数为48,计算边界采用无反射边界条件,残值以10-4为收敛标准。
数值模拟中采用的加油软管和锥套的参数及尺寸见表 1。
| 物理 参数 |
软管 总长 /m |
杨氏 模量 /MPa |
软管线 密度 /(kg·m-1) |
锥套 质量 /kg |
稳定伞 阻尼面积 /m2 |
| 24.0 | 8.0 | 4.2 | 30.0 | 0.204 |
为了方便,在实时显示过程中采取了锥套向受油机运动,在x方向其运动速度为对接速度。模拟的对接速度包含0.6m/s、1.2m/s、2.0m/s、3.0m/s。下面给出计算结果,其中X、Y、Z代表锥套的中心位置。
1) 0.6m/s:
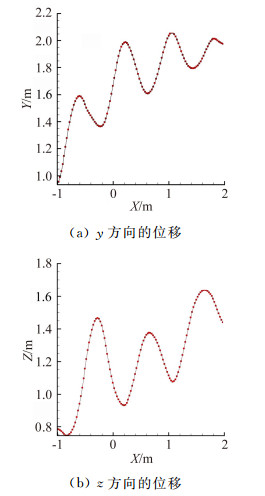
先计算对接速度为0.6m/s时的模拟结果。图 5给出了加油锥套的运动轨迹。
|
| 图 5 0.6m/s对接速度时加油锥套运动轨迹图 Fig. 5 Trajectory path of drogue at 0.6m/s |
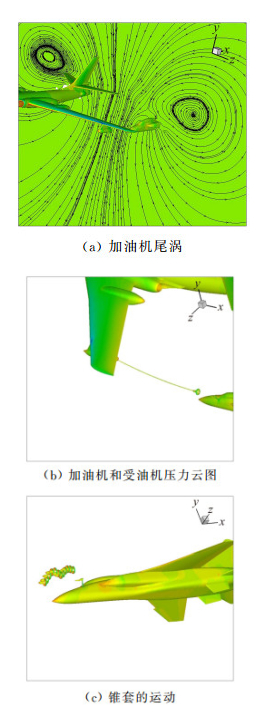
从上面的结果可知,当以0.6m/s速度进行对接时,加油锥套以近0.6Hz的振动频率进行摆动,同时向上向外移动,如图 6所示。
|
| 图 6 加油锥套模拟结果图 Fig. 6 Simulation results for the refueling drogue |
2) 1.2m/s:
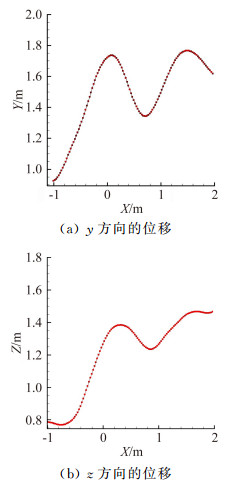
图 7给出了对接速度为1.2 m/s时加油锥套的运动轨迹。
|
| 图 7 1.2m/s对接速度时加油锥套运动轨迹图 Fig. 7 Trajectory path of drogue at 1.2m/s |
由图 7可知,对接速度为1.2m/s时,加油锥套仍然是以近0.6Hz的振动频率进行摆动,同样存在向上移动,因对接速度比加快了一倍,振荡周期由原来的三个减为两个,但因锥套有周期振荡,仍然存在加油对接困难的问题。
3) 2m/s:
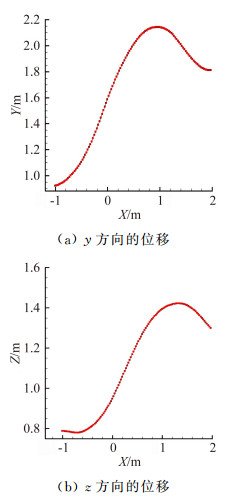
图 8给出了对接速度为2m/s时加油锥套的运动轨迹。
|
| 图 8 2m/s对接速度时加油锥套运动轨迹图 Fig. 8 Trajectory path of drogue at 2m/s |
从上面的结果可以看到,以2m/s速度进行对接时,加油锥套仍然是以近0.6Hz的振动频率进行摆动,同样存在向上移动,锥套也有一定的振荡,加油对接仍然具有一定的技术难点。
4) 3m/s:
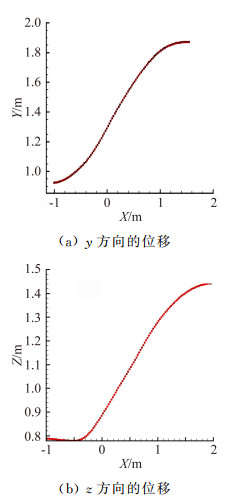
下面给出对接速度为3m/s时的模拟结果(图 9)。
|
| 图 9 3m/s对接速度时加油锥套运动轨迹图 Fig. 9 Trajectory path of drogue at 3m/s |
从图 9的结果可以看到,以3m/s速度进行对接时,加油锥套存在向上移动,飘移距离在0.8m左右,但周期性的振荡表现较小,这主要是因为对接速度大以后加油锥套的周期性振荡刚刚开始,尚未达到1/2个周期,这使得锥套表现出无振荡现象,因而从气动上来讲,以该速度或者大于该速度加油对接会容易得多,但当大于该速度时,在气动力作用下软管会出现上翻扬起现象,随之迫使受油插头出现突加弯矩而折断,因而在确定最终的加油对接速度时需要权衡多方面的因素。
从图 6可以看到,软管加上锥套其运动效果类似于单摆运动,从单摆的简单公式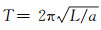
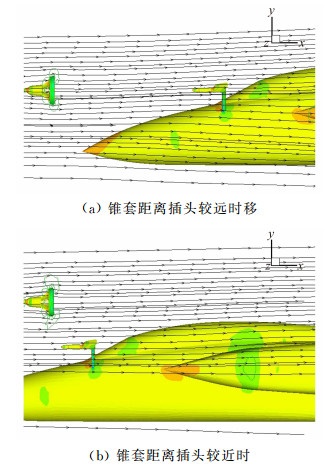
图 10给出了受油机向前对接时的流线及压力云图,其中图(a) 为飞机与锥套距离3m,图(b) 为距离0m。因锥套的稳定伞作用,在平衡位置时,锥套轴线方向始终与当地流场方向一致,而飞机靠近锥套时,因飞机机头的头波效应将改变当地流线方向,使得流线向机身外侧扩张,在飞机机头上方就表现出流线方向向上向外改变,锥套的平衡位置也将向上向外改变,这就使得锥套因平衡位置的变化出现摆动,并且总体趋势向上向外运动,这从前文所示的轨迹图中也反映了出来。当飞机以0.6m/s速度靠近时,因速度慢,锥套得以摆动三个周期,而靠近速度增大时摆动周期减少,如图 9所示,锥套摆动周期仅有1/2,直观反映为没有摆动直接向上向外运动。
|
| 图 10 飞机接近时流线及压力云图 Fig. 10 Streamlines and pressure contours |
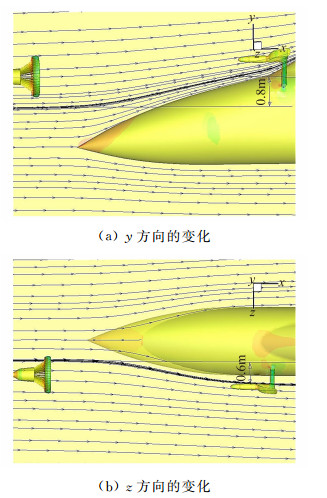
在锥套稳定伞的作用下,锥套轴线在平衡时总是顺着流线,因而可以通过判断流线在不同方向的落差大小来判断锥套平衡位置的移动情况。图 11显示了y、z方向的流线因受油机靠近而导致的向上、向外移动的情况,得到y方向变化量大致在0.8m (流线从锥套出发到受油头其y向距离变化情况),z方向变化量大致在0.6m (流线从锥套出发到受油头其z向距离变化情况),所以对上述任一对接速度,锥套飘移的平均距离大致相同,这在图 5~图 9中亦反映出来。
|
| 图 11 锥套平衡位置的移动情况 Fig. 11 Variation of equilibrium position of drogue |
当飞机以速度0.6m/s的相对速度靠近时,因飞机的靠近导致平衡位置发生改变,锥套开始运动,具有单摆运动的特性,又因靠近的速度较慢,锥套得以完成完整的单摆运动,且在经历相同时间内平衡位置的改变量较小,锥套振幅较小,这在图 6中直观地反映了出来。当飞机以较快的相对运动速度(1.2m/s) 靠近时,在经历相同时间内平衡位置改变量较大,振幅变大,并且锥套有完整的周期振荡,如图 7所示,该种情况不利于飞机的对接。当速度增加到3m/s时,因飞机运动速度较快导致锥套只完成1/2周期运动,锥套横向摆动速度小而易于飞机对接,并且从直观上看锥套只是向上向外运动,没有发生周期性摆动,从而易于飞机对接。
飞机以不同速度靠近锥套时,无论速度大小锥套平衡位置的变化很小,向上向外移动的总体距离大致相同,差别在于有不同的振荡情况,这从图 5-图 9中可以看到,因而在加油对接过程中速度较小引起加油锥套振荡,同时有向上向外移动,速度较大可以避免振荡,但易形成软管上翻扬起现象,随之迫使受油插头出现突加弯矩而折断。
3 结论本文采用数值模拟的方式对加/受油机在不同加油对接速度下的锥套运动轨迹进行了数值模拟,对接模拟速度从0.6m/s到3m/s。通过数值模拟,可以得到如下结论:
1) 在小速度的对接过程中,加油锥套呈现周期性振荡,但振幅较小。对接具有一定的难度;
2) 当加油对接速度达到一定程度后,加油锥套不再发生飘摆,但存在上飘的移动,这时加油对接要容易得多。
因对接接触瞬间引发的激励和伴随有空气动力的作用传递,以及随后的响应,使得输油软管产生互动耦合现象,即出现了向后推移的发散性横波振荡,直接引起受油插头承受巨大扭矩,因此,该课题的后期工作将结合结构动力学开展空中加油过程中出现的鞭打现象进行研究。
| [1] |
Xü G, Cao J Q. The status and development of overseas in-flight refueling technology[J].
Aeronautical Science and Technology, 1995, 1:27–30.
(in Chinese) 徐干, 曹近齐. 国外空中加油技术的现状及发展[J]. 航空科学技术, 1995, 1 : 27–30. |
| [2] | Vassberg J C, Yeh D T, Blair A J, et al. Dynamic characteristics of a KC-10 wing-pod refueling hose by numerical simulation[R]. AIAA 2002-2712. |
| [3] | Vassberg J C, Yeh D T, Blair A J, et al. Numerical simulation of KC-10 in-flight refueling hose-drogue dynamics with an approaching F/A-18D receiver aircraft[R]. AIAA 2005-4605. |
| [4] | Vassberg J C, Yeh D T, Blair A J, et al. Numerical simulations of KC-10 wing-mount aerial refueling hose-drogue dynamics with a reel take-up system[R]. AIAA 2003-3508. |
| [5] | Ribbens W B, Saggio F, Wierenga R, et al. Dynamic modeling of an aerial refueling hose & drogue system[R]. AIAA 2007-3802. |
| [6] | Ro K, Kamman J W. Modeling and simulation of hose-paradrogue aerial refueling systems[J]. Journal of Guidance, Control and Dynamics, 2010, 33(1):53–63. DOI:10.2514/1.45482 |
| [7] | Venkataramanan S, Dogan A. Dynamic effects of trailing vortex with turbulence & time-varying inertia in aerial refueling[R]. AIAA 2004-4945. |
| [8] | Venkataramanan S, Dogan A. Modeling of aerodynamic coupling between aircraft in close proximities[R]. AIAA 2004-5172. |
| [9] | Venkataramanan S, Dogan A, Blake W. Vortex effect modeling in aircraft formation flight[R]. AIAA 2003-5385. |
| [10] | Eichler J. Dynamic analysis of an in-fIight refueling system[J]. Journal of Aircraft, 1978, 15(5):311–318. DOI:10.2514/3.58361 |
| [11] | Hoerner S F. Fluid-dynamic drag[M]. Brick Town: Hoerner, 1965: 454-455. |
| [12] |
Hu M Q, Liu P, Nie X, et al. Influence of air turbulence on the movement of hose-drogue[J].
Flight Dynamics, 2010, 28(5):20–23.
(in Chinese) 胡孟权, 柳平, 聂鑫, 等. 大气紊流对空中加油软管锥套运动的影响[J]. 飞行力学, 2010, 28(5) : 20–23. |
| [13] |
Wang W, Liu X C, Wang P. Dynamics of hose-drogue refueling systems during coupling[J].
Flight Dynamics, 2013, 31(2):180–183.
(in Chinese) 王伟, 刘喜藏, 王鹏. 空中加油对接过程软管-锥套动态特性[J]. 飞行力学, 2013, 31(2) : 180–183. |
| [14] | Dogan A, Lewis T A, Blake W. Flight data analysis and simulation of wind effects during aerial refueling[J]. Journal of Aircraft, 2008, 45(6):2036–2048. DOI:10.2514/1.36797 |
| [15] | Dogan A, Blake W. Modeling of bow wave effect in aerial refueling[R]. AIAA 2010-7926. |
| [16] | Bhandari U, Thomas P R, Bullock S, et al. Bow wave effect in probe and drogue aerial refueling[R]. AIAA 2013-4695. |
| [17] | Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992. |
| [18] | Osher S, Solomon F. Upwind difference schemes for hyperbolic systems of conservation laws[J]. Mathematics of computation, 1982, 38(158):339–374. DOI:10.1090/S0025-5718-1982-0645656-0 |
| [19] | Liu X Q, Qin N, Xia H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2):405–423. DOI:10.1016/j.jcp.2005.05.025 |
| [20] |
Chen L L, Liu X Q, Wu C L. Dynamic characteristics research for variable damping paradrogue[J].
Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(4):607–612.
(in Chinese) 陈乐乐, 刘学强, 吴成林. 稳定伞变阻尼过程动态特性研究[J]. 南京航空航天大学学报, 2015, 47(4) : 607–612. |
| [21] | Redeker G. DLR-F4 wing-body configuration, a selection of experimental test cases for the validation of CFD codes[R]. AGARD AR-303, 1994. |


