2. 中国空气动力研究与发展中心, 空气动力学国家重点实验室, 四川 绵阳 621000
2. State Key Laboratory of Aerodynamics of China Aerodynamics Research and Development Center, Mianyang 621000, China
以X37B构型为代表的高升阻比复杂外形飞行器,再入和滑翔飞行高度一般定为30~70km之间,飞行马赫数变化范围为10~20,在整个飞行过程中,飞行器将经历一系列复杂的飞行环境。为实现远距离滑翔飞行,这类飞行器的气动外形设计比较复杂,除采用翼身融合布局外,还含有多种操纵舵面和RCS控制单元,几何上具有多尺度特征,如头部、翼/舵前缘、缝隙等特征尺度可能为毫米~厘米量级,而飞行器的长度、高度和翼展为米量级。在50km附近的高空进行高超声速飞行时,由于其周围的空气相对稀薄,因此,在这些小尺度结构附近的流动可能存在稀薄气体效应;在飞行器以较大迎角作高速飞行时,迎风侧的空气将受到显著的压缩,形成强激波,从而激发空气分子的内部自由度,出现复杂的物理化学反应,即真实气体现象;在高空由于空气密度比较低,尽管飞行马赫数比较高,但流动雷诺数仍然较低,黏性效应十分显著,出现不可忽略的黏性干扰现象。另外,由于这些现象往往都是同时发生,在实际流动中通常难以区分,而且多种效应耦合在一起对飞行器流动及其气动性能产生的影响,通常十分复杂。因此,开展高超声速飞行器流场中多物理效应的相互耦合作用的研究,不仅是高超声速空气动力学学科发展的需要,也是高超声速飞行器气动设计的需要,具有十分重要的学术价值和工程实用意义。
美国航天飞机是20世纪70年代研制的复杂升力体外形,飞行范围广,参数变化大,飞行马赫数0~30,再入迎角0°~40°以上,飞行高度0~500km,飞行雷诺数104~108量级,黏性干扰参数0.001~10,努森数0.001~几十,跨越了连续流区、过渡流区和自由分子流区,其高超声速流动特性包含了真实气体效应、稀薄气体效应、黏性干扰效应等多种物理效应。另外,有众所周知的ADDB (Aerodynamic Design Data Book) 气动特性数据库,可以作为数值模拟结果正确性判断的依据,能够为数值模拟研究提供有力支撑。最后,尽管有大量的研究工作,涉及真实气体效应等复杂物理效应对其高超声速气动力特性的影响,但这些物理效应之间相互耦合作用的研究工作涉及不多,有待于进一步深化。因此,我们选择美国OV102航天飞机为研究对象,采用数值模拟手段来开展复杂升力体外形高超声速流动多物理效应对气动力影响的研究工作。
在开展数值模拟研究工作之前,对美国航天飞机高超声速气动力的情况进行梳理和回顾是十分有必要的,这能为我们的研究工作提供指导和基础。60年代末,为了减少一次性使用的运载火箭的费用,美国国家航空航天局(NASA) 对可重复使用于近地轨道的飞行器的可行性进行过研究。1972年3月,NASA正式提出设计和研制轨道器的要求,根据研制的需要,随后成立了风洞试验协调小组。在协调小组工作期间(1972.9~1976.9),共举行了12次会议,1972年10月底举行的第一次会议决定了建立航天飞机气动设计数据库(ADDB),1973年11月举行的第五次会议上,决定将轨道飞行器2#(OV-102) 用于轨道飞行试验(OFT) 计划。航天飞机高超声速气动力研究主要依托风洞试验,并辅以理论分析方法,形成ADDB数据手册,最后通过飞行试验,验证和完善地面预测的气动力特性。本文将根据飞行前和飞行后两个阶段进行简单介绍。
1 飞行试验前的气动力特性研究在航天飞机的最初发展计划期间,为了加快研究进度,决定同时进行飞行控制系统(FCS) 的设计和验证性气动力风洞试验。在气动力验证过程中,预测的气动力特性很可能会变化,FCS设计必须具有对气动力特性的变化有一定的容忍度,因而要求空气动力学家们提供飞行前气动特性的不确定度。由此可知,飞行试验前的气动力特性研究包括气动力特性预测及其不确定度估计两个部分。
为研制航天飞机,完成了当时有历以来最大的一项风洞试验计划。为确定轨道器(图 1) 的气动性能、稳定性和控制特性,对它单独进行了超过27 000小时风洞占用时间的试验[1]。这些庞大风洞试验计划对气动设计数据手册(ADDB) 的组成和建立提供了基础,ADDB是主要承包商和NASA的几个研究中心共同努力的结果,它由一组数字化的表组成,这些数字是通过对所有有效试验数据的工程分析和修正研究得到的,根据经验和理论数据进行补充完善,并外推到飞行条件。因此,ADDB代表了飞行前气动特性的“最佳估算”。在马赫数低于15的情况,模型缩比选用传统的自由流雷诺数,由于试验设备能够在较大的马赫数范围内提供接近飞行条件的雷诺数模拟,因而不要求对风洞试验结果进行修正。在马赫数15以上的稀薄大气层内,由于同时存在黏性干扰效应、稀薄气体效应和真实气体效应等多物理效应,因而,传统的自由流雷诺数无法作为此种流动条件下关联气动特性的参数,为此,专门成立了一个研究小组,试图来解决此问题。

|
| 图 1 航天飞机轨道器布局 Fig. 1 Shuttle orbiter geometry |
1.1 气动力特性外推参数研究[2]
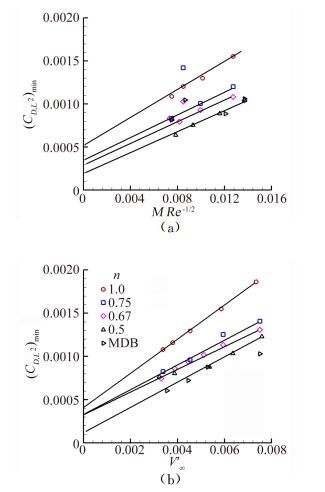
研究人员希望通过计算简单外形得到的真实气体效应数据和复杂外形的理想气体地面设备试验数据,关联得到真实气体效应对复杂外形气动力特性影响的认识。NASA和美国空军对不同类型的再入外形(按配平的升阻比分类) 进行试验,研究较大马赫数和雷诺数范围的气动特性的关联方法,以建立将地面设备数据外推到飞行条件的方法。如:Whitfield和Griffith研究了黏性阻力对钝头细长锥体的影响之后,主张利用Tsien的“滑移参数”V~MRe-1/2来关联黏性阻力和升阻比,他们也许注意到了与Lee和Probstein的高超声速黏性干扰参数(χ~M3Re-1/2) 的相似性,也将V称为高超声速黏性参数。关于黏性干扰系数的主要研究成果,大致有:(1) 对于尖锥给出了所谓的第一黏性干扰参数χc=Mc3[CRec-1]1/2(C=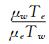

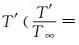
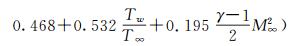
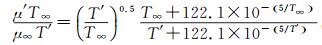
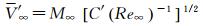
图 2给出了一系列n幂旋成体(半径=长度n) 和经典的最小阻力体(MDB) 的阻力结果与V∞和V′∞的曲线[2],空心旗标符号为M=10.3时空气流动的实验结果,空心符号为M≈20时氦气流动的实验结果,实心符号为V∞=V′∞=0时的非黏性理论计算结果。显然,V′∞能够很好地使数据相关起来;但V∞没有能够把这些数据很好关联起来,这是因为:对于空气数据,Chapman-Rubesin黏性系数C′∞≈1,V′∞≈0.008≈MRe-1/2,而当考虑包括不同试验气体以及宽广的飞行条件时,C′∞≈1不成立[2]。
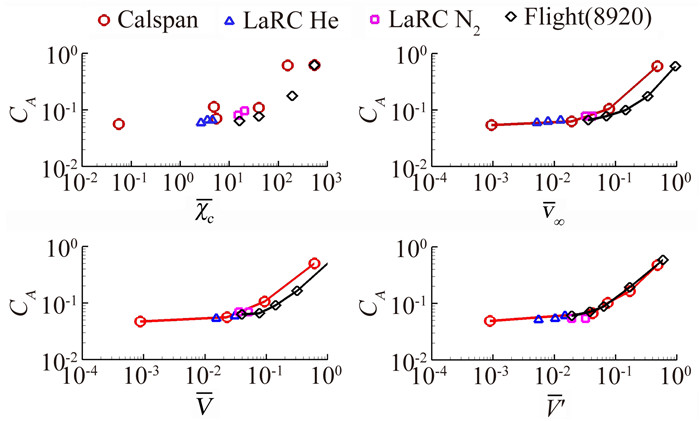
图 3为α=30°时高超声速风洞中航天飞机轨道器轴向力系数与4个关联参数的曲线图[2]。轨道器轴向力系数是基于15°锥采用Probstein的弱干扰理论估算得到的,计算的来流条件为M∞=8~30、Re∞, ι=0.001×106~6.8×106、γ=1.4和1.667,这既是进行航天飞机轨道器试验的高马赫数研究设备(卡尔斯潘风洞;兰利研究中心风洞M=19,氮气;兰利研究中心风洞M=20,氦气) 中的典型条件,也正是当时飞行设计弹道(8922) 中的典型条件。参数V′∞能够将地面设备和再入条件(理想气体) 下的研究结果全部关联起来,似乎具有将风洞条件和飞行条件下的高超声速数据相关起来的潜力。
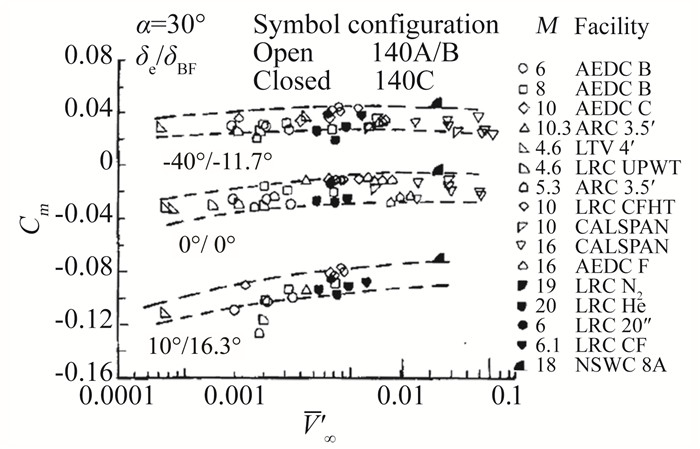
在上面研究成果的基础上,利用多个轨道器外形的试验模型、12座高超声速风洞和四种试验气体(空气、氮气、氦气和四氟甲烷(CF4)) 开展了试验研究[1],采用不同试验气体的目的是保证流动介质的比热比涵盖高超声速飞行过程中高温空气比热比的变化范围,期望模拟出真实气体效应对气动力特性的影响规律。对于升降舵和体襟翼偏角为δe/δBF=-40°/-11.7°、0°/0°和10°/16.3°的情况,在α=20°、30°和40°条件下纵向气动特性试验数据与V′∞进行关联。轴向力系数在绝大多数情况下,数据散布带宽约为±0.005,例外的情况(如α=40°和δe/δBF=10°/16.3°时) 为±0.01,随V′∞的增加轴向力系数增大,具有明确的关联特性,这验证了图 3所示的研究结论,与这些黏性干扰效应的影响相比,比热比(对于氦气,γ=1.667;对于空气和氮气,γ=1.4;对于CF4,γ=1.12,) 对CA的影响可以忽略;法向力系数和俯仰力矩随V′∞的变化不明显,表明它们同V′∞和γ的关联性不强,其中法向力系数的数据散布带宽保持在±0.03范围内,俯仰力矩系数的数据散布带宽为±0.003~±0.01。图 4为俯仰力矩系数随V′∞的变化曲线,图中空心符号代表0.010缩比和0.015缩比的140A/B轨道器模型的数据,实心符号代表0.004缩比的140C轨道器模型的数据。图 5为将各种数据叠加起来的关联曲线,总的来看,数据散布似乎均落在上面所介绍的界限内。地面风洞试验中气体比热比γ的变化范围为1.667→1.12,超过了实际飞行过程中γ的变化范围,试验数据因比热比的变化仍保持在总的散布带宽内,似乎有理由推断,真实气体效应的影响实际上可以通过风洞试验获得的气动力特性不确定度考虑进来。
为了解无粘真实气体效应对类似航天飞机这种布局的影响,还利用当时最先进的CFD代码(STEIN),对α=25°时修形140C航天飞机轨道器(机翼后掠角增加至55°,消除靠近翼梢的亚声速流动,保证空间推进方法的适用条件) 完成了三个状态的计算(两个理想气体条件和高度为240 000ft的一个平衡空气真实气体条件)。表 1为三个状态的气动力系数,M=10.3时,理想空气风洞条件与平衡空气再入条件之间的不同,使得升力系数减小10%的量级,轴向力系数没有明显变化,而抬头力矩增加了0.023。
总之,研究人员认识到改变比热比是当时唯一可用的研究真实气体效应的试验手段,综合运用当时的理论分析和试验手段,并没有解决任何关联真实气体效应对轨道器气动特性影响的问题,得到的阶段性结论是:比热比的变化引起的气动特性变化在风洞数据库的散布范围内,高空高马赫数飞行区域的气动力应该利用V′∞进行关联。由此可知,对于数值分析得到的真实气体效应对俯仰力矩的这种明显改变,当时并没有引起足够的重视,以至去重新审查风洞试验数据(后来的试验发现比热比的改变,同样会有大致0.03的抬头力矩产生[3-4]),也没有评估这样一个改变量会导致配平舵偏角产生多大的变化,显然,正是这种漠视为飞行试验中纵向配平出现异常埋下了祸根!
1.2 气动力的不确定度研究[1]飞行前气动特性的不确定度研究包含两个方面的内容。一是不同风洞试验之间气动力结果的差异估计,是飞行前气动特性最小误差的预测,称为公差(tolerance),公差是飞行控制设计中所采用的不确定度。一是飞行前气动力预测与飞行结果之间的偏差估算。估算的误差一定不能大到使飞行控制设计完全失效,由此得到一组“最坏情况”的气动力不确定度,定义为变差(variations)。在航天飞机飞行试验中所指的气动力异常,就是飞行试验得到的气动力特性与飞行前预测的气动力特性的差异超过了ADDB数据库中给定的变差。
公差的确定方法包括两步,第一步是:用各种不同的试验设备、不同的模型以及不同的试验团队,完成重复性试验,得到重复性偏差。第二步,基于风洞试验结果的重复性偏差和风洞结果与ADDB之间的差异,通过光滑得到每个马赫数数下的气动力公差。
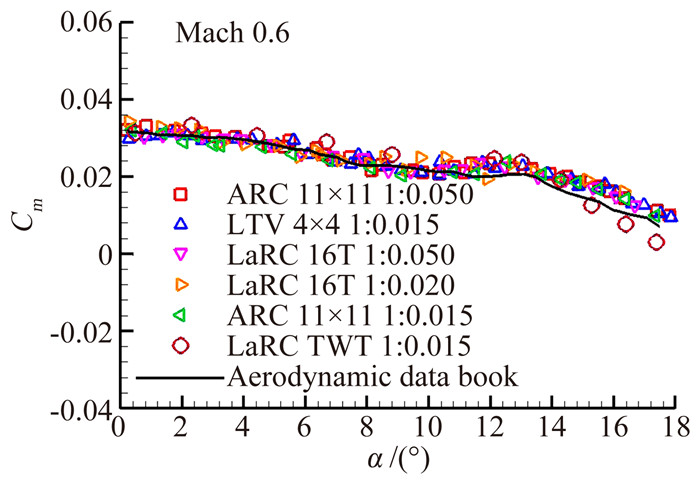
以下给出俯仰力矩系数公差确定的一个实例。图 6为马赫数0.6时俯仰力矩系数随迎角的变化曲线[1],包含了各种重复试验结果与ADDB的估算结果。重复试验包括:(1) 编号为39-0的模型(缩比为0.05),在ARC的11×11英尺设备和LaRC的16英尺跨声速设备中进行试验;(2) 编号为44-0的模型(缩比为0.015),在LTV的4×4英尺设备、LaRC的8英尺风洞和ARC的11×11设备中进行试验;(3) 编号为105-0的模型(缩比为0.02),在LaRC的16T风洞中进行试验。根据这些试验数据,确定俯仰力矩Cm的峰值-峰值重复性差异约为0.006。此重复性差异代表下列误差源的综合影响:(1) 几座风洞中采用相同的模型(风洞-风洞之间的重复性);(2) 同一风洞中采用不同的模型(模型-模型之间的重复性);(3) 不同的试验团队(试验技术差异),其中还包括任何雷诺数效应和堵塞效应。
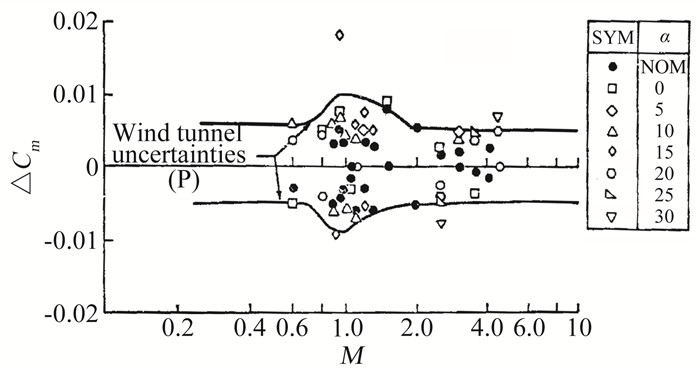
根据这种基本曲线,将各种不同迎角下的风洞结果与ADDB之间的差异绘制成与马赫数之间的关系曲线,如图 7所示[1]。通过用工程判断的方法把穿过这些数据点的曲线进行光滑,得到公差(风洞不确定度)。在光滑处理过程中,给相应马赫数时弹道点上名义迎角上的变差以较高的权重。
确定变差最合理的方法,自然是从分析过去的飞机风洞试验与飞行试验之间的差异入手,用来进行与风洞试验比较的飞行数据,要求相应的飞行器与航天飞机轨道器之间具有几何相似性。与确定公差方法类似,将气动特性的飞行值与预测值之间的差异画成随马赫数变化的曲线,通过对曲线进行光滑来确定偏差。布局选择和光滑处理事实上存在一些主观性,为此专门成立了一个空气动力学家小组。
图 8为这个小组进行的飞行-预测相关性研究后建议采用的俯仰力矩Cm的偏差随马赫数的变化曲线[1]。正如从相关性分析图中能够看到的那样,所有飞行数据仅限于低超声速。在得不到飞行数据的马赫数区域,把公差乘以一个安全因子得到变差,安全因子通常取1.5。
2 飞行试验后高超声速气动力特性研究
在航天飞机轨道器再入过程中,为了获得气动力数据,专门设计了三类机动动作:(1) 拉起/下压机动(Pullup/Pushover) 动作,获得随迎角而变的纵向性能数据,(2) 机身襟翼偏转,获得机身襟翼效率,(3) 纵向和横向控制脉冲,获得稳定性导数和控制导数。总的来看,从前5次再入飞行中成功地获得了气动力性能和稳定性数据,在飞行结果与轨道器预测数据库之间具有良好的一致性,但也确实存在一些不可忽略的差异[5-10],这为飞行试验后轨道器高超声速气动力特性研究指明了方向。
2.1 飞行试验气动力特性与飞行前预测数据的比较为了科学地比较飞行前预测值与飞行数据,首先,了解它们各自的特征是非常重要的。飞行前预测值是基于风洞试验,风洞试验中的独立参数(包括来流压力、速度等自由流和迎角等姿态参数) 是确切知道的,而气动特性的精确度可能有问题;飞行试验中,气动特性可以确切地知道,而独立参数的精确度可能成为问题。因此,选择升阻比和压心位置(因为它们与动压(V) 无关),可以使独立飞行参数的误差影响减至最小,有利于为飞行前数据预测精度的分析减少不确定因素。
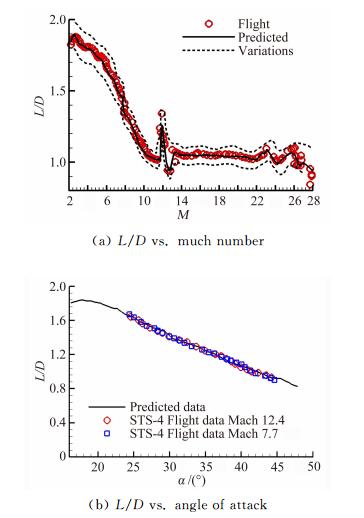
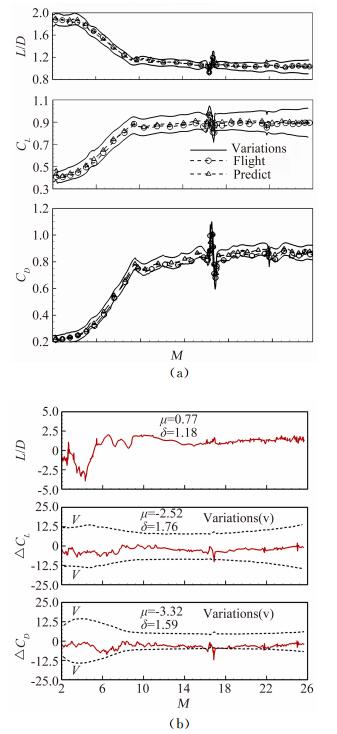
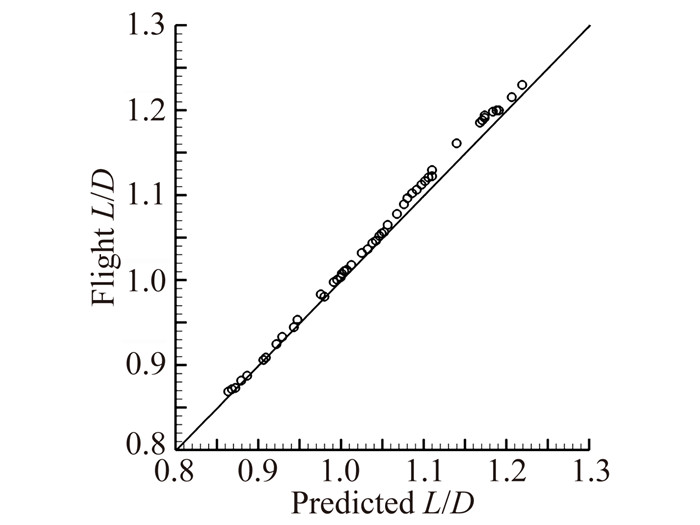
图 9为轨道器STS-4沿飞行弹道和拉起/下压机动飞行过程(唯一的运动控制面是升降副翼) 中升阻比,分别给出了升阻比随马赫数、升阻比随迎角变化曲线,飞行前预测值与飞行数据具有良好的一致性[5, 8],几次机动飞行,预测偏差大约为10%。
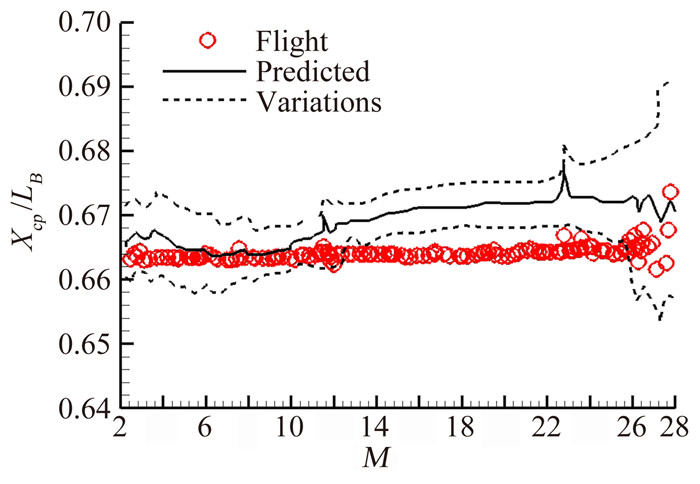
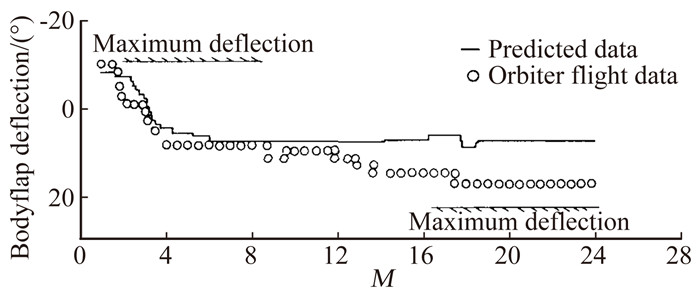
纵向气动力压力中心(XCP/LB) 也与动压无关,选用它来进行配平特性的比较。对于配平的飞行器,纵向压力中心(飞行器上俯仰力矩为零的假设点) 与重心相同。图 10给出了STS-4压力中心的飞行值与预测值的比较[5]。在M数大于10时,预测出的压力中心比飞行数据要靠后0.7%个机身参考长度(1.9%个平均气动力弦),图 11在STS-1的飞行过程中机身襟翼配平偏角随马赫数的变化曲线[6],在M数大于17时实际配平机身襟翼是16°而不是ADDB中预测给出的7°。轨道器的所有5次再入飞行的结果均是如此,由此可见,高超声速M数范围内的纵向配平有相当大的误差,而且超出飞行前预测值不确定度的范围。
现在来看看力系数的预测精度。图 12是M数为7.7和12.4条件下行机动飞行的轴向力和法向力系数随迎角的变化曲线[8],法向力系数(CN) 预测值要大于飞行结果,而轴向力系数(CA) 非常小,由此可知,高超声速时升力系数和阻力系数的飞行试验数据比预测值要小。
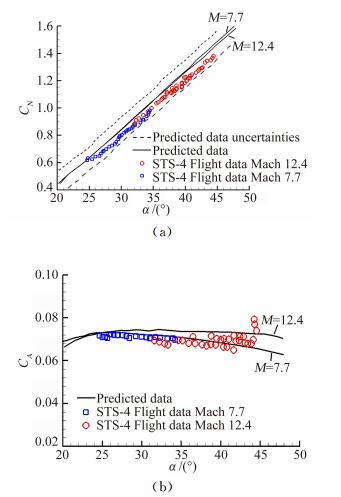
|
| 图 12 STS-4纵向气动力与预测值的比较[23] Fig. 12 STS-4 longitudinal aerodynamics comparison with preflight predictions |
在M=2~26的整个飞行范围内,通过统计得到了飞行值和数据手册值之间差异的平均偏差(μ) 和标准偏差(σ),升力系数CL和阻力系数CD的平均差异分别为-4.50±4.38%和-5.24±4.55%[14]。在M=20时的飞行高度范围(80 kft<h<220 kft) 内,计算出的CL和CD的平均差异分别为-3.3±2.5%和-3.7±2.4%。图 13为STS-5的升力与阻力与飞行前预测值的比较,除ΔL/D曲线外,还给出了数据手册中的气动力特性变差[9]。
表 2中列出了这些统计数据[9],还给出了每次飞行的高超声速范围内的平均偏差和标准偏差,以及相应的总平均偏差和标准偏差。L/D之差的平均偏差都是0.69±1.24%。在M数大于6时,平均偏差和标准偏差分别为1.16%和0.51%,由此判断,L/D的总偏差一般在2%以内。
| EVEN | ΔCL | ΔCD | ΔL/D | |||
| μ | σ | μ | σ | μ | σ | |
| STS1 | ||||||
| MACH 2-26 | -5.94 | 3.34 | -6.46 | 3.36 | 0.48 | 1.08 |
| MACH 6-26 | -5.85 | 3.62 | -6.72 | 3.51 | 0.82 | 0.56 |
| STS2 | ||||||
| MACH 2-26 | -6.86 | 6.45 | -7.60 | 7.03 | 0.65 | 1.29 |
| MACH 6-26 | -8.10 | 6.53 | -9.37 | 6.64 | 1.15 | 0.45 |
| STS3 | ||||||
| MACH 2-26 | -2.66 | 2.10 | -3.59 | 1.94 | 0.90 | 1.29 |
| MACH 6-26 | -2.42 | 1.69 | -3.83 | 1.76 | 1.36 | 0.45 |
| STS4 | ||||||
| MACH 2-26 | -4.24 | 4.32 | -4.97 | 4.56 | 0.68 | 1.31 |
| MACH 6-26 | -4.09 | 4.78 | -5.37 | 5.00 | 1.21 | 0.51 |
| STS5 | ||||||
| MACH 2-26 | -2.52 | 1.76 | -3.32 | 1.59 | 0.77 | 1.18 |
| MACH 6-26 | -2.11 | 1.58 | -3.41 | 1.52 | 1.25 | 0.38 |
| STS1-5 | ||||||
| MACH 2-26 | -4.5 | 4.38 | -5.24 | 4.55 | 0.69 | 1.24 |
| MACH 6-26 | -4.61 | 4.73 | -5.83 | 4.74 | 1.16 | 0.51 |
| μ=mean, % σ=standard deviation, % | ||||||
飞行过程中从脉冲机动获得的横向导数包括侧滑引起的偏航力矩导数Cnβ和滚转力矩导数Clβ、副翼效率导数Clδa和Cnδa结果,同飞行前预测值也有良好的精度,限于篇幅,不再展开。总之,在高超声速范围内,气动力特性的预测精度整体良好,但在M数大于10后,对纵向配平的预测结果存在较大的差距。
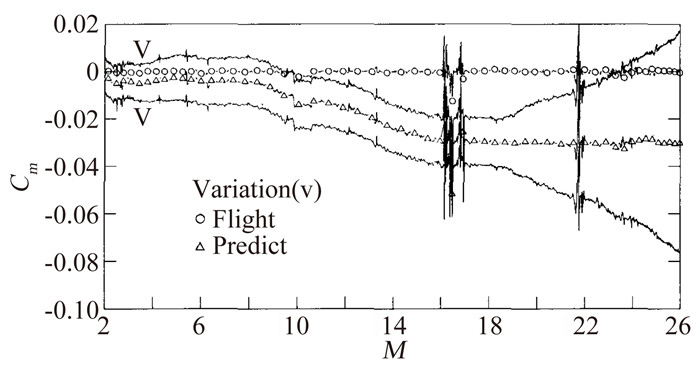
2.2 纵向配平特性异常分析图 14为基于飞行器重心的STS-5中Cm随马赫数而变的曲线[9],所有5次飞行与预测值的比较均是如此。在马赫数约为16~26之间,俯仰力矩差异最大,通常保持在0.03(在STS-2和STS-3中为0.035) 左右。这种差异,马赫数在16~8之间是随马赫数减小而减小,在8~2之间,几乎不随马赫数变化,保持在0.002左右。显然,如果把飞行前计算结果中真实气体效应对力矩的影响(0.023) 考虑到飞行前预测结果中,无论是加到预测值上,还是变差中,飞行数据就可能不会超出飞行前给出的变差线。
人们最早推断产生这种差异原因有[2]:(1) 体襟翼效率的预测误差;(2) 质心位置的不确定性;(3) 真实气体效应;(4) 基本构型(飞行器舵面偏角为0°) 的俯仰力矩cm0预测误差。除了第(3) 项是从流动现象上找原因外,其余均是从部件上的力矩来分析误差原因。
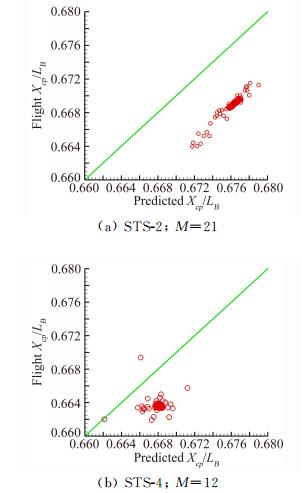
为了考察在真实飞行中的舵面效率与飞行前预测值的差异,在STS-2和STS-4中,加入机动飞行动作。从拉起-下压(pullup/pushover) 机动飞行可得出XCP/LB的相关性(图 15),STS-2在M=21时的数据具有非常好的直线相关性,它与理想的相关性直线平行,但有大约0.0075的偏差,而STS-4在M=12时的数据显示出大约0.004的偏差。由此可知,迎角效应和升降副翼效率与预测的一样,其偏差很可能是由于没有正确预测的飞行器基本俯仰力矩或低估机身襟翼效率约50%造成的[9]。
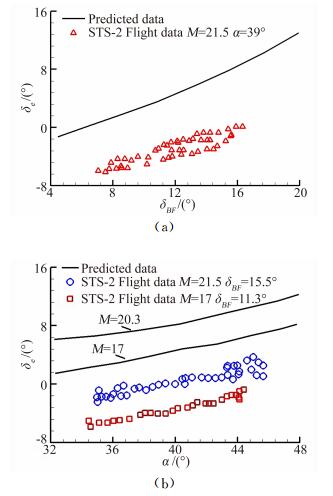
图 16分别为M=21.5时在机身襟翼正向偏转过程中获得的配平数据和在M=20.3和17.0时POPU机动飞行中获得的配平升降舵数据[8]。这些曲线的斜率表明,升降舵效率/俯仰静稳定性与预测结果很接近。由此推断,在高超声速条件下,纵向配平的预测误差的可归因于基本俯仰力矩(Cm0) 的误差。
为了分析航天飞机的纵向配平异常的流动机理,Maus等[11-12]人最早采用数值模拟手段,通过航天飞机的简化外形,采用平衡气体物理模型,对高空高马赫数条件下的流动进行了真实气体效应对气动力特性影响的研究,他们的结果表明,在飞行条件下,真实气体效应和马赫数效应对Cm0的影响大约为0.022(同飞行前特别小组的研究结果一致)。利用马赫数效应和真实气体效应修正Cm0的风洞值,给出在大迎角下配平航天飞行器所需的机身襟翼偏转角,其结果与飞行得到的机身襟翼偏转角一致,相差在2°以内。因此,似乎真实气体效应和马赫数效应是造成预测的配平特性与飞行数据差异异常的主要原因。但是,应该注意,图 15所示在高马赫数下俯仰力矩的差异大约为0.03,比真实气体效应和马赫效应的影响大30%左右。由于当时的计算机资源和CFD模拟软件能力的限制,无法明确给出造成的这30%左右的原因。
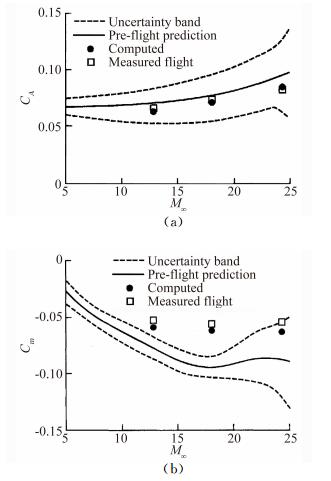
直到20世纪90年代初,Weilmuenster等[2-3, 13]针对完整的航天飞机轨道器外形,综合运用风洞试验和数值模方法,系统地考察马赫数、雷诺数、黏性干扰和真实气体效应对基本构形俯仰力矩和体襟翼效率的影响。风洞试验研究中,采用兰利研究中心的5座高超声速风洞,其中三座空气风洞(15英寸马赫6高温空气风洞、20英寸马赫6和31英寸马赫10) 和22英寸马赫20氦气风洞用来研究马赫6~20条件下的完全气体气动力,而20英寸马赫6四氟甲烷(CF4) 风洞用来研究真实气体效应,因为CF4具有真实气体较高密度比和较低比热比的特性。数值计算研究中,采用了LAURA程序求解薄层NS方程和7组分高温空气化学动力学模型。所得数值模拟结果与飞行结果比较,气动力差异在5%以内,体襟翼配平偏角在10%以内,图 17给出了轴向力系数和俯仰力矩系数[3],如果采用计算结果作为飞行前的预测值,就不会发生纵向配平异常的问题。另外,他们的研究结果还表明,真实飞行中质心位置的不确定性可能会导致体襟翼配平偏角有0.6°的差异,不是纵向配平异常的根本原因。需要特别强调的是,真实飞行条件下体襟翼效率的数值模拟结果是地面预测值的1.5倍,如果其效率与地面一致,则飞行时将无法在40°迎角时纵向配平[2],这与飞行试验结果给出的舵面效率分析结论不一致。
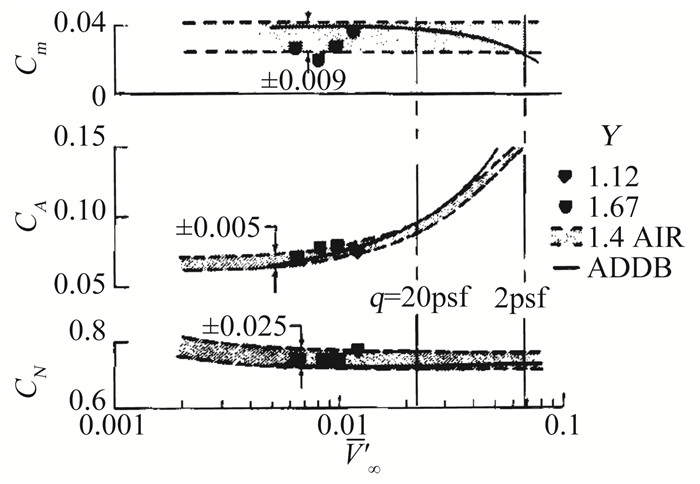
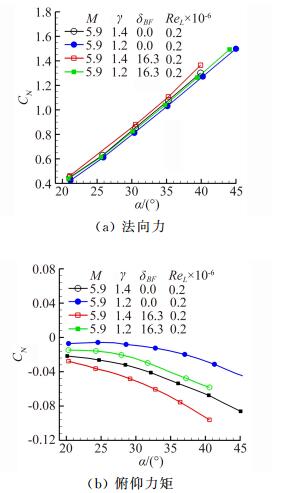
而风洞试验结果表明:20英寸马赫6四氟甲烷(CF4) 风洞试验比较好地模拟了航天飞机再入大气飞行过程中的真实气体效应的影响,所测得的气动力增量和体襟翼效率与飞行数据一致性良好。图 18给出了空气风洞和四氟甲烷风洞试验测量的法向力和俯仰力矩系数,四氟甲烷(低比热比/重气体) 风洞中的法向力系数要小,并出现了抬头力矩增量,马赫数6、迎角40°和雷诺数2×105条件下,δBF=0时,δCN=0.046,δCM=0.029,δBF=16.3°时,δCN=0.077,δCM=0.027,法向力系数的改变量同数值模拟结果一致,但俯仰力矩的改变量似乎受体襟翼偏转的影响不大,都很接近0.03。这里需要特别强调的是,飞行前也完成了类似的试验,却没有在相关文献中报道类似的结果。
2.3 天地相关性研究
飞行器气动力特性天地相关性研究,是飞行前预测数据和飞行数据比较的深化和提炼,其基本内容是:试图找到某个关联参数,建立起飞行的气动力特性与综合运用地面风洞、理论研究等各种手段得到的飞行器气动力特性关系。如果基于这个关联参数的天上飞行获得的气动力特性曲线同预测的飞行器气动力特性曲线重合(图 19[5]),就表明该参数对飞行器的气动力特性具有良好的天地相关能力。通过天地相关性分析,查找天地气动力差异的原因(图 15和图 16的关联曲线,揭示了舵面效率的预测是准确的,高超声速纵向配平异常与舵面效率无关,真实气体效应和马赫数效应导致的轨道器俯仰力矩误差是主要原因[14]),将为推动地面预测手段的发展、发现新的流动机理、建立气动力外推方法等方面提供指引。
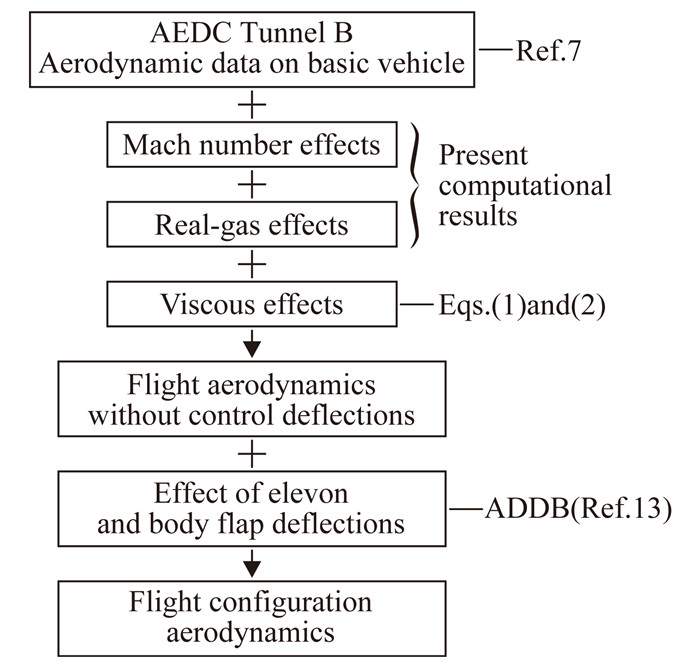
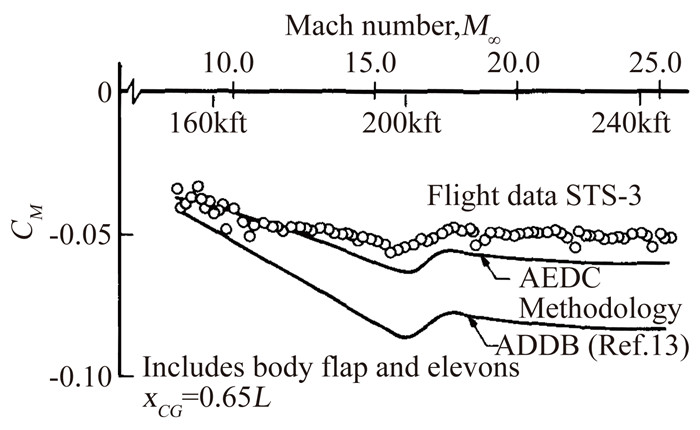
Maus等人[15]在吸收天地气动力差异研究成果的基础上,发展了高超声速气动力由地面数据外推到飞行条件的方法(图 20)。其中轨道器基本构形的马赫数效应、真实气体效应采用无粘流动数值模拟得到,黏性效应综合运用黏性流动计算和半理论分析得到,舵面效率直接采用飞行前预测数据。图 21为俯仰力矩曲线[15],图中“AEDC Methodology”为采用图 20所示外推方法得到的数据,与飞行前ADDB数据相比,同飞行数据的吻合度有了明显改善,如果采用该方法得到的数据来控制真实飞行,就不会出现“高超声速纵向配平异常”的问题。
上述气动力外推方法的实质就是:补上地面预测数据中没有包括的物理现象的影响。显然,对于地面风洞设备尚无法模拟的流动物理机制,有已经认知和掌握了的,但也有还没有认知和掌握的。对于物理机制认知的情况,在飞行试验前,可以通过理论分析(包括经验关联公式) 结果和数值模拟的手段来补偿地面预测数据中的物理效应的缺失,获得天上飞行环境下的气动力特性;对于缺乏物理认知的情况,飞行试验后,通过天地数据的差异,一方面,可以为探求新的流动现象提供指导,为空气动力学学科发展提供指引,另一方面,如果利用关联曲线能够寻找到差异规律,对于具体飞行器,直接把差异加到预测数据上,这是工程中气动力天地换算的另外一种途径。这种途径可以对几何类似的新飞行器气动力特性的不确定度提供指导[1],难以直接为地面预测得到气动力的外推提供帮助。
3 结束语航天飞机是人类载人航天的一个里程碑,回顾和审视历时30余年的气动特性研究过程,对目前临近空间飞行器的研制仍然有重要的警示和指导意义。我们对相关资料的阅读和思考,结合目前我国高超声速临近空间飞行器研制所了解的情况,得到以下一些初步认识:
1) 航天飞机高超声速纵向配平异常现象。为了掌握航天飞机轨道器的高超声速气动力特性的真实气体效应,在飞行前与飞行后,采用相同的数值方法(STEIN程序) 完成了计算分析和相同的风洞设备完成了不同比热比气体的试验测量。但飞行前发现的俯仰力矩的明显变化,应该是没有引起研究人员足够的重视,才出现了纵向配平异常现象。如果重视了,并进一步开展工作,分析这种差异会对配平舵偏角产生多大影响,避免出现所谓的“高超声速纵向配平异常现象”可能是大概率事件。
2) 多物理效应对舵面效率的影响。由航天飞机飞行试验数据分析得到的体襟翼舵面效率同飞行前预测结果一致,但数值模拟得到飞行条件下的舵面效率为飞行前预测结果的1.5倍[2]。文献中将这种差异归结为流动分离和比热比[14]。从纵向配平的角度看,数值模拟结果与飞行试验是一致的,但从舵面效率看,数值模拟结果同飞行试验又不一致。目前,作者尚未看到文献就此问题开展研究和讨论,并给出答案。到底是飞行试验原始数据的处理需要改进,还是数值模拟需要细化?高超声速飞行器真实气体效应的数值模拟,到目前为止,确实还存在诸多不确定元素[16-20],显然是一个讨论方向。
3) 气动力特性不确定度研究。航天飞机预测飞行前气动特性的不确定度的研究,所定义的不确定度只是马赫数的函数,同预设飞行弹道紧密相关,飞行姿态(迎角等) 的影响通过权重来体现。随着计算机和计算流体力学的迅猛发展,目前数值计算对气动力特性预测的贡献已上升到一个十分突出位置,对于无法采用单一风洞试验手段获得的包含复杂物理现象的飞行器流场及其气动力特性,综合运用风洞试验和数值模拟技术已成为获取飞行器气动特性的一种主流方式[20-22],但以此融合方式得到的气动力特性,如何合理地给出其不确定度,是目前需要克服的难题。事实上,如果航天飞机的不确定研究中,把俯仰力矩真实气体效应影响的计算结果以一种合适的方式考虑进去,所谓的“高超声速纵向配平异常现象”也不一定出现。
4) 风洞试验、理论分析(包含数值模拟技术) 和飞行试验数据的共享机制。众所周知,风洞试验、理论分析(包含数值模拟技术) 和气动飞行演示验证试验三大手段融合,是航天飞机气动研究给人们的重要启示之一,已成为持续推动高超声速飞行器创新设计和高超声速空气动力学学科发展的重要途径。目前,我国开展高超声速飞行器的气动演示验证飞行试验进入了前所未有的发展阶段,数值模拟技术已成为飞行器气动设计的重要支撑,急需建立数据共享机制,为三大手段融合扫除障碍,以谋求我国高超声速飞行器自主设计和高超声速空气动力学发展占有一席之地铺平道路。
下一步工作将基于我们对上述问题的认识,以航天飞机OV102外形为研究对象,围绕真实气体、黏性干扰等多物理效应对高超声速气动力特性的影响开展数值模拟研究。需要特别说明的是,本文所有数据结果及图片均来自所列参考文献。
| [1] | Young J C, Underwood J M. The development of aerodynamic uncertainties for the space shuttle orbit, Shuttle Performance:Lessons Learned, Part Ⅱ[R]. NASA CP-2283, Mar. 1983:1169-1180. |
| [2] | Woods W C, Arrington J P, Hamilton H H Ⅱ. A review of preflight estimates of real gas effects on space shuttle aerodynamic characteristics, Shuttle Performance:Lessons Learned, Part I[R]. NASA CP-2283, Mar. 1983:309-346. |
| [3] | Brauckmann G J, Paulson J W Jr, Weilmuenstar K J. Experimental and computational analysis of shuttle orbiter hypersonic trim anomaly[J]. Journal of spacecraft and Rockets, 1995, 32(5):758–764. DOI:10.2514/3.26680 |
| [4] | Brauckmann G J, Paulson J W Jr, Weilmuenstar K J. Experimental and computational analysis of shuttle orbiter hypersonic "pitch-up anomaly"[R]. AIAA paper 94-0632, 1994. |
| [5] | Romere P O, Whitnah A M. Space shuttle entry aerodynamic comparisons of flight 1-4 with preflight predictions, Shuttle Performance:Lessons Learned, Part I[R]. NASA CP-2283, 1983:283-307. |
| [6] | Young J C, Perez L F, Romere P O. Space shuttle entry aerodynamic comparisons of flight 1 with preflight predictions[R]. AIAA 81-2476, 1981. |
| [7] | Romere P O, Young J C. Space shuttle entry aerodynamic comparisons of flight 2 with preflight predictions[R]. AIAA 82-0565, 1982. |
| [8] | Kirsten P W, Richardson D F, Wilson C M. Predicted and flight test results of the performance, stability and control of the space shuttle from reentry to landing, Part I[R]. NASA CP-2283, 1983:509-515. |
| [9] | Compton H R, Schiess J R, Suit W T, et al. Stability and control over the supersonic and hypersonic speed range, Part I[R]. NASA CP-2283, 1983:473-508. |
| [10] | Calloway R L. Real gas simulation foe shuttle orbiter and planetary entry configurations including flight results[R]. AIAA 84-0489, 1984. |
| [11] | Szema K Y, Griffith B J, Maus J R. Laminar viscous flow-field predictions of shuttle-like vehicle aerodynamics[R]. AIAA 1983-0211. http://arc.aiaa.org/doi/pdfplus/10.2514/6.1983-211 |
| [12] | Maus J R, Griffith B J, Szema K Y, et al. Hypersonic Mach number and real gas effects on space shuttle orbiter aerodynamics[R]. AIAA 1983-0343. |
| [13] | Weilmuenstar K J, Gnoffo P A, Greene F A. Navier-Stokes simulations of orbiter aerodynamic characteristics including pitch trim and body flap[R]. AIAA 93-2814, 1993. |
| [14] | Griffith B J, Maus J R, Best J T. Explanaion of the hypersonic longitudinal stability problem-lessons learned, Shuttle Performance:Lessons Learned, Part I[R]. NASA CP-2283, 1983:347-380. |
| [15] | Maus J R, Griffith B J, Tolbert D G, et al. Understanding space shuttle flight data by use of wind tunnel and CFD results[R]. AIAA 83-2745, 1983. |
| [16] | Luckring J M, Hemsch M J, Morrison J H. Uncertainty in computational aerodynamics[R]. AIAA 2003-0409. https://www.researchgate.net/profile/James_Luckring/publication/23927856_Uncertainty_in_Computational_Aerodynamics/links/0f31753512da92fa57000000.pdf?origin=publication_detail |
| [17] | Weaver A B, Alexeenko A A, Greendyke R B, et al. Flowfield uncertainty analysis for hypersonic CFD simulations[R]. AIAA 2010-1180. |
| [18] | Stogner R, Bauman P T, Schulz K W, et al. Uncertainty and parameter sensitivity in multi-physics reentry flows[R]. AIAA 2011-764. |
| [19] | Hosder S, Benjamin R B. Uncertainty and sensitivity analysis for reentry flows with inherent and model-form uncertainties[J]. Journal of Spacecraft and Rockets, 2012, 49(2):193–206. DOI:10.2514/1.A32102 |
| [20] | Papadopoulos P E, Prabhu D, Wright M J, et al. CFD simulations in support of space shuttle orbiter contingency aerodynamic database enhancement[R]. AIAA 2001-3067. |
| [21] | Walter C, Scott D, Charles E. Aerodynamic database development for the Hyper-X airframe integrated scramjet propulsion experiments[R]. AIAA 2000-4006. https://hapb-www.larc.nasa.gov/Public/Projects/Hyperx.html |
| [22] | Prabhu D K, Papadopoulos P E, Davies C B, et al. Shuttle orbiter abort aerodynamics, Ⅱ:real-gas effects and high angles of attack[R]. AIAA 2003-1248. http://www.academia.edu/4484314/SHUTTLE_ORBITER_CONTINGENCY_ABORT_AERODYNAMICS_REAL-GAS_EFFECTS_AND_HIGH_ANGLES_OF_ATTACK |