风挡雨刷是广泛使用的除雨系统之一,主要作用是在降雨条件下,在飞机滑跑、起飞、进场、着陆阶段,为飞行员提供清晰的视界,保证飞行安全。风挡雨刷利用动力装置操纵雨刷刷片,在风挡玻璃外表面进行周期性往复运动,除去风挡玻璃上的雨水[1],如图 1所示。《运输类飞行适航标准》第773条(CCAR-25.773)规定:飞机必须具有措施使风挡玻璃在降水过程中保持有一个清晰的部分,足以使两名驾驶员在飞机各种正常姿态下沿飞行航迹均有充分宽阔的视界[2]。

|
| 图 1 风挡雨刷示意图 Fig. 1 Figure of the windshield wiper |
传统飞机风挡玻璃外形结构相对简单,大部分为平面玻璃,设计人员仅关注风挡表面刮刷清洁度、刮刷面积是否满足适航标准或国军标要求。随着科技的进步,运输类飞机逐步向长航时、高航速方向发展,为了保证整体气动外形,减小飞行中空气阻力,飞机上开始广泛使用复杂的多曲率风挡玻璃,导致风挡雨刷结构更复杂。由此,风挡雨刷在气动力作用下的功能是否正常得到了普遍关注。
目前,国外Zodiac等公司针对风挡雨刷的研究应用相对成熟,已研制出多款雨刷并投入批量生产,且分别使用数学方法、仿真软件和试飞验证对雨刷进行了气动力分析,但在相关文献及技术资料中仅见介绍风挡雨刷的功能及维修方法,未见对风挡雨刷气动力的相关内容报道[3]。国内风挡雨刷研究工作主要为了解决飞机型号设计和适航需求,与发达国家相比,研究存在一定的差距。对风挡雨刷的研究应用仅停留在产品的引进、消化、再吸收层面,并未深入开展雨刷气动力等关键技术参数的相关研究。试验研究领域由于缺乏雨风洞试验设施,只能进行简单的常规淋雨试验。
为了预防风挡雨刷在飞行过程中由于气动力的影响与风挡玻璃分离、飘起,本文对风挡雨刷的外形及复位位置进行了优化设计,并将优化前后风挡雨刷所受气动力进行了对比分析,为风挡雨刷预紧力设置和复位位置的确定提供依据。
通过求解N-S方程,结合S-A湍流模型,采用Fluent软件完成了风挡雨刷以不同角度停止于复位位置时,在不同飞行状态下的气动力计算,同时根据气动力计算结果,完成风挡雨刷复位位置的优化,并通过试飞对优化方案进行了验证。
1 计算过程 1.1 风挡雨刷模型选取某型机风挡雨刷作为优化对象,主要采取以下两种方案:1)改变雨刷停放角度;当风挡雨刷置于复位位置时,以风挡玻璃下边框为基准,分别将刷臂旋转2°、4°、6°;2)增加扰流板;风挡雨刷CATIA模型如图 2所示。

|
| 图 2 优化前后风挡雨刷模型图 Fig. 2 CATIA model of windshield wiper before and after optimized |
1.2 网格生成
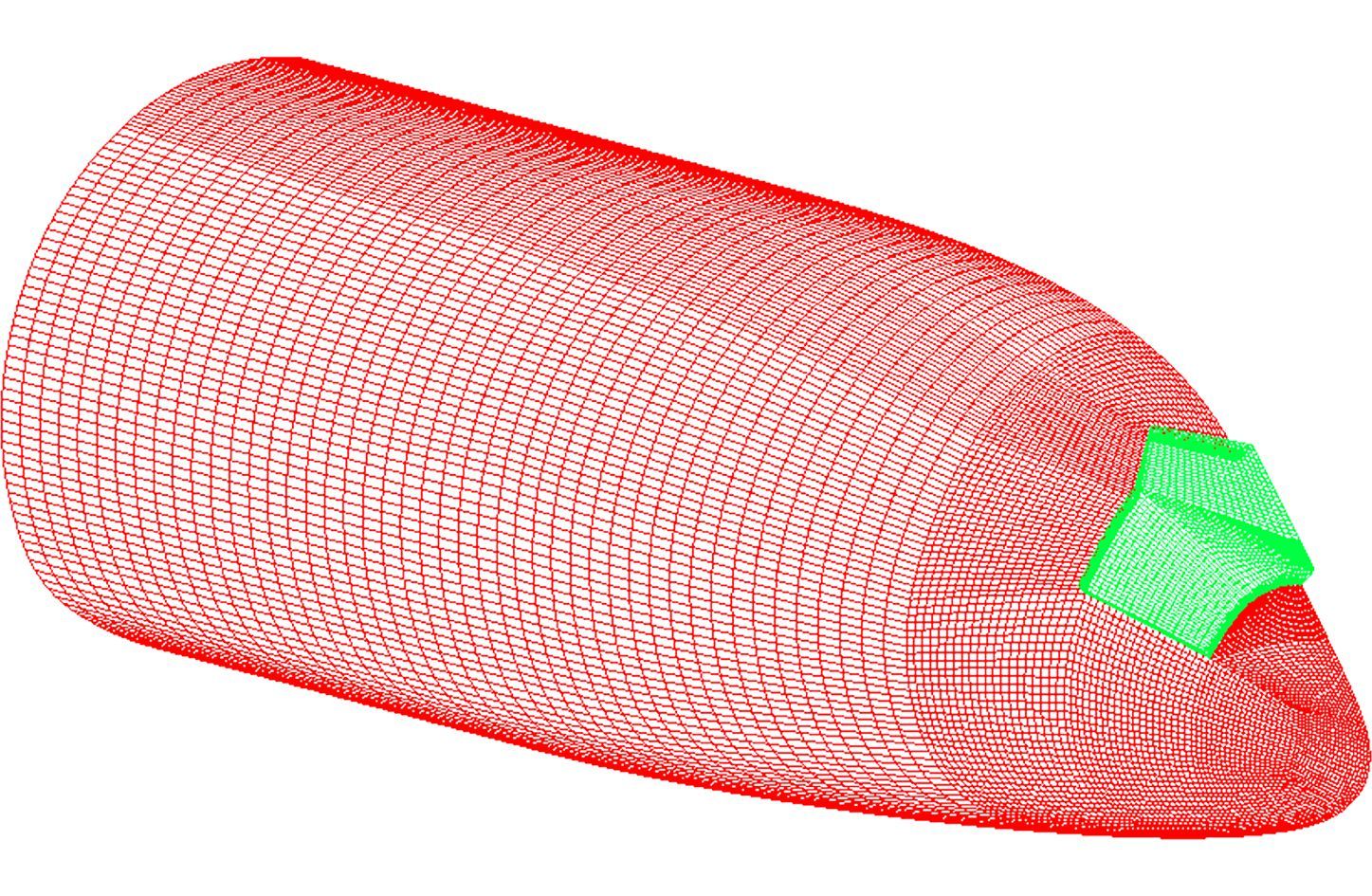
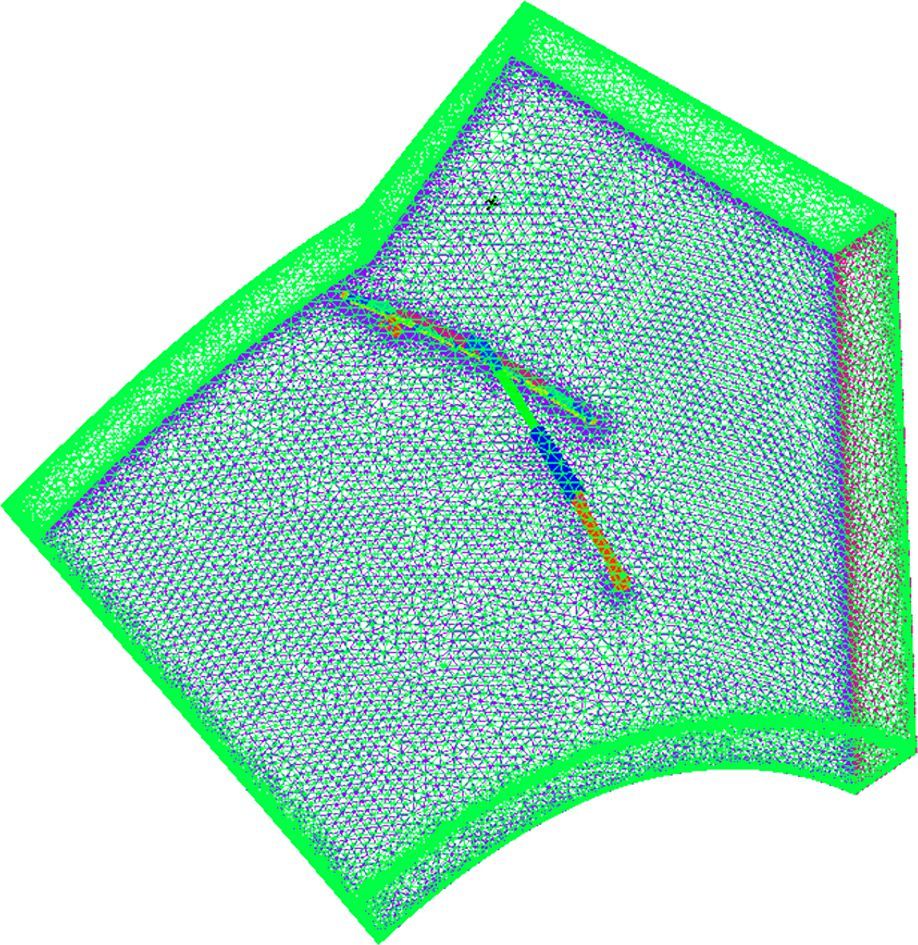
在风挡雨刷气动力计算中,由于机翼及尾翼等结构对风挡雨刷的流场影响很小,因而在计算过程中,忽略机翼、尾翼等结构,只选择整个机身作为计算区域,并对机身进行简化,减少计算量,提高计算效率。对计算区域采用结构化/非结构化的混合网格,在机身壁面附近生成结构化网格,而在远离固体表面的区域采用非结构化网格,同时在机头特别是风挡表面采用较细密的网格以保证计算精度。在生成网格时,仅保留机头和风挡雨刷系统的主要几何信息,忽略螺栓、保险丝及间隙等细节信息。整体网格见图 3,机身模型网格见图 4,风挡雨刷网格见图 5。

|
| 图 3 整体网格 Fig. 3 Overall mesh |
|
| 图 4 机身模型网格 Fig. 4 Fuselage model mesh |
|
| 图 5 风挡雨刷网格 Fig. 5 Windshield wiper mesh |
在网格划分中,由于机身的外形结构较规则,因此网格生成中将风挡玻璃及雨刷、机身部分分别生成网格,然后采用Interface面将两部分结合成最终计算网格,这样在改变风挡雨刷结构及风挡雨刷位置时仅需要重新生成风挡雨刷部分的网格,这种划分方式减少了由于网格不同而带来的计算误差。网格生成中,机身部分结构规则,采用结构网格;风挡雨刷部分存在多处镂空且结构复杂,采用非结构网格[6-7],并对局部进行加密。
1.3 控制方程风挡雨刷气动力计算使用Fluent软件、通过求解N-S方程,结合相应的湍流模型,采用时间平均法对不可压缩流的参数进行时均化[8]。N-S方程如下:
连续方程:
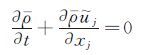
|
(1) |
动量方程:

|
(2) |
由于是可压缩流动,因此需要给定密度和热力学参数的关系。采用理想气体状态方程[9]:
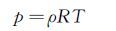
|
(3) |
式中,R为通用气体常数。
对于整机气动特性计算,由于网格数量巨大,因此采用S-A模型,湍流粘性系数如下所示:
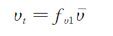
|
(4) |

|
(5) |

|
(6) |

|
(7) |
式中,υ为分子粘性系数,υ是计算湍流粘性系数的工作变量,S为旋度大小,d为距离物面的距离,且函数:
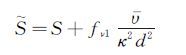
|
(8) |
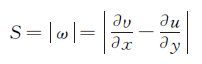
|
(9) |
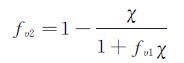
|
(10) |

|
(11) |
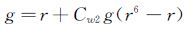
|
(12) |
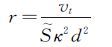
|
(13) |
式中,d为离最近的壁面的距离,各常数分别为: Cb1=0.1355;Cb2=0.622;Cυ1=7.1;σ=2/3;Cw2=0.3;Cw3=2.0;κ=0.41。
S-A模型建立时并没有考虑可压缩修正,但是只要在输运方程中考虑到密度的变化,S-A模型就可以用来计算可压缩流动[12]。
同时S-A模型可以直接积分到壁面,因此在计算中对靠近壁区域的网格进行加密,保证第一节点的y+为0.1~1[13]。
1.4 计算状态点| 序号 | h/m | α/(°) | v /(km·h-1) |
| 1 | 1000 | 0 | 450 |
| 2 | 1000 | 2 | 450 |
| 3 | 1000 | 4 | 450 |
| 4 | 1000 | 6 | 450 |
| 5 | 1000 | 0 | 550 |
| 6 | 1000 | 2 | 550 |
| 7 | 1000 | 4 | 550 |
| 8 | 1000 | 6 | 550 |
| 9 | 3000 | 0 | 450 |
| 10 | 3000 | 2 | 450 |
| 11 | 3000 | 4 | 450 |
| 12 | 3000 | 6 | 450 |
| 13 | 3000 | 0 | 550 |
| 14 | 3000 | 2 | 550 |
| 15 | 3000 | 4 | 550 |
| 16 | 3000 | 6 | 550 |
| 17 | 4000 | 1.5 | 650 |
| 18 | 5000 | 1.5 | 650 |
| 19 | 6000 | 1.5 | 650 |
| 20 | 7000 | 1.5 | 650 |
2 计算结果
将ICEM-CFD生成的计算网格导入Fluent软件,根据给定的计算条件进行相应的边界条件定义,采用二阶精度计算格式,对机身外流场进行计算,就可以获得风挡雨刷的气动力。由Fluent积分计算获得三维坐标方向的气动力矩,将所得坐标方向的力矩在风挡玻璃表面法线方向进行投影[15],可求得风挡雨刷在玻璃表面法向力矩,给出转轴中心至刷臂端点的距离,就可以算出刷臂端点的法向力。文中最终给出的是刷臂端点的法向力。
图 6~图 7是优化前后风挡雨刷在不同飞行条件下,典型状态风挡雨刷表面压力分布云图。

|
| 图 6 雨刷以不同角度停放时所受气动力 Fig. 6 Aerodynamic forces of the windshield wiper at the parking position with different angles |
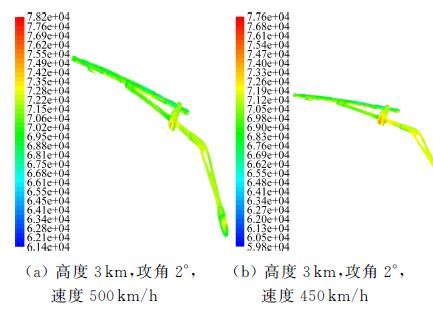
|
| 图 7 增加扰流板后雨刷所受气动力 Fig. 7 Aerodynamic forces of the windshield wiper at the parking position with different shapes |
表 2~表 4列出了雨刷在不同飞行高度、机身攻角及飞行速度所受的气动 力数值。其中F1表示优化前风挡雨刷在复位位置的迎风面法向力,F2表示优化雨刷停放角度并增加扰流板后,风挡雨刷迎风面法向力。
| 序号 | h/m | α/(°) | v /(km·h-1) | F1/N | F2/N |
| 1 | 1 | 1.5 | 650 | 36.5 | 34.6 |
| 2 | 3 | 1.5 | 650 | 35.2 | 32.8 |
| 3 | 4 | 1.5 | 650 | 33.1 | 30.6 |
| 4 | 5 | 1.5 | 650 | 31.1 | 28.7 |
| 5 | 6 | 1.5 | 650 | 29.0 | 25.3 |
| 6 | 7 | 1.5 | 650 | 26.7 | 23.6 |
| 7 | 8 | 1.5 | 650 | 23.9 | 21.5 |
| 序号 | h/m | α/(°) | v /(km·h-1) | F1/N | F2/N |
| 1 | 1 | 0 | 450 | 31.5 | 27.6 |
| 2 | 1 | 2 | 450 | 37.2 | 34.5 |
| 3 | 1 | 4 | 450 | 42.8 | 39.4 |
| 4 | 1 | 6 | 450 | 47.5 | 44.8 |
| 5 | 3 | 0 | 450 | 17.1 | 13.2 |
| 6 | 3 | 2 | 450 | 18.9 | 15.8 |
| 7 | 3 | 4 | 450 | 22.6 | 18.3 |
| 8 | 3 | 6 | 450 | 25.7 | 22.0 |
| 序号 | h/m | α/(°) | v /(km·h-1) | F1/N | F2/N |
| 1 | 1 | 2 | 450 | 37.2 | 34.5 |
| 2 | 1 | 2 | 550 | 46.1 | 42.7 |
| 3 | 1 | 2 | 650 | 59.3 | 52.6 |
| 4 | 3 | 2 | 450 | 18.9 | 15.8 |
| 5 | 3 | 2 | 550 | 26.4 | 23.6 |
| 6 | 3 | 2 | 650 | 36.2 | 33.4 |
3 计算结果分析
表 2计算结果表明,在一定飞行条件下,随着高度的增加,大气密度及大气压强减小,风挡雨刷所受气动力随之减小。表 3表明,当飞行马赫数增大时,绕流气流速度相对增大,故雨刷所受气动力增大。表 4表明,当攻角增大时,雨刷相对气流的迎风面积增大,以雨刷输出轴为中心的刷臂组件力矩增大,所以其气动力增大。
通过气动力对比分析,表明在所选的飞行状态下,优化前风挡雨刷在复位位置所受气动力约为17~59N。改变雨刷停止位置角度及增加扰流板后,气动力显著减小,其值为13~54N,雨刷迎风面所受气动力减少3.1~6.3N。
计算结果表明,雨刷以合理角度停放于复位位置能有效减小其迎风面所受气动力。此外,在雨刷刷臂加装精心设计的扰流板,能有效引导风挡雨刷迎风面气流的方向,从而减小雨刷迎风面所受气动力。
4 飞行验证将优化前后的风挡雨刷在某型机上进行试飞验证,验证状态点如表 5所示,优化前后的风挡雨刷装机件外形对比情况如图 8所示。

|
| 图 8 优化前后雨刷外形对比 Fig. 8 Comparison before and after the wiper optimization |
验证结果表明:在一定飞行条件下,优化前风挡雨刷由于气动力影响会轻微飘起,或周期性敲击蒙皮表面;对风挡雨刷停放位角度及外形优化后,此现象消失,雨刷各项功能正常。
5 结 论通过建立风挡雨刷仿真模型,利用Fluent软件,对不同飞行状态下风挡雨刷在复位位置所受气动力进行计算,并对风挡雨刷的停放角度进行优化,比较分析了计算结果,并进行了试飞验证。得出以下结论:
(1) 在一定飞行条件下,风挡雨刷所受气动力随着飞行高度的增加而减小,随着飞行马赫数的增加而增大,随着飞机攻角的增大而增大。
(2) 风挡雨刷在复位位置以合理角度停放可有效降低气动力,并可通过增加扰流板等措施降低其气动力。
(3) 雨刷的设计需与飞机进行气动力匹配计算和优化。
| [1] | Wang Z J, Edward L C. Unsteady aerodynamic effects on the flight characteristics of an F-16XL configuration[R]. AIAA 2000-39, 2000. |
| [2] |
Qiu X G, Han F H. Aircraft de-icing system[M]. Complication and Examination Group of Aero Specialized Teaching Materials. Beijing, 1985: 236-258. (in Chinese) 裘燮纲, 韩凤华. 飞机防冰系统[M]. 航空专业教材编审组. 北京, 1985: 236-258. |
| [3] | Frink N, Bonhsua D, Vatsa V. A boundary conditions for simulation of flow over porous surfaces[R]. AIAA 2001-2412. |
| [4] | Stuart E, Karlin R. CFD validation of high-lift flows with significant wind tunnel effects[R]. AIAA 2000-4218. |
| [5] |
Xu H Y, Ye Z Y. Numerical method for predicting rotor aerodynamic noise based on unstructured-grid CFD technology[J]. Acta Aerodynamica Sinica, 2007, 25(3): 325-329.(in Chinese) 许和勇, 叶正寅, 王刚. 基于非结构运动对接网格的旋翼前流场数值模拟[J]. 空气动力学学报, 2007, 25(3): 325-329. |
| [6] | |
| [7] | Frink N T. Recent progress toward a three-dimensional unstructured Navier-Stokes flow solver[R]. AIAA 94-0061, 1994. |
| [8] |
Wang G, Ye Z Y. A new way of determining nodal quantities for upwind schemes on unstructured meshes[J].
Journal of Northwestern Poly technical University, 2003, 21(2):248–252.
(in Chinese) 王刚, 叶正寅. 非结构网格迎风格式中的一种重构方法研究[J]. 西北工业大学学报, 2003, 21(2) : 248–252. |
| [9] |
Li D, Sun G, Qiao Z D. Use of chemera grid-embedding technique in complex configuration flow field calculation[J].
Acta Aerodynamica Sinica, 1998, 16(2):216–220.
(in Chinese) 李栋, 孙刚, 乔志德. 网格嵌套法在复杂流场计算中的应用[J]. 空气动力学学报, 1998, 16(2) : 216–220. |
| [10] |
Yang A M, Weng P F. Hyperbolic grid generation using upwind scheme[J].
Acta Aerodynamica Sinica, 2004, 22(1):109–113.
(in Chinese) 杨爱明, 翁培奋. 基于迎风格式的双曲型网格生成方法[J]. 空气动力学学报, 2004, 22(1) : 109–113. |
| [11] |
Liu F F, Yang C J, Su Q, et al. Simulation analysis and experimental research on the movements of biomimetic fin[J].
Journal of Mechanical Engineering, 2010, 46(19):24–29.
(in Chinese) 刘芳芳, 杨灿军, 苏琦, 等. 仿生鱼鳍运动仿真分析及试验研究[J]. 机械工程学报, 2010, 46(19) : 24–29. DOI:10.3901/JME.2010.19.024 |
| [12] |
Liu Q K, Qiao F G, Du Y L. Initial research of precipitation effect on aerodynamic characteristics of basic bluff[J].
Journal of Shijiazhuang Railway Institute(National Science), 2007, 20(4):14–20.
(in Chinese) 刘庆宽, 乔富贵, 杜阎良. 降雨对基本构件气动特性影响的初步研究[J]. 石家庄铁道学院学报(自然科学版), 2007, 20(4) : 14–20. |
| [13] |
Zhu B, Zhu X P, Zhou Z, et al. Simulation of unsteady multi-body flowfield involving relative movement based on unstructured mesh[J].
Acta Aerodynamica Sinica, 2013, 31(2):181–185.
(in Chinese) 朱冰, 祝小平, 周洲, 等. 基于非结构动网格的多体分离数值仿真研究[J]. 空气动力学学报, 2013, 31(2) : 181–185. |
| [14] |
Yang J T, Lou W J. Research on wind-driven rain CFD simulation and method calculating mean rain load[J].
Acta Aerodynamica Sinica, 2011, 29(5):601–606.
(in Chinese) 杨俊涛, 楼文娟. 风驱雨CFD模拟及平均雨荷载计算方法研究[J]. 空气动力学学报, 2011, 29(5) : 601–606. |
| [15] |
Zhang J H. Numerical simulation of the aerodynamic wiper on high-speed locomotives based on fluent[D]. Chengdu: Southwest Jiaotong University School of Mechanical Engineering, 2010. (in Chinese) 张军海. 基于Fluent的高速机车气动刮雨器数值模拟研究[D]. [硕士学位论文]. 成都: 西南交通大学, 2010. |


