现代战争对飞行器战术指标要求不断提高,固体火箭冲压发动机,以其独特的性能品质成为高速战术导弹推进系统的理想入选者。目前常用的进气道布局有中心进气和旁侧进气两种方式。由于二元进气道双下侧布局方式具有升阻比大、迎角性能好、横向空间占有小和便于机载等特点,在目前最先进的中程空空导弹研制(如欧洲的“流星”、美国的FMRAAM等)中被采用[1-2]。
导弹气动外形优化设计是导弹气动外形设计中的重要环节,直接影响飞行器的气动性能和飞行品质。气动外形优化方法很多,从本质上讲,把对设计对象的气动分析与优化设计方法相结合,通过对优化目标外形的不断调整,使优化对象的气动性能逐渐提高,直到满足给定的优化准则后,优化过程结束。此时的气动外形及气动性能便是在给定的约束条件下,采用该优化方法进行气动优化所能得到的最优解[3]。
国内外对于固体冲压导弹气动外形优化研究很多,但研究重点主要在高超声速飞行器、固体火箭冲压发动机自身以及发动机进气道性能的研究上。其中,文献[4-5]分别通过数值仿真和风洞试验设计并验证了结构简单、流量系数大、总压损失较小、压缩率高、性能稳定的典型二元双气道方案。文献[6-10]应用多目标遗传算法对高超声速导弹以及超燃冲压发动机进行一体化设计,更加系统而有效地获取了良好的几何和气动性能。遗传算法因为在理论上具有全局最优解、不需要计算灵活度、对设计空间无特殊要求等优点而被广泛采用在气动外形优化过程中。然而,由于算法全局最优解的收敛性很难满足,使其面临着严重的计算效率问题[11-12]。近年来,基于遗传算法的改进型方法很多。其中,Lee J等人提出了并行遗传算法的思想[13],Eric Besnard等人提出了遗传算法与模拟退火算法相结合的思想[14]。文献[15]针对气动外形优化设计中多设计点、多目标、多工程约束等特点提出了多设计快速优化的设计方法,通过简化优化设计模型,减少调用求解器的次数,提高优化效率。文献[16-17]提出了将遗传算法和局部搜索性能良好的优化算法相结合的办法。文献[18]解决了优化过程中的无显式约束问题,提出了收敛性更加高效的全模式遗传算法。
但是经过分析发现,文献中已开展的研究工作对于导弹定型设计阶段并不适用,并且优化效率不高。着眼于贴近工程实践,以某固冲导弹风洞试验模型为基准,着重对头罩、进气道、上下舵罩、舵面、弹翼等部件外形进行改进,建立了多个差异化模型,并采用CFD方法对各模型进行流场数值模拟,分析对比选型中各模型气动力结果,确定了优化后的最终外形。随后,对最终选型进行组拆选型试验、堵锥模型测力试验,将试验结果与相同状态下数值计算结果进行比较,为该固体冲压导弹进一步设计提供参考。
1 几何模型原导弹弹头形状为哈克型,进气道位于弹体双下侧与水平线成45°夹角位置。图 1给出了优化选型的基准外形(基准弹的风洞试验模型)。

|
| 图 1 基准外形 Fig. 1 Basic shape |
在 标准大气条件下,马赫数2.5、高度10km状态,一系列的风洞试验表明,基准外形的纵向静稳定性、0°攻角对称性、航程阻力和舵面舵效等性能均有待提高。针对这些问题,在全新进气道尺寸和质心要求的前提下,着重对基准弹头罩、进气道、弹翼、舵面、上下舵罩等部件参数进行修正,建立了以下4种选型模型。
相较于基准外形,模型A相应地增大了进气道的横截面积,减小了弹翼根梢弦尺寸,增大了上舵罩长度和宽度,以及下舵罩宽度和下舵罩收缩角,采用了内切角15°的大堵锥结构。图 2给出了该模型的几何外形。

|
| 图 2 模型A Fig. 2 Model A |
相较于模型A,模型B相应地增大了头锥长度,减小了舵面根弦和半展长尺寸,进一步减小了弹翼根梢弦尺寸,显著增大了上舵罩长度,将弹翼位置后移至上舵罩上,增大了下舵罩收缩角,并增加了舵面边条,采用了内切角5°、外切角3°的堵锥结构。图 3给出了该模型的几何外形。

|
| 图 3 模型B Fig. 3 Model B |
相较于模型B,模型C去掉了舵面边条,去除了弹翼,减小了上舵罩长度,在上下舵罩之间增加了一对水平尾翼,采用了双后掠角舵面。图 4给出了该模型的几何外形。

|
| 图 4 模型C Fig. 4 Model C |
相较于模型C,模型D恢复了舵面边条、弹翼,并将弹翼置于上舵罩之上,保留了水平尾翼和双后掠角舵面,进一步缩小了舵面尺寸。图 5给出了该模型的几何外形。

|
| 图 5 模型D Fig. 5 Model D |
2 CFD数值模拟 2.1 控制方程
采用FLUENT 6.3对导弹模型进行数值计算。就导弹的外流场而言,忽略空气重力,没有加质和能量源项,因此有强守恒型N-S方程[19]。
连续方程:
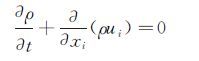
|
(1) |
动量方程:

|
(2) |
能量方程:

|
(3) |
式中,ρ为密度,p为静压,T是静温,kλ为导热系数,ui为速度矢量的分量,τij是粘性应力张量。
数值计算中,采用有限体积法对控制方程进行离散。选用耦合隐式求解器,理想气体模型。空间离散格式为二阶迎风格式,近壁区采用壁面函数法求解,湍流模型取可实现的k-ε模型。
2.2 计算域构造及网格划分采用结构化网格离散弹体表面及计算域。由于所涉及的计算状态不考虑弹体侧滑的影响,为了减少计算时间、提高计算效率,在纵向对称面处应用了对称边界条件,仅取其半模进行流场计算[20]。计算域的建立采用以弹体轴线为中心线的半圆柱形区域,其直径为弹体直径的10倍,长度为弹长的3倍。图 6给出了流场计算域构造。

|
| 图 6 计算域构造 Fig. 6 Computed field |
在构造的流场域进行网格划分,导弹外流场划分为六面体结构化网格。考虑激波对气流的作用,在弹头、弹翼、舵面、舵罩等区域对网格进行加密。半模模型网格总数约为6×105左右。图 7给出了壁面和外流场网格划分。

|
| 图 7 流场计算网格 Fig. 7 Computing grid of flow field |
2.3 结果分析与对比
进气道工作马赫数为2.0~3.5,根据需求,选取了设计点飞行马赫数为2.5,攻角0°和4°进行计算。
图 8给出了各模型的表面压力云图。表 1列出了各模型0°和4°攻角条件下的轴向力系数CA、法向力系数CN、对弹体顶点的俯仰力矩系数Cm0和相对焦点位置的俯仰力矩系数CmF计算结果。

|
| 图 8 各模型的表面压力云图 Fig. 8 Surface pressure contour of each model |
| α=0° | α=4° | CmF | |||||
| CA | CN | Cm0 | CA | CN | Cm0 | ||
| 基准弹 | 1.3869 | -0.4490 | -0.4480 | 1.4013 | 1.4935 | 0.9625 | 0.4553 |
| 模型A | 1.4458 | -0.5615 | -0.5431 | 1.4524 | 1.4636 | 0.7940 | 0.4578 |
| 模型B | 1.3652 | -0.3102 | -0.3107 | 1.3719 | 1.6591 | 1.1565 | 0.4803 |
| 模型C | 1.3220 | -0.3284 | -0.3204 | 1.3227 | 1.2248 | 0.7883 | 0.4146 |
| 模型D | 1.3403 | -0.3660 | -0.3503 | 1.3529 | 1.5812 | 1.0915 | 0.4733 |
由表 1可知:
1) 模型A的阻力系数大于基准弹,这主要源于进气道尺寸的增加;零位不对称性的增强,主要源于进气道和下舵罩负法向力的增加;15°的堵锥内切角使堵锥与弹体干扰增强,并在弹体表面和进气道间形成了局部高压区(图 8b)。
2) 模型B的阻力系数显著减小,这主要源于长头锥和堵锥内切角的减小;5°的堵锥内切角使堵锥和弹体间的干扰明显减弱(见图 8c);下舵罩前部收缩角增加改善了零位不对称性;舵面边条、弹翼位置后移使得焦点位置后移,静稳定性有所增加。
3) 模型C的阻力系数进一步减小,这主要源于减小上舵罩长度和去除舵面边条;去除弹翼和舵面边条使焦点位置大大前移,舵面法向力减小。
4) 模型D的阻力系数小于基准弹;舵面面积减小致使上下舵面舵效降低;水平尾翼弥补了舵面面积减小带来的焦点前移。
综上所述,模型A阻力系数大于基准弹;模型C焦点前移,使其静稳定度降低;模型B相对于模型D的双后掠角舵面而言,舵效偏高。出于减小阻力、增加静稳定性、降低舵面效率的考虑,确定模型D为最佳选型,进行下一步风洞试验。
3 风洞试验 3.1 组拆选型试验风洞试验过程中将各部件逐步组装到光弹体上,从而形成了16种不同的模型状态,并通过风洞试验最终得到了各模型的气动特性数据。图 9给出了组拆模型的外形及其部件名称。

|
| 图 9 组拆部件模型 Fig. 9 Components combination and diversion of the model |
各主要模型相对于模型D的试验结果对比情况如下:
1) 在不加堵锥的情况下,模型阻力将增加20%~30%,平衡攻角将增加4°;
2) 在没有舵面边条的情况下,模型的法向力系数将减小12%,纵向焦点位置将前移3.5%;
3) 在没有水平尾翼的条件下,模型的法向力系数将减小1.4%,纵向焦点位置将前移1%;
4) 弹翼对模型法向力的贡献为11%~14%,大小弹翼对应的法向力差异为3%,对纵向焦点的贡献差异为0.3%;
5) 大小舵面对应的法向力差异为2%,对纵向焦点的贡献差异为0.3%。
经过对比分析,最终选定了“光弹体+进气道+电缆罩+堵锥+上下舵罩+上下舵边条+大弹翼+小舵面+水平尾翼”模型组合作为优化后导弹的最终外形。图 10给出了试验模型在风洞中的照片。

|
| 图 10 试验模型在风洞中的照片 Fig. 10 Model in wind tunnel |
3.2 堵锥状态测力试验
堵锥状态测力试验共进行了64个车次的风洞试验,试验马赫数范围2.0~3.5,攻角范围-5°~10°、侧滑角-2°~2°。将优化弹的各项性能与基准弹的数据进行了对比。
3.2.1 纵向静稳定性图 11给出了Ma=2.5和Ma=3两种条件下纵向焦点位置随攻角变化曲线。如图所示,两种马赫数条件下,优化弹的纵向焦点位置平均后移3%左右。考虑到质心的差别(配重减轻15kg,质心后移3%)后,两者堵锥状态的静稳定度相当。并且,计算得到的焦点位置与试验值吻合良好,二者最大误差在1%左右。

|
| 图 11 纵向焦点位置随攻角变化曲线 Fig. 11 Longitudinal focus position vs. attack angle |
3.2.2 轴向力系数
图 12给出了Ma=2.5和Ma=3两种条件下轴向力系数-攻角曲线。如图所示,两种马赫数条件下,优化弹的轴向力系数数值减小了3%~4%,达到了优化减阻的设计目的。并且,计算得到的轴向力系数与试验值吻合良好,二者最大误差在1.5%左右。

|
| 图 12 轴向力系数随攻角变化曲线 Fig. 12 Axial force coefficient vs. attack angle |
3.2.3 气动不对称性
图 13给出了Ma=2.5、Ma=3.0两种条件下相对质心的俯仰力矩系数随攻角变化曲线。如图所示,优化弹的平衡攻角较基准弹减小1.5°(60%)左右。同时计算得到的俯仰力矩系数与试验得到数值吻合较好,二者最大误差在20%左右。

|
| 图 13 俯仰力矩系数随攻角变化曲线 Fig. 13 Pitching moment coefficient vs. attack angle |
表 2给出了在Ma=2.5、Ma=3.0两种条件下,试验得到的0°攻角对 称性数据。由表 2可知,优化弹的 轴向力系数、法向力系数和俯仰力矩系数均有所减小。
| Ma=2.5 | Ma=3.0 | |||||
| CA | CN | Cm0 | CA | CN | Cm0 | |
| 基准弹 | 1.35475 | -0.35291 | 0.07092 | 1.27138 | -0.33774 | 0.07577 |
| 优化弹 | 1.34161 | -0.30826 | 0.03285 | 1.25545 | -0.27672 | 0.04744 |
3.2.4 横测稳定性
图 14给出了优化前后导弹的斜吹力矩系数-随攻角变化曲线。由图,小攻角范围内,两弹斜吹力矩系数斜率差别不大;大攻角情况下,Ma=2.5,优化弹斜吹力矩系数斜率绝对值大于基准弹,但其对攻角的偏导数仍为负值,具备横侧自稳定性;Ma=3.0,两种外形的斜吹力矩系数斜率相当,均具有横侧稳定性。同时计算得到的斜吹力矩系数与试验得到吻合较好,二者最大误差在25%左右。

|
| 图 14 斜吹力矩系数斜率随攻角变化曲线 Fig. 14 Oblique moment coefficient vs. attack angle |
3.2.5 舵面效率分析
图 15和图 16给出了Ma=2.5条件下得到的俯仰和滚转舵效随攻角变化曲线。由图可见,优化弹对质心的俯仰舵效较基准弹减小了40%左右,滚转舵效减小了35%左右。并且,计算得到的俯仰和滚转舵效与试验数据吻合较好,二者最大误差在10%左右。另外,根据气动设计准则,优化弹的俯仰、偏航、滚转通道的独立性和操纵裕度均满足要求。

|
| 图 15 俯仰舵效随攻角变化曲线(Ma=2.5) Fig. 15 Pitching rudder effect vs. attack angle(Ma=2.5) |

|
| 图 16 滚转舵效随攻角变化曲线(Ma=2.5) Fig. 16 Rolling rudder effect vs. attack angle(Ma=2.5) |
4 结 论
优化弹的模型风洞试验,结果基本满足风洞试验精度要求,并与同条件下的计算结果吻合较好。
根据与基准弹风洞试验结果的对比可知,优化弹采取的气动优化措施得当,达到了预期的效果,可以为下一步该导弹型号研制提供参考。具体结果如下:
1) 优化后导弹的纵向焦点位置平均后移3%左右,考虑到质心位置后移3%的情况,静稳定度与基准弹相当;
2) 阻力有所减小,堵锥状态下的轴向力相比基准弹减小3%;
3) 平衡攻角相较于基准弹有所减小,零位法向力和零位俯仰力矩系数均有所减小,零位对称性明显增强;
4) 斜吹力矩系数和基准弹相当,横侧静稳定性满足飞行要求;
5) 滚转舵效较基准弹减小35%左右,俯仰舵效减小40%左右,达到了降低舵效的目的。
| [1] | Hayes C. Aerodynamic characteristics of a series of twin-inlet air-breathing missile configuration. Ⅱ: two-dimensional inlets at supersonic speeds[R]. NASA TM-84559, 1983. |
| [2] |
Xie L R, Guo R W. Experimental investigation of Fixed-geometry two-dimensional mixed-compression supersonic inlet with twin-inlet 90°configuration at venter[J].
Acta Aeronautica et Astronautica Sinica, 2009, 30(6):1000–1006.
(in Chinese) 谢旅荣, 郭荣伟. 双下侧定几何二元混压式超声速进气道的风洞试验[J]. 航空学报, 2009, 30(6) : 1000–1006. |
| [3] | Dulikravich G S. Aerodynamics shape design and optimization[R]. AIAA 91-0476, 1991. |
| [4] |
Li M, Song W Y, He W. Design method two-dimensional hypersonic forebody/inlet of mixed compression[J].
Journal of Propulsion Technology, 2004, 19(4):459–465.
(in Chinese) 黎明, 宋文艳, 贺伟. 高超声速二维混压式前体/进气道设计方法研究[J]. 航空动力学报, 2004, 19(4) : 459–465. |
| [5] |
Zhang X J, Liang D W, Li W, et al. Study of design method of typical two-dimensional hypersonic inlet[J].
Journal of Aerospace Power, 2007, 22(8):1290–1296.
(in Chinese) 张晓嘉, 梁德旺, 李博, 等. 典型二元高超声速进气道设计方法研究[J]. 航空动力学报, 2007, 22(8) : 1290–1296. |
| [6] | Hagenmaier M A, Davis D L. Scramjet component optimization using CFD and design of experiments[R]. AIAA 2002-0544. |
| [7] |
Liu J M, Hou Z Q, Song G B, et al. Optimization design and aerodynamic characteristic analysis of waverider based hypersonic cruise missile configuration[J].
Acta Aerodynamica Sinica, 2011, 29(1):118–122.
(in Chinese) 刘济民, 侯志强, 宋贵宝, 等. 高超声速巡航导弹乘波构型优化设计与性能分析[J]. 空气动力学学报, 2011, 29(1) : 118–122. |
| [8] |
Liu J M, Hou Z Q, Song G B, et al. Conceptual design and optimization for forebody/inlet of hypersonic cruise missiles[J].
Acta Aerodynamica Sinica, 2013, 31(3):321–325.
(in Chinese) 刘济民, 侯志强, 宋贵宝, 等. 高超声速巡航导弹前体/进气道概念设计与优化[J]. 空气动力学学报, 2013, 31(3) : 321–325. |
| [9] |
Xu D J, Sun B, Xu X, et al. Integrated design and optimization method for scramjet[J].
Journal of Propulsion Technology, 2002, 23(5):360–362.
(in Chinese) 徐大军, 孙冰, 徐旭, 等. 超燃冲压发动机一体化设计与优化方法研究[J]. 推进技术, 2002, 23(5) : 360–362. |
| [10] |
Luo W C, Chen X Q, Luo S B, et al. Genetic algorithm applied to integral design optimization of missile propelled by solid rocket ramjet[J].
Journal of Solid Rocket Technology, 2002, 25(3):1–4.
(in Chinese) 罗文彩, 陈小前, 罗世彬, 等. 固体火箭冲压发动机导弹一体化遗传算法优化设计[J]. 固体火箭技术, 2002, 25(3) : 1–4. |
| [11] |
Chang Y X, Gao Z H. Applicability analysis of genetic algorithms using in aerodynamic optimization[J].
Acta Aerodynamica Sinica, 2009, 27(2):167–172.
(in Chinese) 常彦鑫, 高正红. 遗传算法在气动优化问题中的适应性分析[J]. 空气动力学学报, 2009, 27(2) : 167–172. |
| [12] | Yamamoto K, Inoue O. Applications of genetic algorithms to aerodynamic shape optimization[R]. AIAA 95-1650, 1995. |
| [13] | Cook A M, Crossley W. Parallel genetic algorithm approaches to smart actuator placement for aircraft flight control[R]. AIAA 2000-1582. 41st AIAA/ASME/AHS/ASC Structures, Structural Dynamics and Materials Conference and Exhibit. Atlanta, GA, U. S. A., 2000. |
| [14] | Besnard E, Cordierlallouet N, Kural O, et al. Design/optimization with advanced simulated annealing[R]. AIAA 99-0186, 1999. |
| [15] |
Wang D, Bai J Q, Zhu J, et al. Fast optimization design with multi-requirements based on the analysis of partial correlation[J].
Acta Aerodynamica Sinica, 2014, 32(2):146–153.
(in Chinese) 王丹, 白俊强, 朱军, 等. 基于偏相关性分析的多设计要求快速优化设计方法[J]. 空气动力学学报, 2014, 32(2) : 146–153. DOI:10.7638/kqdlxxb-2012.0078 |
| [16] |
Gong C L, Gu Z F, Zhao J S, et al. Design and optimization of multi-stage solid launch rocket based on integrated stage concept[J].
Journal of Solid Rocket Technology, 2009, 32(1):1–5.
(in Chinese) 龚春林, 顾振芳, 赵吉松, 等. 基于整体级概念的多级固体运载火箭设计与优化[J]. 固体火箭技术, 2009, 32(1) : 1–5. |
| [17] |
Gu L X, Gong C L. A faster and better optimization of integrated design of integral rocket-ramjet missile with GACOM[J].
Journal of Northwestern Polytechnical University, 2004, 22(3):317–320.
(in Chinese) 谷良贤, 龚春林. 基于遗传算法的组合优化方法在整体式冲压发动机导弹一体化设计中的应用[J]. 西北工业大学学报, 2004, 22(3) : 317–320. |
| [18] |
Zhao J M, Xia Z X, Guo J, et al. Integral design optimization for missiles/solid rocket ramjets based on all schema genetic algorithm[J].
Journal of Solid Rocket Technology, 2005, 28(1):1–4.
(in Chinese) 赵建民, 夏志勋, 郭建, 等. 基于全模式遗传算法的导弹/固体冲压发动机一体化设计[J]. 固体火箭技术, 2005, 28(1) : 1–4. |
| [19] |
Jiang N, Wang Y W, Ling W H, et al. Integration performance analysis of typical arrangement inlet/missile[J].
Journal of Propulsion Technology, 2011, 32(4):451–454.
(in Chinese) 蒋妮, 王永卫, 凌文辉, 等. 典型布局的进气道/导弹一体化性能分析[J]. 推进技术, 2011, 32(4) : 451–454. |
| [20] |
Li X P, Yang M. Numerical study of inlet configuration effects on aerodynamic performance for air-breathing missiles[J].
Science Technology and Enginering, 2010, 10(35):8747–8751.
(in Chinese) 李雪萍, 杨茂. 进气道对导弹气动性能影响的数值研究[J]. 科学技术与工程, 2010, 10(35) : 8747–8751. |


