尾喷管是两级PDE的重要部件[1],其作用是将凹面腔内环形向心射流碰撞产生激波会聚起爆的爆震波排出,同时控制爆震波排出后下一个循环开始之前爆震燃烧室(凹面腔)内的压力。所以,尾喷管性能不仅仅会影响两级脉冲爆震发动机的推力性能,也会影响到爆震燃烧室的燃烧性能。近年来,国内外一些学者对传统脉冲爆震发动机的尾喷管进行了大量研究,大多数研究者认为[2-4]收敛-扩张喷管既能保持较高的充填压力又能降低排气温度和压力,相对于其他形式的喷管能获得最高的综合性能;也有部分研究者[5-6]认为安装扩张喷管和钟形喷管的推力性能最佳。相对于传统脉冲爆震发动机,两级PDE由于其独特的点火方式和燃烧的组织形式[7-15],所以对尾喷管的要求也不一样。而目前关于两级PDE尾喷管的研究较少。前期曾昊等研究了不同收敛-扩张角喷管对传统脉冲爆震发动机性能的影响[16](其结果表明收敛角为5°或扩张角为5°的收敛-扩张型喷管性能最优)和不同形式扩张喷管对两级脉冲爆震发动机性能的影响[17],其结果表明钟形大扩张角型扩张喷管性能最优。何立明等研究了尾喷管对2-stage PDE性能的影响[18],其结果表明带有45°扩张角的扩张喷管性能最优。在此基础上,本文选择在凹面腔上加装收敛、扩张、收扩等不同结构形式的喷管继续对两级脉冲爆震发动机性能进行研究,揭示喷管结构形式对凹面腔内环形激波聚焦起爆爆震波的作用规律和影响原理。
1 物理模型和计算方法 1.1 数值模拟的物理模型由于凹面腔内环形向心射流聚心碰撞产生激波会聚起爆爆震波的过程是一个射流、激波、爆震波三者之间相互作用的复杂过程,所以软件、模型的恰当选取对较好地模拟实际过程有很大的帮助。本文选择使用综合性高、通用性好、被该研究方向人员所普遍采用的FLUENT软件进行数值模拟。对于求解器,选择分离式求解器;湍流模型选择Realizable k-ε模型,并采用非平衡壁面函数及PISO算法,选用二阶迎风格式的方程离散格式。
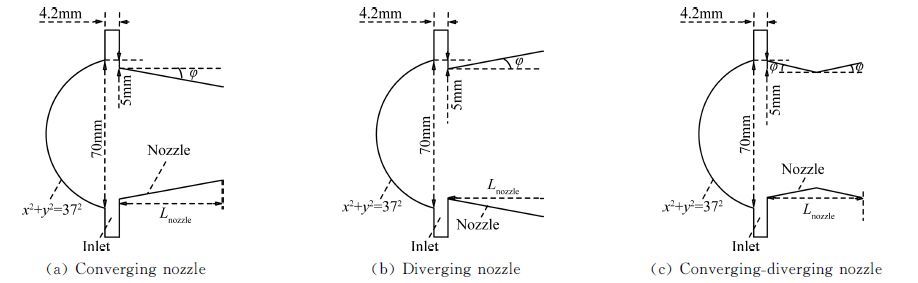
1.2 数值模拟的计算域凹面腔加装收敛、扩张、收扩三种结构形式喷管的示意图见图 1(为了显示方便,外流场区域未画出)。其中,凹面腔选择半径为37mm、开口弦长为70mm的部分球;环形向心射流喷口相对凹面腔的倾斜角为0°,喷口宽度为4.2mm;三种结构形式的喷管长度均取为LNozzle=50mm,其中收扩喷管的收敛段为25mm,扩张段为25mm。喷管进口直径均取为60mm,收敛角和扩张角均为φ=15°。
|
| 图 1 计算模型 Fig. 1 Schematic geometry configuration for the simulations |
因为凹 面腔-喷管结构具有轴对称性,为简化计算,数值模拟采用轴对称模型。其中,凹面腔及喷管为刚性、无滑移、绝热壁面 ,环形向心射流入口为压力入口边界;凹面腔及喷管内填充质量比为 0.02 ∶0.22 ∶0.76的H2/O2/N2混合气(即当量比为0.70的H2-空气混合气),初始压力p0=0.101MPa,温度T0=300K; 环形向心射流入口处混合气压力pin=0.45MPa,温度Tin=450K;凹面腔及喷管外区域为环境条件,填充空气,压力pa=0.101MPa,温度Ta=300K。激波会聚起爆的化学反应选用9组分31个基元反应的机理模型[19-20]。用爆震波的峰值压力和传播速度[21]来判断爆震是否成功转捩。爆震波的峰值压力可由压力等值线图读出,爆震波的传播速度可由不同时刻爆震波的前锋位置计算得出。
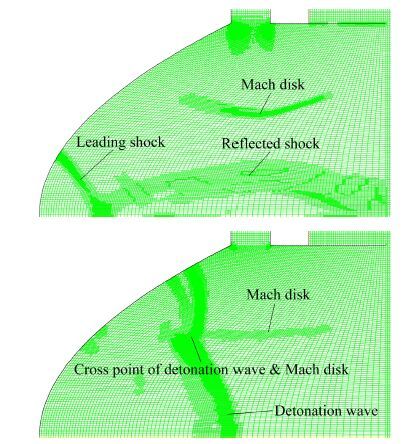
1.3 数值模拟的网格划分为有效捕捉到凹面腔内激波会聚起爆的爆震波,数值模拟的初始网格尺寸设为δ=0.1mm。由于研究的物理化学过程中存在射流、激波、爆震波三者之间相互作用的复杂流场结构,因此在数值模拟中使用了网格动态自适应加密方法(两层加密,最小网格0.01mm)。这种方法可用最少的计算资源有效地减小数值计算中的误差。从图 2所示的例子中可以清楚地看出,采用基于梯度的动态自适应加密方法[22]后,能够在激波或爆震波的压力和密度梯度发生剧烈变化的位置适时对网格进行加密,可用较少的计算资源有效地提高计算精度。
|
| 图 2 激波会聚起爆爆震过程中自适应动态加密网格举例 Fig. 2 Dynamic grids for detonation initiation |
1.4 数值模拟计算方法的验证
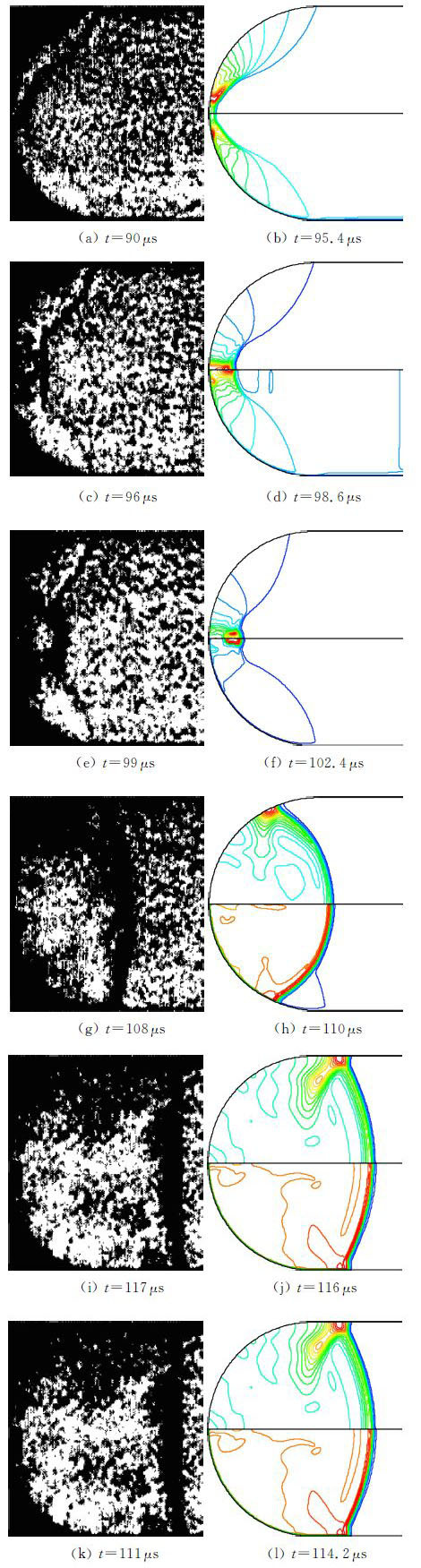
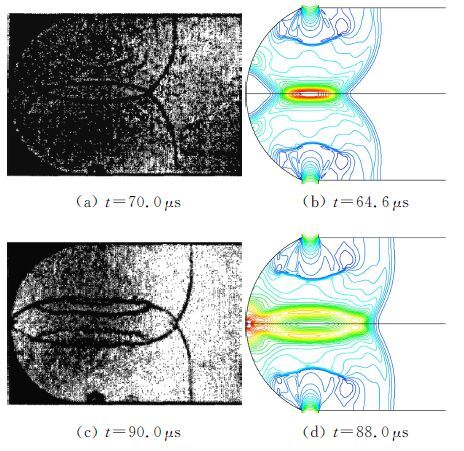
为了验证本文数值模拟激波会聚起爆的有效性,本节以H2/O2/N2混合气为介质对轴向入射的平面激波在凹面腔中反射会聚起爆及爆震燃烧的过程、以冷态空气为介质对环形向心射流在凹面腔中碰撞产生激波会聚的过程分别进行了模拟(公开发表的文献中,环形向心射流在凹面腔中碰撞产生激波会聚的模拟和实验获得的流场照片多是以冷态空气为介质),并与文献[23]中的实验影像结果进行了对比。对于轴向入射的平面激波,从图 3中可以看出,模拟结果与文献中实验照片所反映的激波经壁面反射、会聚起爆及爆震波以弧形向喷管开口端传播的整个过程吻合较好,模拟比较有效;对于环形向心射流(射流相对凹面腔倾斜角为0°),从图 4中可以看出,模拟结果与文献中实验照片所反映的射流入射到凹面腔内发生碰撞、产生激波会聚的整个过程吻合较好,模拟比较有效。
综上所述,经过对比分析,两个例子即轴向入射的平面激波在凹面腔中经过反射会聚起爆爆震波、环形向心射流在凹面腔中碰撞产生激波会聚起爆爆震波的模拟结果均与实验结果吻合较好,表明本文的数值模拟方法对激波会聚起爆爆震波过程的模拟是比较有效的,因此可以利用该方法对不同喷管结构形式的凹面腔内环形激波聚焦起爆爆震波过程进行模拟分析。
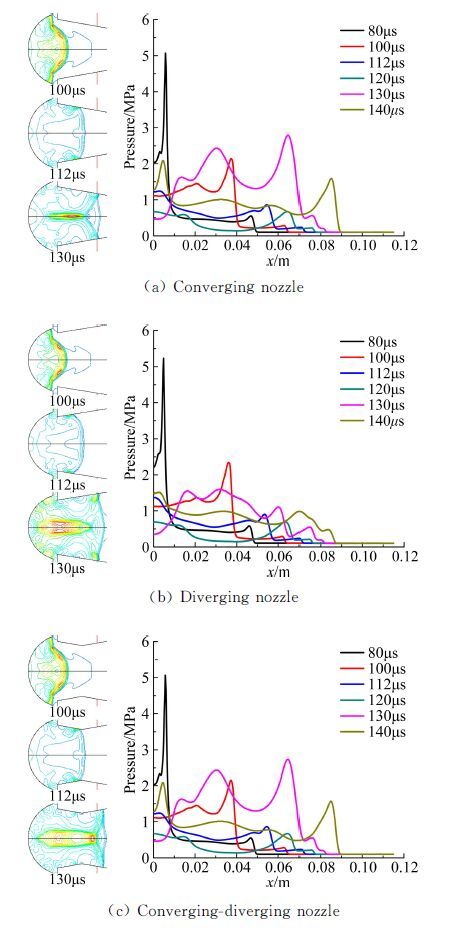
2 数值模拟结果与分析 2.1 数值模拟结果图 5为加装三种结构喷管的两级PDE的压力等值线图与中心轴线上的压力分布曲线。从压力等值线图可以看出,当t=100μs时,爆震波已经在凹面腔内形成并传播到喷管入口位置。而当t=112μs爆震波传入喷管时,由于喷管内填充的是空气,爆震波退化为一道无化学反应的激波。此后,由于喷管结构形式的不同,激波在喷管中的传播也会产生相应变化,并最终影响两级PDE的整体性能,具体分析如下。
|
| 图 5 加装三种结构喷管的两级PDE压力等值线图与压力曲线 Fig. 5 Pressure contours of 2-stage PDE with the three nozzles |
由图 5(a)可知,当激波传入收敛喷管时,由于传入的是收缩形的通道,激波在喷管内进行压缩并在喷管内壁产生反射,反射波回传入凹面腔对凹面腔壁面的压力产生影响。由凹面腔中心轴线上的压力曲线可以看出,爆震波是在t=100μs时传入喷管的,激波被压缩导致压力逐渐升高,在t=130μs时,喷管内压力最高点已经达到2.9MPa左右。随着反射激波的回传,凹面腔壁面的压力也由原先的0.45MPa逐渐上升;在t=140μs时,反射激波的压力峰值约为2.1MPa;之后撞击到凹面腔推力壁上的反射激波再次发生反射,使凹面腔内的压力再度上升。从以上的分析可以看出,加装收敛喷管后,由于激波在喷管收敛壁产生的反射激波的作用,凹面腔内的压力会有所上升,这对提高凹面腔的推力是有利的;同时,激波在喷管收敛壁上的反射产生了反向的喷管推力,这对提高喷管的推力是不利的。因此,收敛喷管自身对整个两级PDE性能的影响是不确定的,需要通过具体计算来确定。
由图 5(b)可以看出,当爆震波退化成激波传入扩张喷管时,由于扩张喷管所提供的扩张通道的膨胀作用,激波在喷管内进行扩张膨胀。从压力曲线上可以看出,从t=100μs激波传入喷管开始,激波的压力峰值是下降的,当t=130μs时喷管壁产生的反射波在中轴线汇聚后压力为1.6MPa左右,明显低于收敛喷管。回传入凹面腔的反射波峰值压力也较收敛喷管的低。从以上的分析可以看出,加装扩张喷管对凹面腔的推力没有很大影响,喷管内的压力也不是很高,但是由于扩张喷管提供的是正推力,所以两级PDE的整体性能会有所提升,具体提升情况需要计算求得。
由图 5(c)可见,爆震波退化成激波在收扩喷管中的传播情况与加装收敛喷管时的相似。对凹面腔来说,收扩喷管的收敛段依然产生了一个反射激波,它同样使得凹面腔内压力升高,在t=140μs时,凹面腔顶点压力达到1.25MPa,要低于加装收敛喷管时的压力峰值(1.3MPa)。由以上的分析可以看出,收扩喷管的收敛段可以使得凹面腔推力增加、喷管推力减少,而扩张段可以使得喷管推力增加,二者对两级PDE推力的影响相反,总的效果需要通过计算来确定。
2.2 定量分析由上面的分析可以得出,两级PDE所产生的推力和冲量会受到喷管结构形式(收敛、收扩、扩张)的影响。因此,可以认为两级PDE所产生的冲量是凹面腔产生的冲量和喷管产生的冲量的矢量和,即可由公式(1)对两级PDE所产生的总冲量进行计算。进而可以由式(2)、式(3)求得采用不同结构形式喷管的两级PDE的凹面腔产生冲量所占百分比和喷管产生冲量所占百分比,然后通过对Icavity、Inozzle、Itotal、αcavity、αnozzle变化规律的分析进一步揭示喷管结构形式对两级PDE性能的影响规律。
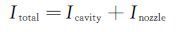
|
(1) |
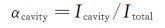
|
(2) |
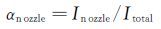
|
(3) |
图 6给出了加装三种结构形式喷管后的推力图和冲量图。在推力图中给出了一个爆震循环过程中凹面腔推力壁产生的推力、喷管壁面产生的推力和两级PDE的总推力。在冲量图中也给出了一个爆震循环过程中凹面腔产生的冲量、喷管壁面产生的冲量和两级PDE的总冲量。其中每一时刻的推力都是通过对壁面上的瞬时压力积分而得到的,冲量通过式(4)进行计算(式中A为凹面腔推力壁面积或喷管壁面投影面积)。
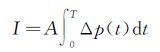
|
(4) |
|
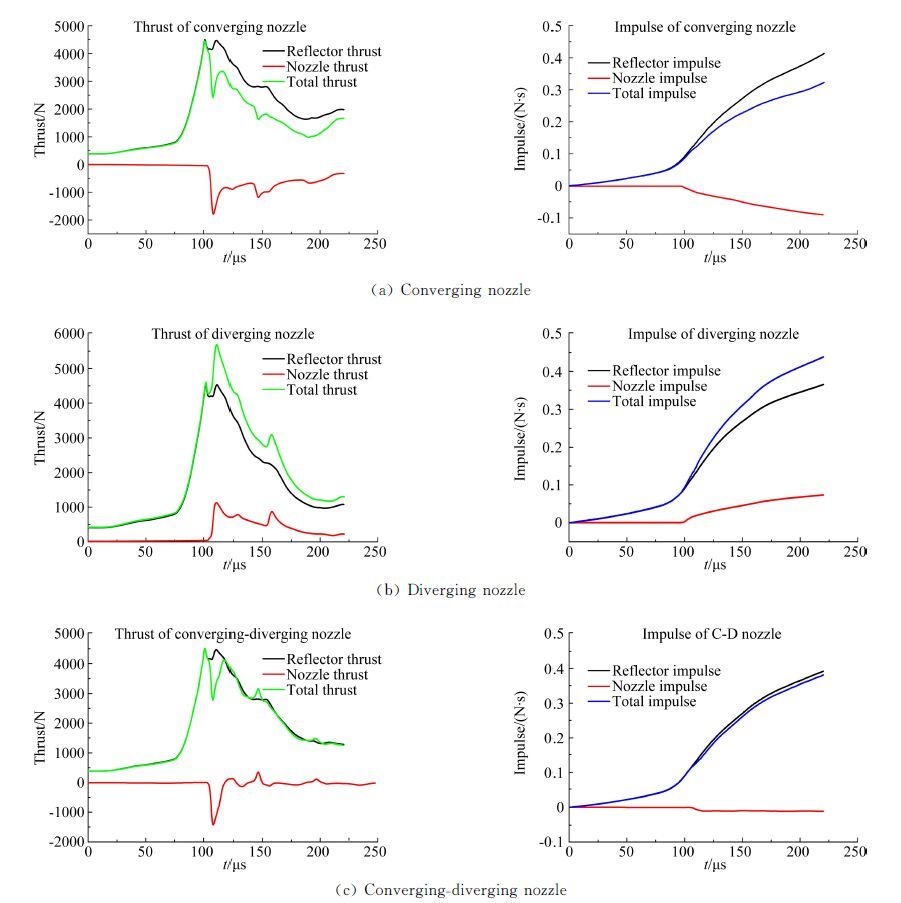
| 图 6 加装不同结构形式喷管的两级脉冲爆震发动机的性能曲线 Fig. 6 Performance curve of 2-stage PDE with the three nozzles |
如图 6(a)所示,安装收敛喷管时凹面腔的推力在t=101μs时逐渐增加到第一个峰值推力4468N,之后开始降低,在t=107μs时降低至4141N,而后又开始上升,在t=111μs达到第二个峰值推力4466N之后,凹面腔推力逐渐下降。当激波传入收敛喷管后,喷管开始产生负推力,而且由于收敛通道的压缩作用,喷管内的压力很高,所以喷管在t=108.5μs时产生了-1773N的负推力。根据推力曲线积分可得到冲量随时间的变化曲线,可以看出,在t=220μs时,凹面腔的冲量约为0.409N ·s,而喷管冲量约为-0.072N ·s,总的冲量为0.337N ·s。
由图 6(b)中可以看出,扩张喷管在激波传入后,由于其提供的是正推力,在t=110μs时喷管最大推力达到1125N,之后则由于压力下降过快,喷管的推力一直低于凹面腔的推力。从冲量图上可以看出,在t=220μs时,凹面腔提供了0.366N ·s的冲量,而喷管提供了0.073N ·s左右的正冲量,总的冲量达到了0.439N ·s。
由图 6(c)可以看出,安装收扩喷管时凹面腔的推力曲线与安装收敛喷管时凹面腔的推力曲线图 6(a)比较相似,凹面腔推力壁都有一个正向的推力峰值,该推力峰值出现在t=101μs,峰值为4497N,但其比加装收敛喷管时高了约29N。喷管的负推力峰值 -1430N出现在t=108.5μs左右,与安装收敛喷管时相比,负推力小了很多。从冲量曲线上可以看出,喷管的冲量虽然为负值,但是值不大,这是由于喷管的收敛段和扩张段的冲量要相互抵消一部分的缘故。在t=220μs时,凹面腔提供了0.392N ·s的冲量,喷管提供了-0.011N ·s 的冲量,总的冲量为0.381N ·s。
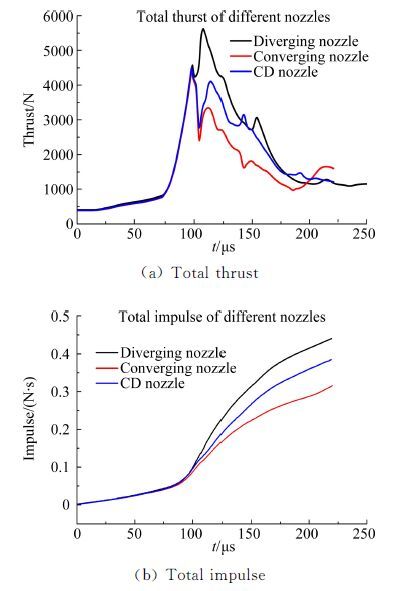
图 7是安装收敛、扩张、收扩三种不同结构形式 喷管时两级脉冲爆震发动机总推力、总冲量随时间变化曲线的对比图。由图 7(a)可以看出,在t=108.5μs时,一个向下的峰值推力产生于使用收 敛喷管、收扩喷管的情况,其大小分别为2428N、2819N,这是由于喷管的收敛段使传入的激波发生反射产生负推力造成的。而使用扩张喷管则在t=111.5μs时产生了三种喷管中最大的向上峰值推力5619N。从总的趋势看,使用收敛喷管、收扩喷管时两级脉冲爆震发动机获得的总推力低于使用扩张喷管时两级脉冲爆震发动机获得的总推力。由图 7(b)则可以看出,安装三种不同结构形式喷管的两级脉冲爆震发动机获得的总冲量由大到小依次是扩张喷管、收扩喷管、收敛喷管。
|
| 图 7 安装三种喷管时总推力、总冲量随时间变化曲线的对比图 Fig. 7 Comparison of total thrust and total impulse among the three nozzles |
表 1为t=220μs时安装收敛、扩张、收扩三种不同结构形式喷管时两级脉冲爆震发动机的凹面腔冲量、喷管冲量和总冲量的对比。通过表 1可以将喷管结构形式对凹面腔性能的影响进行比较。当使用收敛喷管时,凹面腔的冲量和冲量比均为最大,分别为0.409N ·s、121.36%;而使用扩张喷管时,凹面腔的冲量和冲量比均为最小,分别为0.366N ·s、83.37%;使用收扩喷管时,凹面腔的冲量和冲量比均为居中,分别为0.392N ·s、102.89%。由此可以看出,凹面腔的冲量比总是大于喷管的冲量比,即凹面腔产生的冲量对总冲量的贡献总是大于喷管产生的冲量的贡献。三种结构形式喷管提供的喷管冲量以收敛喷管为最低,收扩喷管次之,而只有扩张喷管的喷管冲量可以达到正值,且加装三种结构形式喷管时的总冲量也以扩张喷管为最高,由此可以看出,喷管的收敛结构会显著的提高凹面腔的冲量比,即喷管收敛段管壁产生的反射激波对凹面腔冲量的提高是十分有利的,但同时也使喷管的冲量比为负,使总冲量变小,即喷管收敛段管壁产生的反射激波对总冲量的提高是有害的。
| Nozzle configuration | Icavity/(N·s) | αcavity | Inozzle/(N·s) | αnozzle | Itotal/(N·s) |
| Converging nozzle | 0.409 | 121.36% | -0.072 | -21.36% | 0.337 |
| Diverging nozzle | 0.366 | 83.37% | 0.073 | 16.63% | 0.439 |
| C-D nozzle | 0.392 | 102.89% | -0.011 | -2.89% | 0.381 |
3 结 论
通过以上的数值模拟计算和结果分析,可以得到下面的结论:
(1) 不管两级PDE加装何种结构形式的喷管,凹面腔产生的冲量对总冲量的贡献总是大于喷管产生的冲量的贡献,说明凹面腔内激波会聚起爆的爆震波是两级PDE性能的主要影响因素。
(2) 不同喷管结构形式对两级PDE性能的影响有较大的差别。以冲量为例,收敛喷管可以提高凹面腔的冲量,但是由于自身同时产生过多负的喷管冲量,因而总冲量较小;扩张喷管虽然对凹面腔冲量的提高作用不大,但是由于其自身可以提供正的喷管冲量,所以总冲量较大;收扩喷管的收敛段也可以较小幅度的提高凹面腔冲量,但同时产生的负喷管冲量会和扩张段产生的正喷管冲量发生抵消,使总的喷管冲量比较低,发动机总冲量也较小。综合考虑各方面因素,扩张喷管性能最优。
(3) 对于两级PDE的喷管来说,收敛结构可以提高凹面腔冲量,但必须同时付出减少喷管冲量的代价;扩张结构对凹面腔冲量影响不大,但可以提高喷管冲量。因此要设计出一个合理的喷管,就必须在凹面腔冲量和喷管冲量之间找到平衡点,在努力提高凹面腔冲量的同时也尽量减少喷管负冲量的产生,从而使两级脉冲爆震发动机的性能最优。
| [1] | Eidelman B S. Pulse detonation engine: a status review and technology development road map[R]. AIAA 97-2740, 1997. |
| [2] | Barbour E A, Hanson R K. A pulsed detonation tube with a converging-diverging nozzle operating at different pressure ratios[R]. AIAA 2005-1307. |
| [3] | Barbour E A, Owens Z C, Morris C I. The impact of a converging-diverging nozzle on PDE performance and its associated flowfield[R]. AIAA 2004-867. |
| [4] | Daniel E Paxson. Optimal area profiles for ideal single nozzle air-breathing pulse detonation engines[R]. AIAA 2003-4512. |
| [5] | Zachary C O, Ronald K Hanson. Unsteady nozzle design for pulse detonation engines[R]. AIAA 2005-3649. |
| [6] | Yungster S. Analysis of nozzle effects on pulse detonation engine performance[R]. AIAA 2003-1316. |
| [7] | Ivett A Leyva, Venkat Tangirala. Investigation of unsteady flow field in a 2-Stage PDE resonator[R]. AIAA 2003-715. |
| [8] | Keith R M Manus, Anthony J. Dean experimental evaluation of a two-stage pulse detonation combustor[R]. AIAA 2005-3773. |
| [9] |
Wang D. Numerical investigation of the working process in PDE[D]. Nanjing: Nanjing University of Science and Technology, 2007. (in Chinese) 王栋. 脉冲爆震发动机工作过程数值模拟研究[D]. 南京: 南京理工大学, 2007. |
| [10] |
Jiang R H, Wu X S, Wang D. Matching research of resonant PDE's resonator and jet[J].
Journal of Aerospace Power, 2009, 24(5):1006–1010.
(in Chinese) 姜日红, 武晓松, 王栋. 共振型PDE谐振腔喷嘴匹配关系研究[J]. 航空动力学报, 2009, 24(5) : 1006–1010. |
| [11] |
Zhou H. Performance study of two-stage PDE[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. (in Chinese) 周鸿. 两步法高频爆震发动机机理与特性研究[D]. 南京: 南京航空航天大学, 2008. |
| [12] |
Li H P, He L M, Zeng H, et al. Numerical investigation of detonation initiation by shock wave focusing over paraboloid reflector[J].
Journal of Propulsion Technology, 2010, 31(1):87–91.
(in Chinese) 李海鹏, 何立明, 曾昊, 等. 凹面腔内激波聚焦起爆爆震波过程的数值模拟[J]. 推进技术, 2010, 31(1) : 87–91. |
| [13] |
Zeng H, He L M, Zhang X W, et al. Investigation on the influence of jet flow pressure on detonation initiation via imploding annular shock waves[J].
Journal of Aerospace Power, 2010, 25(9).
(in Chinese) 曾昊, 何立明, 章雄伟, 等. 入射压力对环形射流激波聚焦起爆爆震的影响分析[J]. 航空动力学报, 2010, 25(9). |
| [14] |
Zeng H. Experimental study and numerical simulation of two-stage pulse detonation engine[D]. Xi'an: Air Force Engineering University, 2011. (in Chinese). 曾昊. 两级脉冲爆震发动机的实验研究与数值模拟[D]. 西安: 空军工程大学, 2011. |
| [15] |
Zeng H, Chen X, He L M, et al. Investigation on two-dimensional shock wave focusing[J].
Aata Aerodynamica Sinica, 2013, 31(3):316–320.
(in Chinese) 曾昊, 陈鑫, 何立明, 等. 凹面腔内二维激波会聚特性研究[J]. 空气动力学学报, 2013, 31(3) : 316–320. |
| [16] |
Zeng H, He L M, Zhang X W, et al. Investigation on the effects of nozzles with different convergent-divergent angle on PDE performance[J].
Journal of Propulsion Technology, 2011, 32(1):97–102.
(in Chinese) 曾昊, 何立明, 章雄伟, 等. 喷管收敛-扩张角对爆震发动机性能影响分析[J]. 推进技术, 2011, 32(1) : 97–102. |
| [17] |
Zeng H, He L M, Wu C H, et al. Investigation for effects of diverging nozzles on two-stage PDE performance[J].
Journal of Propulsion Technology, 2013, 34(8):1139–1146.
(in Chinese) 曾昊, 何立明, 吴春华, 等. 不同形式扩张喷管对两级PDE性能的影响[J]. 推进技术, 2013, 34(8) : 1139–1146. |
| [18] |
Zhang Q, He L M, Li H P, et al. Investigation into the effect of nozzle on the 2-stage PDE performance through numerical simulation[J].
Journal of Air Force Engineering University (Natural Science Edition), 2011, 12(1):10–14.
(in Chinese) 张强, 何立明, 李海鹏, 等. 尾喷管对2-stage PDE性能影响的数值模拟[J]. 空军工程大学学报(自然科学版), 2011, 12(1) : 10–14. |
| [19] | Konnov A A. Refinement of the kinetic mechanism of mydrogen combustion[J]. Khimicheskaya Fizika, 2004, 23(8):5–18. |
| [20] | Konnov A A. Remaining uncertainties in the kinetic mechanism of hydrogen combustion[J]. Combust and Flame, 2008, 152(4):507–528. DOI:10.1016/j.combustflame.2007.10.024 |
| [21] |
Yan C J, Fan W.
The principle and key technology of pulse detonation engine[M]. Xi'an: Northwestern Polytechnical University Press, 2005 : 20 -22.
(in Chinese) 严传俊, 范玮. 脉冲爆震发动机原理及关键技术[M]. 西安: 西北工业大学出版社, 2005 : 20 -22. |
| [22] | Daunenhofer J F, Baron J R. Gird adaption for the 2D Euler equati ons[R]. AIAA 85-0484, 1985. |
| [23] | Achasov O V, Penyazkov O G. Some gasdynamic method for control of detonation initiation and propagation[C]//High Speed Deflagration and Detonation Fundamentals and Control. Moscow, 2001: 31-44. |