低速风洞单自由度大幅振荡试验技术是飞机研制,特别是具有过失速机动能力的战斗机研制所必需的试验技术。对相应的大幅振荡试验数据进行支架干扰修正,可大幅度提升数据的准度,为飞行器的气动特性准确预测和性能分析提供高质量、高可信度的数据。这对提高飞行器研制保障水平,对飞行器性能计算和安全性评估具有重要意义。
目前国内外均已经开发并应用了多自由大幅振荡试验系统,国外已有单位开展相应系统的支架干扰机理研究。加利福尼亚的Lars E Ericsson教授和专门从事非定常气动力研究的Reding教授对支架干扰进行了多年的研究,他们认为支杆的存在对飞机模型的尾迹有影响,它能引起涡的提前破裂,他们在风洞、水洞中,多方面、形象化地研究了支杆对涡破裂的影响,尤其是支杆的形状、安放位置的影响[1-6]。巴思大学的G S Taylor教授也通过试验研究了俯仰振荡中支杆不同位置对涡破裂的影响,指出动态试验的支架干扰问题更复杂[7-8]。国内虽然尚未对大幅振荡试验支架干扰进行相应研究,但已经开展过其他动态试验系统的支架干扰试验研究和大幅振荡试验洞壁干扰的试验研究[9-15]。中国航空工业空气动力研究院的高剑军和杜希奇分别对旋转天平和动导数试验系统的支架干扰进行了试验研究,其试验结果表明:在强迫振荡试验中,支架干扰对动态试验数据有明显的影响[8-9]。通过对试验数据进行支架干扰修正,可以进一步提高试验结果的准确性。虽然国外很早就开始了大幅振荡试验支架干扰影响研究,但仍然停留在机理研究,目前国内外大幅振荡试验支架干扰修正尚无面向工程应用的试验研究。
中国航空工业空气动力研究院“非定常气动力技术团队”在FL-51风洞对大幅振荡试验系统的支架干扰进行了探索性研究,通过两步法,获得了大幅振荡试验系统的支架干扰影响量,提高了大幅振荡试验试验结果的准度。
1 试验设备及模型 1.1 模型模型采用中国航空工业空气动力研究院动态试验标膜,为金属与复合材料混合结构,机身、机翼等主要部件采用高强度铝、高强度钢等金属材料作为主要承力和连接骨架,采用比强度、比刚度高的碳纤维壳体作为各种部件型面。模型主要参数见表 1,模型照片见图 1。

|
| 图 1 试验模型 Fig. 1 Test model |
1.2 风洞
FL-51风洞为开/闭口单回路低速风洞,试验段截面为矩形,风洞为开/闭口单回流式低速风洞,试验段尺寸4.5m(宽)×3.5m(高)×11m(长),闭口试验段最大风速100m/s,开口试验段最大风速85m/s。
1.3 双自由度大幅振荡机构试验系统采用电机/液压耦合驱动的双自由度运动,由液压伺服马达驱动弯刀运动,实现模型的俯仰(模型正装)运动或偏航(模型侧装)运动,电机驱动尾支杆实现模型的滚转运动。试验系统主要由上下连杆、液压马达、振荡弯刀、电机驱动装置、滚转支杆、液压管路和泵站等组成。除液压管路和泵站安装在风洞外侧,其余部件均安装在试验段中,见图 2、图 3。

|
| 图 2 大幅振荡试验系统结构图 Fig. 2 Structure of the large amplitude oscillation test system |

|
| 图 3 FL-51风洞大幅振荡试验照片 Fig. 3 Large amplitude oscillation test system in FL-51 |
机构运动指标见表 2。
| 运动模态 | 运动指标 |
| 滚转振荡(小轴) | 2Hz,45° |
| 偏航振荡(大轴) | 1Hz,45° |
| 俯仰振荡(大轴) | 1Hz,45° |
大幅振荡试验角度变化规律如下:
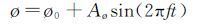
|
(1) |
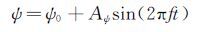
|
(2) |
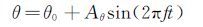
|
(3) |
其中θ为支杆俯仰角,ψ为偏航机构角,φ为支杆滚转角。
1.4 测控系统及数据处理系统天平测得的电信号由FL-51风洞VXI采集系统采集,数字信号由工控机处理,试验原始数据由大幅振荡试验处理程序处理成中苏坐标轴系下的体轴六分量系数。动态滤波采用傅里叶变换数字滤波器,试验现场可以实时显示曲线。
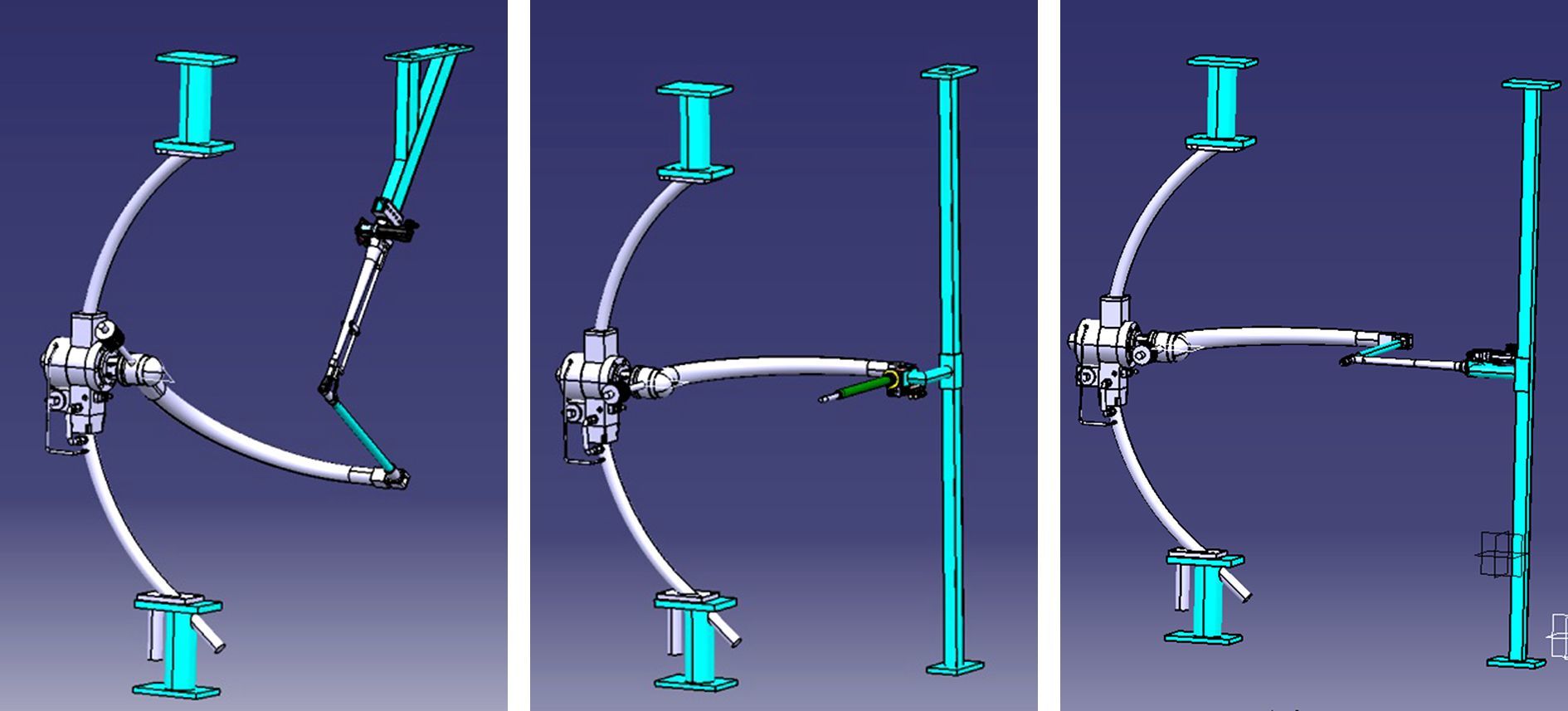
1.5 支架干扰辅助支撑系统支架干扰辅助支撑系统由俯仰、滚转和偏航辅助支撑系统组成,如图 4所示。辅助支撑系统的俯仰、滚转和偏航运动均由电机驱动。
|
| 图 4 俯仰、滚转及偏航辅助支撑系统结构图 Fig. 4 Structure of assist support system |
2 试验方法
模型采用内式天平,支架干扰只有支架对模型气动力的干扰项。采用两步法进行俯仰、滚转和偏航大幅振荡试验支架干扰的试验修正。两步法支架干扰修正方法使用叠加原理,认为辅助支架、映像支架和主支架对模型气动力的干扰作用都是线性叠加关系,没有考虑不同支架之间的相互干扰。除模型试验外,要进行两步带辅助支架的辅助试验,如图 5所示。

|
| 图 5 偏航振荡支架干扰两步法试验照片 Fig. 5 Pictures of the method to measure the support interference |
模型试验和辅助试验的气动力分别为:
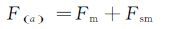
|
(4) |
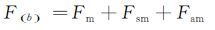
|
(5) |
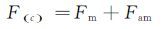
|
(6) |
式中,下标am表示辅助支架对模型的干扰,m表示模型,sm表示支架对模型的干扰。
扣除支架干扰后的模型气动力为:
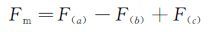
|
(7) |
上述的试验修正法都使用了叠加原理,即认为辅助支架、映像支架和主支架对模型气动力的干扰作用都是线性叠加关系,没有考虑不同支架之间的相互干扰。
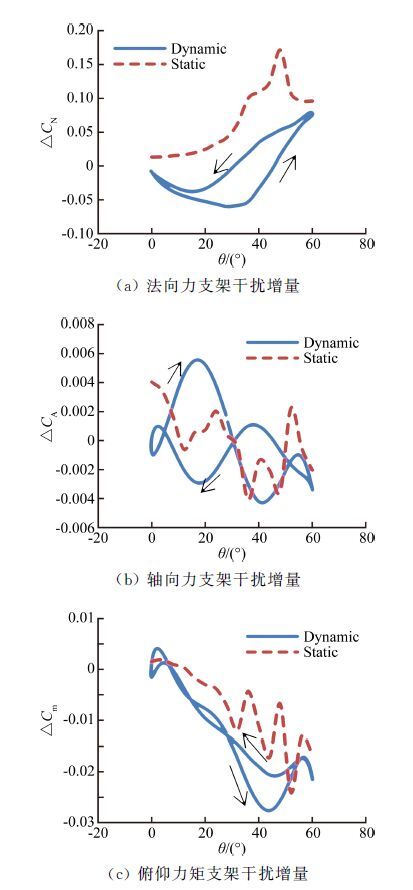
3 试验结果分析 3.1 俯仰振荡支架干扰影响图 6中给出了ψ=0°、φ=0°、f=0.8Hz时俯仰振荡动静态试验支架干扰影响增量,图中看出法向力和俯仰力矩的动态支架干扰增量偏离静态支架干扰增量,而轴向力动态支架干扰增量在静态支架干扰增量附近小幅波动。
|
| 图 6 俯仰振荡纵向动静态试验支架干扰增量(ψ=0°,φ=0°,f=0.8Hz) Fig. 6 Interference quantities of longitudinal test results (ψ=0°,φ=0°,f=0.8Hz) |
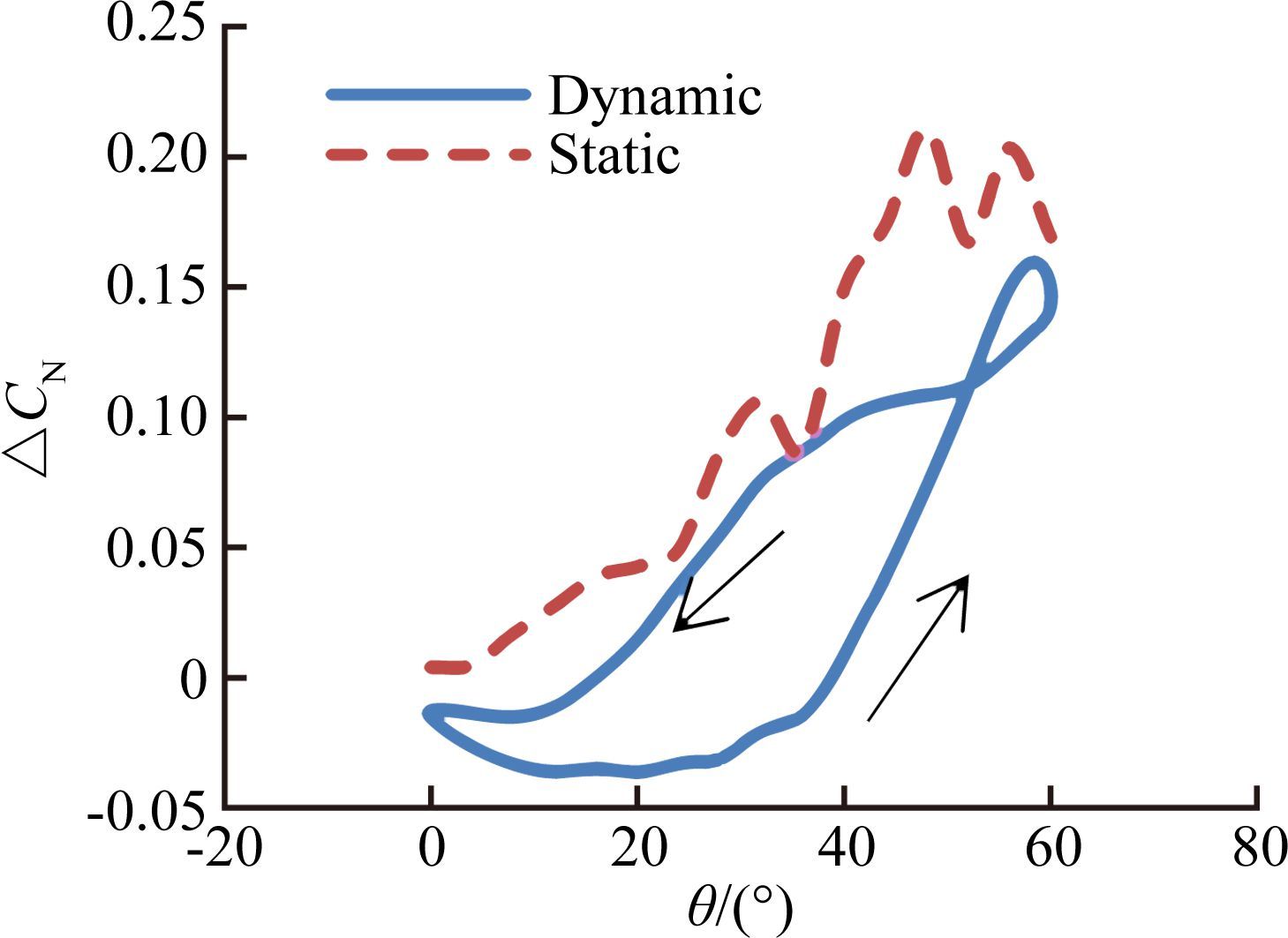
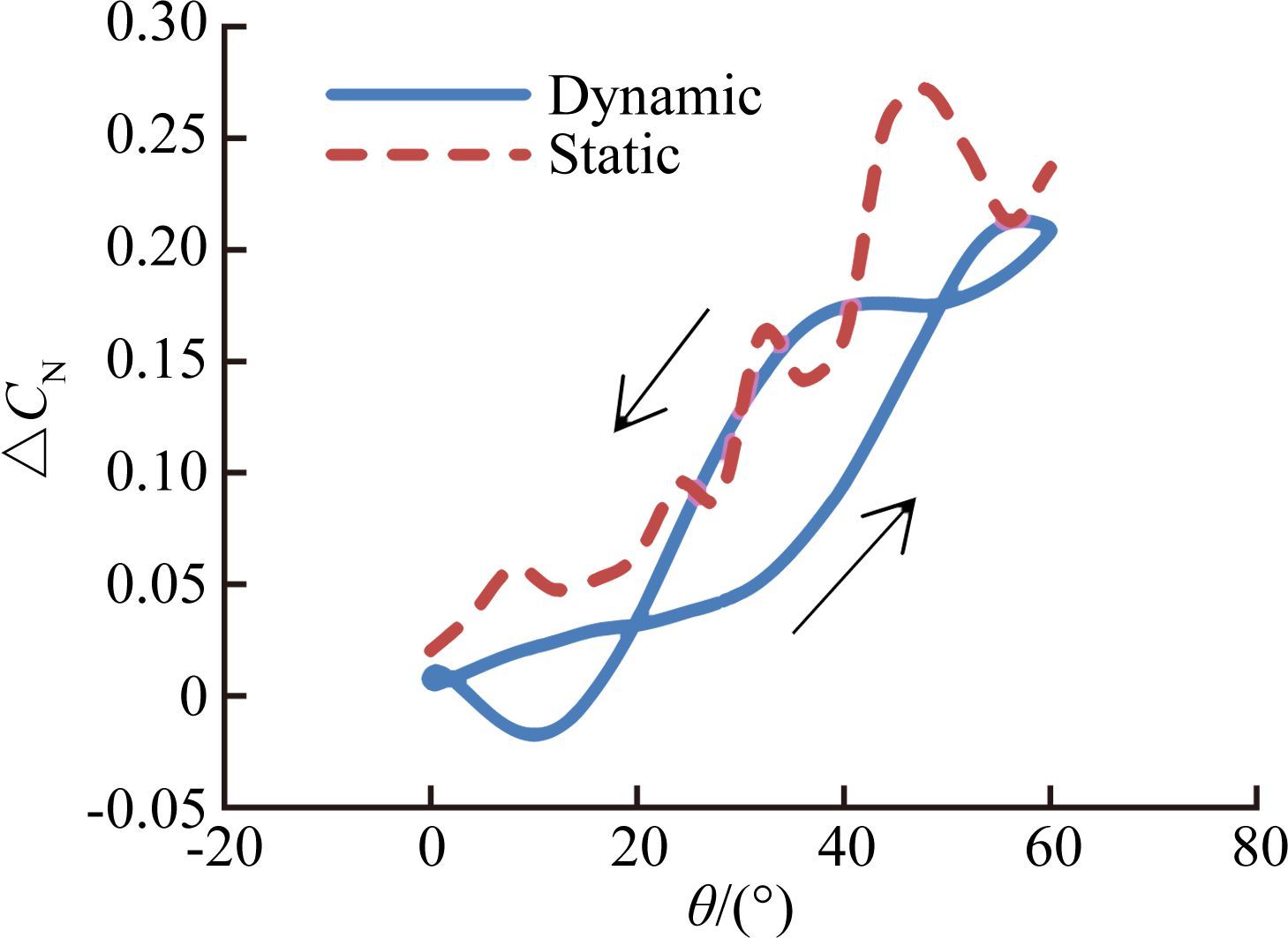
图 7、图 8给出了ψ=10°、ψ=20°(φ=0°,f=0.8Hz)时俯仰振荡纵向动静态试验支架干扰增量。通过图 6~图 8中不同偏航机构角的试验结果分析发现,随着偏航角的增大,动态支架干扰增量偏离静态支架干扰量的偏离值逐渐缩小,并静态增量逐渐回到动态增量迟滞环内。分析认为,偏离的原因可能是位于侧面的支撑系统对动态数据影响较大,随着支撑系统转到模型后方,影响量逐渐减小。
|
| 图 7 俯仰振荡纵向动静态试验支架干扰增量 (ψ=10°,φ=0°,f=0.8Hz) Fig. 7 Interference quantities of longitudinal test results (ψ=10°,φ=0°,f=0.8Hz) |
|
| 图 8 俯仰振荡纵向动静态试验支架干扰增量(ψ=20°,φ=0°,f=0.8Hz) Fig. 8 Interference quantities of longitudinal test results (ψ=20°,φ=0°,f=0.8Hz) |
法向力静态支架干扰增量在θ=0°~60°范围内均为正值,波动较小,并在θ=48°附近达到最大值0.17。当θ<48°时,随支杆俯仰角的增加而逐渐增大,随后随支杆俯仰角的增加逐渐减小。
在θ=0°~60°内,上仰过程中,法向力动态支架干扰增量随支杆俯仰角的增加逐渐降低,但绝对差量逐渐增加,在支杆俯仰角为29°时达到最低点-0.056。支杆俯仰角大于29°之后法向力动态支架干扰增量随支杆俯仰角增加而逐渐增大,在支杆俯仰角44°附近与横向坐标轴交叉,随后继续增大到俯仰角60°时的值0.68,在这一过程中绝对差量先减小到零,然后逐渐增大,意味着带支架和不带支架的动态数据在上仰过程中有一次交叉。
下俯过程中,法向力动态支架干扰增量随支杆俯仰角的变化规律与上仰过程相似,差别在于下俯过程中增量变化幅值较小,在18°附近达到负向最大值-0.036。另外带支架和不带支架的动态数据在下俯过程中也有一次交叉,但与上仰过程相比,交叉点的支杆俯仰角较小,在34°附近。
轴向力动静态支架干扰增量在迎角θ=0°~60°范围内均围绕横向坐标轴波动,波动幅度较小,在±0.006以内。
俯仰力矩静态支架干扰增量在θ=0°~32°内随支杆俯仰角单调减小,在32°时达到最小值-0.012,在θ=32°~60°范围内俯仰力矩呈波动下降趋势。俯仰力矩动态支架干扰增量,上仰和下俯过程中在支杆俯仰角小于49°时均呈单调递减趋势,随着支杆俯仰角的继续增大,俯仰力矩支架干扰增量开始增加。
图 9中给出俯仰振荡频率0.4Hz时纵向动静态支架干扰增量,图中可以看出与0.8Hz比较,上仰和下俯过程中支架对纵向分量的的影响规律基本一致,差别在于,上仰和下俯过程中支架干扰增量形成的迟滞环更小,趋近于粘合。
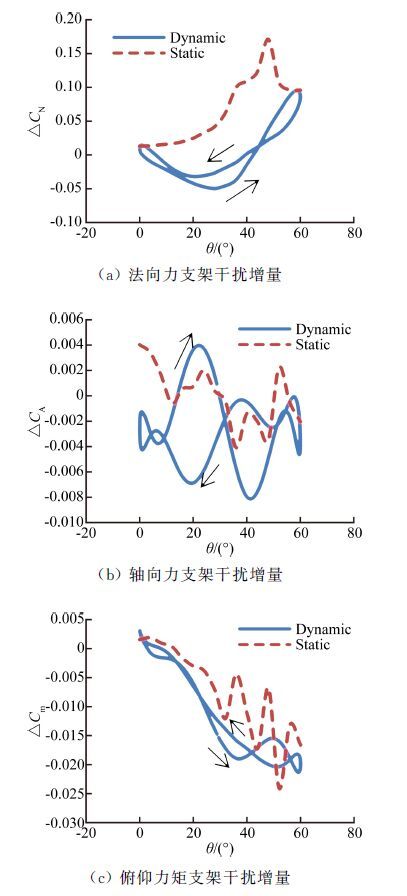
|
| 图 9 俯仰振荡纵向动静态试验支架干扰增量(ψ=0°,φ=0°,f=0.4Hz) Fig. 9 Interference quantities of longitudinal test results (ψ=0°,φ=0°,f=0.4Hz) |
综上所述,俯仰振荡试验中上仰和下俯过程中支架干扰的影响趋势相似,支架对法向力和俯仰力矩影响较大,对轴向力影响较小。随着频率的增加,纵向支架干扰增量在上仰和下俯运动过程中形成的迟滞环呈增大趋势。
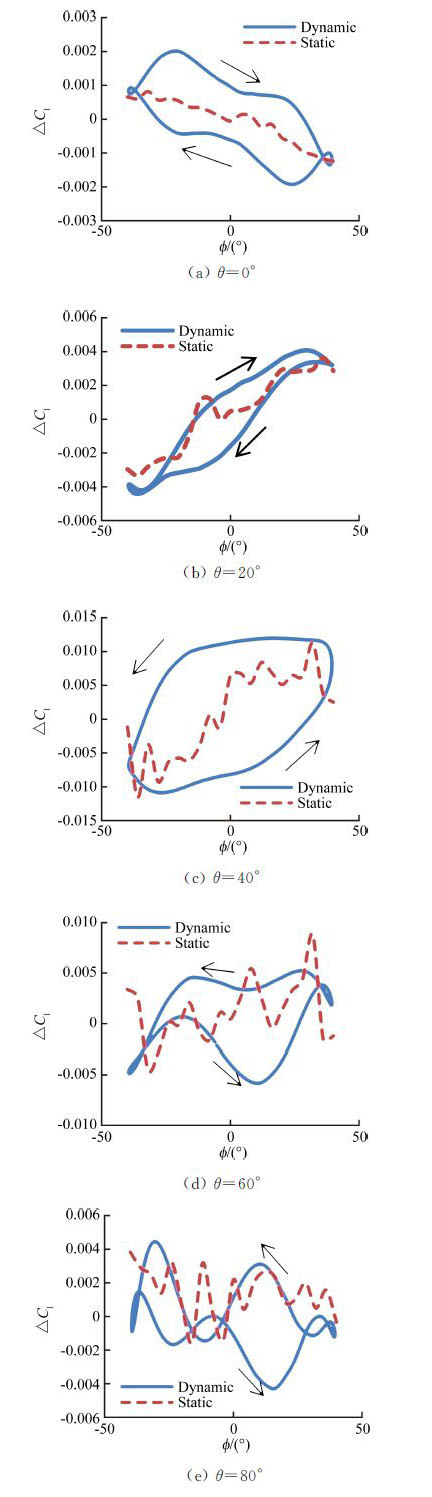
3.2 滚转振荡支架干扰影响图 10中给出了不同支杆俯仰角状态下动静态滚转振荡试验中滚转力矩支架干扰增量随滚转角变化曲线。图 10中可以看出各支杆俯仰角下静态增量基本全在动态增量迟滞环内,随着支杆俯仰角的增加,动静态滚转力矩支架干扰增量的极大值呈先增大后减小的趋势,并在支杆俯仰角40°时极大值达到0.012。
|
| 图 10 滚转振荡横向动静态试验支架干扰增量(ψ=0°,f=1.5Hz) Fig. 10 Interference quantities of lateral test results (ψ=0°,f=1.5Hz) |
在不同支杆俯仰角下,静态滚转力矩支架干扰增量随滚转角呈单调变化。θ=0°~40°范围内,随着支杆俯仰角的增加,静态滚转力矩支架干扰增量曲线斜率逐渐增加;θ=40°~80°范围内,随着支杆俯仰角的增加,静态滚转力矩增量曲线斜率开始逐渐减小。动态试验中滚转力矩支架干扰增量迟滞环也随静态滚转力矩支架干扰增量斜率变化而同向变化。
动态滚转力矩支架干扰增量迟滞环的变化趋势在0°支杆俯仰角时为顺时针方向,当支杆俯仰角增大到40°时迟滞环方向变为逆时针方向,之后到支杆俯仰角80°一直为逆时针变化规律。
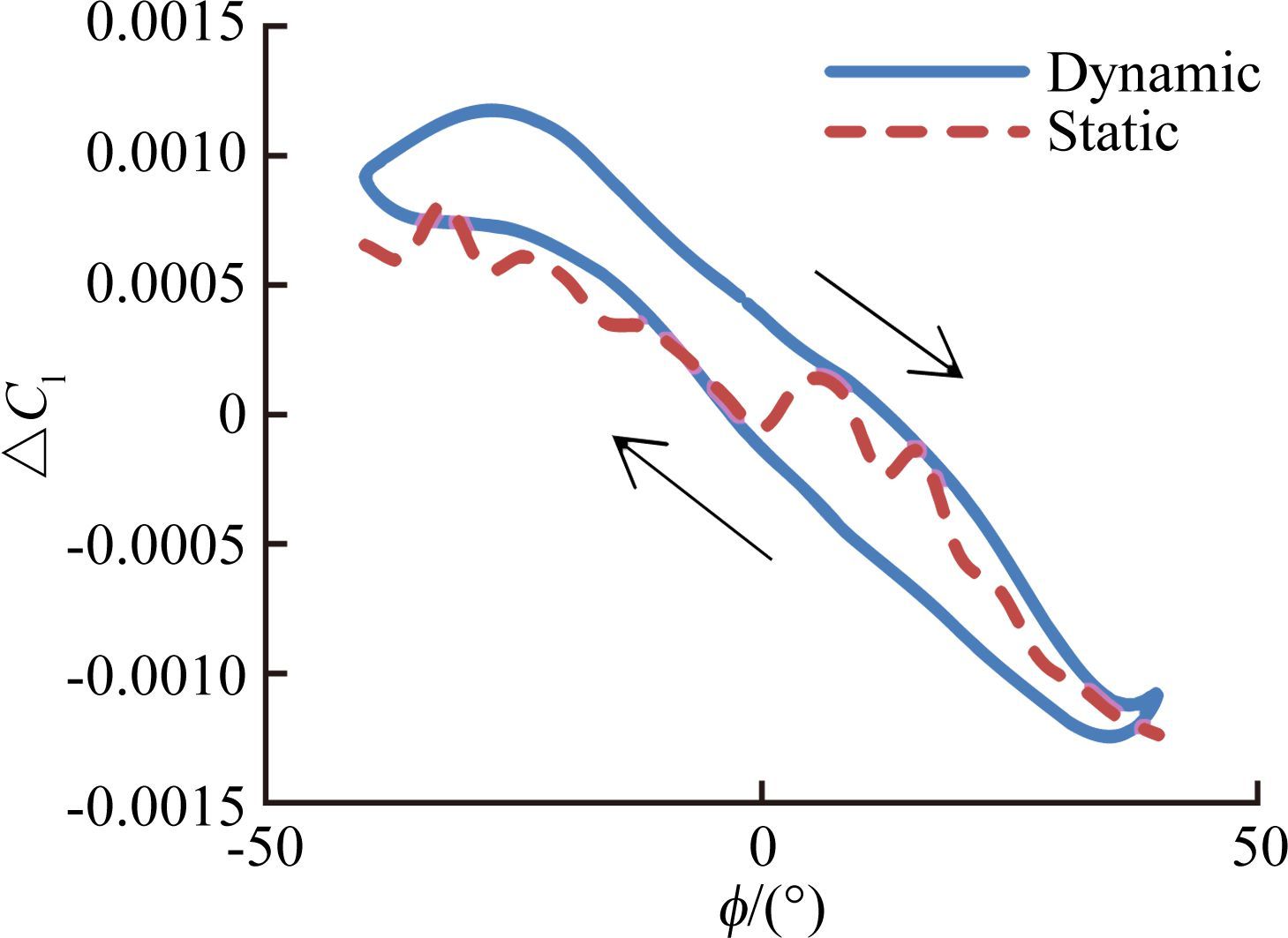
图 11中给出滚转振荡频率0.6Hz动静态支架干扰滚转力矩增量。从图 11中可以看出,与图 9(1.5Hz)比较,支架干扰影响规律基本一致,差别在于,迟滞环面积变小。
|
| 图 11 滚转振荡横向动静态试验支架干扰增量(ψ=0°,f=0.6Hz) Fig. 11 Interference quantities of lateral test results(ψ=0°,f=0.6Hz) |
综上所述,滚转振荡支架干扰影响量随支杆俯仰角的增加呈先增加后减小趋势。随着频率的增加,动态滚转力矩支架干扰增量迟滞环增大。
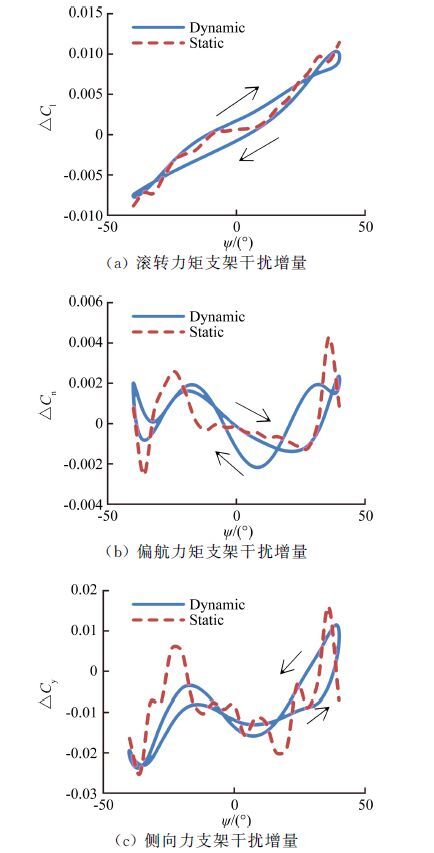
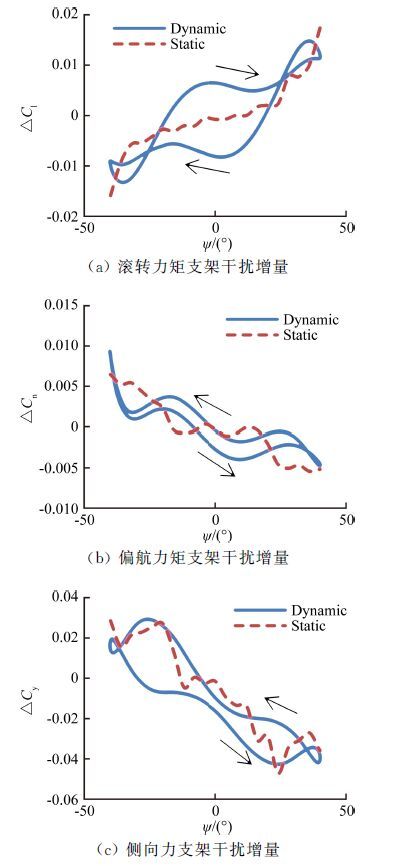
3.3 偏航振荡支架干扰影响图 12~图 14中给出了不同支杆俯仰角状态下动静态偏航振荡试验中横向三分量支架干扰增量随偏航机构角变化曲线。从图中可以看出,各支杆俯仰角下静态增量基本全在动态增量迟滞环内;随着支杆俯仰角的增加,动静态横向三分量支架干扰增量的极大值呈增大的趋势。
|
| 图 12 偏航振荡横向动静态试验支架干扰增量(θ=0°,φ=0°,f=0.8Hz) Fig. 12 Interference quantities of lateral test (θ=0° ,φ=0°,f=0.8Hz) |
|
| 图 13 偏航振荡横向动静态试验支架干扰增量(θ=20°,φ=0°,f=0.8Hz) Fig. 13 Interference quantities of lateral test results (θ=20°,φ=0°,f=0.8Hz) |
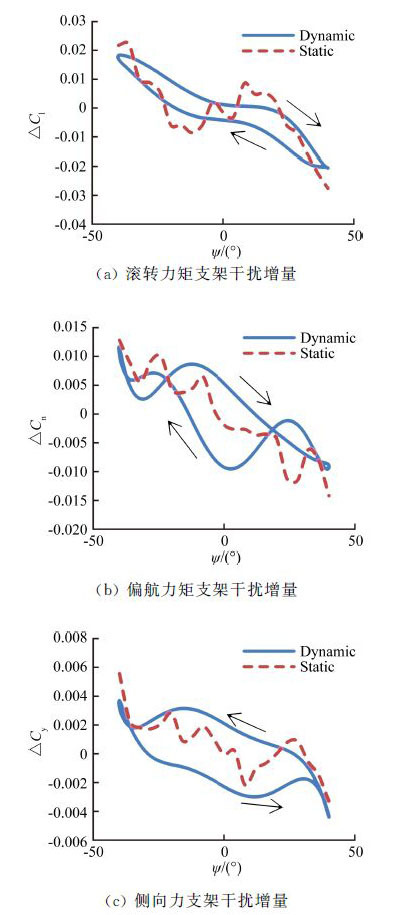
|
| 图 14 偏航振荡横向动静态试验支架干扰增量(θ=20°,φ=0°,f=0.8Hz) Fig. 14 Interference quantities of lateral test results (θ=20°,φ=0°,f=0.8Hz) |
在不同支杆俯仰角下,静态滚转力矩支架干扰增量随偏航机构角呈单调变化,偏航力矩和侧力支架干扰增量无明显变化规律。θ=0°~30°范围内,随着支杆俯仰角的增加,静态横向三分量支架干扰增量曲线斜率呈逐渐减小趋势,且偏航力矩和侧力支架干扰增量波动逐渐减小。动态试验中支架干扰增量迟滞环也随静态支架干扰增量斜率变化而同向变化。
动态横向三分量支架干扰增量迟滞环面积随支杆俯仰角增加而逐渐增大,说明偏航振荡时支杆俯仰角越大支架干扰越大。
图 15中给出偏航振荡频率0.4Hz动静态支架干扰滚转力矩增量。从图 14中可以看出,与图 13(0.8Hz)比较,支架干扰影响规律基本一致,但迟滞环面积变小。
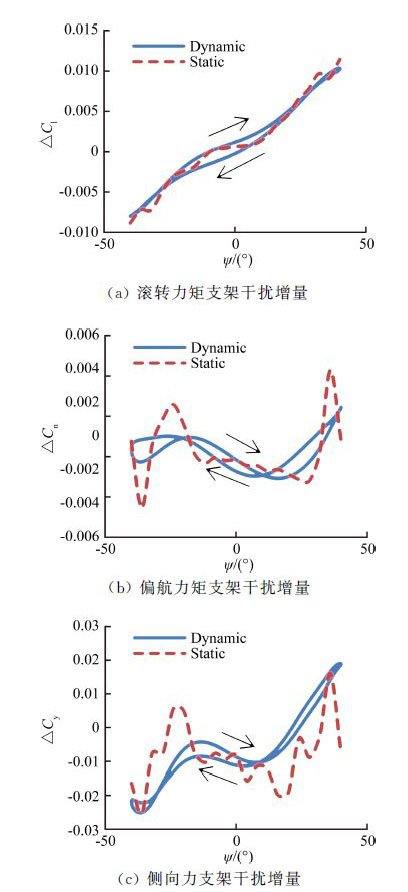
|
| 图 15 偏航振荡横向动静态试验支架干扰增量(θ=0°,φ=0°,f=0.4Hz) Fig. 15 Interference quantities of lateral test results (θ=0°,φ=0°,f=0.4Hz) |
综上所述,偏航振荡横向三分量支架干扰影响量随支杆俯仰角的增加呈增大趋势。随着频率的增加,动态横向三分量支架干扰增量迟滞环增大。
4 结 论通过两步法对俯仰、滚转和偏航三个模态的单自由度大幅振荡风洞试验的支架干扰进行了测量与分析,得出以下主要结论:
(1) 大幅振荡试验中支架干扰量随频率的增大而增大。
(2) 从俯仰振荡、偏航振荡和滚转振荡支架干扰试验结果来看,支架干扰对三类大幅振荡试验的准度影响较大,进行大幅振荡试验时,需要进行相应的支架干扰试验。
(3) 通过两步法进行大幅振荡支架干扰试验,可以去除支架的主要影响量,提高试验结果的准度,为飞机型号研制单位提供高准度试验数据,提高型号研制保障水平。
| [1] | Ericsson L E, Reding J P. Review of support interference in dynamic tests[J]. AIAA Journal, 1983, 21(12):1652–1666. DOI:10.2514/3.60166 |
| [2] | Ericsson L E, Reding J P. Dynamic support interference in high alpha testing[J]. Journal of Aircraft, 1986, 23(12):889–896. DOI:10.2514/3.45397 |
| [3] | Ericsson L E. Reflections regarding recent rotary rig results[J]. Journal of Aircraft, 1987, 24(1):25–30. DOI:10.2514/3.45406 |
| [4] | Ericsson L E. Another look at high-alpha support interference in rotary tests[J]. Journal of Aircraft, 1991, 28(9):584–591. DOI:10.2514/3.46068 |
| [5] | Lars E Ericsson, Martin E Byers. Aspects of ground facility interference on leading-edge vortex breakdown[J]. Journal of Aircraft, 2001, 38(2):310–314. DOI:10.2514/2.2763 |
| [6] | Beyers M E, Ericsson L E. Ground facility interference on aircraft configurations with separated flow[J]. Journal of Aircraft, 1993, 30(5):682–688. DOI:10.2514/3.46398 |
| [7] | Taylor G S, Gursul I, Greenwell D. Investigation of support interference in high-angle-of-attack testing[J]. Journal of Aircraft, 2003, 40(1):143–152. DOI:10.2514/2.3069 |
| [8] | Taylor G, Gursul I. Support interference for a maneuvering delta wing[J]. Journal of Aircraft, 2005, 42(6):1504–1515. DOI:10.2514/1.12094 |
| [9] |
Huang D, Wu G X. Experiment investigation of unsteady wall interference to model pitching in large angle of attack[J].
Journal of Nanjing University of Science and Technology, 2003, 27(4):349–354.
(in Chinese) 黄达, 吴根兴. 模型大振幅运动风洞壁面影响研究[J]. 南京理工大学学报, 2003, 27(4) : 349–354. |
| [10] |
Huang D, Zhang W H. Investigation on unsteady wind tunnel wall interference[J].
Acta Aerodynamica Sinica, 2004, 22(4):384–388.
(in Chinese) 黄达, 张文华. 非定常风洞洞壁干扰研究[J]. 空气动力学学报, 2004, 22(4) : 384–388. |
| [11] |
Huang D, Li Z Q, Ding K W, et al. Wall interference in unsteady force tests for delta wing in large amplitude pitching motions[J].
Journal of Nanjing University of Aeronautics and Astronautics, 2003, 35(1):13–17.
(in Chinese) 黄达, 李志强, 丁克文, 等. 三角翼大振幅俯仰运动非定常风洞动壁干扰实验研究[J]. 南京航空航天大学学报, 2003, 35(1) : 13–17. |
| [12] |
Li Z Q, Zhang W H, Huang Da, et al. Unsteady wind tunnel wall pressure research[J].
Acta Aeronautica et Astronautica Sinica, 1997, 18(6):652–655.
(in Chinese) 李志强, 张文华, 黄达, 等. 非定常风洞壁压特性研究[J]. 航空学报, 1997, 18(6) : 652–655. |
| [13] |
Zhang W H, Li Z Q, Ding K W, et al. Unsteady wall corrections for a delta wing oscillating in pitch to very high angles of attack[J].
Acta Aeronautica et Astronautica Sinica, 1997, 18(2):215–219.
(in Chinese) 张文华, 李志强, 丁克文, 等. 三角翼过失速非定常洞壁干扰修正[J]. 航空学报, 1997, 18(2) : 215–219. |
| [14] |
Du X Q. Investigation of support interference in low speed wind tunnel oscillation tests[J].
Experiments and Measurements in Fluid Mechanics, 2003, 17(2):37–40.
(in Chinese) 杜希奇. 动导数支架干扰的试验研究[J]. 流体力学实验与测量, 2003, 17(2) : 37–40. |
| [15] |
Gao J J, Liu C M, Bu C. Investigation of support interference on rotary balance test in FL-8 Low Speed Wind Tunnel[J].
Journal of Experiments in Fluid Mechanics, 2012, 26(1):88–92.
(in Chinese) 高剑军, 刘春明, 卜忱. FL-8风洞旋转天平试验支架干扰研究[J]. 流体力学实验与测量, 2012, 26(1) : 88–92. |


