2. 高速高雷诺数气动力航空科技重点实验室, 辽宁 沈阳 110034
2. Aero Science Key Lab of High Reynolds Aerodynamic Forces at High Speeds, Shenyang Liaoning 110034, China
结冰会对飞机飞行安全构成严重威胁。我国运输类飞机适航规章[1]、美国联邦航空规章(Federal Aviation Regulation,FAR)第25部[2]等对运输类飞机在结冰条件下的运行都有严格的要求。如果申请带有防冰设施的合格审定,飞机必须能在适航规章规定的连续和间断最大结冰状态下安全运行。
在飞机飞行的不同阶段,就结冰对飞机性能和操纵品质的影响来说都有一个临界冰形,它是在特定飞行阶段,在FAR 25部附录C规定的结冰条件内形成严重影响飞机性能和操纵品质的冰形[3]。“临界”通常用于表示对部件或系统产生最严重不利影响的情形[4]。AC(Advisory Circulars) 20-73A[5]对临界冰形的定义为:在适航规章结冰包线内,每个可用飞行构型下,对飞机操纵性和稳定性影响最严重的冰形。
对于飞机结冰问题而言,最严重影响一般指冰形导致升力损失最大,失速迎角减小最多,阻力增加最大,俯仰力矩变化最大等。因此若能验证飞机在临界冰形下的飞行安全,则一般可以确认飞机在结冰条件下的安全飞行性能。采用临界冰形还可以为飞机安全性能留以余量,以减小飞机和飞行员的安全风险。临界冰形的确定是飞机防除冰系统设计、适航取证等工作的重要内容。
Yoeman K 等人[6]利用经验公式的方法,分析了几何外形、飞行参数、结冰参数等对收集系数和结冰率的影响,与低温下的霜冰相比,在合适的环境温度、较小水滴直径以及相应液态水含量下形成的光冰对气动性能影响更为严重,可以判断为45min待机临界冰形。David C Parkins[7] 利用LEWICE结冰软件分析了某飞机在不同速度、迎角、温度、水滴直径下的结冰情况,并通过直观观察冰角厚度和角度等参数确定最严重的结冰状态。
近年来国内在飞机结冰及其影响的数值模拟方面开展了较多工作。北京航空航天大学常士楠[8]基于拉格朗日水滴轨迹追踪法和Messinger结冰热力学模型,建立了翼型表面结冰准定常数值模拟方法。中国空气动力研究与发展中心易贤[9]采用数值计算和结冰风洞试验相结合的手段,对某运输机机翼缩比翼型剖面的结冰特性进行了研究。中国 商飞上海飞机设计研究院冯丽娟[10]针对民 用飞机结冰适航取证工作,根据适航条款的结冰包线要求,结合飞机的飞行条件,提出了一种确定民用飞机严重结冰条件的方法。
临界冰形分析是飞机适航取证中的重要工作,本文对适航规章和咨询通告进行分析,发展基于数值模拟的临界冰形确定方法,并计算了待机构型下未防护表面45min临界冰形,讨论了临界冰形对飞机气动特性的影响。
1 临界冰形分析方法临界冰形分析应该综合考虑不同飞行阶段、不同表面防护状态、防除冰系统工作形式等。根据不同飞行阶段,可包括起飞结冰、起飞最后阶段结冰、航路结冰、待机结冰、进场结冰和着陆结冰,根据不同表面防护状态可分为防护面与未防护面,根据防除冰系统工作形式可分为正常工作、失效、延迟打开等。由于临界冰形的复杂性,通常要通过计算流体力学、冰风洞试验,甚至是自然结冰试飞等手段综合确定。根据AC 20-73A,FAR 25部附录C,最大连续结冰条件下的45min待机冰形是必须要考虑的临界冰形之一。本文主要研究基于CFD的45min待机临界冰形确定方法。
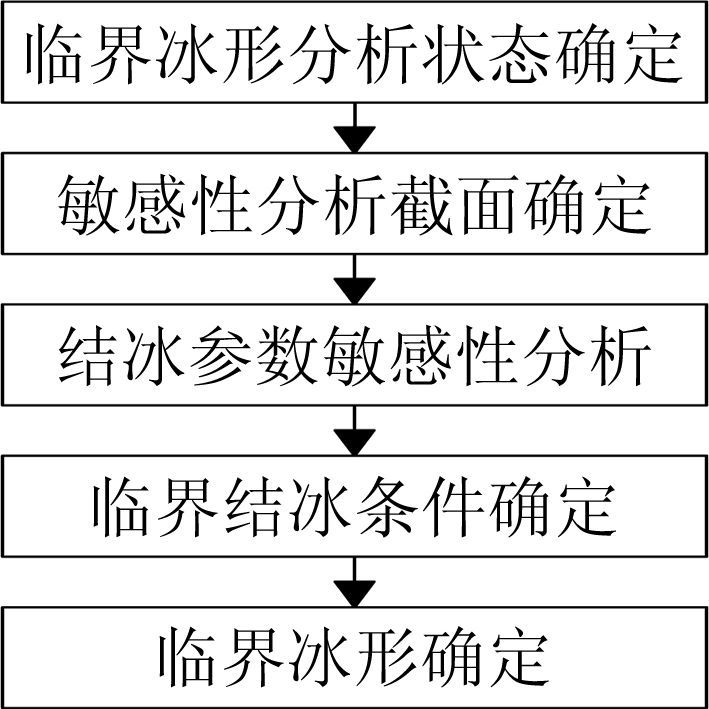
利用CFD方法计算临界冰形,一般可以分为临界冰形分析状态确定、敏感性分析截面确定、结冰参数敏感性分析、临界结冰条件确定、临界冰形确定等步骤,如图 1所示。其中临界冰形分析状态确定是指根据飞机飞行包线和结冰包线确定计算状态点,敏感性分析截面确定是指选择飞机翼面关键截面位置作为临界冰形确定的翼型,结冰参数敏感性分析是指分析结冰条件和飞行条件等不同参数对冰形的影响规律,临界结冰条件确定是指根据结冰参数敏感性分析结果确定临界结冰状态,临界冰形确定是指根据临界状态计算全机各处的冰形。
|
| 图 1 临界冰形分析流程图 Fig. 1 Critical ice shape analysis process |
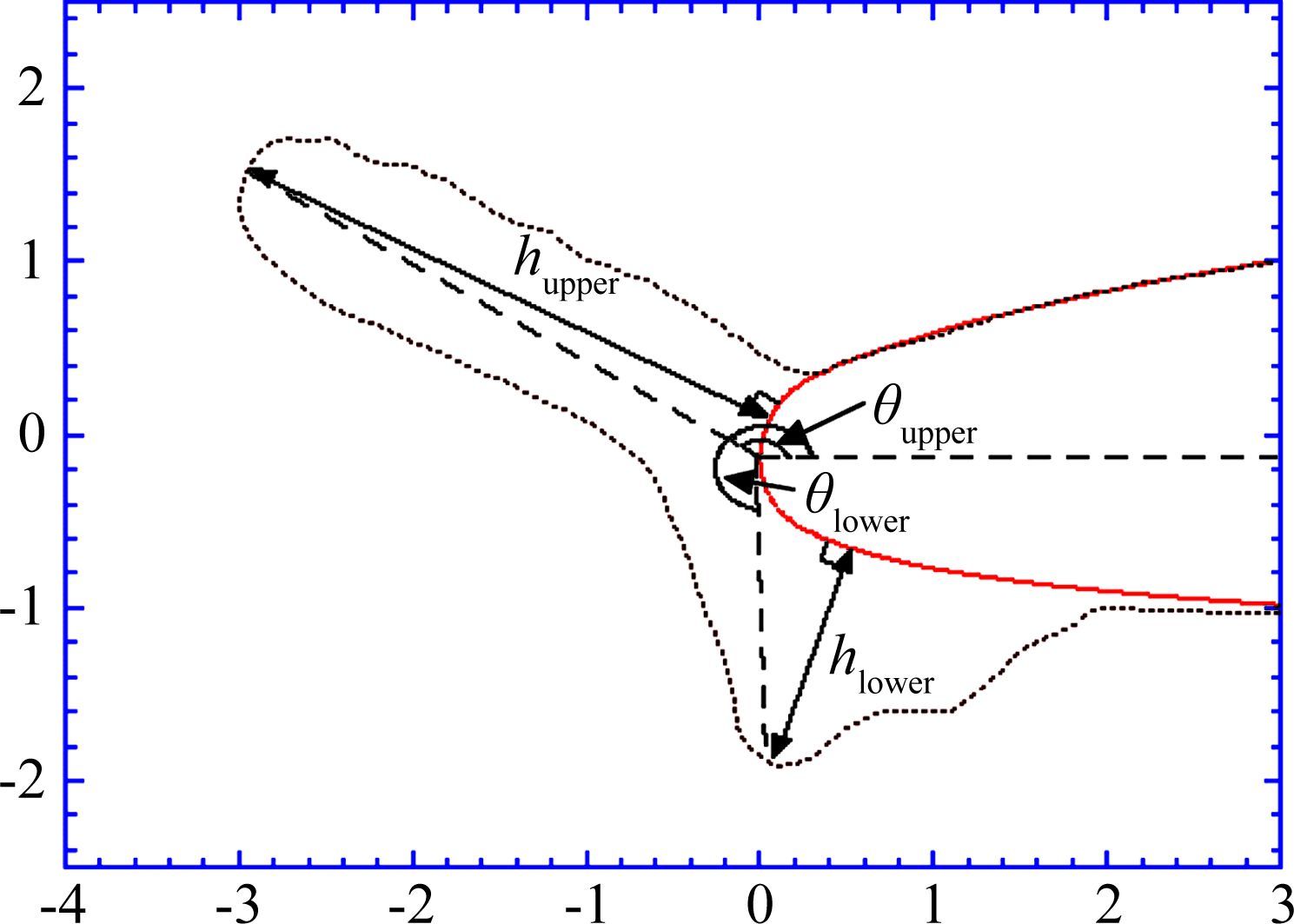
结冰参数敏感性分析过程中,需要从不同冰形中确定出最严重冰形,根据文献[11],可以用几何外形敏感性分析方法来进行。该方法根据冰形的上下冰角角度、冰角厚度等几何参数来确定最严重冰形。这些冰形参数的取值方法如图 2所示。冰角越向外张开,即上冰角角度θupper越小,下冰角角度θlower越大,对气动性能的影响越大;同时,上冰角厚度hupper和下冰角厚度hlower越大的冰形,对气动性能的影响就更为严重。该方法简单易行,但只能适用于冰角明显、位置相近、冰形相似的情况。
|
| 图 2 冰形几何参数示意图 Fig. 2 Definition of ice shape parameter |
2 数值模拟方法 2.1 流场计算方法
采用中航工业空气动力研究院气动力计算平台(UNSMB)计算流场。考虑质量、动量、能量的守恒,在一个体积为Ω的区域里N-S方程的积分形式为:
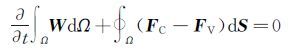
|
(1) |
式中 W 是守恒变量,F C是对流通量,F V是粘性通量。对式(1)采用Jameson中心格式的有限体积法进行空间离散,并用显式四步龙格-库塔方法进行时间离散。使用了当地时间步长、多重网格以及残值光顺等加速收敛技术。湍流模型为S-A一方程模型。
2.2 水滴计算方法在水滴撞击特性计算中,采用了Eulerian方法。水滴控制方程形式如下,其中α为水滴体积分数, u 为水滴速度, u a为空气速度,CD为水滴阻力系数,Red为水滴雷诺数,K为惯性因子,ρa为空气密度,ρ为水滴密度,Fr为Froude数,g为重力加速度,各项参数的具体计算方法参见文献[12]。
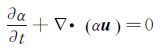
|
(2) |
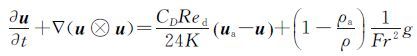
|
(3) |
采用 经典的Messinger结冰热力学模型来计算结冰过程。将结冰表面划分为若干控制体,通过求解控制体内如下形式的质量和能量方程得到每个控制体内的结冰量。其中$\dot{m}$ im为水滴撞击控制体带来的水流量,$\dot{m}$ in为前一个控制体流到当前控制体的水流量,$\dot{m}$ va为蒸发或升华产生的水蒸气 流量,$\dot{m}$ ou为流出控制体的水流量,$\dot{m}$ so为结冰量。$\dot{E}$ so表示控制体内水结冰所释放的能量,$\dot{H}$ va表示蒸发或者升华吸收的能量,$\dot{H}$ ou表示流出控制体的水带走的能量,$\dot{H}$ in表示流入控制体水带来的能量,$\dot{H}$ im表示制体内撞击水滴带来的能量,$\dot{Q}$ f表示空气与物面摩擦生热,$\dot{Q}$ c表示空气对流换热,各项参数的具体计算方法参见文献[13]。
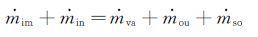
|
(4) |
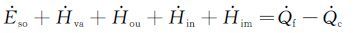
|
(5) |
为了验证结冰数值模拟方法的可靠性,将数值模拟结果与文献[14-15]中的试验结果进行了对比,结果表明水滴收集系数分布、最大收集系数、撞击范围、结冰外形、最大结冰厚度等均吻合良好。

|
| 图 3 计算与试验结果对比 Fig. 3 Comparison between simulation and test |
2.4 计算模型及网格
研究选用第四届AIAA阻力预测会中使用的CRM(Common Research Model)模型[16]。几何外形如图 4所示,未结冰构型计算网格如图 5所示。

|
| 图 4 CRM模型示意图 Fig. 4 Common Research Model (CRM) |
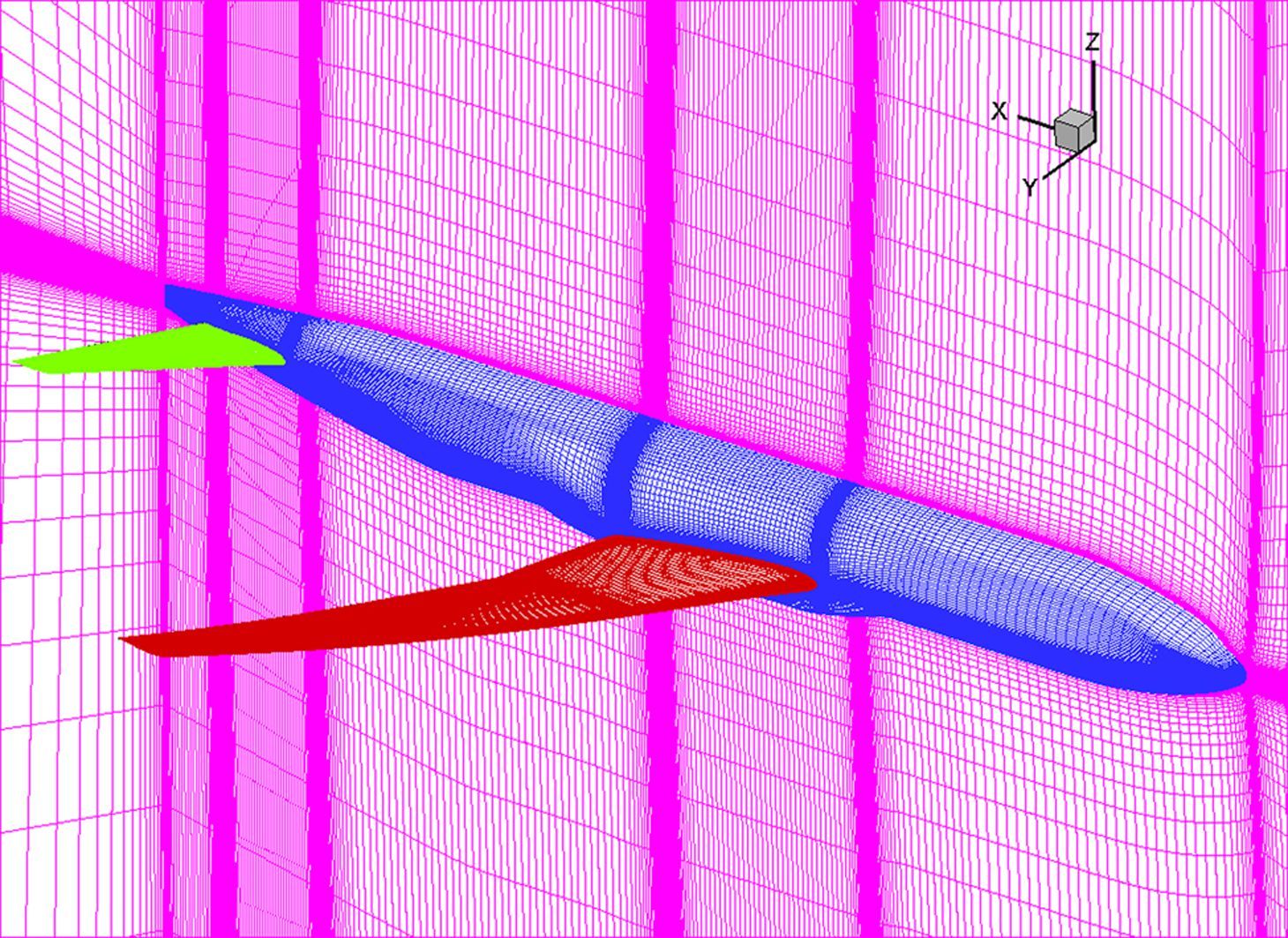
|
| 图 5 未结冰构型计算网格示意图 Fig. 5 Diagram of clean grid |
3 临界冰形计算分析
按前述的临界冰形分析方法,计算了CRM飞机未防护状态下45min待机临界冰形。参考FAR 25部附录C的结冰条件,确定临界冰形分析状态,如表 1所示。其中液态水含量(LWC)由FAR 25部附录C计算得出,速度、迎角、高度等参数均为假定的飞行参数。
| 状态 | 速度/(m·s-1) | 迎角/(°) | 高度/km | 静温/K | 水滴直径/μm | LWC/(g·m-3) | 结冰时间 /min |
| 1 | 120 | 3 | 5 | 266 | 20 | App.C | 45 |
| 2 | 120 | 3 | 5 | 264 | 20 | App.C | 45 |
| 3 | 120 | 3 | 5 | 262 | 20 | App.C | 45 |
| 4 | 120 | 3 | 5 | 259 | 20 | App.C | 45 |
| 5 | 120 | 3 | 5 | Critical | 40 | App.C | 45 |
| 6 | 120 | 3 | 5 | Critical | 30 | App.C | 45 |
| 7 | 120 | 3 | 5 | Critical | 20 | App.C | 45 |
| 8 | 120 | 3 | 5 | Critical | 15 | App.C | 45 |
| 9 | 100 | 5 | 5 | Critical | Critical | App.C | 45 |
| 10 | 110 | 4 | 5 | Critical | Critical | App.C | 45 |
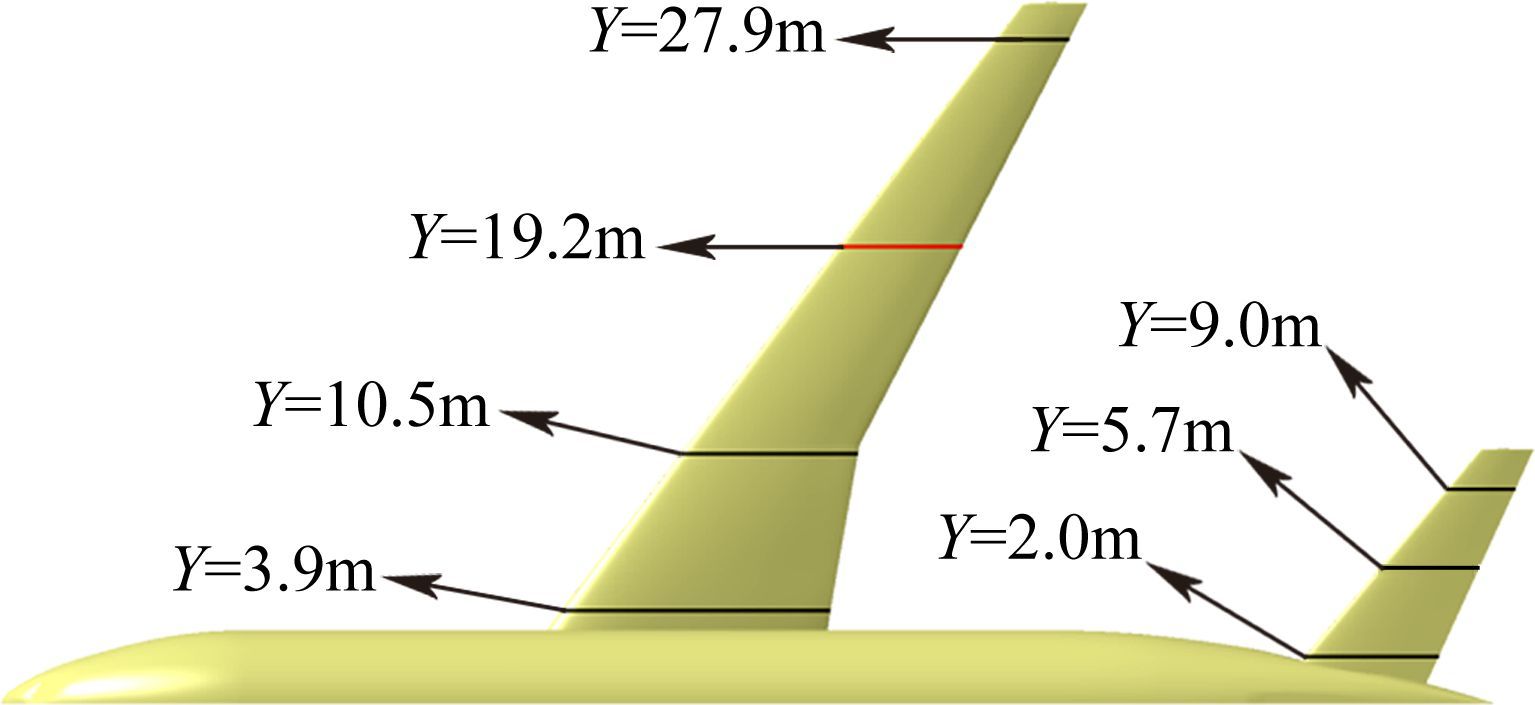
根据文献[6],敏感性分析截面通常选在操纵面附近、水平安定面、主翼外翼等位置。计算选取机翼外翼50%展长处作为敏感性分析截面(见图 6中红色标示截面),机翼截面站位Y=19.2m,其截面翼型外形如图 7所示。其余截面用于计算全机临界冰形,站位情况如表 2所示。
| 翼型名称 | 截面 | 敏感性分析 | 临界冰形 |
| 机翼 | Y=3.9m | - | √ |
| 机翼 | Y=10.5m | - | √ |
| 机翼 | Y=19.2m | √ | √ |
| 机翼 | Y=27.9m | - | √ |
| 平尾 | Y=2.0m | - | √ |
| 平尾 | Y=5.7m | - | √ |
| 平尾 | Y=9.0m | - | √ |
|
| 图 6 临界冰形分析站位示意图 Fig. 6 Selected cuts for critical ice shape calculation |

|
| 图 7 机翼Y=19.2m截面翼型 Fig. 7 Airfoil of Y=19.2m cut |
在选定的敏感性分析截面上,针对影响飞机结冰的温度、水滴直径、飞行条件等各类参数进行结冰敏感性分析,获得严重结冰条件。
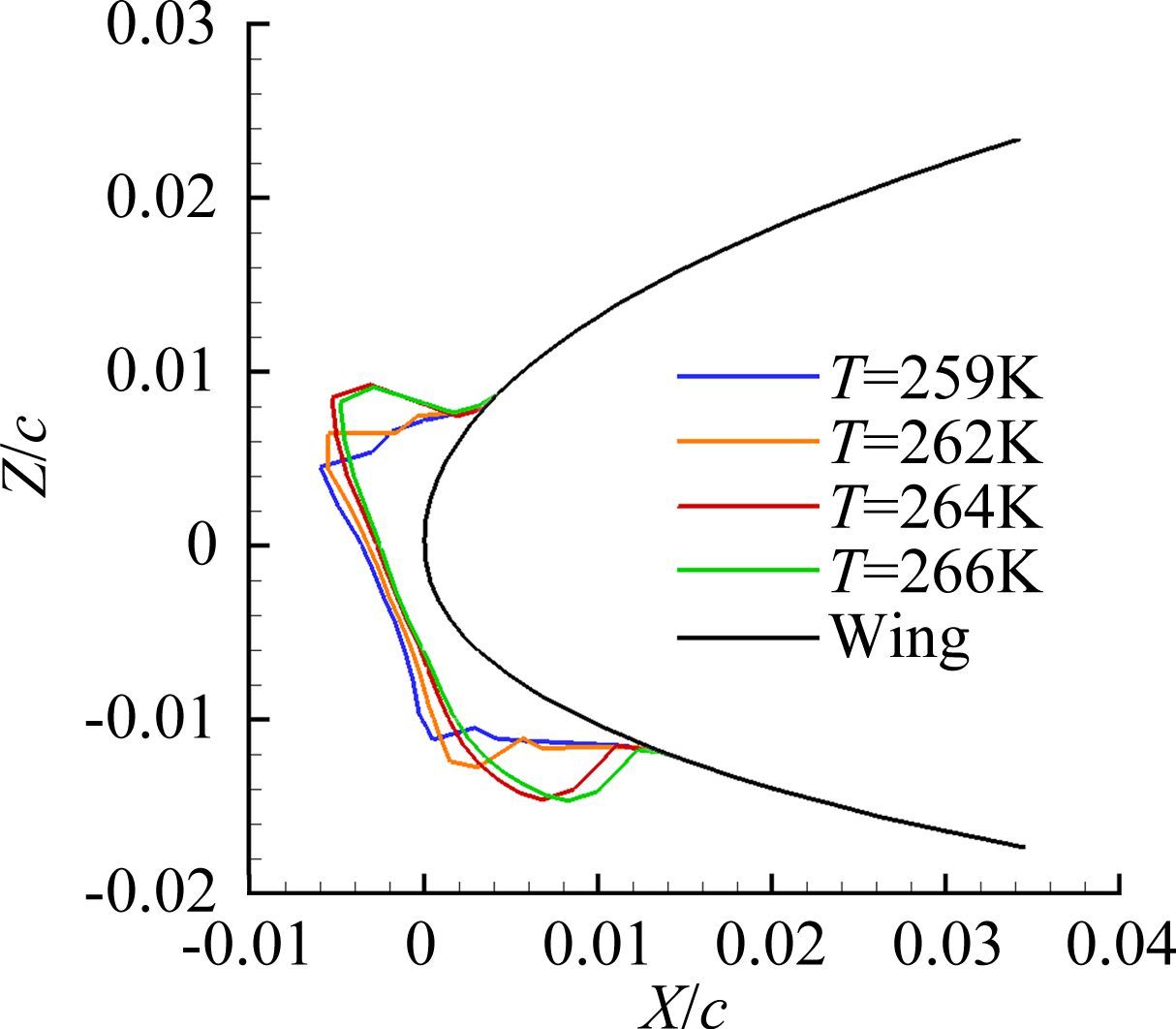
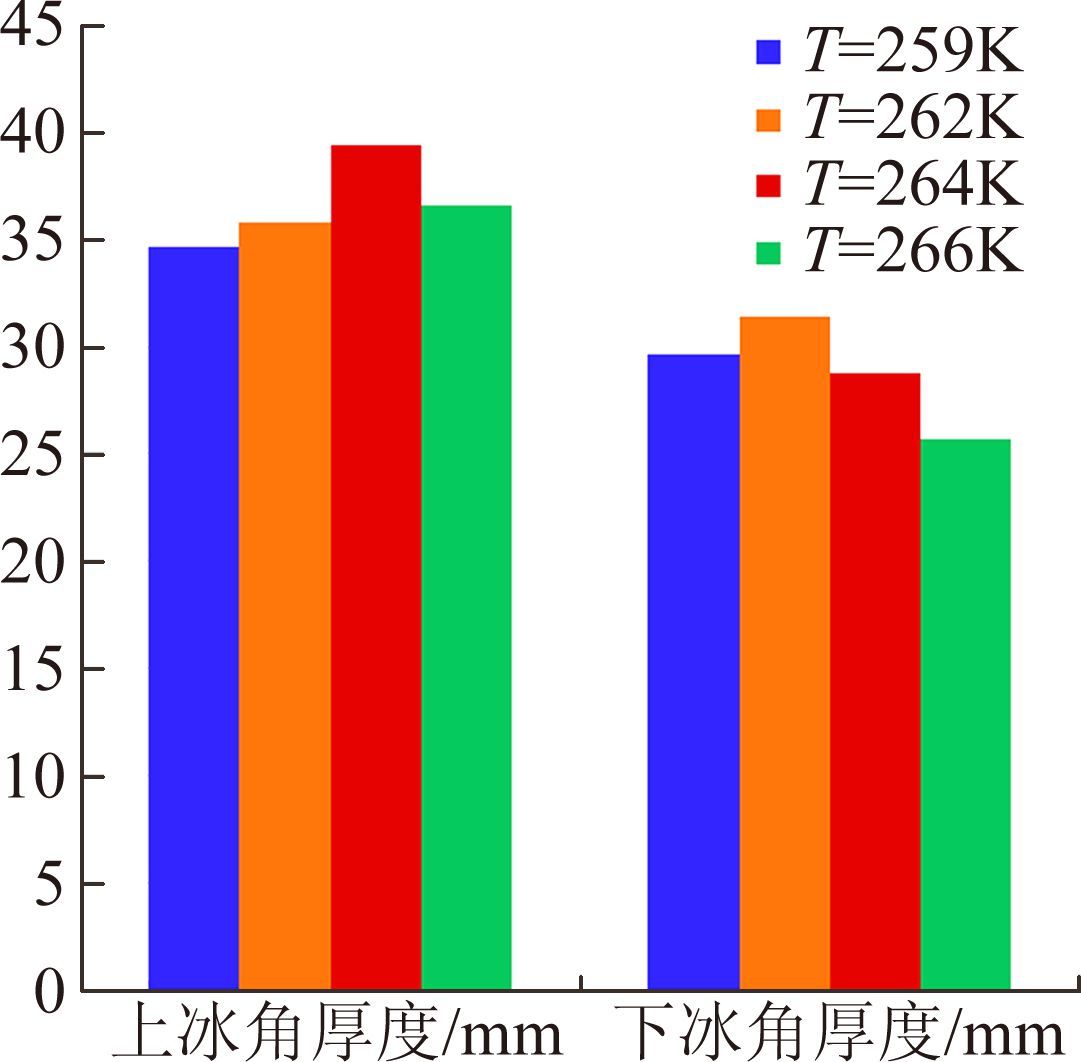
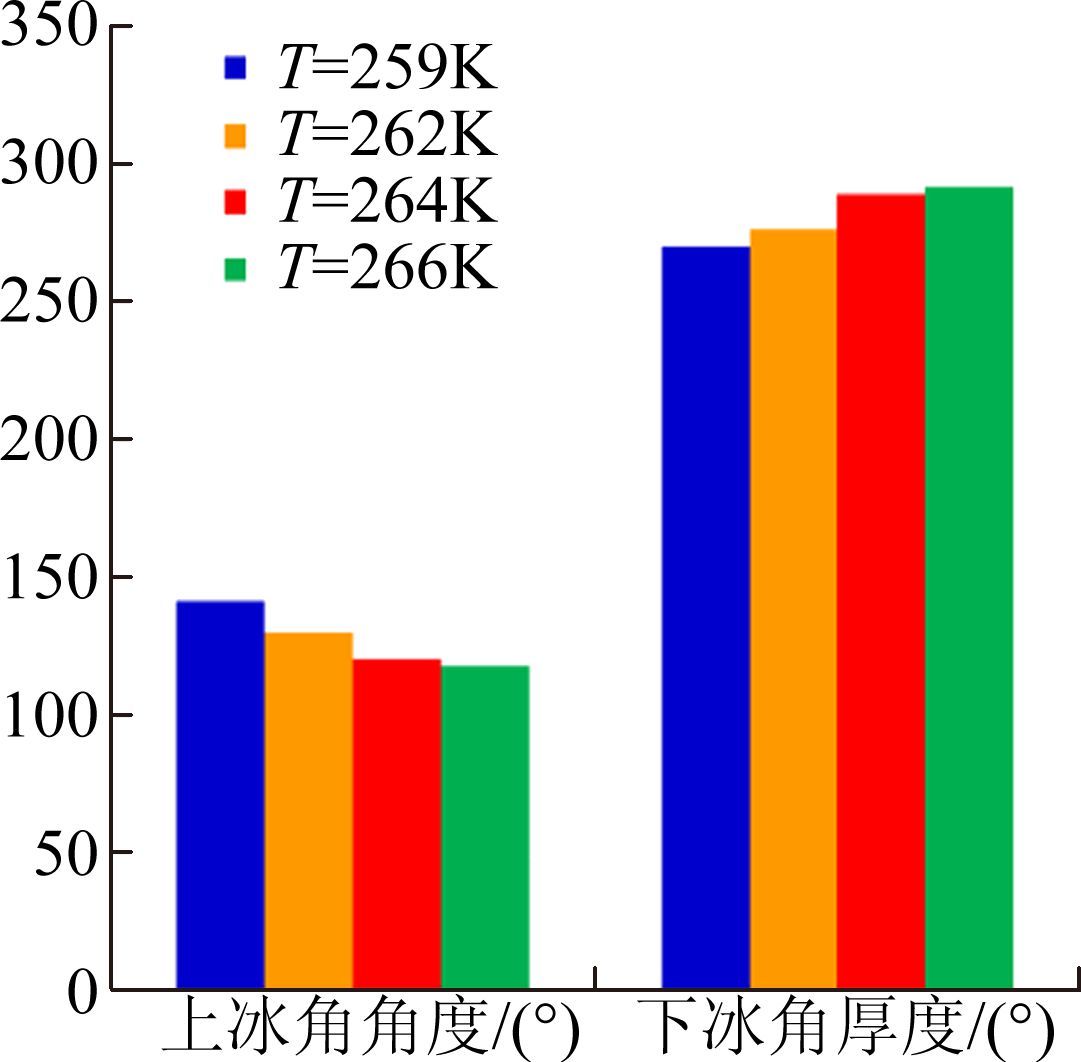
3.1 温度敏感性分析温度是影响飞机表面冰增长的最主要因素之一,是结冰形状的重要决定参数。进行机翼结冰敏感性分析时选取4种不同温度(如表 1中计算状态1~4)。图 8给出了不同温度下的冰形,冰角厚度和冰角角度如图 9和图 10。采用几何外形敏感性分析方法进行温度敏感性分析,通过对比发现,温度为264K时,上冰角厚度达到最大值约40mm,下冰角厚度和冰角角度等参数与其它温度下冰形差距不大。考虑到上冰角对气动性能影响更为主要,确定264K为最严重结冰温度。
|
| 图 8 不同温度冰形图 Fig. 8 Effect of temperature variations on ice shape |
|
| 图 9 不同温度冰形冰角厚度比较 Fig. 9 Comparison of ice horn maximum thickness with different temperatures |
|
| 图 10 不同温度冰形冰角角度比较 Fig. 10 Comparison of ice horn angle with different temperatures |
3.2 水滴直径敏感性分析
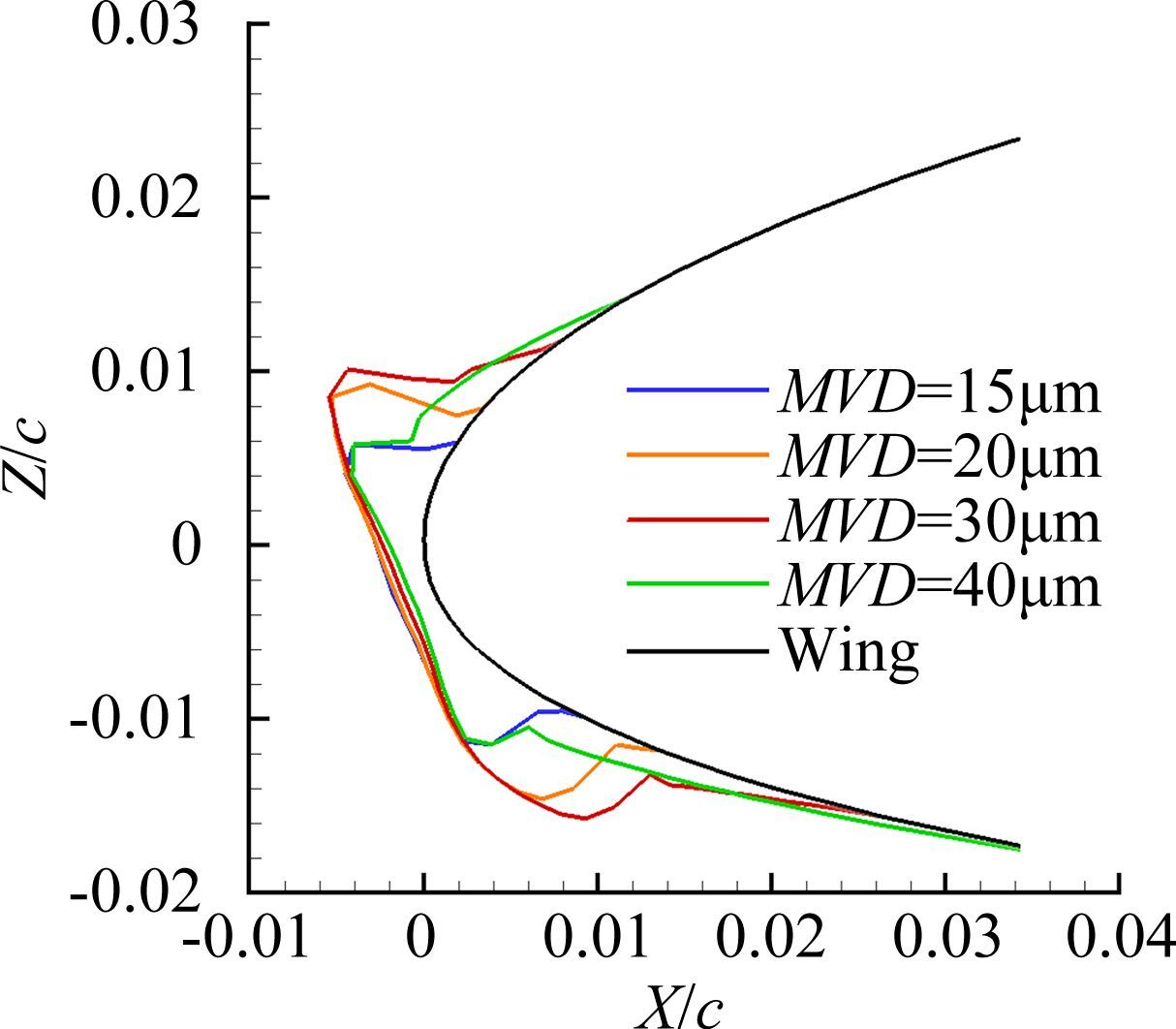
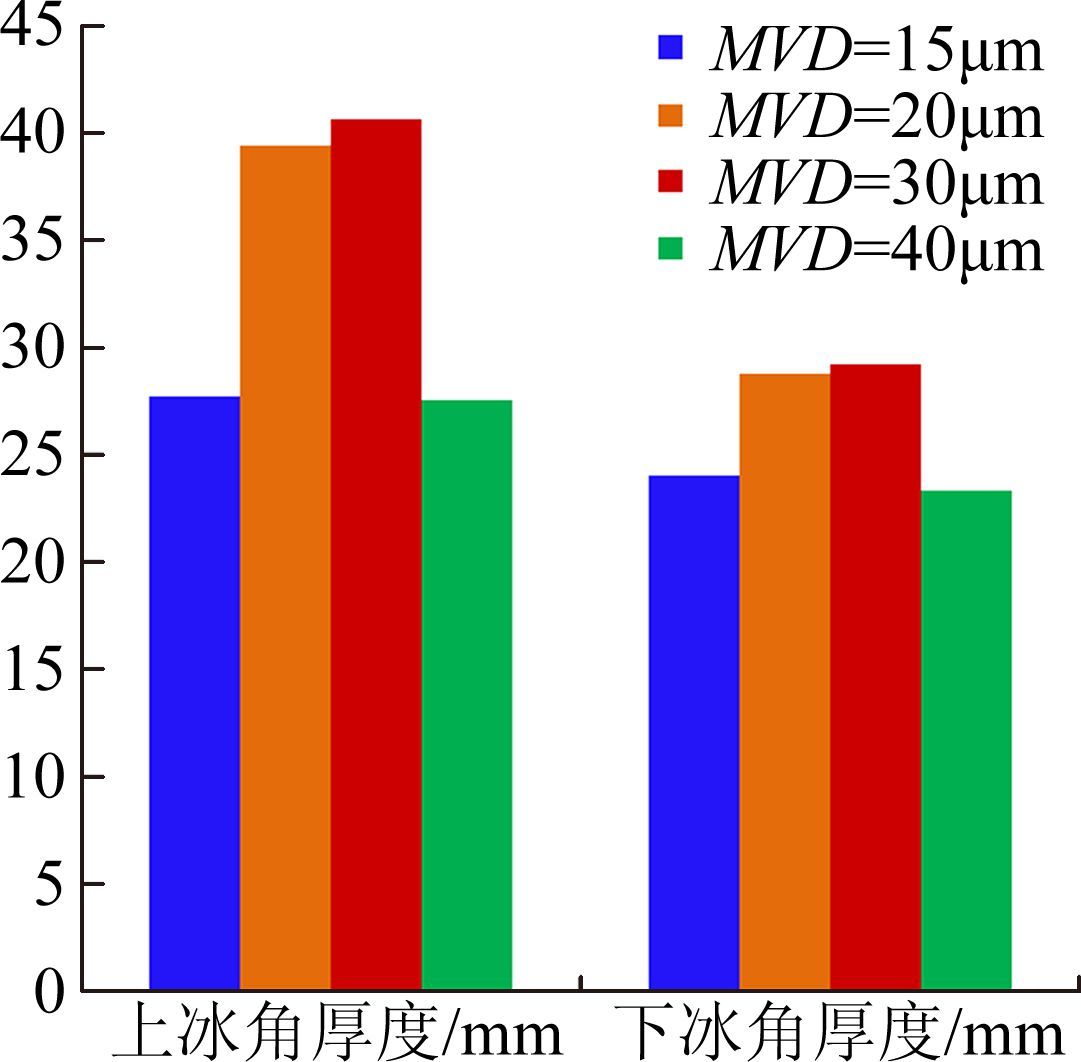
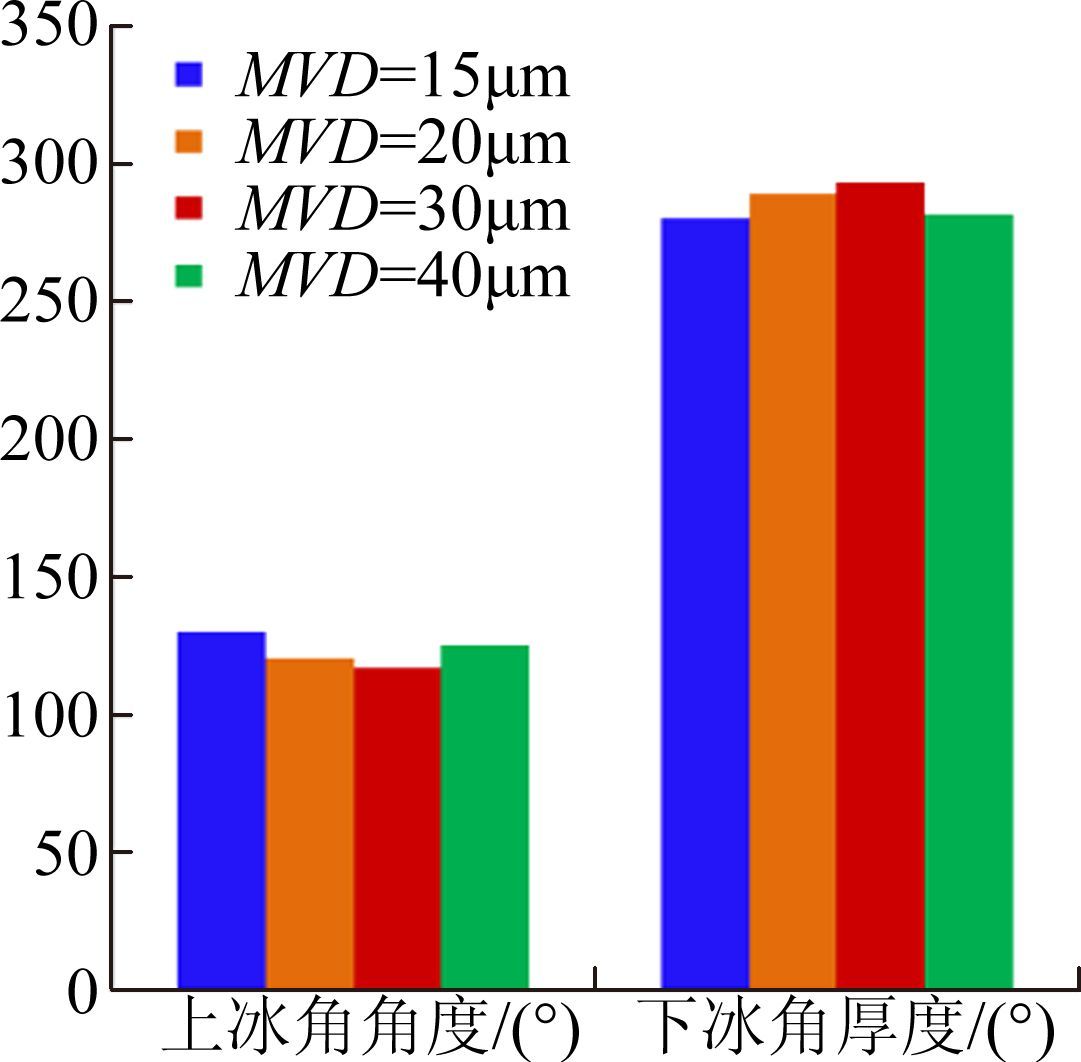
水滴直径是重要的云雾参数,对结冰范围、冰厚、角度等都有较大的影响。基于确定的最严重结冰温度,选取4种不同尺寸的水滴直径(如表 1中计算状态5~8),进行结冰计算,比较获得结冰最严重水滴直径。图 11给出了不同水滴直径下的冰形。冰角厚 度和冰角角度见图 12和图 13。通过对比发现,在水滴直径为30μm时上冰角厚度和下冰角厚度最大,冰角最大厚度达到约41mm,并且上冰角角度最小,下冰角角度最大,为最严重结冰水滴直径。
|
| 图 11 不同水滴直径冰形图 Fig. 11 Effect of droplet diameter variations on ice shape |
|
| 图 12 不同水滴直径冰形冰角厚度比较 Fig. 12 Comparison of ice horn maximum thickness with different droplet diameters |
|
| 图 13 不同水滴直径冰形冰角角度比较 Fig. 13 Comparison of ice horn angle with different droplet diameters |
用与上述类似的方法,还对不同飞行条件的结冰敏感性进行了分析。基于确定的最严重环境温度和最严重水滴直径,选取3种不同飞行状态进行飞行条件敏感性分析(如表 1中计算状态9~10,其中结冰参数为之前确定的最严重环境温度和水滴直径)。通过对比得到最严重结冰条件为:飞行高度5km,速度120m/s,迎角3°。
3.3 临界冰形的确定通过结冰参数敏感性分析工作,确定了CRM飞机待机构型下45min临界结冰条件,如表 3所示。
| 速度/(m·s-1) | 迎角/(°) | 高度/km | 温度/K | 水滴直径/μm |
| 120 | 3 | 5 | 264 | 30 |
根据分析得出的临界结冰条件,可以计算得到飞机各截面的临界冰形,如图 14所示。

|
| 图 14 各截面处临界冰形 Fig. 14 Critical ice shapes |
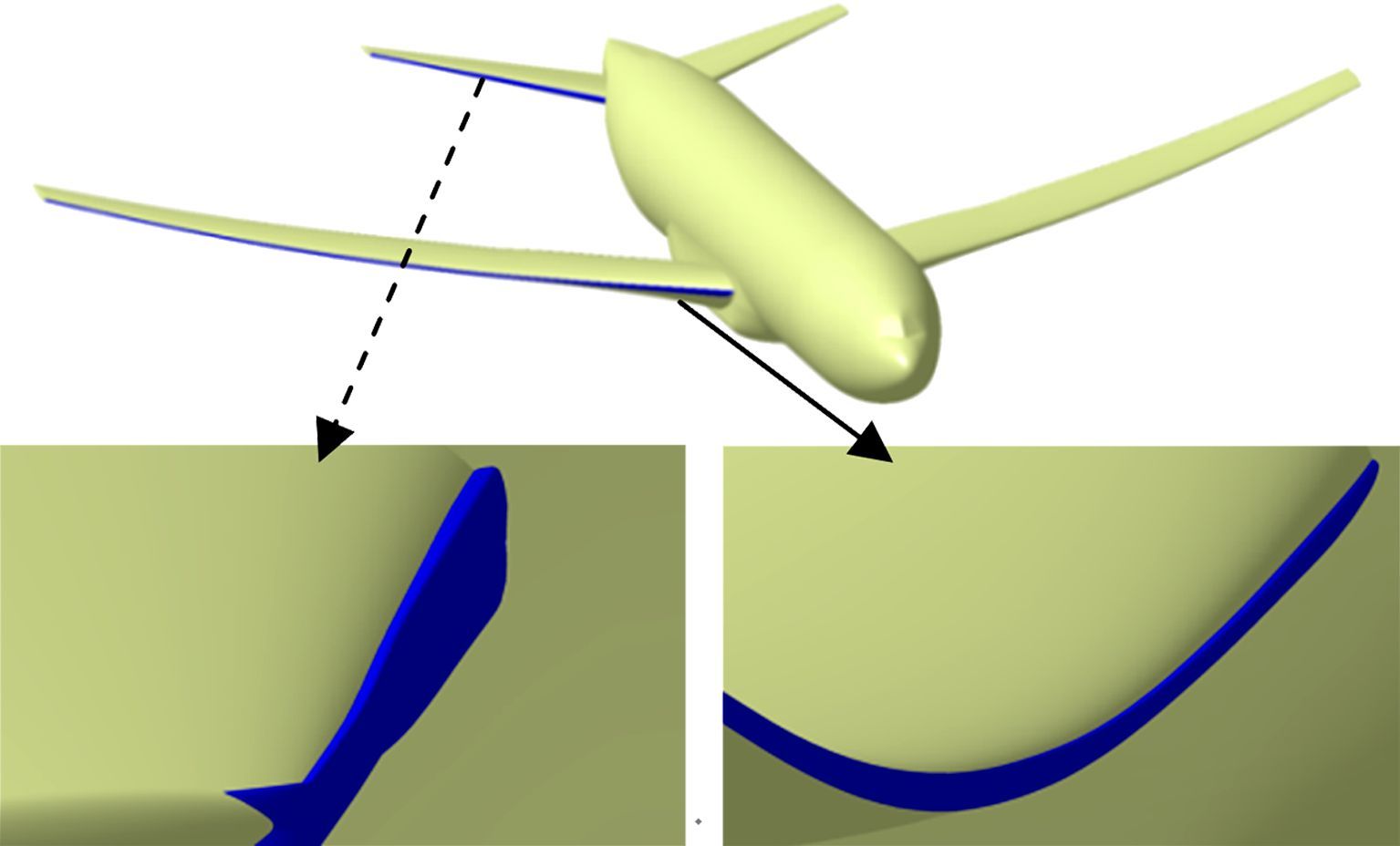
以机翼和平尾各截面临界冰形为基准,通过三维建模方法可以得到全机三维临界冰形,可用于结冰后气动性能评估,如图 15所示。
|
| 图 15 CRM待机构型45min临界冰形 Fig. 15 45 minutes holding critical ice shape |
4 临界冰形对气动性能影响分析
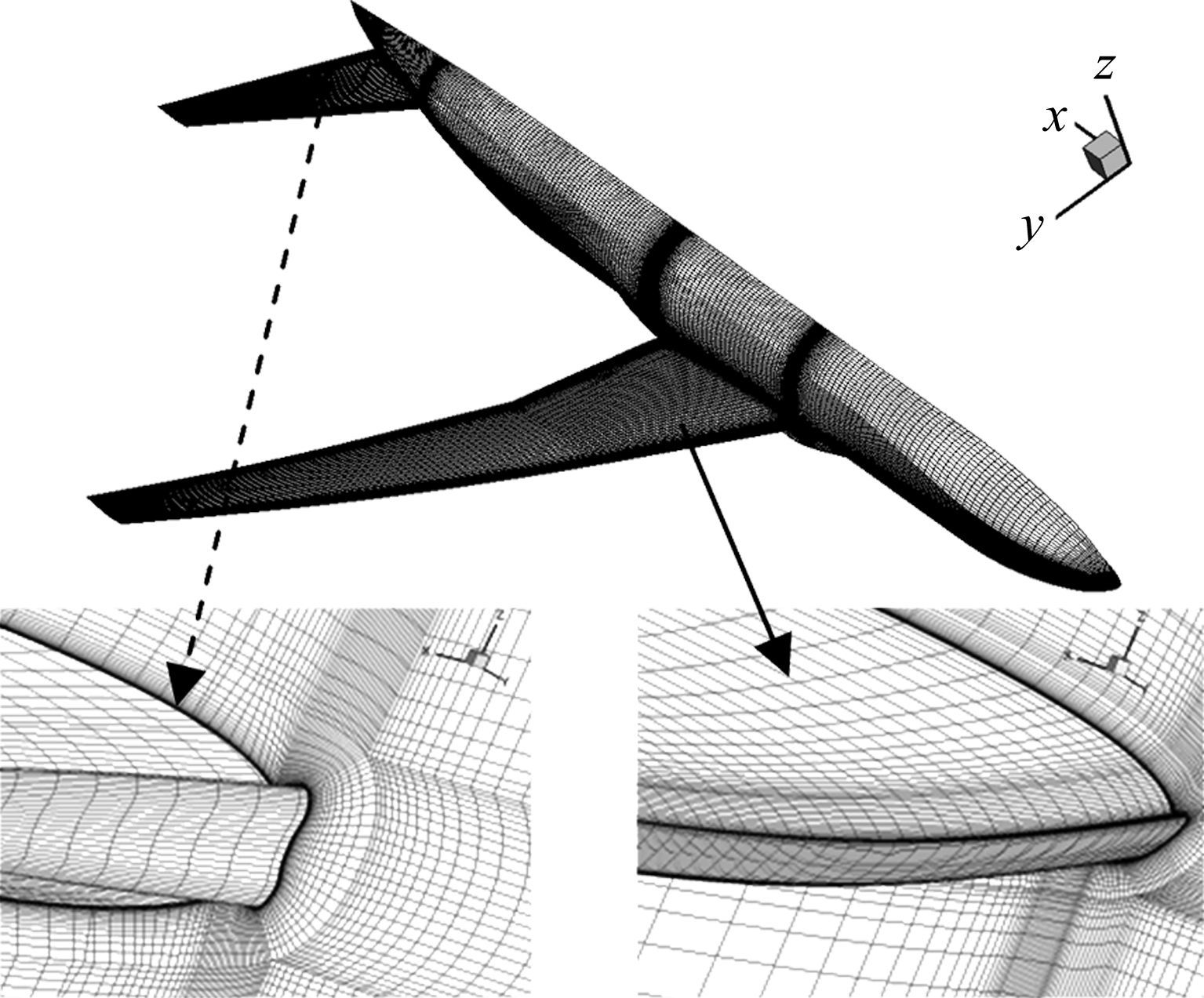
在确定了临界冰形后,采用CFD方法对结冰后飞机气动性能进行评估,计算状态见表 4,计算网格如图 16。得到结冰状态下飞机的升力、阻力特性以及俯仰力矩系数,见图 17、图 18以及表 5。
| 网格 | Ma | 高度/km | 迎角/(°) |
| 未结冰 | 0.4 | 5 | 0,3,5,7,8,9,10 |
| 带冰 | 0.4 | 5 | 0,3,5,6,7,8,9 |
|
| 图 16 三维带冰网格图 Fig. 16 Diagram of grid in consideration of icing |
|
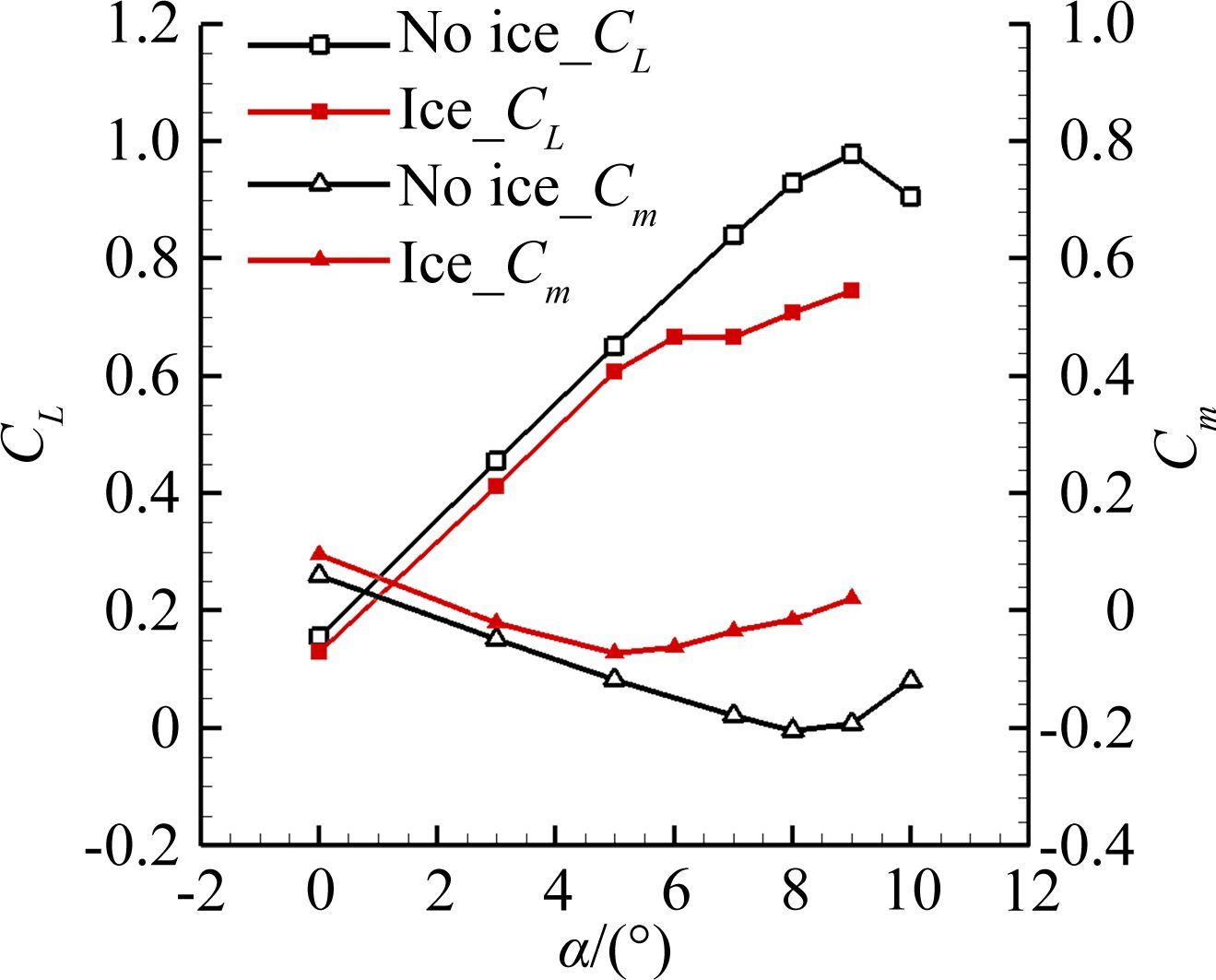
| 图 17 临界冰形对CRM升力和力矩系数影响 Fig. 17 Effect of critical ice shape on lift and moment |
|
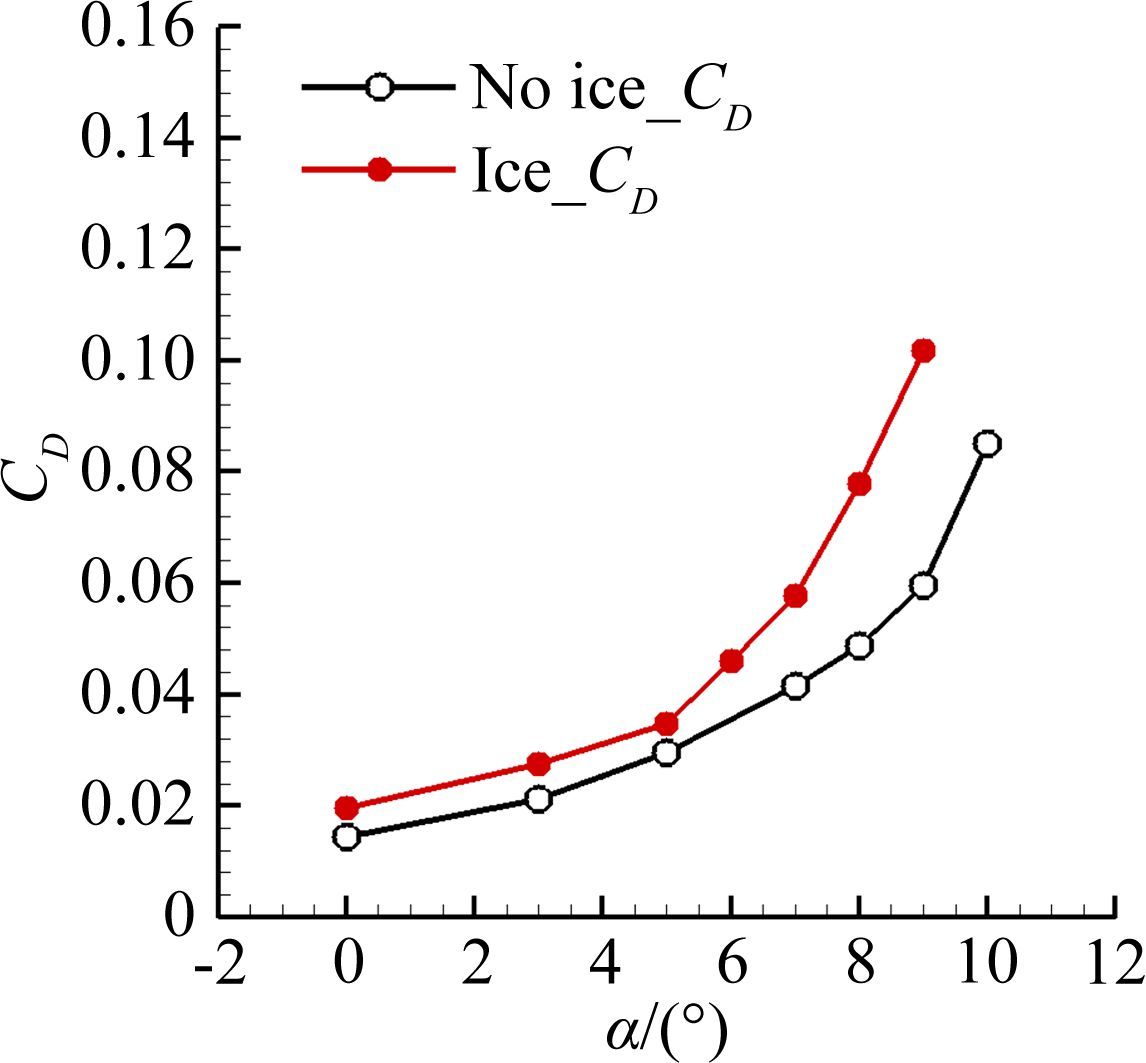
| 图 18 临界冰形对CRM阻力系数影响 Fig. 18 Effect of critical ice shape on drag |
从升力系数曲线中可以看出,结冰导致飞机升力特性衰减,升力系数衰减百分比为6.7%~23.8%,并且结冰导致飞机从升力线性段提前向非线性段发展,同时结冰后失速迎角减小了3°左右。结冰导致飞机俯仰力矩特性变化,结冰后增加飞机抬头力矩,但是在升力线性段纵向稳定性不变。随着迎角增加,结冰导致飞机提前发展至纵向不稳定状态。结冰会引起飞机阻力剧烈增加,最大增加70.9%左右,这必然造成飞机飞行过程中发动机推力变化,影响飞机航程等性能。结冰后飞机升阻比减小,结冰前Kmax约为22,结冰后下降到17.5。升阻比特性的下降,会导致飞机航程、续航时间、下滑距离和升限等性能的衰减。
| CL | CD | 升阻比Kmax | |
| 干净构型 | — | — | 22 |
| 带冰构型 | 减小6.7%~23.8% | 增加17%~70.9% | 17.5 |
5 结 论
本文分析了适航规章中对临界冰形的要求,发展了临界冰形确定的一般方法。并选取CRM飞机,以45min待机临界冰形为例,进行了临界冰形及其对飞机气动性能影响计算。研究得出以下结论:
1) 临界冰形分析是飞机适航取证中的重要工作,应该综合考虑不同飞行阶段、不同表面防护状态、防除冰系统工作形式等。通常要通过CFD、冰风洞试验、甚至是自然结冰试飞等手段综合确定。
2) FAR 25部附录C最大连续结冰条件下的45min待机冰形是必须要考虑的临界冰形之一。
3) 临界冰形的确定过程中,可以利用几何外形敏感性分析方法,即通过对比冰形的上下冰角角度和冰角厚度等冰形几何参数来确定最严重冰形。
4) 临界冰形的确定过程中,需要针对影响飞机结冰的温度、水滴直径、飞行条件等各类参数进行结冰敏感性分析,获得最严重结冰条件。
5) 临界冰形对飞机气动性能影响严重,导致升力降低6.7%~23.8%,阻力增加17%~70.9%,使飞机航程、续航时间、下滑距离和升限等性能衰减。
本文发展的45min待机临界冰形确定方法,能够利用数值模拟手段分析得到飞机的临界结冰条件和临界冰形,对于民用飞机设计和适航取证具有一定的工程应用价值。
| [1] | CCAR-25-R4. 中国民用航空规章第25部运输类飞机适航标准[S]. 中国民用航空总局,2011. |
| [2] | FAR Part 25. Airworthiness standards: Transport category airplanes[S]. U.S. Darpartment of Transportaton, 2011. |
| [3] | FAA. Advisory circular: certification of transport category airplanes for flight in icing conditions[Z]. 25.1419-1A, 2004. |
| [4] | DOT/FAA/AR. Report of the 12A working group on determination of critical ice shapes for the certification of aircraft[R]. DOT/FAA/AR-00/37, 2000. |
| [5] | FAA. Advisory circular: aircraft ice protection[Z]. 20-73A, 2006. |
| [6] | Yoeman K. Selection of the critical icing/flight case for an unprotected airfoil[R]. AIAA 1989-0757, 1989. |
| [7] | Parkins D C. Developing critical ice shapes for use in aircraft development and certification[R]. AIAA 2007-91, 2007. |
| [8] |
Chang S S, Yang Q M, Li Y. Quasi-steady numerical simulation of ice accretion on airfoil[J].
Acta Aerodynamica Sinica, 2011, 29(3):302–308.
(in Chinese) 常士楠, 杨秋明, 李延. 翼型表面结冰准定常数值模拟[J]. 空气动力学学报, 2011, 29(3) : 302–308. |
| [9] |
Yi X, Gui Y W, Zhu G L, et al. Experimental and computational investigation into ice accretion on airfoil of a transport aircraft[J].
Journal of Aerospace Power, 2011, 26(4):808–813.
(in Chinese) 易贤, 桂业伟, 朱国林, 等. 运输机翼型结冰的计算和实验[J]. 航空动力学报, 2011, 26(4) : 808–813. |
| [10] | 冯丽娟. 民用飞机结冰适航取证严重结冰条件的确定方法[J]. 中国科技信息, 2014(15) : 170–172. |
| [11] | Miller D R, Potapczuk M G, Langhals T J. Preliminary investigation of ice shape sensitivity to parameter variations[R]. AIAA 2005-0073. |
| [12] | Bourgault Y, Habashi W G, Dompierre J, et al. An eulerian approach to supercooled droplets impingment calculations[R]. AIAA 97-0176, 1997. |
| [13] | Ran P T, Brahim M T I, Paraschivoiu I. Ice accretion on aircraft wings with thermodynamics effects[J]. Journal of Aircraft, 1995, 32(2):444–446. DOI:10.2514/3.46737 |
| [14] | Papadakis M, Hung K E, Vu G T, et al. Experimental investigation of water droplet impingement on airfoils, finite wings, and an S-duct engine inlet[R]. NASA TM 2002-211700. |
| [15] | Shin J, Bond T H. Results of an icing test on a NACA0012 airfoil in the NASA Lewis Icing Research Tunnel[C]//30th Aerospace Sciences Meeting and Exhibit, 1992. |
| [16] | Wiberg B D, Fujiwara G E, Woodard B, et al. Large-sacale swept-wing icing simulations in the NASA Glenn Icing Research Tunnel using LEWICE3D[C]//AIAA Atmospheric and Space Environments Conference. 2014:95-96. AIAA 2014-2617. |


