2. 四川大学 工程力学系, 四川 成都 610065
2. Department of Engineering Mechanics, Sichuan University, Chengdu 610065, China
飞机结冰广泛存在于飞行实践中,是导致飞行安全事故的重要隐患[1-2]。结冰风洞试验是进行结冰研究的主要手段,它是通过在风洞内制造结冰气象条件,对真实结冰现象进行模拟[3]。为了使结冰风洞的试验结果与真实结冰一致,理想的方法是采用全尺寸的部件或者模型在对应的结冰气象条件下进行试验。但客观条件限制了这种理想方法的实现:一方面,风洞部件的尺寸往往太大,而风洞试验段的尺寸相对较小,不能满足进行全尺寸试验的要求;另一方面,实际的飞行条件和结冰气象参数范围很宽,由于制造工艺和设备模拟能力的限制,在结冰风洞内要完全达到这些条件是不可能的。因此,为了模拟真实结冰条件,结冰风洞的试验条件往往都是通过相似理论变换得到[4-5]。在进行相似变换时,有些参数的相似性要求不能完全满足,必须对由此带来的试验结果差异进行修正,Weber数差异即是其中的典型代表。Weber数定义为水滴惯性力与表面张力之比,从物理机理可知这个量主要影响结冰过程中水滴运动的形态、轨迹以及液态水在物体表面的溢流行为,这几方面的影响最终都可能使结冰形貌发生改变[6]。在进行结冰风洞试验时,让试验的Weber数与真实结冰的Weber数相等,已经成为确定试验条件的重要原则,为越来越多的研究者所建议和采用[7-8]。由于结冰风洞能达到的试验速度有限,如果试验模型有缩比,大部分结冰试验的Weber数不能与真实结冰条件的Weber数一致,而在FAA的Adviser Circular中有明确规定[9],如果试验的Weber数不能与真实结冰条件的Weber数相同,必须对相应的试验结果进行修正,这样获得的冰形才能用于飞机的适航认证。
国内外对于涉及结冰试验方案制订、试验参数选取以及试验输入数据相关性的结冰试验相似准则开展了较深入研究[10-13],有较多文章公开发表,但是对于结冰风洞试验数据的处理和修正,目前尚未见公开发表的研究报道。与常规风洞试验直接输出气动数据不同,大多数结冰风洞试验需要得到物体表面的结冰外形,对试验数据的修正即是对复杂冰形进行修正。
本文首先从理论上分析了进行冰形的Weber数修正的原因,在此基础上提出了一种根据几何特征量进行结冰外形修正的方法,并以某超临界翼型为对象,对不同Weber数条件下的结冰外形进行了仿真,研究了Weber数变化对结冰的影响规律,开展了基于等Weber数的结冰外形修正。
1 等Weber数的结冰试验参数选取方法 1.1 AEDC的结冰试验相似准则选取结冰试验参数的理论依据是结冰试验相似准则及相应的相似参数,相似参数的定义来自于影响结冰的各物理过程。根据影响结冰的主要因素,通常建立结冰试验相似准则时必须考虑如下4个方面:(1) 绕流流场;(2) 水滴运动轨迹和撞击特性;(3) 物面撞击水质量;(4) 结冰过程的热力学特性。
目前广泛应用的AEDC的结冰试验相似准则包涵了4个相似参数,分别为惯性因子K0、聚集因子Ac、冻结比例n和水滴能量传递势φ[10]。其中惯性因子K0是通过对水滴运动方程进行无量纲化而获得,其表达式为:
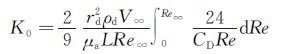
|
(1) |
式(1)中,rd、ρd和CD分别为水滴半径、密度和阻力系数,V∞为远场来流速度,μa为空气粘性系数,L为特征长度,Re∞为水滴在自由流中的雷诺数。

|
(2) |
聚集因子Ac的表达式为:
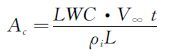
|
(3) |
其中,LWC为空气中的液态水含量,t为结冰时间,ρi为空气密度。
冻结比例n是指物面控制单元内所收集的液态水冻结成冰的比例。根据Messinger的结冰热力学模型可以得到冻结比例的表达式为[11]:
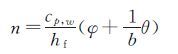
|
(4) |
其中,cp,w为水的比热,hf为冰的融解潜热,b为相对热因子,θ和φ分别为空气和水滴的能量传递势,具有温度量纲,φ的表达式为:

|
(5) |
AEDC的相似准则要求满足以下条件:
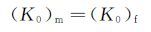
|
(6) |
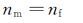
|
(7) |
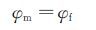
|
(8) |
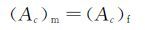
|
(9) |
其中下标“m”和“f”分别代表模型结冰的试验条件和全尺寸物体的参考结冰条件。
1.2 根据相似准则和参考条件确定试验条件确定了待模拟的参考结冰条件,根据相似准则的要求,即可根据参考条件选取对应的试验条件。需要选取的结冰试验参数共有7个,包括模型尺寸Lm、速度Vm、压力pm、水滴直径dm、液态水含量LWCm、结冰时间tm和温度Tm。而相似准则共有4个约束方程,因此在选取试验参数时可以自由指定3个。通常根据结冰风洞试验段大小指定试验模型尺寸,再自由给定速度和压力,其余试验参数则通过计算获得。根据式(6)~式(9)确定试验参数的公式为[10]:

|
(10) |
根据式(10)确定试验参数,需给定试验速度,再根据给定的试验速度计算其他参数,这导致试验速度给的不同,其他试验参数也不一样,对应试验冰形与参考冰形的相似程度也不一样,因次必须有给定试验速度的原则。文献[7]提出将等Weber数作为给定试验速度的原则,即:
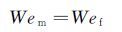
|
(11) |
根据Weber数的定义,有:
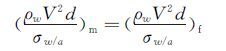
|
(12) |
其中σw/a为表面张力系数,由式(12)可得:
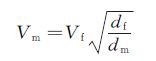
|
(13) |
需要注意的是,当按照等Weber数选取试验速度时,压力将不能自由给定。采用式(13)给出的试验速度之后,根据式(10),此时将有一个唯一对应的压力值。
由于试验模型缩比之后,试验的水滴直径dm要比参考水滴直径df小,导致按照式(13)计算的试验速度Vm大于参考速度Vf,这往往会超出结冰风洞的能力范围。如果试验速度达不到等Weber数的要求,有必要分析试验Weber数与要求Weber数不同所导致的试验结果差异,并对试验结果进行修正。
2 结冰外形修正方法 2.1 冰形相对误差的量化冰形修正的过程实质上是一个优化设计的过程,首先必须有一个基本的目标函数,取为修正后的冰形与目标冰形的相对误差,在此基础上才能建立冰形修正方法,使得修正后的冰形与目标冰形吻合得更好。因此,冰形修正的首要工作是建立冰形相对误差的定量计算方法。本文采用平均冰形几何特征量对比的方法对两组冰形的相对误差进行量化。
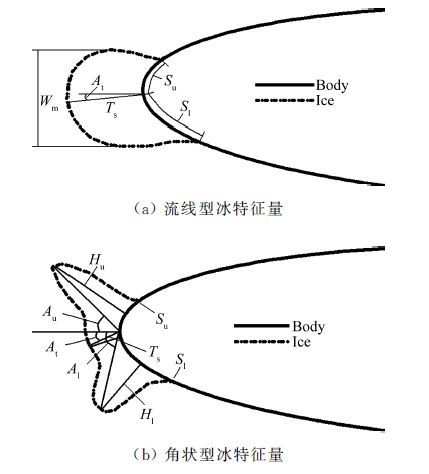
冰的外形轮廓可以分为流线型和角状型两大基本类型[12]。如图 1所示,流线型冰相对比较简单,采用驻点厚度Ts、驻点偏转角At、冰最大宽度Wm、结冰上极限Su和结冰下极限Sl等五个特征量就能基本描述其宏观轮廓,而角状冰相对复杂,需由八个特征量来描述,包括驻点冰厚度Ts、驻点偏转角At、上/下冰角的厚度(Hu和Hl)、上/下冰角的角度(Au和Al)、结冰上极限Su和结冰下极限Sl。
|
| 图 1 冰形特征量 Fig. 1 Geometric characteristics of ice |
冰形修正时,只需针对冰形的基本几何特征量进行修正,根据修正后的特征量得到相关特征点的修正值,进而采用TFI方法[14]得到修正后的整个冰形。
2.2 冰形几何特征量的修正模型冰形及其特征量受基体几何尺寸、液态水含量、水滴粒径、来流速度、温度、结冰时间等多个参数的共同影响,需要通过对各参数的影响程度进行准确地分析,才能建立合理可靠的修正模型。在结冰这一复杂过程中,冰形特征量与控制参数之间关系的系统方程过于复杂,各参数的灵敏度指标(一般取为一阶灵敏度系数,即系统输出对系统参数的一阶导数)无法直接计算得到,人工神经网络技术[15-16]在复杂非线性关系的模拟方面具有独到的优势,可用于冰形特征量的修正。
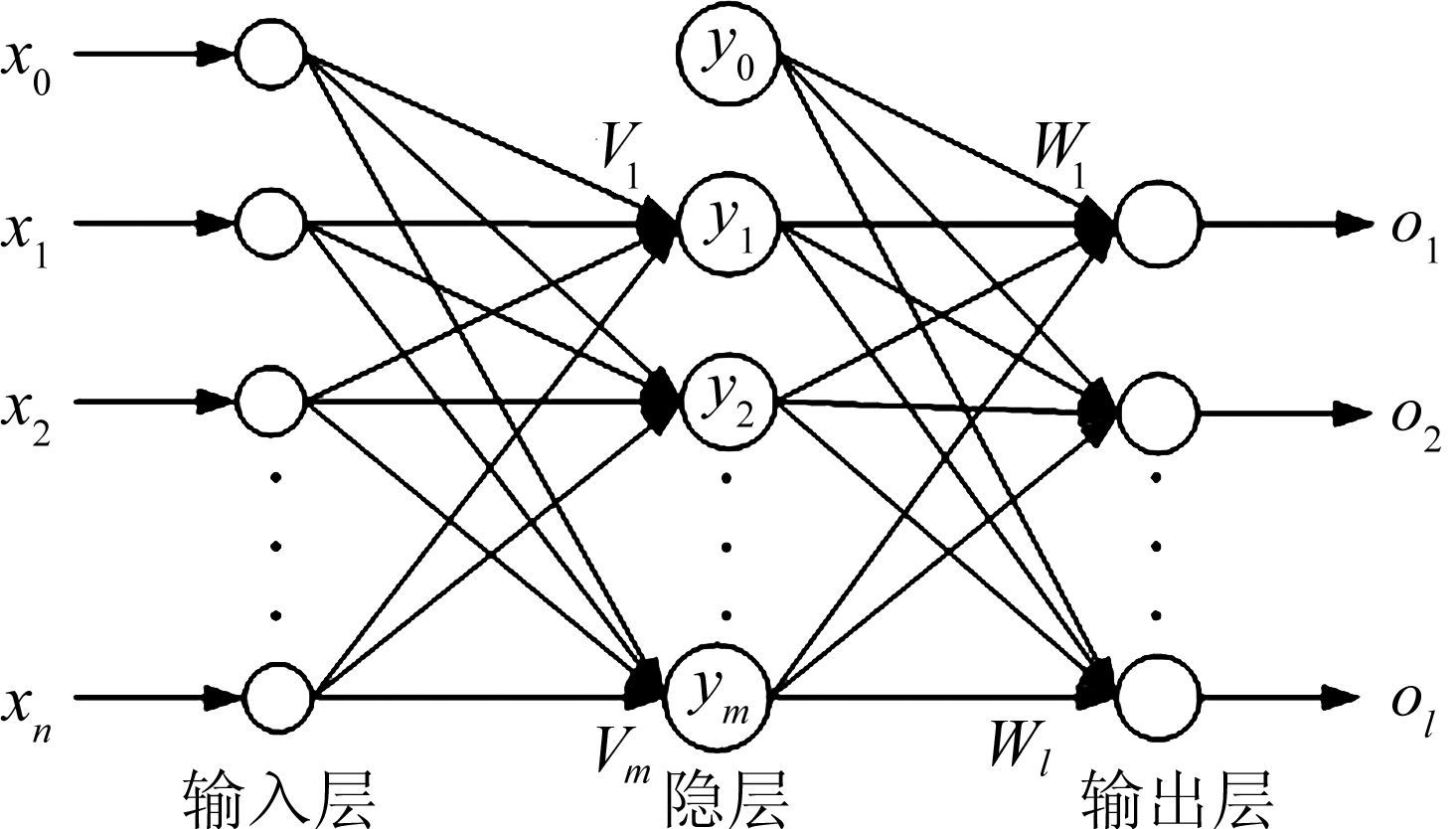
图 2为冰形与云雾参数之间的神经网络拓扑结构图,其中
输入向量:X=(x0,x1,x2,…,xn)T
隐层输出向量:Y=(y0,y1,y2,…,ym)T
输出层输出向量:O=(o1,o2,…,ol)T
期望输出向量: d=(d1,d2,…,dl)T
x0,x1,x2…,xn分别代表液态水含量、水滴粒径等输入参数;o0,o1…,ol分别代表采用人工神经网络方法预测的冰形特征量;d1,d2,…,dl分别代表冰形期望特征量,也即是数值预测或冰风洞试验得到的冰形特征量。
V=(V1,V2,…,Vm)、W=(W1,W2,…,Wl)分别为输入层到隐层、隐层到输出层之间的权值矩阵。
隐层和输出层的激活函数取为:
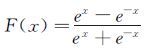
|
(14) |
|
| 图 2 三层BP模型 Fig. 2 Three-layer BP model |
冰形特征量的修正值计算公式如下:
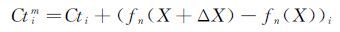
|
(15) |
其中,i=1,2,…,8分别代表八个不同的特征量,Ctim为第i个特征量修正值,Cti为试验值,fn为采用人工神经网络方法得到的冰形特征量,fn(X+ΔX)-fn(X)为冰 形系统模型在X附近的敏感度指标。由于冰形系统模型过于复杂,当同时存在多个输入变量需要修正时,采用针对单个变量进行分步修正的方法,每一步中对某一特定系统参数进行微小摄动,同时固定其它参数取值,进行相应的修正处理。
3 Weber数变化对结冰的影响研究针对某超临界翼型在典型Weber数条件的结冰结果进行了数值模拟,结冰计算方法参见文献[10]。在保持惯性因子、聚集因子、冻结比例和水滴能量传递势为常数的前提下,考察了Weber数变化对结冰外形的影响规律,并在此基础上针对Weber数偏差导致的结冰外形偏差进行了修正。
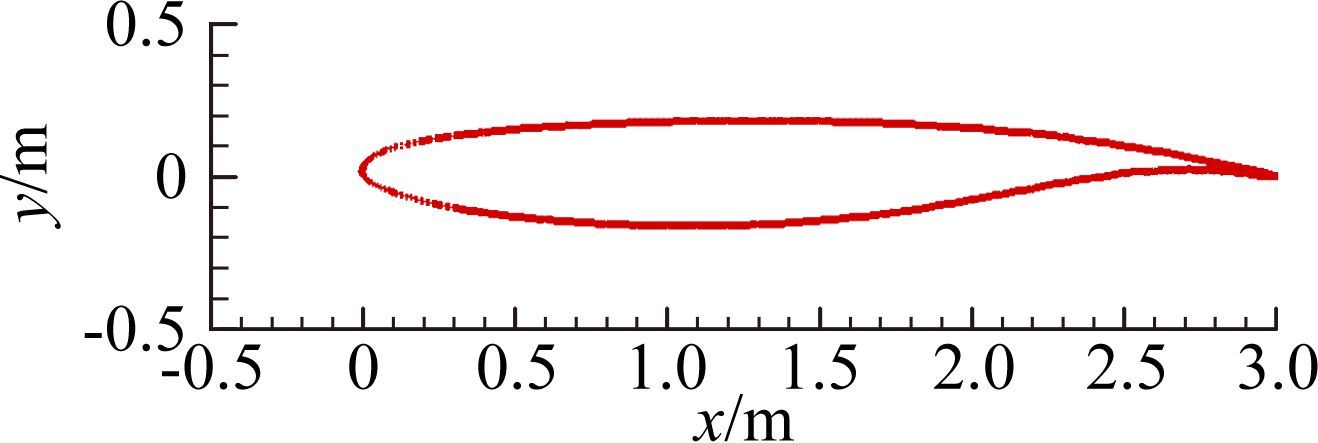
3.1 典型Weber数条件下的超临界翼型结冰计算研究所采用的超临界翼型源自某型运输机机翼剖面,如 图 3所示。翼型弦长3m,最大厚度0.35m,结冰计算条件为:特征尺寸3m,迎角0°,速度90m/s,压 强84606Pa,温度-8.8℃,水滴直径20μm,液态水含量0.5g/m3,结冰时间30min,由该条件计算的Weber数为2.49×103。
|
| 图 3 计算采用的超临界翼型 Fig. 3 Supercritical airfoil for simulation |
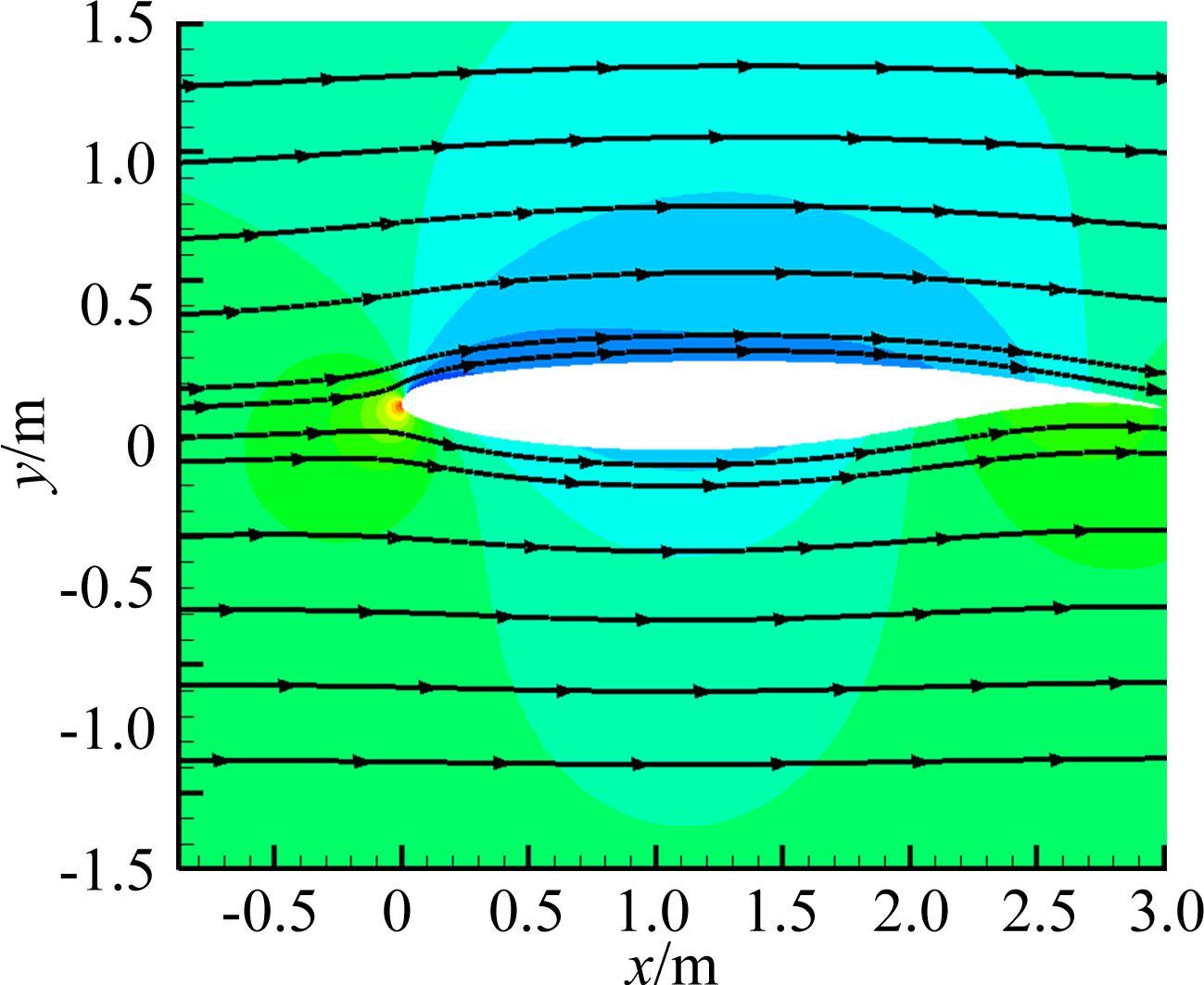
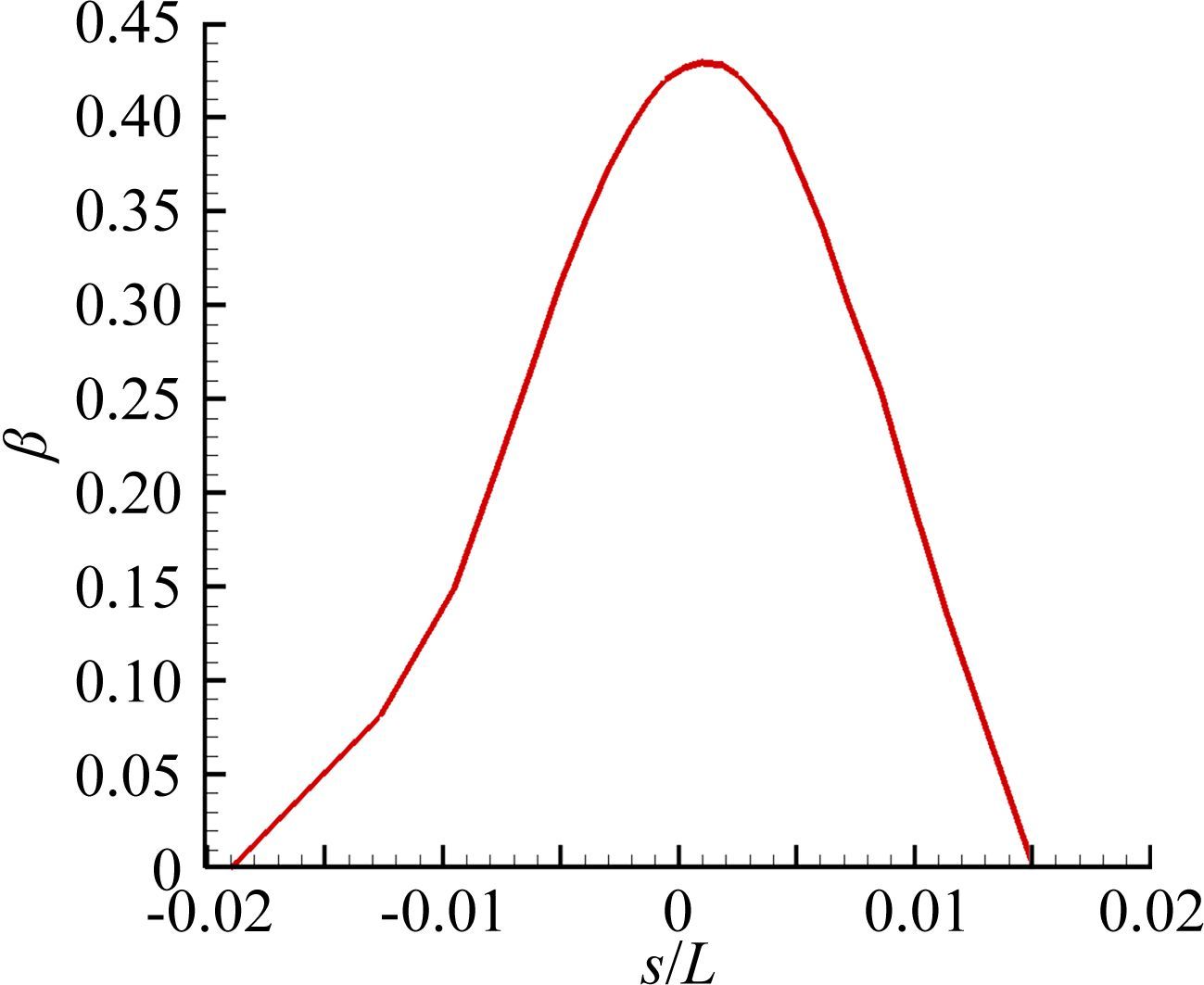
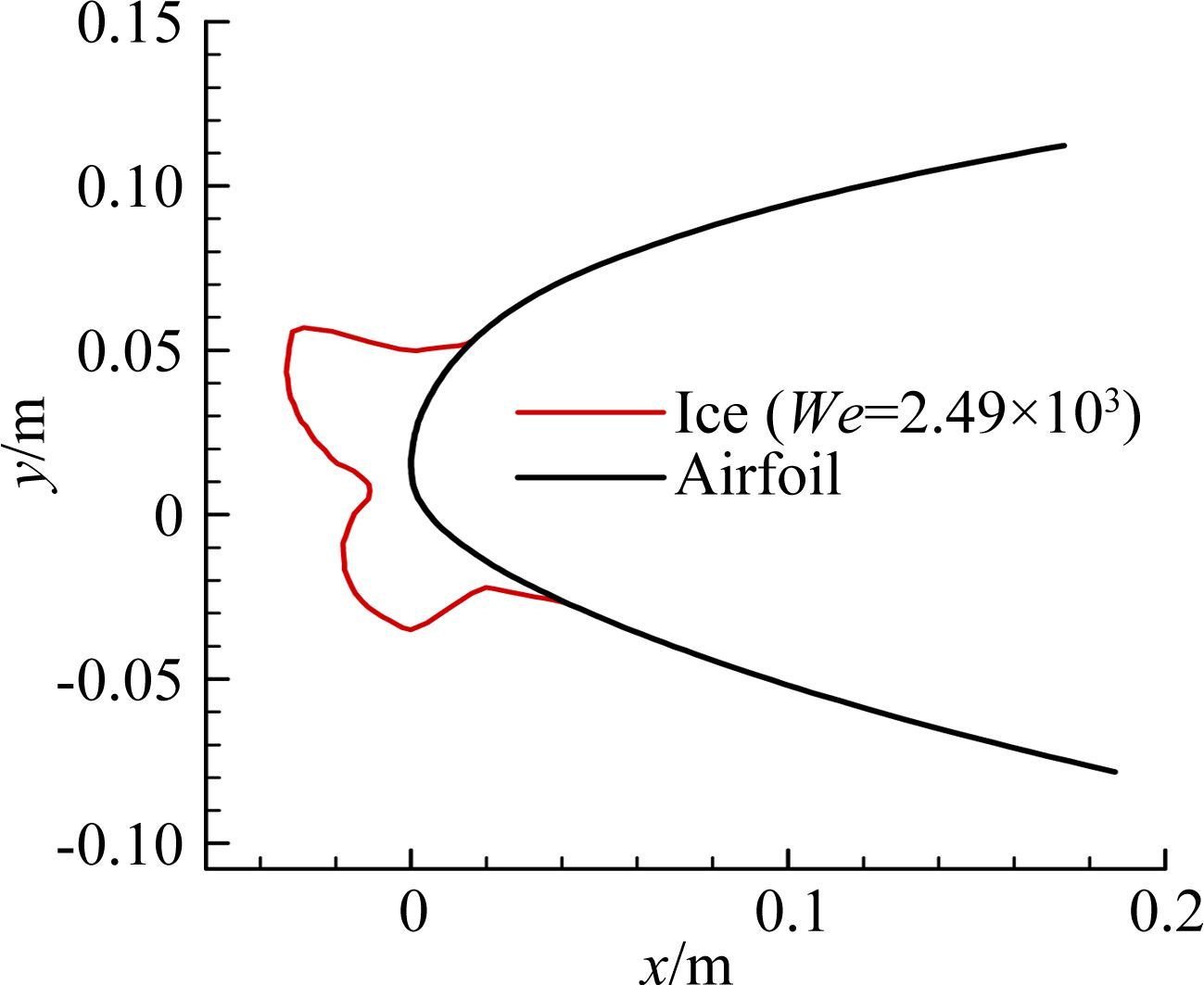
图 4给出的是绕翼型的流场分布,图 5给出的是水滴收集率曲线,水滴收集率的最大值为0.43,其位置在翼型前缘点偏上,这是由翼型的外形及流场分布所决定。图 6显示的是结冰外形,可以发现,冰体呈角冰形状,是典型的明冰,驻点冰厚较小,只有1.2cm,下冰角长度4.5cm,上冰角比下冰角更突出,厚度为5.7cm。
|
| 图 4 绕翼型的流场分布 Fig. 4 Distribution of flowfield about the airfoil |
|
| 图 5 水滴收集率曲线(We=2.49×103) Fig. 5 Curve of water droplet collection efficiency (We=2.49×103) |
|
| 图 6 翼型表面结冰外形(We=2.49×103) Fig. 6 Ice shape on the airfoil (We=2.49×103) |
3.2 Weber数变化对结冰的影响
为了考察Weber数变化对结冰外形的影响规律,以We=2.49×103典型算例的结果为标准,保持惯性因子、聚集因子、冻结比例和水滴能量传递势为常数,分别增加和减少Weber数,进行结冰外形进行了计算。
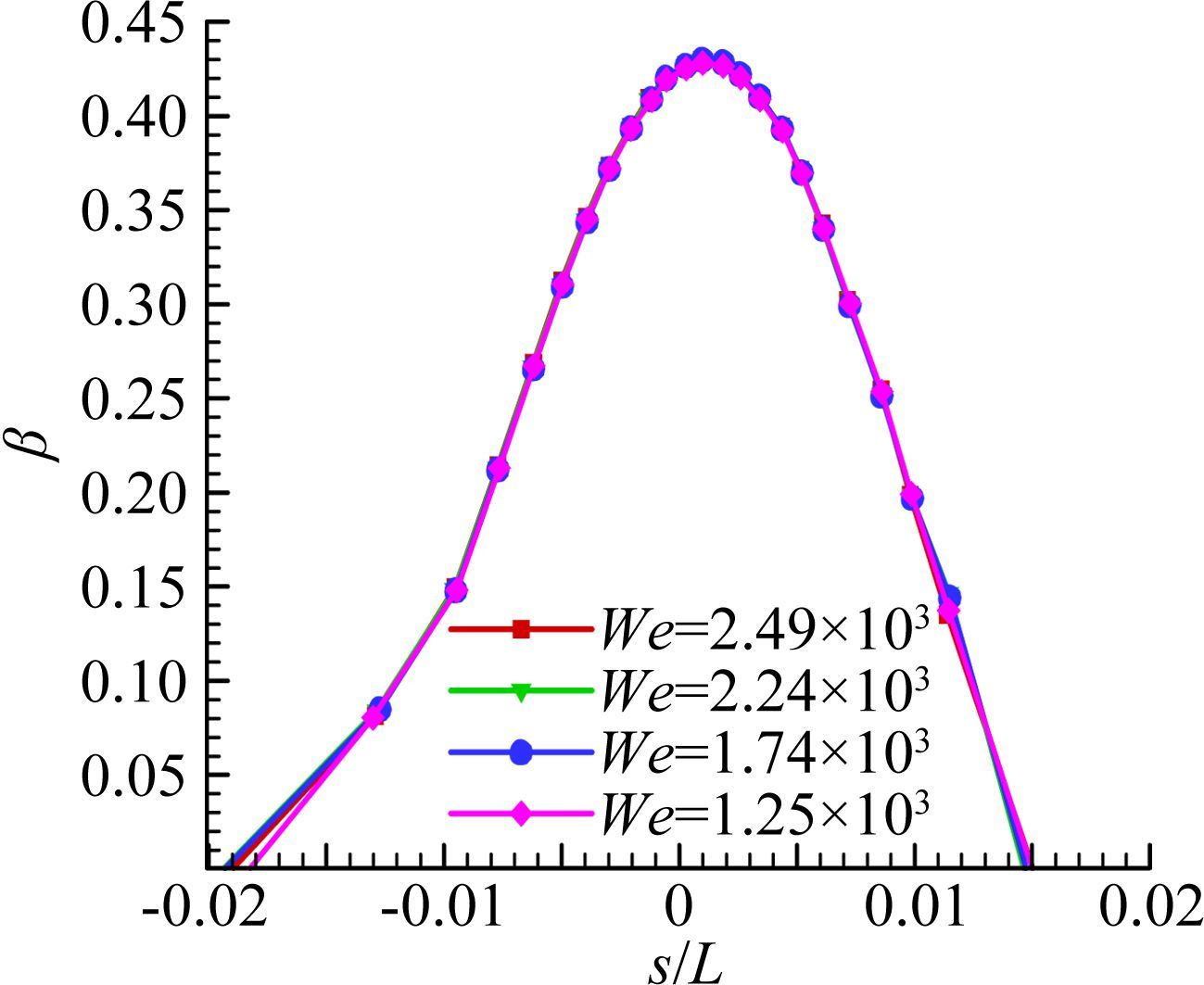
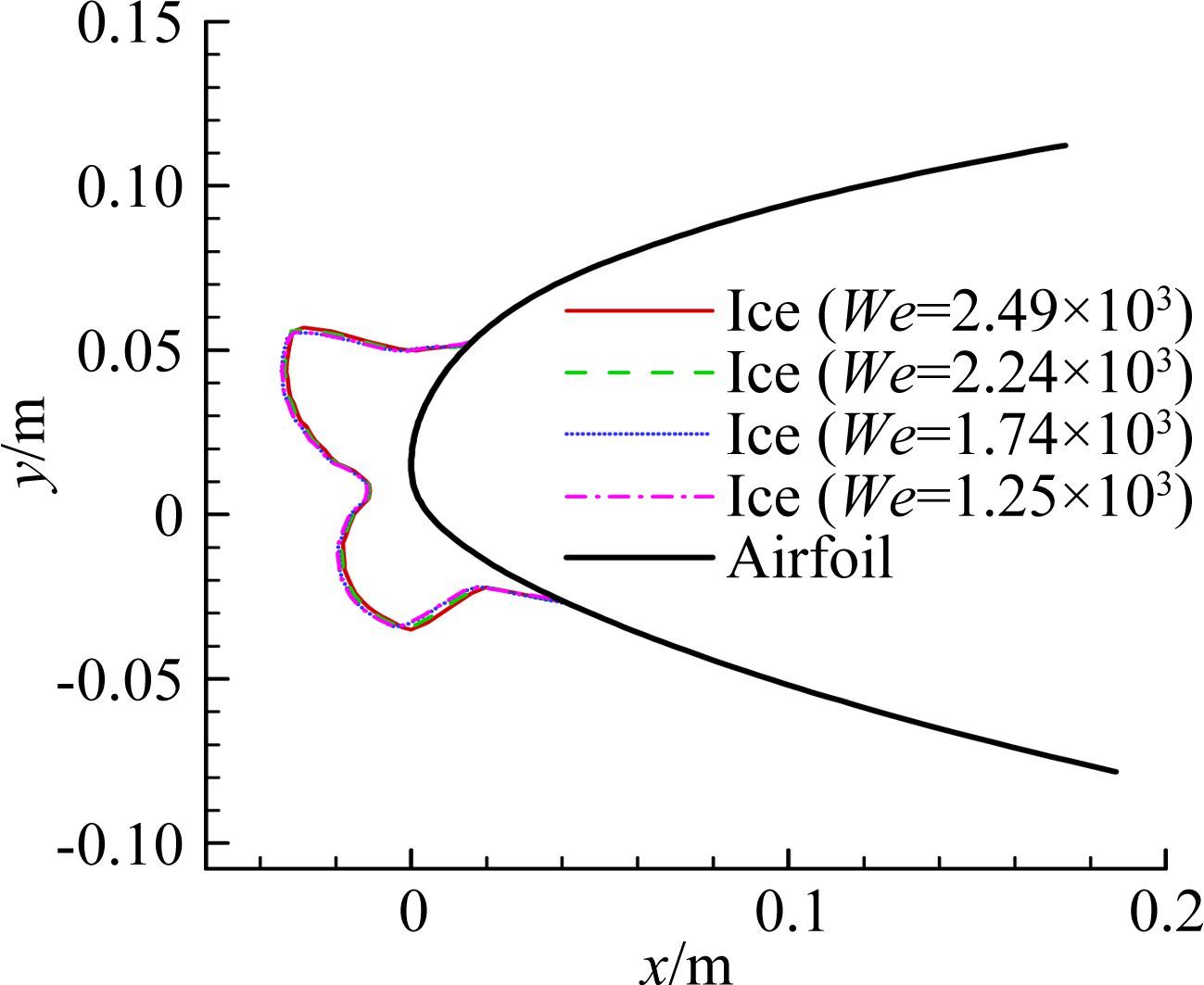
图 7给出的是在We=2.49×103的基准上,Weber数 分别减少10%(We=2.24×103)、30%(We=1.74×103)和50%(We=1.25×103)之后的水滴收集率分布曲线。图 8给出的是结冰外形。对比表明,不同Weber数条件下的水滴收集率和结冰外形均保持一致,说明在计算的Weber数范围内,只要惯性因子、聚集因子、冻结比例和水滴能量传递势保持不变,Weber数减小至基准Weber数50%以内,水滴收集率和结冰外形均不受影响。
|
| 图 7 水滴收集率对比(减小Weber数) Fig. 7 Comparison of water droplet collection efficiency (decreasing Weber number) |
|
| 图 8 结冰外形对比(减小Weber数) Fig. 8 Comparison of ice shape (decreasing Weber number) |
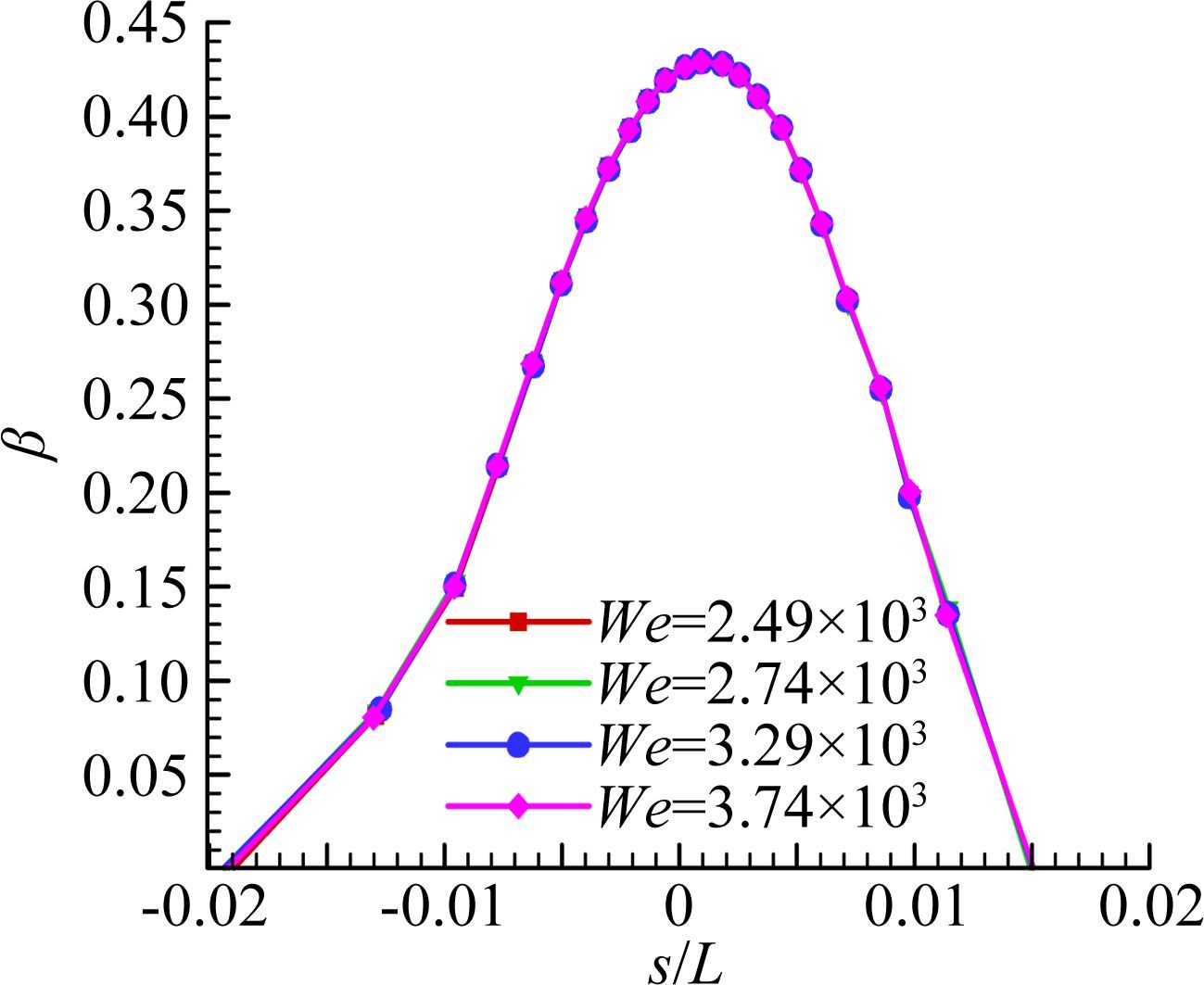
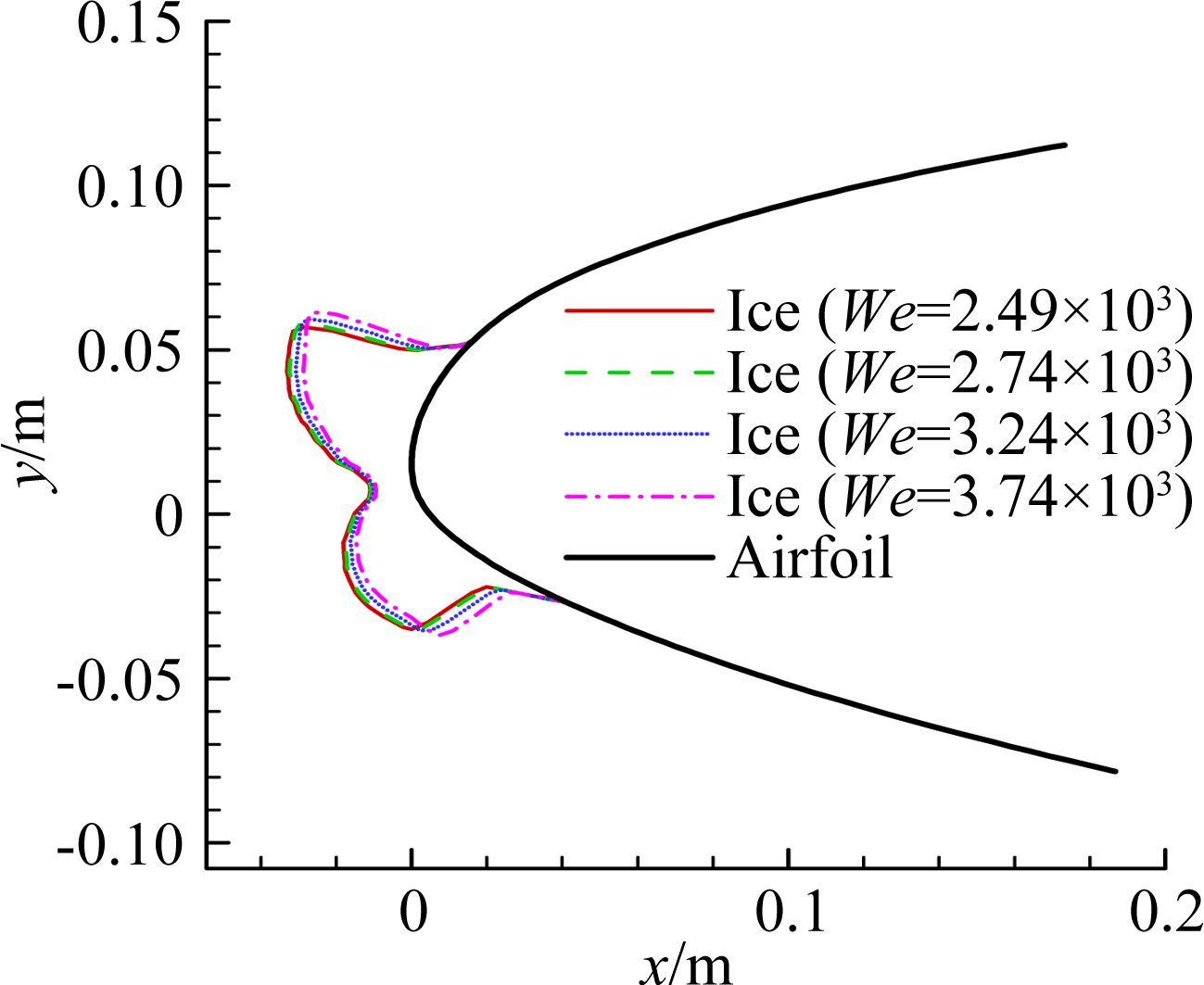
图 9给出的是在We=2.49×103的基准上,Weber数分别增 加10%(We=2.74×103)、30%(We=3.29×103)和50%(We=3.74×103)之后的水滴收集率分布曲线。计算表明不同Weber数条件下的水滴收集率保持一致,说明Weber数增加对水滴收集率无影响。图 10给出的是结冰外形对比,可以发现,随着Weber数增加,结冰外形有明显变化,具体变化趋势为:驻点冰厚保持不变,上冰角向后上方移动,下冰角向后下方移动,冰体的迎风面积增加,上下冰角之间的张角增加。Weber数增加10%时的冰形与基准冰形接近,Weber数增加大于30%之后的冰形与基准冰形有明显差异。
|
| 图 9 水滴收集率对比(增加Weber数) Fig. 9 Comparison of water droplet collection efficiency (increasing Weber number) |
|
| 图 10 结冰外形对比(增加Weber数) Fig. 10 Comparison of ice shape (increasing Weber number) |
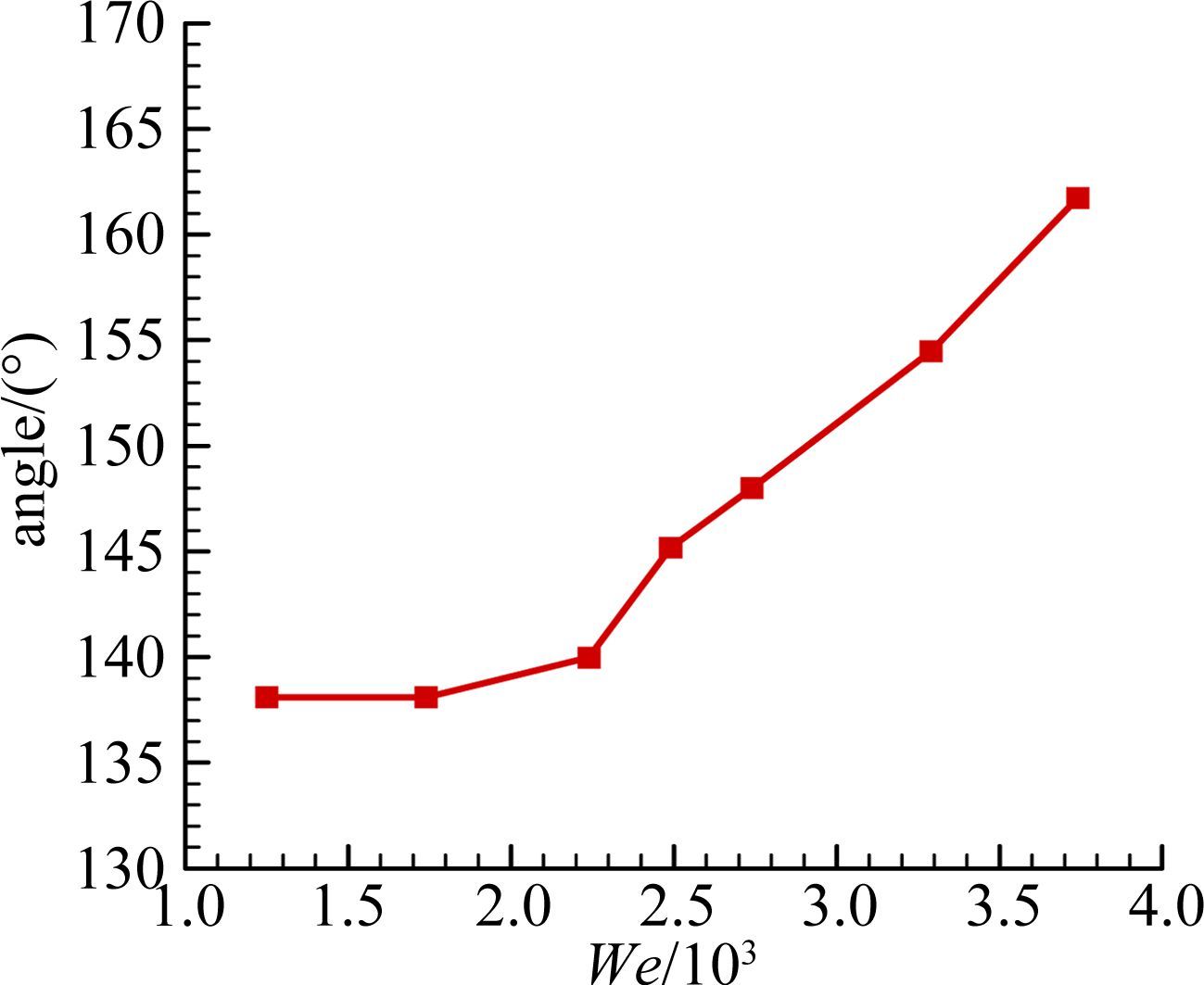
图 11给出的是上冰角与下冰角之间的张角随着Weber数变化而改变的曲线。可以看到,Weber数小于2.24×103时,Weber数变化对张角影响较小,Weber数从1.25×103增加至于2.24×103,张角仅增加2°。Weber数大于2.24×103之后,张角随着Weber数增加而增加的幅度明显加大,Weber数从2.24×103增加至于3.79×103,张角增加达21°。
|
| 图 11 不同Weber数条件下的冰角张角 Fig. 11 Angles between upper and lower ice horns for different Weber number |
对比分析 图 8、图 10和图 11可知,在惯性因子、聚集因子、冻结比例和水滴能量传递势保持不变的情况下,存在一个敏感Weber数。低于敏感值时,Weber数变 化对结冰影响不大,而Weber数高于敏感值时,Weber数变化对结冰有明显影响。对于文本的算例,Weber数的敏感值在2.24×103附近。
4 基于等Weber数的结冰外形修正从第3节的计算结果可以看出,在只有Weber数存在误差、其他相似量保持常数的前提下,冰形特征量的变化将主要体现为上下两个冰角特征的改变。因此,尽管角状冰有八个特征量,但若仅仅变化Weber数,只需要修正上下冰角长度及角度这四个量就能基本保证冰形修正的精度。n组Weber数和对应的冰形上下冰角长度及角度四个特征量可以构成四个三次样条函数,对应的坐标分别为:xi,n=Wen,yi,n=fi(Wen),i=1,…,4。冰形修正处理时,修正前后的Weber数分别为Weo和Wec,基于修正前Weber数得 到的冰形对应的各特征量分别为Ci(Weo),则可根据如下公式进行各特征量的修正:
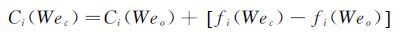
|
(16) |
修正后的冰形数据点坐标为:
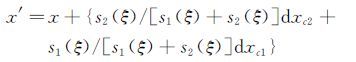
|
(17) |
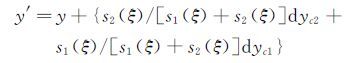
|
(18) |
s1(ξ),s2(ξ)分别为冰形对应左右特征点的距离。
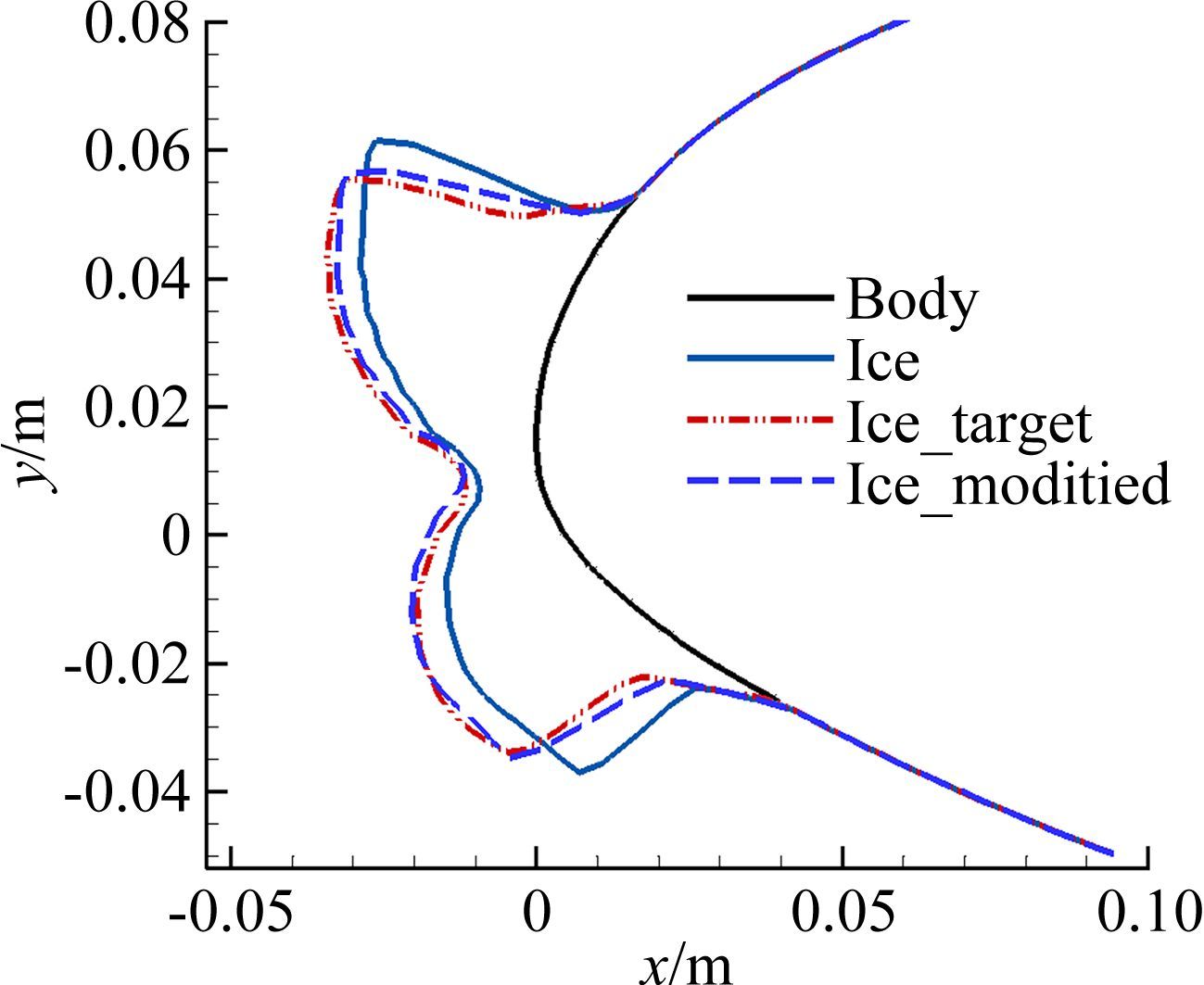
若试验需要模拟We=1.25×103条件下的冰形,实施过程中由于控制、测量或试验条件受限等原因使得真实试验条件为We=3.74×103,采用本文的修正方法对冰形进行修正,图 12给出了修正前后冰形与目标冰形的对比。从图 12中可看出,修正后的冰形上下冰角位置、驻点位置、整体轮廓等都明显比修正前的冰形与目标冰形的吻合度更好。
|
| 图 12 冰形修正结果(减少Weber数) Fig. 12 Ice modification result (decreasing Weber number) |
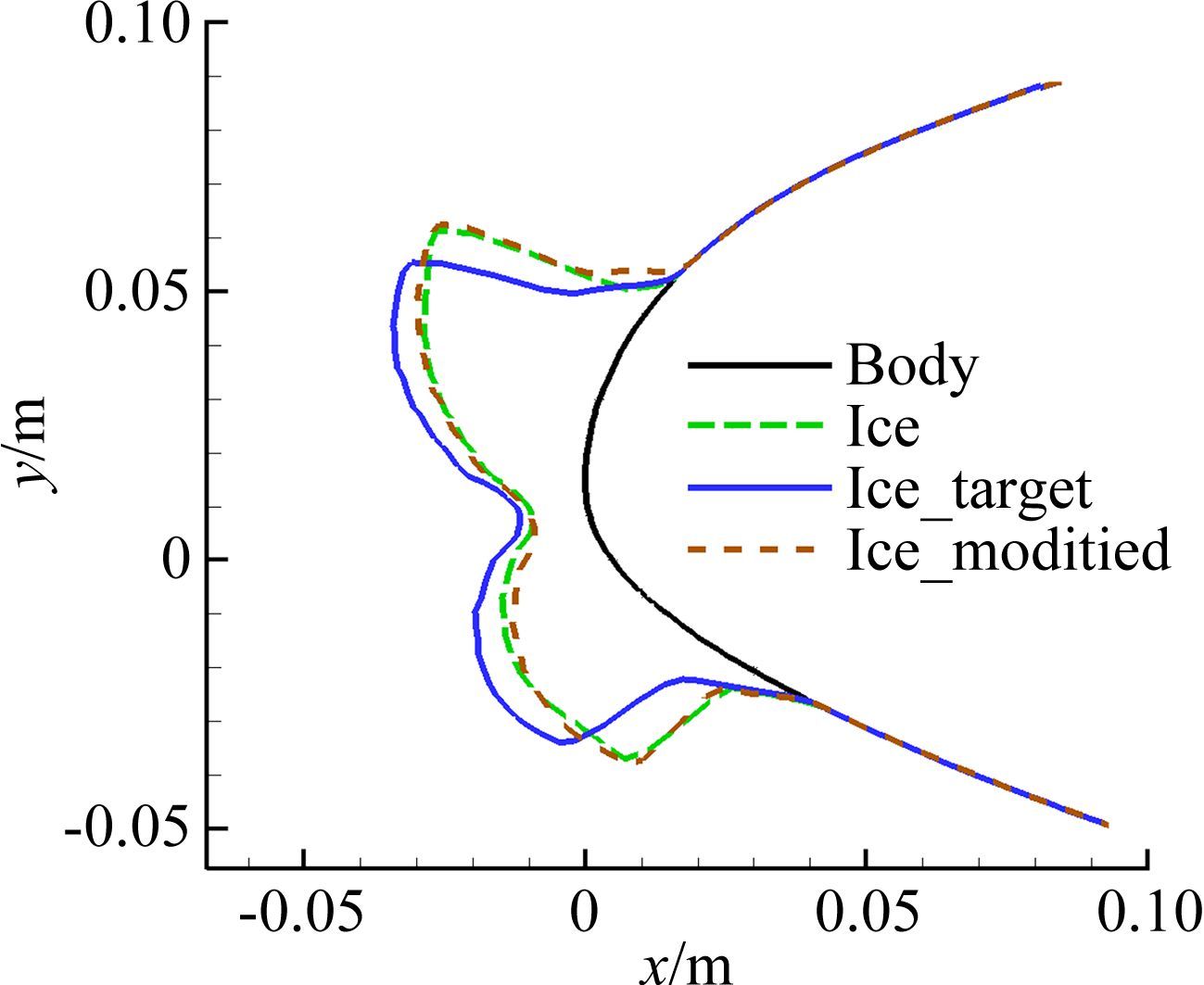
反之,若试验需要模拟We=3.74×103条件下的冰形,实施过程中由于控制、测量或试验条件受限等原因使得真实试验条件为We=1.25×103,采用本文的修正方法对冰形进行修正,图 13为修正前后冰形与目标冰形的对比。修正后的冰形也明显比修正前的冰形与目标冰形更吻合。
|
| 图 13 冰形修正结果(增加Weber数) Fig. 13 Ice modification result (increasing Weber number) |
5 结 论
根据几何特征量进行结冰外形修正的方法,对某超临界翼型的结冰情况进行了数值仿真,研究了Weber数变化对结冰的影响规律,开展了基于等Weber数的结冰外形修正,得到如下结论:
(1) 在惯性因子、聚集因子、冻结比例和水滴能量传递势保持不变的情况下,Weber数变化主要影响冰角特征,对水滴收集特性、驻点冰厚和结冰极限等影响较小;
(2) 存在一个敏感Weber数,低于敏感值时,Weber数变化对冰形影响不大,当Weber数高于敏感值时,Weber数变化对冰形将有明显影响;
(3) 根据几何特征量进行冰形修正的方法能保证冰形的宏观轮廓与目标冰形一致,修正后的冰形能适量消除由于Weber数误差导致的冰形差异,提高试验的精度。
Weber数对结冰的影响及相应的冰形修正,涉及到复杂空气流场中液态水在物面的撞击特性及动力学效应。本文工作是对该问题的初步探索,虽然结果让人满意,但还需进一步深入和完善,尤其需要开展大量的试验研究和验证工作。
| [1] | Cebeci T, Kafyeke F. Aircraft icing[J]. Annual Review of Fluid Mechanics, 2003, 35:11–21. DOI:10.1146/annurev.fluid.35.101101.161217 |
| [2] | Bragg M B, Broeren A P, Blumenthal L A. Iced-airfoil aerodynamics[J]. Progress in Aerospace Sciences, 2005, 41(5):323–362. DOI:10.1016/j.paerosci.2005.07.001 |
| [3] | Soeder R H, Sheldon D W, Robert F S, et al. NASA Glenn icing research tunnel user manual[R]. NASA TM 2003-212004, 2003. |
| [4] | Ruff G A. Verification and application of the icing scaling equations[R]. AIAA 86-0481, 1986. |
| [5] | Anderson D N. Methods for scaling icing test conditions[R]. AIAA 95-0540, 1995. |
| [6] | Anderson D N. Manual of scaling method[R]. NASA CR 2004-212875, 2004. |
| [7] | Bilanin A J. Proposed modifications to ice accretion/icing scaling theory[J]. Journal of Aircraft, 1991, 28(6):353–359. DOI:10.2514/3.46034 |
| [8] | Bilanin A J, Anderson D N. Ice accretion with varying surface tension[R]. AIAA 95-0538, 1995 |
| [9] | Susan J M. Aircraft ice protection[R]//FAA Advisory Circular, No. 20-73A, 2006. |
| [10] |
Yi X.Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang: China Aerodynamics Research and Development Center, 2007. (in Chinese). 易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳: 中国空气动力研究与发展中心, 2007. |
| [11] |
Yi X, Zhu G L, Gui Y W. Modification and evaluation of an icing scaling law[J].
Journal of Experimentals in Fluid Mechanics, 2008, 22(2):84–87.
(in Chinese) 易贤, 朱国林, 桂业伟. 一种改进的积冰试验相似准则及其评估[J]. 实验流体力学, 2008, 22(2) : 84–87. |
| [12] | Ruff G A. Quantitative comparison of ice accretion shapes on airfoils[J]. Journal of Aircraft, 2002, 39(3):418–426. DOI:10.2514/2.2967 |
| [13] | Anderson D N, Tsao J C. Ice shape scaling for aircraft in SLD conditions[R]. NASA CR 2008-215302, 2008. |
| [14] |
Zhou Z H, Li F W, Li G N. Applying Eulerian droplet impingement model to numerically simulating ice accretion but with some improvements[J].
Journal of Northwestern Polytechnical University, 2010, 28(1):138–142.
(in Chinese) 周志宏, 李凤蔚, 李广宁. 基于两相流欧拉方法的翼型结冰数值模拟[J]. 西北工业大学学报, 2010, 28(1) : 138–142. |
| [15] | Li H J. Neural network modeling and optimization of semi-solid extrusion for aluminum matrix composites[J][J]. Journal of Materials Processing Technology, 2004, 151(3):126–132. |
| [16] | Saltelli A. Sensitivity analysis[M]. Chichester: Wiley, 2000 . |



