高效减阻是飞机设计师和制造者的一个长期目标,通过减小飞行阻力可降低飞机运行成本,同时还能减少燃料污染物的排放,从而降低空中环境污染,这在科学技术高速发展的当今时代显得尤为重要[1]。飞机巡航阻力中,摩擦阻力是一个重要的组成部分, 对于亚声速飞机,表面摩擦阻力占总阻力的50%左右[2]。因此, 减小摩擦阻力成为当今飞机减阻设计的研究热点。表面摩擦阻力的减少主要包括延迟边界层转捩和减小湍流区摩擦阻力两方面。
在众多的减阻控制技术中,壁面温度控制方法出现的相对较晚,1986年,Lin[3]对一个近似于机身的细长对称钝体进行壁面加热数值研究,发现加热能够减小摩擦阻力,并使总阻力减小。1999年,Kramer[4]在Lin的基础上,对细长钝体的不同位置进行了加热控制的实验研究,发现加热位置越靠前,加热面积越大,减阻效果越好。Lin和Kramer认为阻力的变化是因为壁面温度影响了湍流边界层,但并没有指出是如何影响。李轶明[5]、张振[6]等通过对空气从平板下方流过时的湍流区进行壁面加热实验,发现板面附近的流动出现了从湍流流动转变为层流流动的逆转捩现象,导致壁面摩擦系数出现大幅下降。这与空气从上方流过平板的情况并不相同,而且他们都没有考虑壁面温度控制对层流流动和边界层转捩的影响。
相对于摩擦阻力的研究,壁面温度控制对层流稳定性和边界层转捩影响的研究就早得多。早在1947年,Lees[7]就发现壁面冷却能够稳定平板边界层中的二维扰动;1976年,Boehman[8]发现壁面冷却能够稳定跨声速流动中二维和三维扰动;1980年,Potter[9]对当时关于高超声速情况下壁面冷却的实验进行了总结,发现大部分情况下,壁面转捩雷诺数随着冷却程度的加剧而增大。之后,也陆续出现了这方面的研究,然而,这些研究主要集中在高超声速和跨声速领域,或者是仅关注边界层内某种扰动的发展[10-12]。因此,低速下,温度控制对边界层转捩的影响还有待进一步研究。
基于上述原因,本文在低速范围内,利用数值模拟方法,通过对零压力梯度的平板边界层流动施加温度控制,展开壁面温度控制对平板层流边界层和湍流边界层影响的研究,探索温度控制对平板转捩雷诺数和壁面摩擦阻力的影响规律。
1 数值计算方法 1.1 转捩模式转捩位置预测是研究边界层转捩需要解决的关键技术和难点,由于风洞实验周期长、费用高,使得数值方法逐渐成为转捩预报的主要手段。目前关于转捩预报的数值方法有很多,湍流转捩模式法是一种常用的转捩预测方法,其计算周期短,对计算机性能的要求较低,是十分有效的数值方法。本文数值计算的湍流模型采用带有转捩模式的三方程涡粘(Transition k-kl-ω)模型。该模型由Walters和Davor[13]两人提出,在k-ω方程的基础上,增加一个描述层动能的输运方程。模型输运方程为:
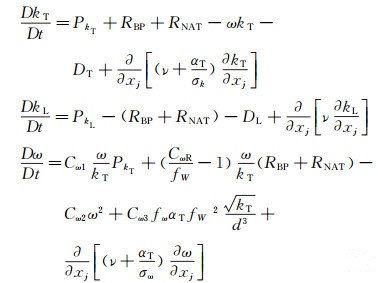
|
(1) |
式中: kT、kL和ω分别为湍动能、层动能和湍流时间尺度,P项、R项、D项、k项及最后的偏微分项分别为产生项、转捩产生项、破坏项、耗散项和梯度输运项。其中转捩产生项用来描述转捩发生过程中的湍流长度尺度的衰减。如果存在热传递效应,模型引入一个湍流热耗散系数对热流量方程进行修正。关于这一模型的更多介绍,可参考文献[13]。
1.2 物理模型与数值方法数值计算选用零压力梯度的平板,平板长2.5m,来流马赫数Ma=0.3,温度T=288K。
计算采用CFD商业软件,求解定常可压缩质量加权的NS方程、能量方程和Transition k-kl-ω转捩模型。使用双精度求解器,方程的离散采用有限体积法,对流项采用二阶迎风格式离散,扩散项采用中心差分格式离散,压力和速度耦合采用Simple算法。平板表面满足无滑移边界条件,入口和出口分别为质量入口和压力出口边界条件,平板上方采用对称边界条件。
计算域流向长2.5m,与平板重合,法向高1m。为了更好的模拟边界层流动,计算域流向共布置520个网格点,并对转捩区附近进行了局部网格加密;法向共布置150个网格点,第一层网格高度为1×10-6m,并满足y+在0.1~0.2之间;合计网格数约7.8×104。
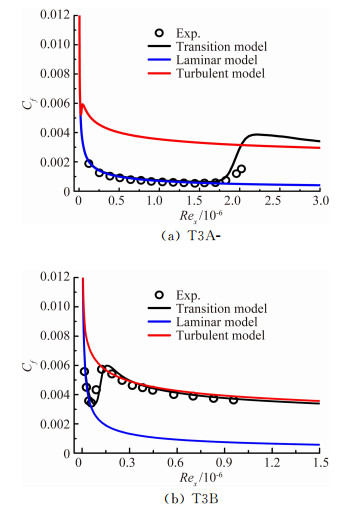
1.3 算例验证为了验证转捩模式和数值计算方法的预报精度,针对文献[14]给出的零压力梯度T3A-和T3B实验,进行数值计算对比验证分析,相关计算参数见表 1。图 1给出了基于这一转捩模式的转捩解和层流解、SST k-ω湍流解的计算结果,并与实验值进行对比。图中:Cf为表面摩擦系数,Rex为沿流向的当地雷诺数,定义见式(2),式中ρ、U、μ分别为自由来流的密度、速度和粘性系数,x为流向位置坐标。
|
| 图 1 平板表面摩擦系数分布的计算与实验值 Fig. 1 Distribution of skin friction coefficient for T3A-and T3B flat plates |
| Vase | Velocity/(m·s-1) | Turbulent intensity/% | Turbulentviscosity ratio | Pressure gradient |
| T3A-T3B | 19.89.4 | 0.8746.5 | 8.73100.0 | 00 |
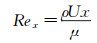
|
(2) |
图 1表明,这一转捩模式和计算预报精度良好,能够准确的模拟层流区、转捩区和湍流区的表面摩擦系数;并且采用的湍流模式能够准确的预测转捩位置。
2 计算结果分析为了衡量不同控制条件下,平板转捩雷诺数和摩擦阻力的相对变化规律,定义了无量纲的温度Tw*、转捩雷诺数ReT*和摩擦阻力Dw*,其表达式如下:

|
(3) |
式中: Tw、ReT和Dw分别为控制温度下平板的壁面温度、转捩雷诺数和摩擦阻力,Taw、ReaT和Daw分别为绝热壁面平板的温度、转捩雷诺数和摩擦阻力。
2.1 温度控制对壁面摩阻系数的影响图 2为不同控制温度下,平板壁面摩擦阻力系数的分布规律。由图可知,壁面加热会延迟边界层转捩,降低湍流区的摩阻系数;而壁面冷却会使转捩提前,并增大湍流区的摩阻系数。

|
| 图 2 平板表面摩擦系数分布 Fig. 2 Distribution of skin friction coefficient for flat plate |
2.2 温度控制对边界层转捩的的影响
层流流动经常会受到一些小的扰动,如果扰动随时间放大,则流动是不稳定的,层流会发生转捩转变为湍流。对于顺流放置的平板,随着流动发展,边界层雷诺数达到转捩临界雷诺数,转捩就会发生。壁面温度控制导致边界层内出现温度梯度,影响空气粘性系数和密度,进而对边界层转捩产生影响。图 3给出了平板转捩雷诺数在不同控制温度下的变化规律。由图可见,壁面加热会增大转捩雷诺数,延迟转捩。当控制温度从绝热壁面温度288K增大至432K时,转捩雷诺数增大约36%,控制效果良好。

|
| 图 3 平板转捩雷诺数变化规律 Fig. 3 Variation of transition Reynolds numbers for flat plate |
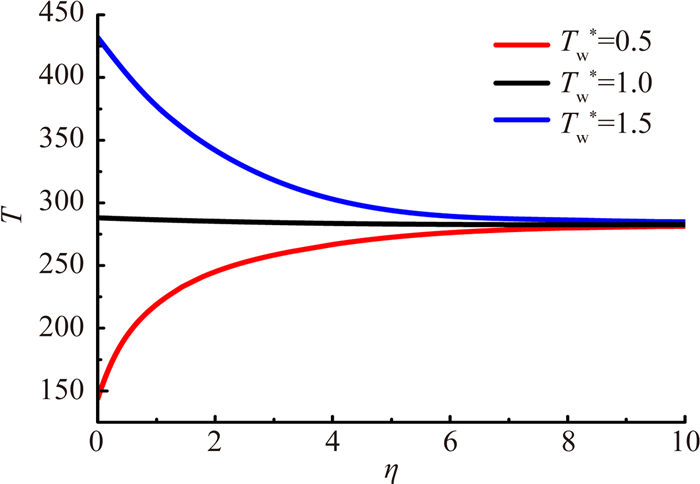
研究温度控制对层流边界层的影响,如图 4为在绝热壁面转捩起始位置,即当地雷诺数Rex=0.75×105处,边界层内空气温度的分布规律,图中η定义见式(4)。由图可见,加热使边界层内出现了近壁面温度高,远离壁面处温度低的温度梯度,这将进一步导致边界层内出现近壁面处空气粘性系数较大的粘性分层和密度较小的密度分层。
|
| 图 4 平板边界层内温度分布规律 Fig. 4 Variation of thermal boundary-layer |
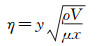
|
(4) |
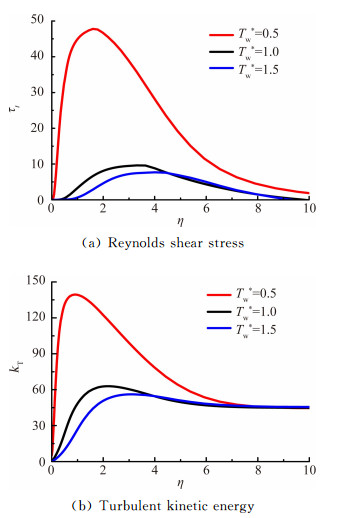
在湍流运动中,流体质点除主流方向的运动外,还存在沿不同方向的脉动,一般可使用雷诺切应力和湍动能代表脉动对时均流动的影响。图 5为在相同位置处,温度边界层内雷诺切应力τt和湍动能kT的分布规律。由图 5可知,壁面加热控制减小了边界层内雷诺切应力和湍动能,即壁面加热抑制了边界层内的切向脉动和正向脉动,稳定了边界层内流动。因此,壁面加热控制会延迟层流流动向湍流流动的转捩,增大转捩雷诺数,扩大层流区。
|
| 图 5 边界层内雷诺切应力和湍动能分布规律 Fig. 5 Variation of Reynolds shear stress and turbulent kinetic energy of boundary-layer |
根据雷诺切应力的定义, τt=-ρ〈u'v'〉,壁面加热控制使雷诺切应力减小是因为,加热会导致边界层内空气密度减小;而且,加热使空气粘性系数增大,粘性作用增强,近壁区速度减小,使得当地雷诺数变小,同时由于粘性作用增强,流体微团速度变化需要克服的粘性阻力更强,边界层内速度分布更加均匀,使得不同流层之间的动量交换与混掺变弱,进而导致脉动受到抑制。另一方面,壁面加热导致边界层内出现近壁区流体密度小,远离壁面区域流体密度大的密度分层。由于下方密度小,空气会向上方扩散,并克服重力做功,湍动能转化为重力势能,进而导致湍动能减小。
2.3 温度控制对湍流边界层的影响表面摩擦阻力的减小一直是空气动力学界最具有挑战性的研究领域之一。壁面加热控制延迟边界层转捩,扩大层流区,由于层流摩阻要远小于湍流摩阻,因此,加热控制能够减小壁面摩阻。同时,从图 2已知,温度控制还会影响湍流区域的摩阻系数。
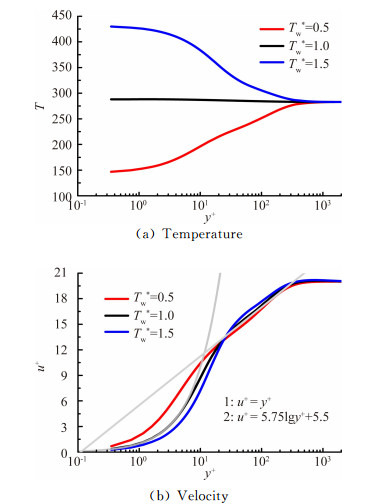
考虑流动为湍流流动时,如当地雷诺数为Rex=2.91×105位置处,边界层内温度和速度分布如图 6所示,图中y+、u+定义如式(5),式中τw为当地壁面摩擦应力。从图中可以看出,温度边界层与速度边界层厚度基本相同,温度控制在边界层内形成的温度梯度,仅影响线性底层(y+ < 5)、过渡区和对数层(30 < y+ < 350),而对湍流边界层对数区以外的区域影响不大[15]。
|
| 图 6 湍流边界层内温度与速度分布 Fig. 6 Variation of temperature and velocity of turbulent boundary-layer |
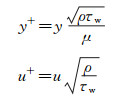
|
(5) |
由图 6可知,壁面加热控制使线性底层内速度斜率变小,即减小了线性底层内的速度梯度,这是因为近壁区内空气粘性作用增强,速度分布更加均匀,如图 7所示。

|
| 图 7 线性底层内速度梯度与粘性系数分布 Fig. 7 Variation of du/dy and viscosity of sub-layer |
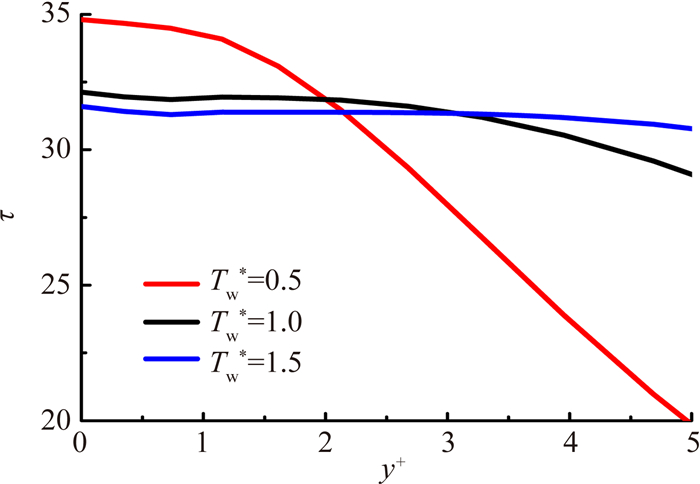
壁面加热控制增大壁面处粘性系数,减小速度梯度,由于壁面附近速度梯度减小幅度更大,根据式(6),平板壁面附近的粘性切应力τ会减小,如图 8所示。因此,壁面加热控制会导致平板壁面摩擦应力τw减小,壁面摩阻系数Cf随之减小,如图 2。
|
| 图 8 线性底层内粘性切应力分布 Fig. 8 Variation of viscosity shear stress of sub-layer |
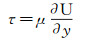
|
(6) |
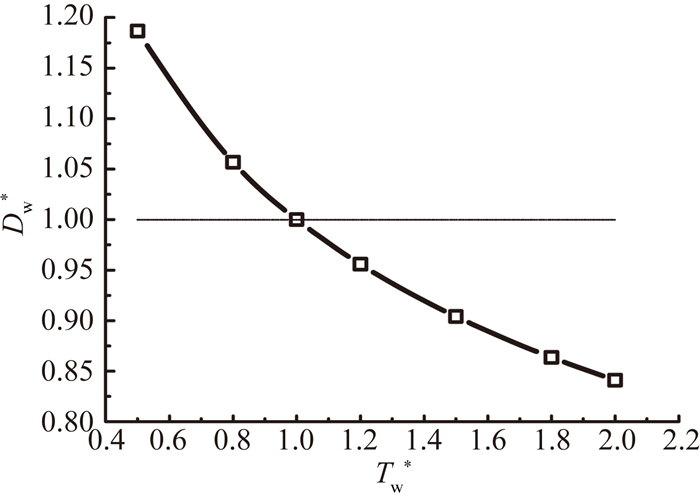
壁面加热能够延迟边界层转捩,同时减小湍流区摩阻系数,因此,壁面加热控制会减小平板总的摩擦阻力,如图 9所示,图 9为平板表面摩擦阻力Dw*在不同控制温度下的变化规律。由图可见,当控制温度从绝热壁面温度288K增大至432K时,摩擦阻力减少约9.6%,减阻效果良好。
|
| 图 9 平板摩擦阻力变化规律 Fig. 9 Variation of drag for flat plate |
3 结论
在低速范围内,采用带有转捩模式的三方程涡粘模型,数值模拟壁面温度控制对零压力梯度平板边界层流动的影响,分析温度控制对平板转捩雷诺数和壁面摩擦阻力的影响规律和原因。主要得出如下结论:
1) 高超声速流动中,通常采用壁面冷却的方式增大转捩雷诺数,而在低速情况下,壁面温度越高,转捩雷诺数越大。这是因为,低速下对平板进行加热后,层流区域温度边界层内粘性系数增大,粘性作用增强,雷诺切应力和湍动能减小,脉动受到抑制,流动更加稳定,转捩雷诺数增大。
2) 壁面温度控制使平板湍流区粘性底层中的速度梯度和壁面附近的粘性切应力变小,进而减小壁面处摩擦应力和摩阻系数。
3) 壁面加热控制能够延迟边界层转捩,扩大层流区,并减小湍流区摩阻,因而减小平板摩擦阻力,壁面温度越高,平板阻力越小。这一结论,与Lin和Kramer等的研究成果一致。
4) 相应地,壁面冷却控制会提前转捩,减小平板转捩雷诺数越大,增大摩擦阻力越小;壁面温度越低,平板转捩雷诺数越小,阻力越大。
| [1] | Green J E. Laminar flow control-back to the future, AIAA 2008-3738[R]. Reston:AIAA, 2008. |
| [2] | Joslin R D. Aircraft laminar flow control[J]. Annual Review of Fluid Mechanics, 1998, 30:1–29. DOI:10.1146/annurev.fluid.30.1.1 |
| [3] | Lin J C, Ash R L. Wall temperature control of low-speed body drag[J]. Journal of Aircraft, 1986, 23(1):93–94. DOI:10.2514/3.45272 |
| [4] | Karamer B R, Smith B C, Heid J P, et al. Drag reduction experiments using boundary layer heating. AIAA-99-0134[R]. Reston:AIAA, 1999. |
| [5] |
Li Yiming, Yan Dachun. Phenomenon of reverse transition on a heated flat plane with stable temperature stratification[J].
Acta Scientiarum Naturalium Universitatis Pekinensis, 2005, 41(3):381–387.
(in Chinese) 李轶明, 颜大椿. 加热平板表面温度分层产生的湍流逆转捩现象[J]. 北京大学学报(自然科学版), 2005, 41(3) : 381–387. |
| [6] |
Zhang Zhen, Sun Zhili, Yan Dachun. Experimental research on the mechanism of reverse transition in turbulent boundary layer[J].
Acta Scientiarum Naturalium Universitatis Pekinensis, 2006, 42(3):305–309.
(in Chinese) 张振, 孙智利, 颜大椿. 湍流边界层逆转捩机制的实验研究[J]. 北京大学学报(自然科学版), 2006, 42(3) : 305–309. |
| [7] | Lees L. The stability of the laminar boundary layer in a compressible fluid[R]. NACA Report 876, 1947. |
| [8] | Boehman L I, Mariscalco M G. The stability of highly cooled compressible laminar boundary layers[R]. AFFDL Tech. Rept, 1976:76-148. |
| [9] | Potter J L. Review of the influence of cooled walls on boundary-layer transition[J]. AIAA J., 1980, 18(8):1010–1012. DOI:10.2514/3.7703 |
| [10] | Spyridon G, Lekoudis. Stability of the boundary layer on a swept wing with wall cooling[J]. AIAA J., 1980, 18(9):1029–1035. DOI:10.2514/3.50852 |
| [11] | Hall P, Morris H. On the instability of boundary layers on heated flat plates[M]. National Aeronautics and Space Administration, Langley Research Center, 1991. |
| [12] | Sameen A, Govindarajan R. The effect of wall heating on instability of channel flow[J]. Journal of Fluid Mechanics, 2007, 577:417–442. DOI:10.1017/S0022112007004636 |
| [13] | Walters D K, Davor C. A three-equation eddy-viscosity model for Reynolds-averaged Navier-Stokes simulations of transitional flow[J]. Journal of Fluids Engineering, 2008, 130-121401-1. |
| [14] | Coupland J. ERCOFTAC Special interest group on laminar to turbulent transition and retransition:T3A and T3B test cases[R]. A309514, 1990. |
| [15] |
Tian Yan, Jiang Nan. Experimental investigation of effects of temperature boundary layer on multi-scale coherent structures in wall turbulence[J].
Journal of Aerospace Power, 2007, 22(6):980–985.
(in Chinese) 田砚, 姜楠. 温度边界层对壁湍流多尺度相干结构的影响[J]. 航空动力学报, 2007, 22(6) : 980–985. |


