风洞试验完全模拟飞行雷诺数一直是制约我国大型飞机研制的一个瓶颈。大飞机许多关键流动现象与雷诺数紧密相关,如转捩、分离等。雷诺数模拟不足,阻力、最大升力系数等气动特性与实际飞行情况相比误差较大,依靠外插可能会导致意想不到的结果。通过低温、增压方式,可以提高风洞雷诺数模拟能力,国外ETW、NTF、KKK等风洞应用该技术可以模拟全尺寸真实飞行雷诺数,我国正在建设低温高雷诺数风洞,其试验雷诺数覆盖民机巡航雷诺数,可大幅提升我国大飞机气动研究和设计能力。
低温风洞要求作为运行介质气体的温度在110~320K范围,气体处于该低温段范围时会出现真实气体效应,其状态不满足完全气体假设。与完全气体相比,低温真实气体效应对飞行器气动特性的影响如何,以及该影响与雷诺数影响相比所占比例的大小均为研究中所不可回避的问题。国内外研究对此没有一个明确的结论。本文针对该问题,利用数值模拟手段进行研究,以期为低温风洞试验数据修正提供参考。
描述低温真实气体最精确的方程是以级数形式表达的维里方程[1]。该方程通过不断增加项数,可以很精确地描述气体属性,但维里方程过于复杂,编程实现比较困难。一般来说,三次方程形式的状态方程在任意气体、液体的描述中应用已经很广,其精度满足常规研究要求。因此对于低温真实气体状态方程,本文选取了三次方程中的Aungier-Redlich-Kwongz方程[2](以下简称ARK方程),并通过与NIST数据[3]对比,验证该状态方程描述低温高压真实气体的精度。
本文发展了任意状态方程的流动数值模拟方法,其雅克比矩阵、声速等状态参数均以偏导数形式表示。在此基础上,应用ARK方程,以氮气为介质,模拟跨声速及低速条件下,真实气体效应对运输机构型气动特性的影响,同时模拟雷诺数变化对运输机构型的气动特性的影响,对真实气体效应和Re数效应进行对比分析。
1 模型与方法 1.1 控制方程为兼顾高速和低速流动数值模拟,低温高压和常温常压气体流动控制方程均采用预处理雷诺平均N-S方程:
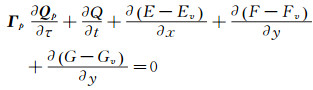
|
(1) |
其中: Q为守恒变量,Qp为原始变量,E、F、G为无粘通量,Ev、Fv、Gv为粘性通量,具体形式见文献[4]。
为使控制方程封闭,必须引入热状态方程和量热状态方程,常温常压气体可以假设成完全气体,其热状态方程为:
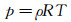
|
(2) |
量热状态方程为
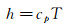
|
(3) |
而对于考虑真实气体效应的低温高压气体,其热状态方程可选择ARK方程,相应的量热状态方程通过热力学关系式推导获得。
1.2 ARK状态方程
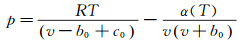
|
(4) |
式中:
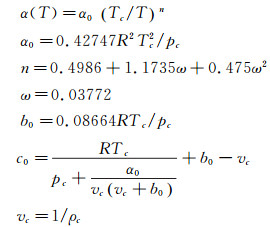
|
(5) |
氮气临界参数:
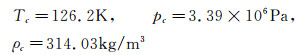
|
(6) |
应用热力学关系式及偏离函数概念[6],推导可得焓的解析表达式:
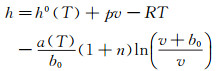
|
(7) |
h
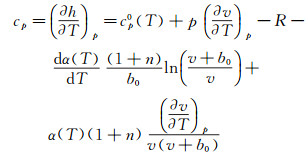
|
(8) |
其中cp0为完全气体的定压比热系数。文献中分别用了5系数、7系数的插值公式[7-8],但其适用温度的范围均为200~6000K。经研究对比发现,5系数的状态方程在低温条件下与NIST数据吻合更好。对于氮气的粘性系数及热传导系数,在本文所计算的温度范围内可以采用萨斯兰公式[9]。
应用ARK方程后,声速表达式可以由热力学关系推导得到:
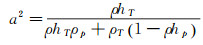
|
(9) |
通过对自主研制的亚跨超流场求解软件pmb3d进行适当改造,得到了适合低温高压气体流动的求解软件。软件采用隐式LUSGS对方程(1)进行时间离散,应用Roe格式进行空间对流项离散,采用中心格式进行粘性项离散,湍流模型采用k-ω SST两方程模型,并以均匀来流作为计算的初场。所涉及的边界条件包括远场边界、固壁边界、对称边界、奇性轴边界等,相关处理见计算流体力学书籍。
ARK状态方程(4)可以改写为以比容为未知量的三次方形式:
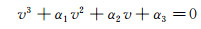
|
(10) |
式(10)可用牛顿切线法求解,以理想气体方程比容为初值,迭代5~8步即可。在本文所考虑的温度、压力范围内式(10)为单解。
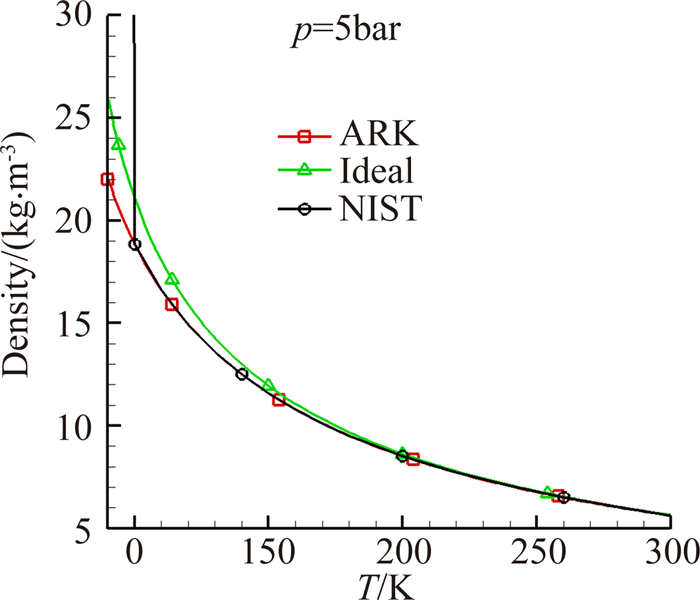
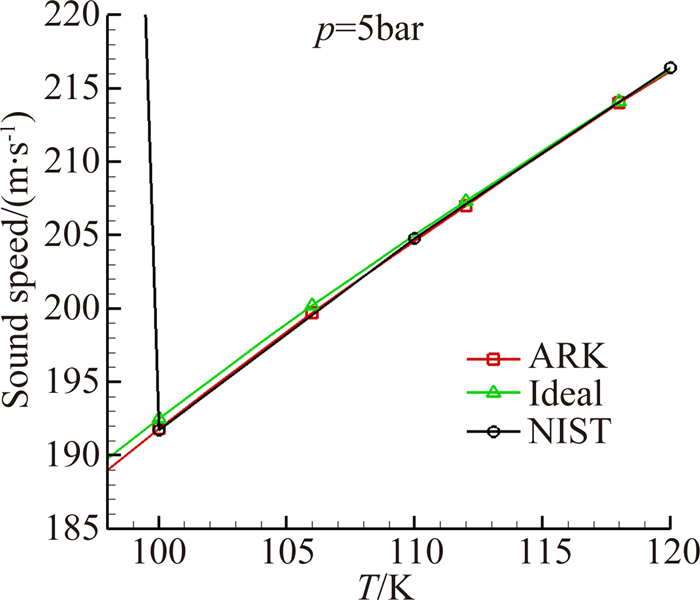
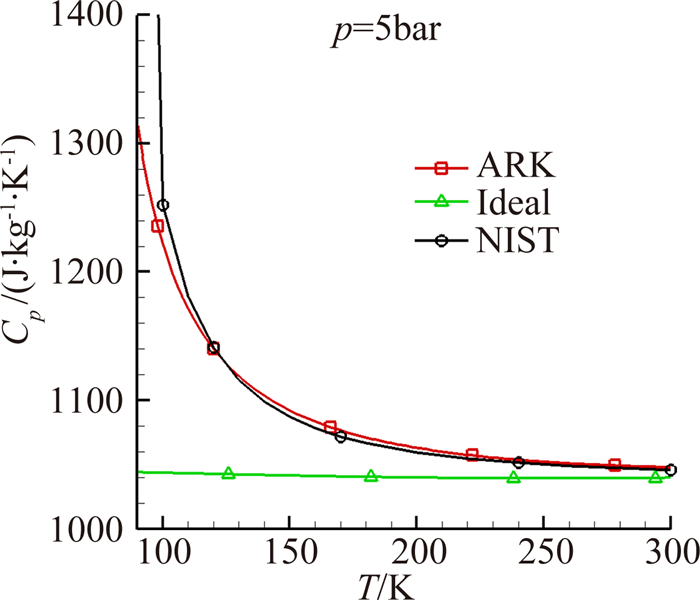
2 计算结果及讨论 2.1 低温高压氮气状态方程精度考核考虑到一般低温增压风洞运行的总温范围为110~323K,总压范围为:0.2~4.5bar。一般而言,压力越大、温度越低,真实气体效应越明显。因此本文采用ARK状态方程和理想气体状态方程计算了5bar压力条件下几种典型的热力学物理量随温度的变化曲线,并与NIST数据进行了对比。
在本文基于任意气体状态方程的模拟方法中,所用到的与真实气体效应相关的参数为定压比热、密度及声速。从图 1~图 3曲线看,当温度在200K以下,上述物理量在理想气体与真实气体条件下差别较大,而ARK方程描述的曲线与真实气体吻合很好。在所涉及的温度、压力范围内,相关曲线的最大误差在0.3%以下。因此,ARK方程对气体状态描述的精确性满足数值模拟要求。
|
| 图 1 密度随温度变化曲线 Fig. 1 Density curve following with temperature |
|
| 图 2 声速随温度变化曲线 Fig. 2 Sound speed curve |
|
| 图 3 定压比热随温度变化曲线 Fig. 3 Specific heat curve under constant pressure |
2.2 数值模拟方法的验证
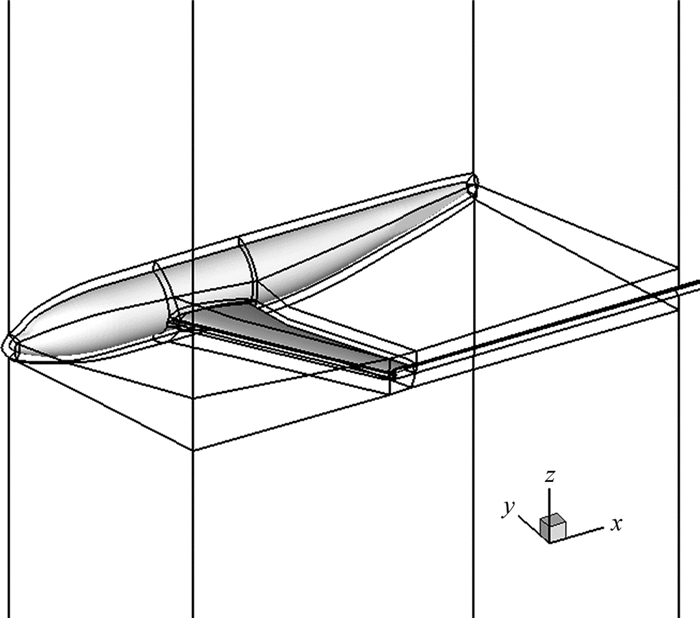
计算构型和网格均采用第二届AIAA阻力会议提供的翼身组合体DLRF6标模[5],其网格拓扑见图 4,共包含21块计算块,共计1300万网格点。在雷诺数3×106~2×107范围内y+ < 1,满足粘性计算网格法向最小间距要求。为了验证改造后程序的计算精度,本文针对表 1算例,以氮气为流动介质,与以空气为流动介质的pmb3d及美国NASA主力软件CFL3D、OVERFLOW的计算结果进行对比分析。
|
| 图 4 DLRF6空间网格 Fig. 4 Grid of DLRF6 configuration |
| Property | Value |
| S/2 | 72700mm2 |
| c | 141.2mm |
| b/2 | 585.647 mm |
| AR | 9.5 |
| Xref | 157.9mm |
| Yref | 0.0mm |
| Zref | -33.92 mm |
| M des | 0.75 |
| CLdes | 0.5 |
| Rec | 3×106 |
| M∞ | 0.75 |
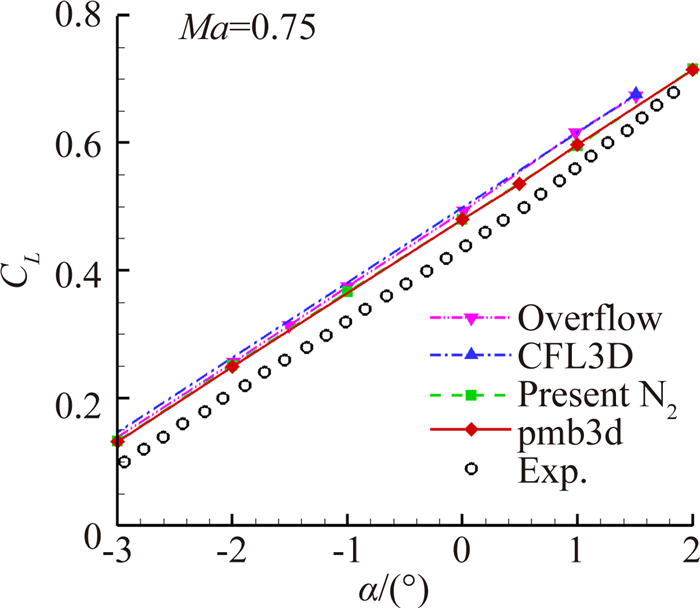
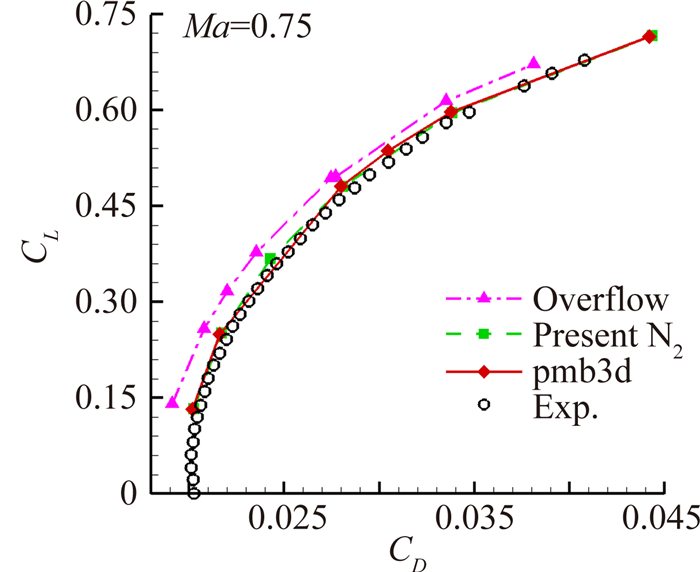
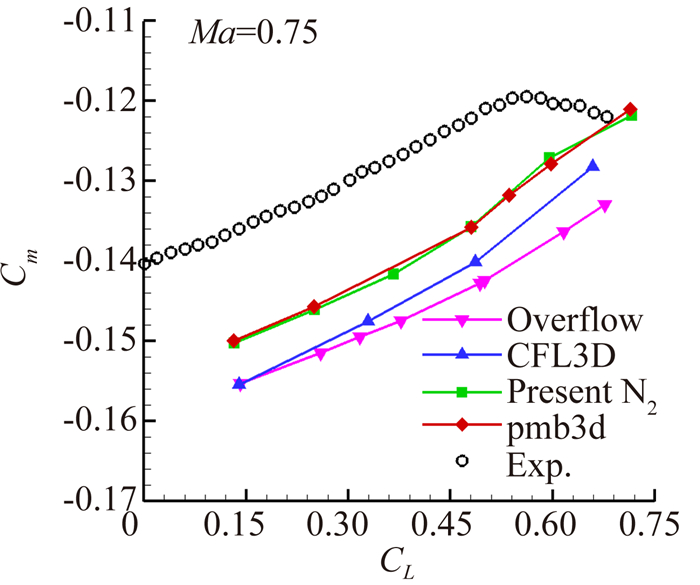
由图 5~图 7中对比曲线看到,在常温常压条件下,本文发展的数值方法求解结果基本回归到pmb3d软件计算结果,计算精度与国外软件相当,同时表明常温常压下选用空气组分和氮气组分对计算结果影响很小。
|
| 图 5 升力系数随迎角变化曲线 Fig. 5 Lift coefficient curves vary with angle of attack |
|
| 图 6 升力系数随阻力系数变化曲线 Fig. 6 Lift coefficient curves vary with drag coefficient |
|
| 图 7 俯仰力矩系数随升力系数变化曲线 Fig. 7 Pitch moment coefficient curves vary with lift coefficient |
2.3 真实气体效应对气动特性的影响分析
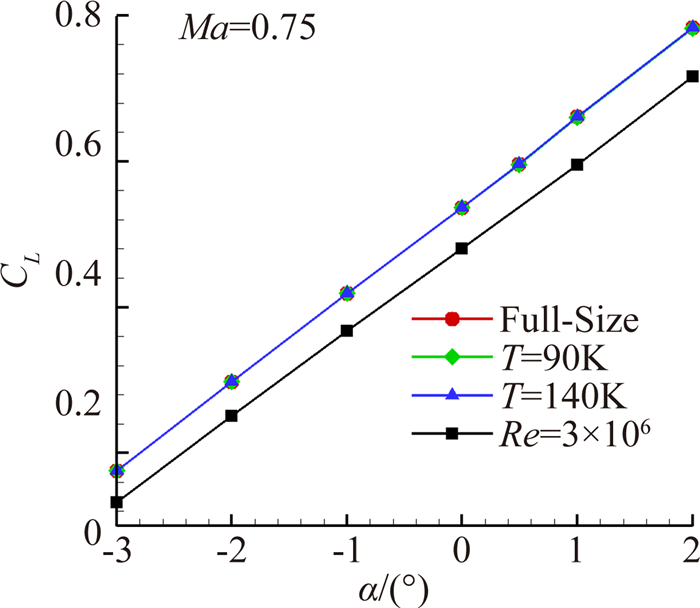
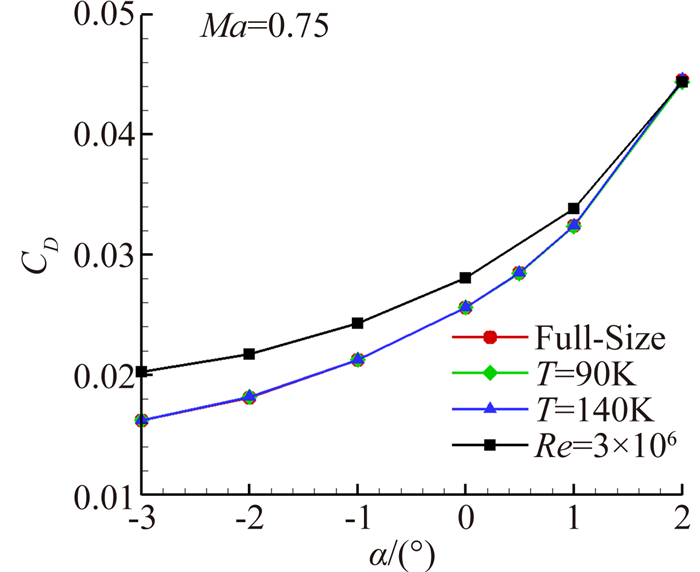
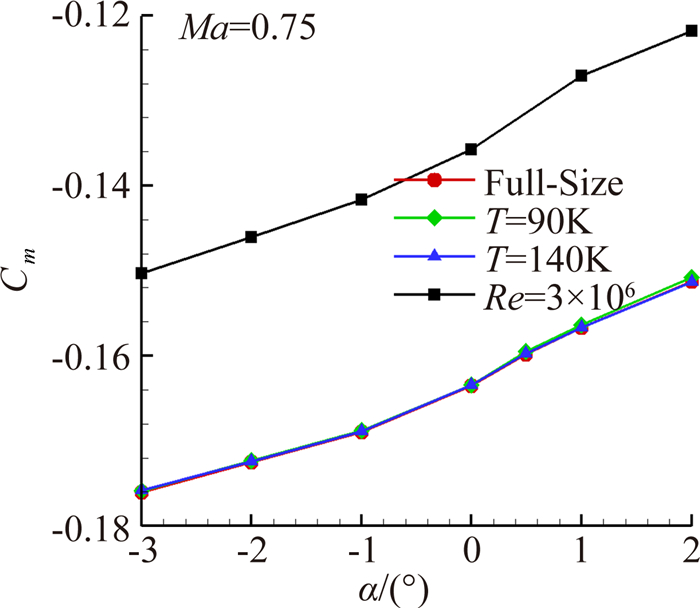
考虑到一般运输机真实飞行雷诺数为2×107量级,以Ma=0.75,Re=2×107条件研究巡航状态真实气体效应影响具有代表性。首先利用软件模拟10km高空全尺寸飞机构型气动性能(表 2工况1,介质为氮气),然后模拟了低温风洞中缩尺模型在满足马赫数0.75、雷诺数2×107条件的两种状态下(表 2分别对应静温90K、140K)考虑真实气体效应的流动,将二者气动特性作对比分析以研究真实气体效应的影响。为比较真实气体效应影响与Re数影响的相对大小,工况4计算了将工况1模型缩比,雷诺数降至3×106时标模的气动特性。
| 工况 | V /(m·s-1) | P /(105Pa) | T /K | Lref/m |
| 1 | 228.3266 | 0.2608 | 223.1 | 3.1440 |
| 2 | 138.4684 | 1.5885 | 90 | 0.1412 |
| 3 | 178.5714 | 3.0274 | 140 | 0.1412 |
| 4 | 228.3266 | 0.2608 | 223.1 | 0.4716 |
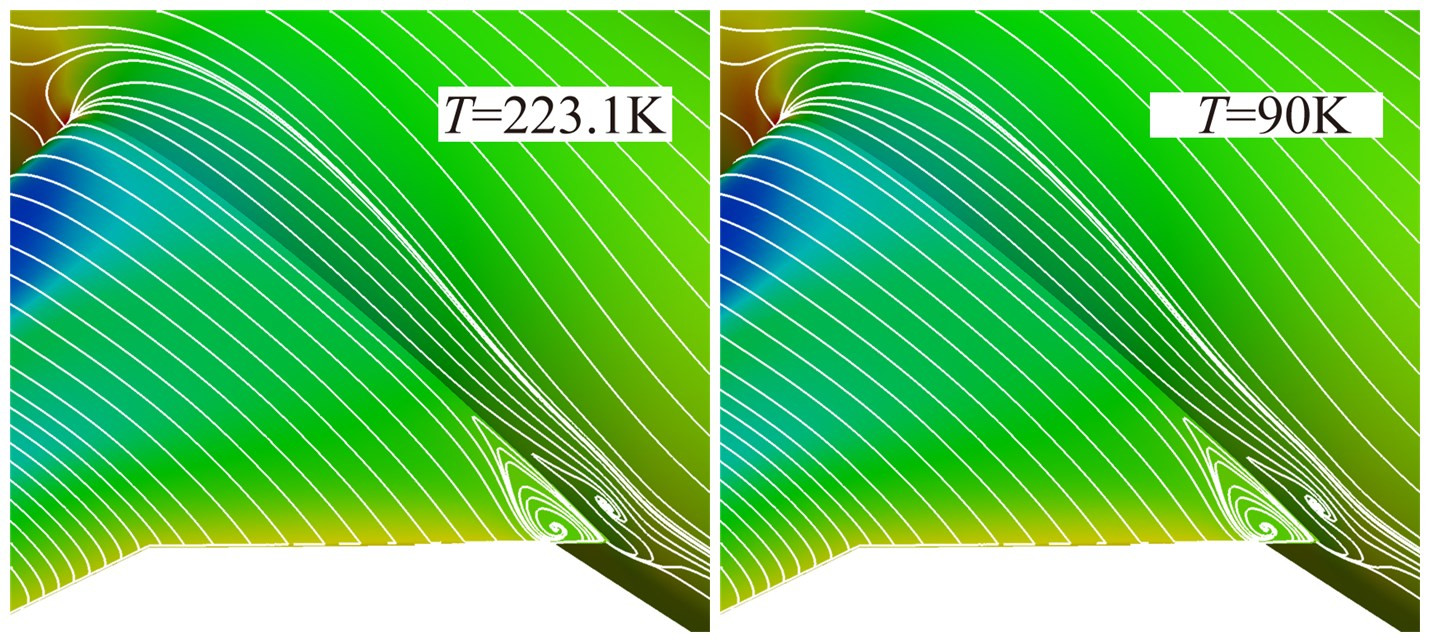
图 8~图 10显示了四种结果的比较。从图中可以看到,在马赫数、雷诺数一致的情况下,升力、阻力、俯仰力矩计算结果非常一致。从具体计算数据分析,在所考虑的迎角范围,三种状态阻力最大差别为1count,力矩曲线相对差量约0.3%,表明在低温风洞运行的温度范围内真实气体效应对运输机构型气动特性的影响很小。图 11显示了有无真实气体效应翼身结合部流动分离的比较,二者无明显差别。图 8~图 10同时表明,Re数差别近一个量级时,气动特性的差异是非常显著的。
|
| 图 8 升力系数曲线比较 Fig. 8 Comparison of lift coefficient curve |
|
| 图 9 阻力系数曲线比较 Fig. 9 Comparison of drag coefficient curve |
|
| 图 10 俯仰力矩系数曲线比较 Fig. 10 Comparison of pitch moment coefficient curve |
|
| 图 11 翼身结合部分离流场比较 Fig. 11 Comparison of flow separation |
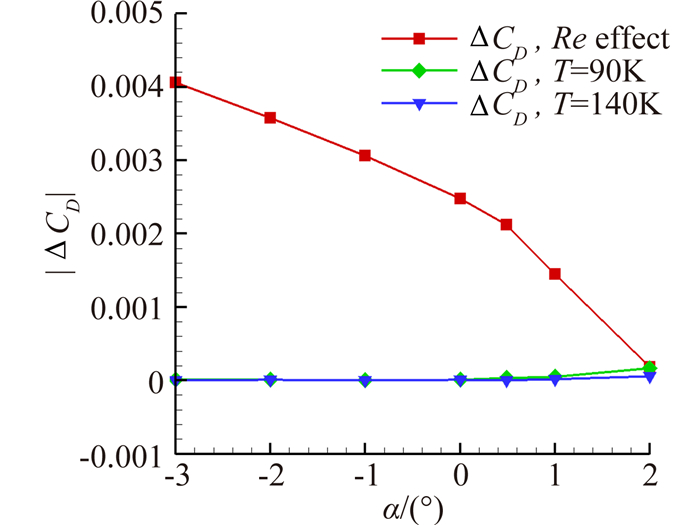
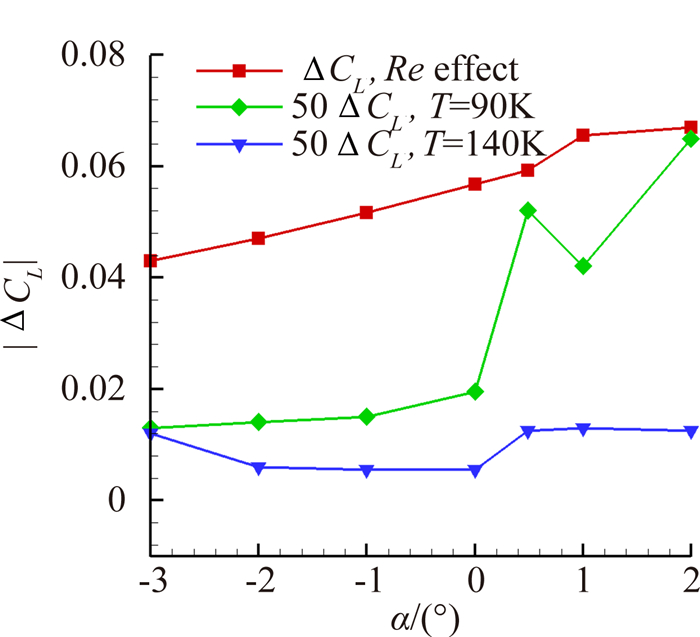
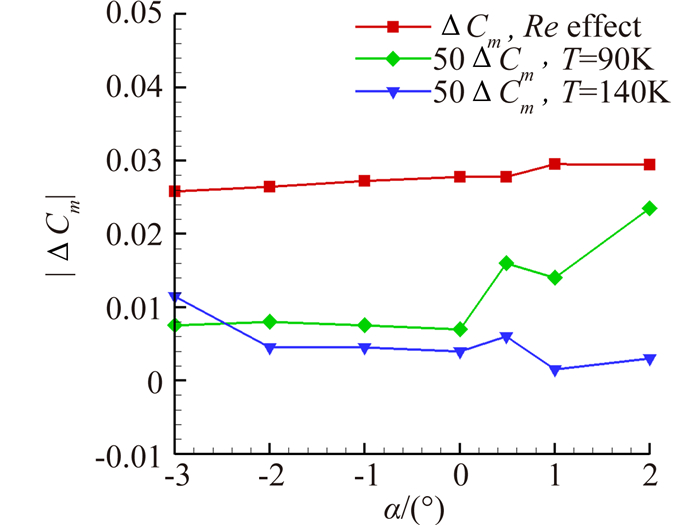
图 12~图 14显示了雷诺数效应和低温真实气体效应对气动特性影响差量的对比。图中|ΔCL|分别为工况2/3/4与工况1升力系数差量,其余阻力、力矩类似。从图中可看出,与Re效应的影响相比,真实气体效应对阻力的影响远小于Re效应影响量,2°时两者接近是因为此时两组雷诺数计算曲线相交。对升力和力矩的影响最大约为Re效应影响量的2%。
|
| 图 12 Re效应与真实气体效应对阻力影响 Fig. 12 Comparison of Re effect and real gas effect on drag |
|
| 图 13 Re效应与真实气体效应对升力影响 Fig. 13 Comparison of Re effect and real gas effect on lift |
|
| 图 14 Re效应与真实气体效应对俯仰力矩影响 Fig. 14 Comparison of Re effect and real gas effect on pitch moment |
本文同时对低速状态下真实气体效应与Re数效应对运输机气动特性的影响作了对比分析,所选择的计算状态见表 3。计算分3组状态,来流马赫数均为0.2,第1组状态为常温常压,模型为全尺寸,雷诺数为Re=2×107;第二组仍然为常温常压,外形缩比为1:10,雷诺数为Re=2×106。第3组状态考虑风洞模型,低温增压,雷诺数为Re=2×107。
| V /(m·s-1) | P /atm | T /K | L /m | ReL | |
| 1 | 69.21 | 1.0 | 288.15 | 4.2271 | 2×107 |
| 2 | 69.21 | 1.0 | 288.15 | 0.4227 | 2×106 |
| 3 | 41.17 | 4.4 | 110.00 | 0.2502 | 2×107 |
从图 15~图 17中可以看到,马赫数与雷诺数一致时,气动力曲线几乎重合,表明真实气体效应影响极其微小,真实气体效应对失速迎角也基本无影响。曲线同时表明雷诺数从百万量级增加到千万量级时,升力系数增大,升力线斜率略増,失速推迟,最大升力系数增大,阻力降低,符合雷诺数影响一般规律。图 18~图 20显示了低速状态时雷诺数效应和低温真实气体效应对气动特性影响差量的对比。从图中可看出,与雷诺数效应对气动特性的影响相比,真实气体效应对阻力、升力的影响量约为雷诺数效应影响量的1%,对力矩的影响量约为雷诺数效应影响量的2%。
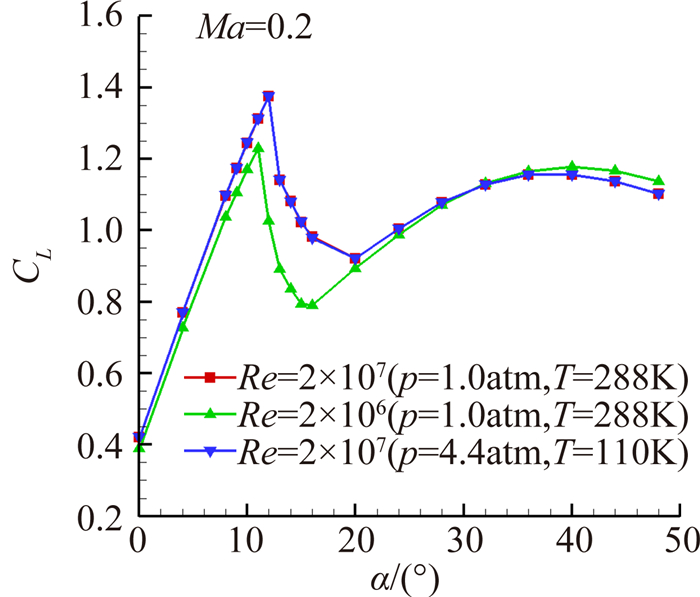
|
| 图 15 升力系数曲线比较 Fig. 15 Comparison of lift coefficient curve |

|
| 图 16 阻力系数曲线比较 Fig. 16 Comparison of drag coefficient |
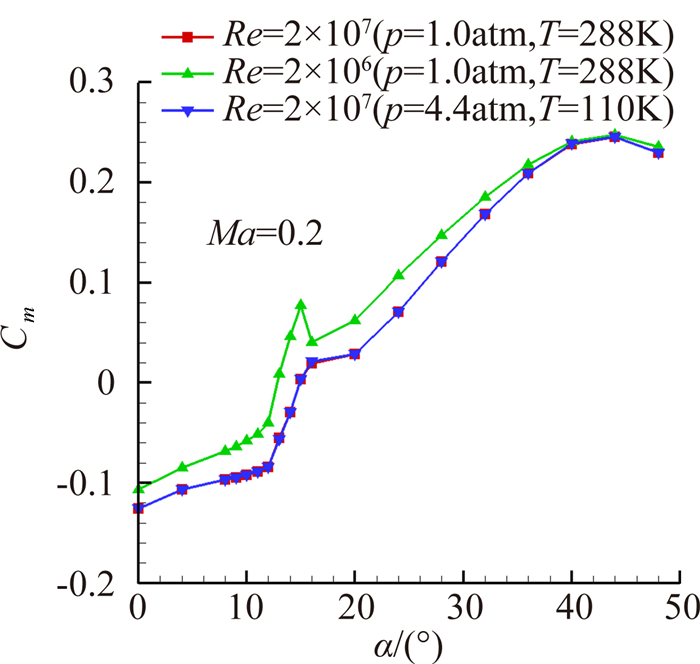
|
| 图 17 俯仰力矩系数曲线比较 Fig. 17 Comparison of pitch moment coefficient |

|
| 图 18 Re效应与真实气体效应对阻力影响 Fig. 18 Comparison of Re effect and real gas effect on drag |
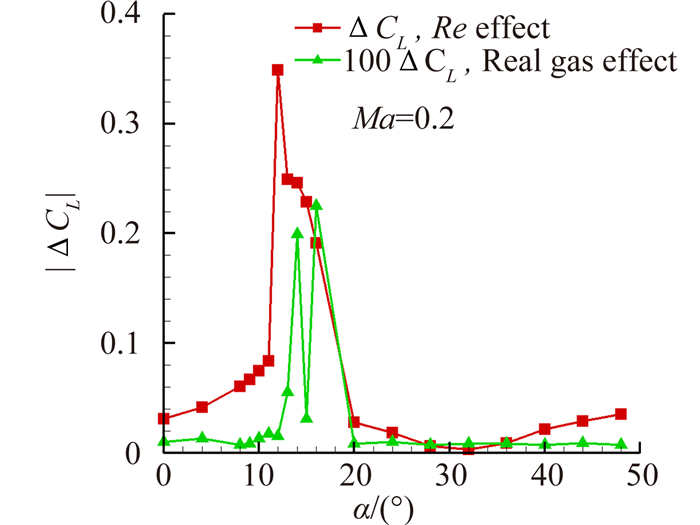
|
| 图 19 Re效应与真实气体效应对升力影响 Fig. 19 Comparison of Re effect and real gas effect on lift |
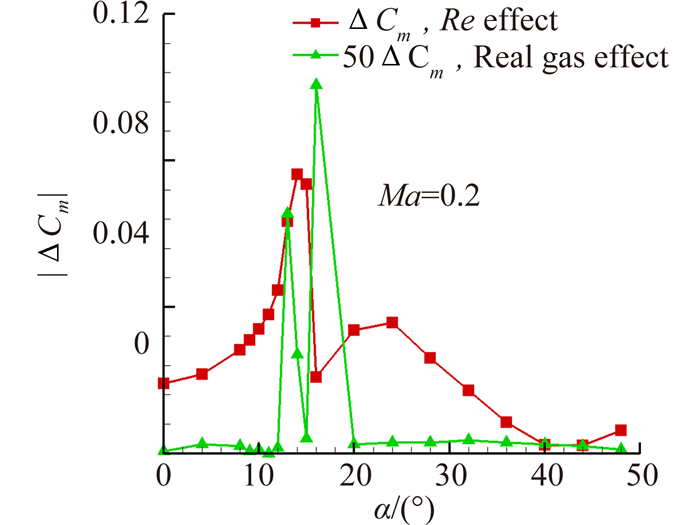
|
| 图 20 Re效应与真实气体效应对俯仰力矩影响 Fig. 20 Comparison of Re effect and real gas effect on pitch moment coefficient |
3 结论
本文应用ARK状态方程,开发了考虑低温氮气真实气体效应的模拟软件。通过与NIST数据对比,表明本文所选用的状态方程可以精确模拟氮气低温真实气体效应。该软件对DLRF6外形进行了数值模拟,并与国外软件及试验数据进行对比,结果表明,本文计算方法正确,结果合理。
本文研究表明,在低温高压条件下,理想气体状态方程与真实气体状态方程差别较大,但在所涉及的压力和温度范围内,真实气体效应对运输机气动特性影响很小,与雷诺数效应影响相比,则可以忽略,以氮气为介质的低温风洞试验研究可以采用完全气体假设。
| [1] | Epstein P S. Textbook of thermodynamics[M]. New York, London: John Wiley & Sons, Inc, 1961 . |
| [2] | Augnier R H. A fast accurate real gas equation of state for fluid dynamics analysis applications[J]. Journal of Fluids Engineering, 1995, 117:277–281. DOI:10.1115/1.2817141 |
| [3] | Jacobsen R. The thermodynamic properties of Nitrogen from 65 to 2000K with pressures to 10000 atmospheres[D]. USA:Washington State University, 1972. |
| [4] | The National Institute of Standards and Technology (NIST). Thermophysical properties of fluid systems[EB/OL]. http://webbook.nist.gov/chemistry/fluid/ |
| [5] | ANSYS, Inc.ANSYS CFX-Solver theory guide[M]. November 2013. |
| [6] | Invernizzi C M. Thermodynamic fundamentals and applications[M]. London: Springer-Verlag, 2013 . |
| [7] | McBride B J, Zehe M J, Gordon S. NASA Glenn coefficients for calculating thermodynamics properties of individual species[R]. NASA TP-211556, 2002. |
| [8] | McBride B J, Gordon S, Reno M A. Coefficients for calculating thermodynamic and transport properties of individual species[R]. NASA TM-4513, 1993. |
| [9] | WhiteF M. Fluid mechanics[M]. 北京: 机械工业出版社, 1982 . |
| [10] | Poschner M, Zimmermann I, Pfitzner M. CFD simulation of the combustion process in the mascotte facility under supercritical conditions[C]//21st ICDERS, 2007. |
| [11] | ANSYS, Inc. ANSYS Fluent user's guide[M]. November 2013. |
| [12] | Maria Grazia De Giorgi, Alessio Leuzzi. CFD simulation of mixing and combustion in LOX/CH4 spray under supercritical conditions[C]//39thAIAA Fluid Dynamics Conference. San Antonio, Texas:2009. AIAA 2009-4038. |



