以吸气式发动机为动力的高超声速巡航飞行器采用具有尖化前缘特征的高升阻比外形,长时间在大气层内高超声速飞行,前缘部位需要保持结构完整,需实现非烧蚀热防护(如美国X-43、X-51等)。此类飞行器尖前缘部位承受的热环境恶劣,气动加热分布极不均匀,尖前缘驻点部位因高温或热应力破坏的风险较高,传统防热技术实现非烧蚀的难度很大。
中国航天空气动力技术研究院针对这种尖化前缘特征的非烧蚀热防护需求,提出了一体化高温热管疏导式热防护技术方案[1-2]。方案将整个尖前缘结构设计为一体化结构,突破了热管冷却前缘防热面板的传统思路,热管的壳体即防热面板。该方案充分利用热管高效传热、等温性极佳的特点,可有效将尖前缘驻点高热流区的热量快速传输至尾端低热流区,从而有效降低前缘驻点温度,实现非烧蚀[3]。
高温热管在防热设计与应用上面临的一个主要困难是其启动问题[4-7],若热管未启动,其热疏导性能无法发挥,可能引起前缘部位热防护结构的局部破坏,因此需要开展启动特性研究。高温热管通常使用碱金属作为工作介质(钠、钾、锂等),常温下碱金属为固态,即热管处于“冻结状态”,“冻结状态”的高温热管若无法启动,有局部高温破坏风险,因此需建立一种适合用于分析尖前缘一体化高温热管在气动加热环境下启动性能的计算方法并开展计算分析,为尖前缘高温热管工程设计与性能评估提供方法和依据。
高温热管启动过程是热管从“冻结状态”到内部形成连续蒸汽流动的过程,在这一过程中,热管内部多种传热传质机制的相互耦合关系复杂,很难获得解析解,而数值模拟则需要大量时间用于发展模型和数值计算[8]。Cao和Faghri[9]根据高温热管启动过程的温度分布特征,采用“温度锋面”模型,导出了均匀受热圆柱高温热管启动过程的代数方程组,计算结果与试验数据、数值计算结果均符合较好。国内学者也通过简化分析、试验测试以及数值模拟等方法开展了对热管启动性能及传热性能的相关研究[10-13],但还未有针对尖前缘一体化高温热管启动性能研究的公开报道。另外,由于尖前缘高温热管所处环境属于瞬态非均匀气动加热环境,且热管外形为不规则外形,因此数值模拟研究的难度很大。
本文基于高温热管启动模拟的“温度锋面”模型,建立了一种适合用于飞行器尖前缘一体化高温热管在气动加热环境下启动性能的工程计算方法并完成了相应的试验验证,最后针对此类高温热管的启动性能影响因素进行了计算分析,提出了减小高温热管启动时间的方法和途径,可为以吸气式发动机为动力的高超声速巡航飞行器尖前缘防热设计或改进提供理论指导。
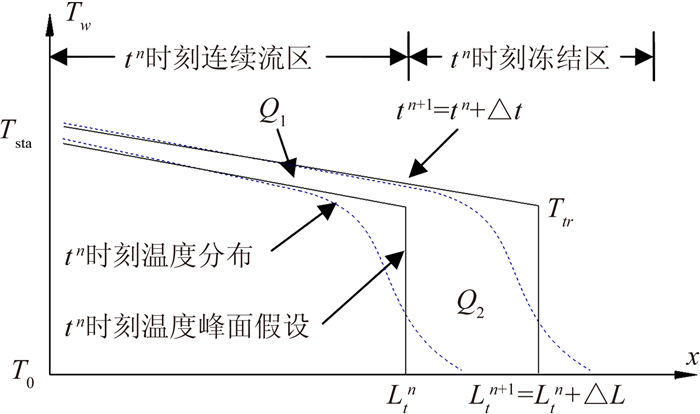
1 物理模型及假设高温热管启动过程是指热管在受热状态下,内部逐渐形成连续蒸汽流动的过程。试验研究表明,在较高热流输入条件下,高温热管蒸发段(或加热段)温度会迅速上升,同时在蒸发段末端形成一个明显的温度梯度并向热管尾端移动[14],即高温热管启动过程的“温度锋面”模型。如图 1所示,该模型将高温热管划分为了两个区域,高温连续蒸汽流区和冻结区(非连续蒸汽流区),两个区域的界面称作“温度锋面”,假设连续蒸汽流区温度沿热管轴向保持线性分布且温度锋面保持为连续蒸汽流转换温度Ttr,驻点温度Tsta随温度锋面推进而逐渐提升,在没有外加热源的情况下冻结区域保持为环境温度T0,蒸发段吸热使得Δt时间内热管的“温度锋面”位置Lt向尾端移动距离ΔL。由于高温热管壳体较薄,可近似认为在任意长度L处蒸汽温度与壳体温度相等。
|
| 图 1 热管启动过程“温度锋面”模型示意图 Fig. 1 Schematic of the flat-front startup model for heat pipe |
2 热管启动的工程计算方法
飞行器前缘高温热管沿轴向各个位置均要承受不同程度的气动加热,不存在明显的蒸发段/绝热段/冷凝段分区,不能按照文献[9]的方法获得热管启动过程的解析解,因此考虑针对前缘热管的热环境特点进行沿轴向节点划分,并对每一个节点的气动加热率、温升速率以及蒸汽流动状态进行计算,然后采用区域能量守恒对温度锋面的位置及其推进距离进行计算。
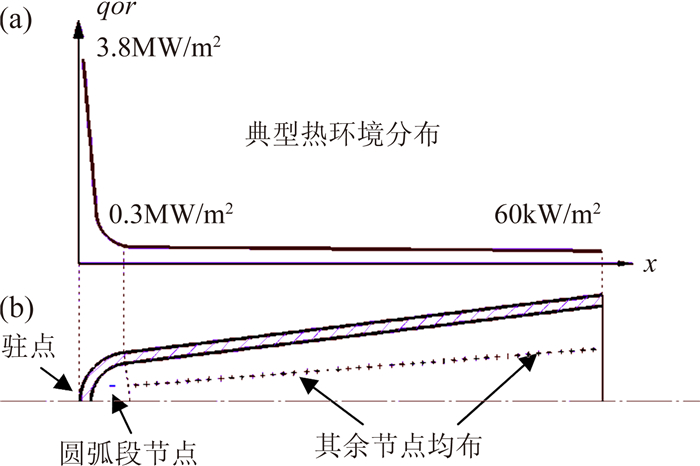
2.1 节点划分方法图 2(a)为典型飞行器楔形尖前缘外形及其表面气动加热热流密度沿轴向的分布规律。可以看出高热流区集中在距离前缘驻点极小的范围内(通常为楔形前缘的圆弧段)。根据尖前缘热管气动加热热流分布的这一特征,近似将热管圆弧段看作初始蒸发段,并作为第一个节点,从圆弧段出口至热管尾端采用均布节点,如图 2(b)所示。
|
| 图 2 前缘热管热环境分布特征及节点划分示意 Fig. 2 Typical thermal environment distribution and node partition of sharp leading edge heat pipe |
在气动加热环境下,第一个节点会迅速温升并形成连续蒸汽流,即在圆弧段出口形成初始“温度锋面”,并不断向热管尾端推移,后续节点的温升热量来源主要来自连续蒸汽流携带的汽化潜热。驻点至“温度锋面”的区域为连续蒸汽流区,“温度锋面”至尖前缘尾端的区域为冻结区。
2.2 连续蒸汽流转换温度计算方法高温热管连续蒸汽流转换温度是指在热管有限空间的某一截面位置,随着温度的升高,热管腔内蒸汽由自由分子流转变为连续蒸汽流的转换温度。热管的高效传热依赖于内部碱金属的蒸发、流动和冷凝过程,因此只有形成了连续蒸汽流动,热管高效传热特点才能实现。热管的启动过程可近似看作内部连续蒸汽流区域自加热端向冷凝端不断扩充的过程,“温度锋面”的温度即热管当前截面位置连续蒸汽流的转换温度。
高温热管连续蒸汽流转换温度与碱金属工质类型、蒸汽通道特征尺寸密切相关。通常使用努森数(Kn)来判断热管内部蒸汽流动状态,取Kn≤0.01对应连续蒸汽流。在给定温度条件下,连续蒸汽流形成的转换温度Ttr和通道特征尺寸D对应关系为[9]:
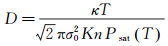
|
(1) |
其中,T为当前截面温度;κ为波尔兹曼常数;σ0为分子特征直径(Na分子取3.567Å,Li分子取4.44Å);Psat为碱金属饱和蒸汽压。
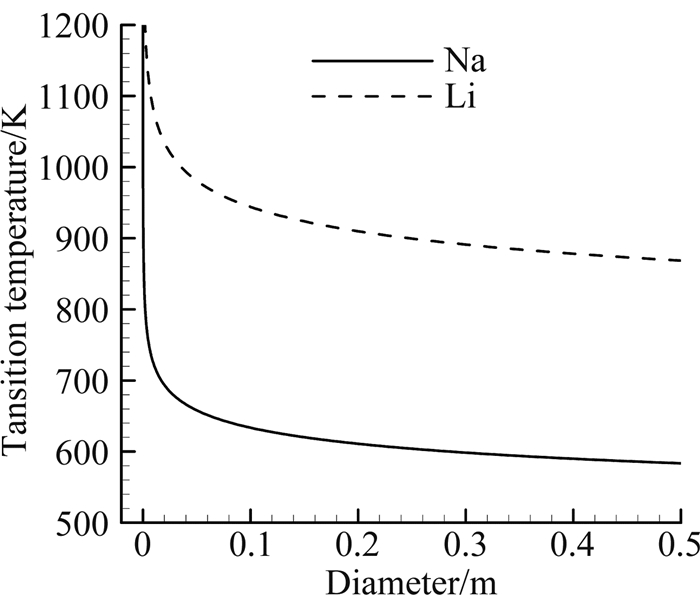
使用式(1)可求解得当前截面的连续蒸汽流转换温度,如图 3所示。对于楔形热管,通道特征尺寸可近似取为通道截面等效直径。
|
| 图 3 碱金属连续蒸汽流转换温度 Fig. 3 Transition temperatures for liquid-metal vapor flow |
2.3 连续流区温度分布计算方法
基于“温度锋面”模型中连续流区为线性分布的近似假设,在计算得到热管截面连续蒸汽流转换温度的情况下,仅需计算连续流区驻点至温度锋面位置的温差即可得到连续流区温度分布。
根据Cotter的热管理论[15],热管连续流区域的层流蒸汽压降近似表示为:
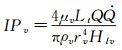
|
(2) |
其中,μv为蒸汽的动力粘度;Lt为连续流区的轴向长度;
在连续流区温度和压力变化不大的情况下,由克劳修斯-克拉贝龙方程积分可得:
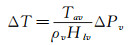
|
(3) |
其中,Tav为连续流区平均温度。
综合式(2)、(3)可得:
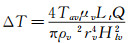
|
(4) |
热管连续流区的传热量Q取当前时刻热管截面的最大传热量,即连续流区所有气动加热进入热管的净热流的总和。
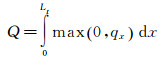
|
(5) |
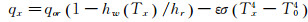
|
(6) |
其中,qx表示热管轴向位置x处单位长度的气动加热净热流;qor为冷壁热流;hr为恢复焓;hw(Tx)为热管壳体表面的壁焓;ε为热管表面发射率;σ为黑体辐射常数。
对于确定的温度锋面位置,使用两式(4)、(5)可迭代求出当前时刻的连续流区的温度分布。这里需指出的是,由于前缘热管为非等截面外形,各个截面连续流转换温度各不相同,若计算得到的节点温度小于该节点的连续流转换温度,为确保节点处于连续蒸汽流动状态,该节点的温度值应取为连续流转换温度,并用该温度作为计算“温度锋面”推进距离的输入条件。
2.4 冻结区节点温度计算方法在热管启动过程中,由于连续蒸汽流区气动加热全部用于“温度锋面”的推进,因此冻结区节点温升的热量来源
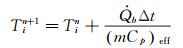
|
(7) |
其中,Tin+1、Tin分别为tn+1、tn时刻的节点温度;Δt为时间步长;(mCp)eff为节点的等效热容。
若Tin小于工质熔点Tmelt,则:
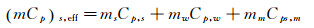
|
(8) |
若Tin大于工质熔点Tmelt,则:
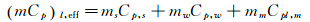
|
(9) |
其中,ms、mw、mm分别为各节点壳体、吸液芯、工质的质量;Cp, s、Cp, w、Cps, m、Cpl, m分别为壳体、吸液芯、固态工质、液态工质在相应温度的比热容。
若在某一时刻固态工质达到了熔点Tmelt,需考虑相变吸热对节点温升的影响。首先计算当前时刻可用于熔化工质的热量Qfusn:
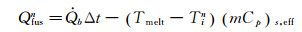
|
(10) |
若Qfusn-mmHsl≥0,表示在当前时间步内,节点内工质能完全熔化,则:
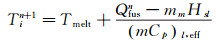
|
(11) |
其中,Hsl为单位质量工质熔化热。
若Qfusn-mmHsl < 0,表示当前时间步内节点工质不能完全熔化,即节点处于熔融状态,且Tin+1=Tmelt,在下一时间步计算中,需继续将“Qfusn+1”与“mmHsl-Qfusn”比较作为判断工质能否完全熔化的依据,同时将式(11)中的熔化热项“mmHsl”替换为熔化还需要热量“mmHsl-Qfusn”。
2.5 温度锋面推进过程计算方法采用区域能量守恒方法计算温度锋面推进距离ΔL。即Δt时间内,温度锋面推进距离需满足“气动加热量Qinput与连续流区tn时刻温升至tn+1时刻所需热量Qneed相等”的能量守恒条件。
由式(6)可知,进入热管的净热流与热管表面温度有关。因此,需首先假定温度锋面推进距离ΔL,并计算出相应的tn+1时刻连续流区温度分布,然后计算出tn+1时刻气动加热净热流,并近似取Δt时间内的热管连续流区的加热量为tn时刻和tn+1时刻气动加热的平均值,即:
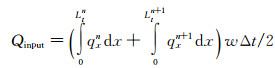
|
(12) |
其中,w为热管壳体截面周长。
使用计算得到的两个时刻的连续流区温度分布可获得轴向长度“0~Ltn”段和“Ltn~Ltn+1”段温升所需热量Q1和Q2(如图 1所示),两者之和即为当前时刻连续流区温升所需总热量Qneed。
根据Qinput和Qneed大小关系,通过迭代计算不断调整ΔL的值使得Qinput和Qneed相等,即可求得当前时间步温度锋面的推进距离。
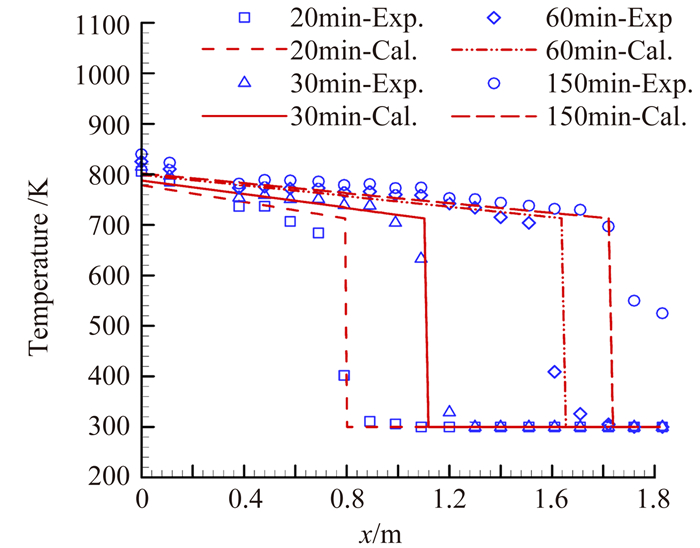
3 试验验证与计算分析 3.1 圆柱热管启动试验验证采用文献[14]中给出的均匀受热圆柱热管启动试验结果对计算方法进行验证,试验热管蒸发段加热功率289.6W,壳体材料为不锈钢,热管蒸发段、绝热段、冷凝段长度分别为0.375m、0.745m和0.91m,钠填充量为92.04g。图 4为热管启动过程不同时刻温度沿轴向分布计算结果与试验结果的比较。
|
| 图 4 计算结果与文献试验数据比较 Fig. 4 Calculated temperatures compared with experimental data |
可以看出,计算得到的前端点温度略低于试验值,而温度锋面位置和温度分布均与试验测量结果符合很好,表明所述计算方法能够较好的模拟高温热管启动过程真实温度分布和“温度锋面”推进进程。
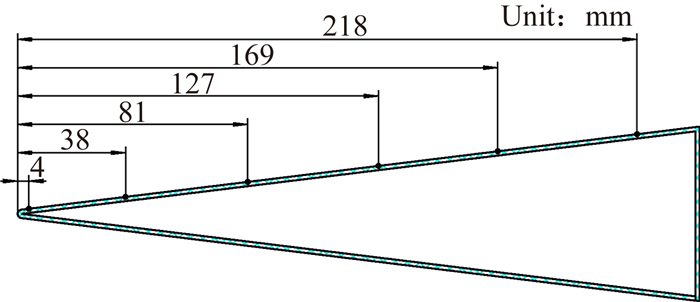
3.2 尖前缘一体化热管启动试验验证中国航天空气动力技术研究院采用石英灯辐射加热设备完成了典型尖前缘一体化高温钠热管的启动试验。试验热管为尖楔外形,楔面扩张半角7°,热管总长240mm,钠填充量约20.0g,沿热管轴向中心部位共布置6个温度传感器(从左至右依次编号1~6)用于测量热管表面温度,热管外形及测点位置分布如图 5所示。
|
| 图 5 热管外形及温度测点分布 Fig. 5 Typical configuration and temperature measuring position of heat pipe |
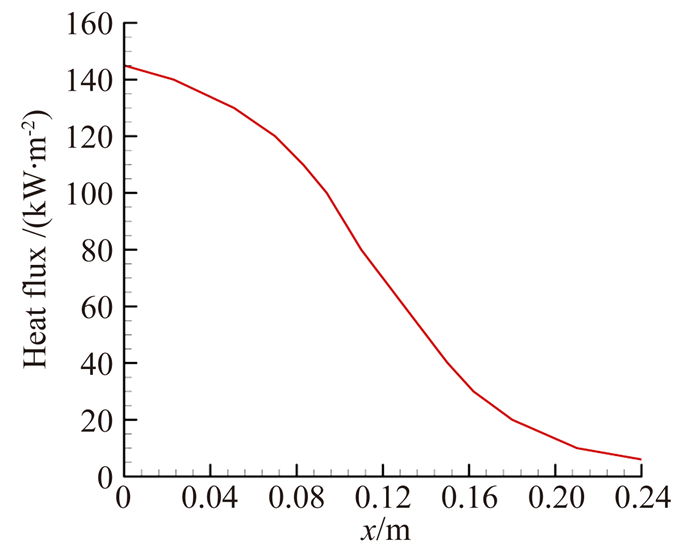
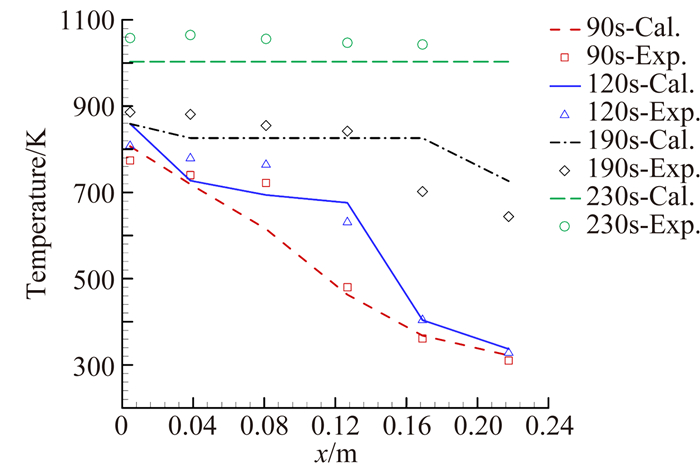
试验结果表明,热管启动顺利,且在220s左右接近达到等温体,前后端温差小于30℃。根据试验条件换算表面辐射热流作为输入参数(图 6为最终稳定辐射热流),计算热管启动时间(形成完全蒸汽流动)为158s,形成等温体时间为209s。图 7为各测点温度计算结果与试验数据的比较。
|
| 图 6 石英灯加热稳定辐射热流 Fig. 6 Radiative heat flux the of quartz lamp heater |
|
| 图 7 计算结果与辐射加热启动试验数据比较 Fig. 7 Calculated temperatures compared with radiation heating experimental data |
可以看出,计算得到各测点温度与试验数据基本吻合。受试验测试环境与测试方法影响,部分时刻测点(测点3,90s;测点5,190s)计算结果与试验数据偏差较为明显(230s左右测点6脱落,无温度数据)。此外,由于石英灯辐射面较大,热管蒸发冷凝段均承受了一定程度的辐射加热,因此热管启动的“温度锋面”特征不是特别明显。
总的来看,目前的计算方法已能满足尖前缘一体化高温热管启动性能的工程分析需求,对尖前缘高温热管设计启动性能评估具有重要意义。
3.3 尖前缘一体化热管启动性能影响因素分析在实际工程应用条件下,高温热管的迅速启动对于飞行器前缘驻点部位的防热非常重要,过长的启动时间可能导致前缘驻点部位因高温发生破坏。为了分析尖前缘一体化热管启动特性的影响因素,针对某尖前缘一体化高温热管结构在如图 2(a)所示气动加热环境下的启动性能进行计算分析。
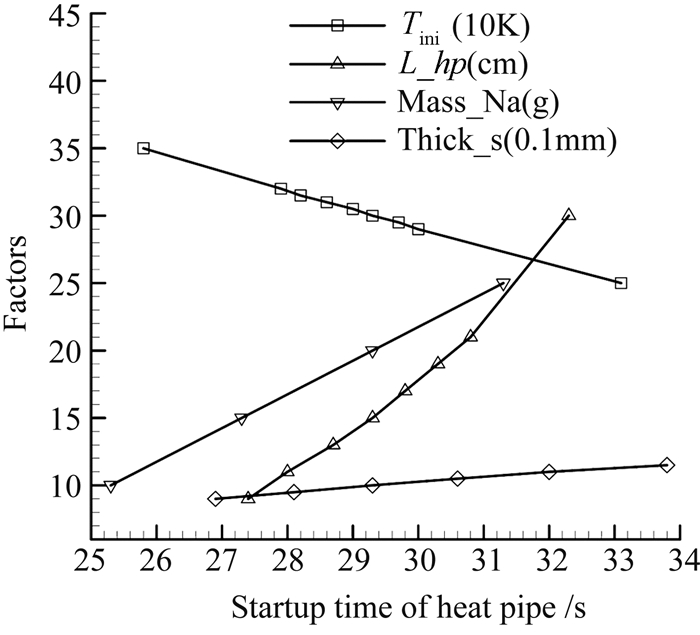
图 8为计算得到的热管总长L_hp、壳体厚度Thick_s、钠工质充装质量Mass_Na以及热管初始温度Tini对热管启动时间的影响规律,其中横坐标为热管启动时间。
|
| 图 8 热管启动时间影响因素 Fig. 8 Influencing factors for heat pipe startup |
可以看出,减小热管总长、减小壳体厚度、减小工质充装量或者提高初始使用温度均有利于热管的快速启动。因此在尖前缘高温热管的设计过程中,根据热管的实际使用环境及工程设计需求,在结构尺寸、强度及防热性能等设计要素均满足要求的前提下,结合本文建立的热管启动性能工程计算方法,通过优化热管结构参数或者对热管进行预热等方法可有效缩短热管的启动时间。
4 结论本文建立了一种适合用于飞行器尖前缘不规则外形一体化高温热管在气动加热环境下启动性能的工程计算方法;使用试验数据对计算方法进行了验证。通过研究表明,尖前缘一体化高温热管启动后等温性能良好,计算方法能够较好模拟尖前缘不规则外形高温热管启动过程,通过调整热管结构参数或使用环境可进一步缩短热管启动时间。
但需指出的是,飞行器尖前缘高温热管在气动加热环境下的启动过程是一个多种传热传质因素相互耦合的复杂过程。本文建立的工程计算方法适用于对飞行器尖前缘整体式热管启动性能的快速预测和前期设计评估,但未针对高温热管的传热极限[15]和内部液态工质的流动过程进行深入分析,这些因素对尖前缘高温热管启动性能可能产生的影响还有待进一步研究确认。
| [1] |
Li Feng, Ai Bangcheng, Jiang Guiqing. A new thermal protection technology based on heat-balance isothermal mechanism[J].
Journal of Astronautics, 2013, 34(12):1644–1650.
(in Chinese) 李锋, 艾邦成, 姜贵庆. 一种热平衡等温机制的新型热防护及相关技术[J]. 宇航学报, 2013, 34(12) : 1644–1650. |
| [2] |
Han Haitao, Deng Daiying, Chen Siyuan, et al. Design and Structural analysis of sharp leading edge integrated with heat pipe[J].
Journal of Mechanical Strength, 2013, 35(1):048–052.
(in Chinese) 韩海涛, 邓代英, 陈思员, 等. 尖前缘一体化高温热管结构设计与分析[J]. 机械强度, 2013, 35(1) : 048–052. |
| [3] |
Jiang Guiqing, Ai Bangcheng, Yu Jijun. Application of high temperature heat pipe in leading thermal protections[C]//Proceedings of 11th China Heat Pipe Conference. Beijing:Beijing Science and Technology Press, 2008:74-80. (in Chinese) 姜贵庆, 艾邦成, 俞继军, 等.高温热管在疏导热防护技术中的应用[C]//第十一届全国热管会议论文集, 北京:北京科学技术出版社, 2008:72-78. |
| [4] | Ponnappan R, Boehman L I, Mahefkey E T. Diffusion controlled startup of a gas loaded liquid metal heat pipe. AIAA-89-1707[R]. Reston:AIAA, 1989. |
| [5] | Chang W S. Startup of the liquid-metal heat pipe in aerodynamic heating environments[R]. ADA 307203. |
| [6] | Glass D E. Closed form equations for the preliminary design of a heat-pipe-cooled leading edge[R]. NASA/CR-1998-208962. |
| [7] | Glass D E, Camarda C J, Merrigan M A, et al.Fabrication and testing of a leading-edge-shaped heat pipe. AIAA-99-4866[R]. Reston:AIAA, 1999. |
| [8] | Cao Y, Faghri A. A numerical analysis of high-temperature heat pipe startup from the frozen state[J]. Journal of heat transfer, 1993, 115:247–254. DOI:10.1115/1.2910657 |
| [9] | Cao Y, Faghri A. Closed-form analytical solutions of high-temperature heat pipe and frozen startup limitation[J]. Journal of Heat Transfer, 1992, 114:1028–1035. DOI:10.1115/1.2911873 |
| [10] |
Qu Wei, Wang Huanguang. Compatibility and heat tansfer of high and super high temperature heat pipes[J].
CIESC Journal, 2011, 62(S1):77–81.
(in Chinese) 曲伟, 王焕光. 高温及超高温热管的相容性和传热性能[J]. 化工学报, 2011, 62(S1) : 77–81. |
| [11] |
Qu Wei, Wang Huanguang, Duan Yanjun. Startup characteristics and heat transfer limits of high and super high temperature heat pipes[J].
Journal of Engineering Thermophysics, 2011, 32(8):1345–1348.
(in Chinese) 曲伟, 王焕光, 段彦军. 高温及超高温热管的启动特性和传热极限[J]. 工程热物理学报, 2011, 32(8) : 1345–1348. |
| [12] |
Huang Shengyun, Guo Hang, Ye Fang. Advances in study of start-up performance of heat pipes[J].
Modern Chemical Industry, 2009, 29(7):27–30.
(in Chinese) 黄生云, 郭航, 叶芳. 热管启动性能研究进展[J]. 现代化工, 2009, 29(7) : 27–30. |
| [13] |
Jiao Yonggang, Xia Guodong, Zhou Mingzheng, et al. Starting characteristics of sodium heat pipe in metrology based on "flat-front" startup model[J].
CIESC Journal, 2012, 63(3):781–787.
(in Chinese) 焦永刚, 夏国栋, 周明正, 等. 基于"平面前锋"启动模型的计量用钠热管启动特性[J]. 化工学报, 2012, 63(3) : 781–787. |
| [14] | Faghri A. Continuum transient and frozen startup behavior of conventional and gas-loaded heat pipes[R]. ADA 284297, Wright State Univ. Dayton. OH Dept. of Mechanical and Materials Engineering, 1992. |
| [15] | 庄俊, 张红. 热管技术及其工程应用[M]. 北京: 化学工业出版社, 2000 . |



