大迎角零侧滑条件下,旋成体布局以及大后掠尖缘三角翼布局出现的非对称流动现象受到国内外学者长达数十年的关注和研究[1-5]。但是由于大迎角非对称性涉及流动问题描述的完备性、流动稳定性产生、发生机制、流体运动的分岔混沌现象等复杂的流动基础性问题,至今对于非对称流动产生机制,以及由非对称而引发的一系列复杂现象,尚无一致的认识,但是学术界在大迎角非对称流动研究中所做的大量研究工作,特别是围绕抑制、消除侧向力和偏航力矩问题开展的大量研究工作对改善飞行器在大迎角的性能、提高机动性和敏捷性具有很好的工程应用价值。
在进行带“X”型布局小展弦比梯形尾舵的旋成体导弹的风洞测力试验中,我们发现在小迎角、零侧滑、跨声速来流条件下,当尾舵俯仰舵偏角δz=30°时,全弹出现了较大的侧向力及滚转力矩,此横向量与滚转舵偏角5°时产生的横向量量值相当,影响了全弹的气动特性,尤其是舵面的操纵特性。随后,我们基于一系列的部件组拆测力试验最终确定,此横向量的产生是呈开口布局一对尾舵的翼尖涡非对称性引起的。
为进一步对非对称流场细节进行观测,我们基于已获得的试验数据及流场观测结果,开展了该问题的数值模拟研究。本文着重分析了非对称流场随舵偏角的变化,开展了临界舵偏角下非对称翼尖涡的发展及对舵面压力分布的影响研究,并对该非对称流动现象产生的机理进行了分析。基于以上分析结果,在保持舵面效率不降低的情况下开展了消除非对称流动现象的方法研究。
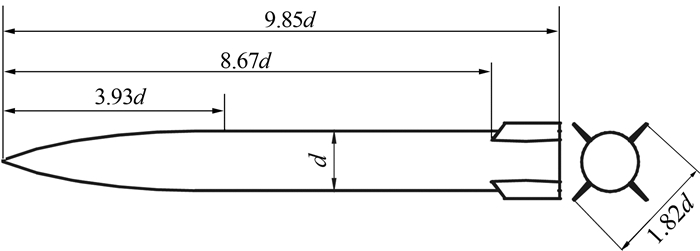
1 风洞试验现象描述 1.1 试验模型图 1给出了本文研究模型的外形示意图。模型头部为尖拱形,长细比为3.93,弹身为圆柱形,直径为d,长细比为5.92,尾舵为展弦比0.35的梯形舵,前缘后掠角为30°,尾舵前缘距模型头部8.67d,尾舵根弦长为1.1d,呈“X”型布局安装于弹身尾部。
|
| 图 1 模型外形图 Fig. 1 Basic schematic of the model |
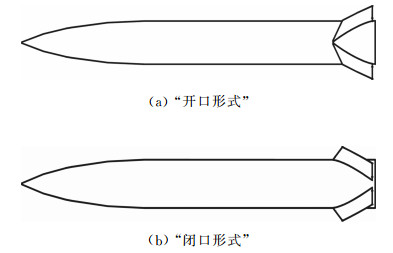
图 2给出了俯仰舵偏角30°时,尾舵布局形式俯视图和上视图。从图中可以看出相对来流来说背风面和迎风面的尾舵安装形式有明显的差异,安装在弹身背风面的两片尾舵沿气流方向呈打开形式定义为“开口形式”,而迎风面两片尾舵则呈“闭口形式”。
|
| 图 2 δz=30°尾舵偏转形式示意图 Fig. 2 Schematic of model (δz=30°) |
1.2 试验结果与分析
六分量天平测力试验在0.6m×0.6m跨、超声速风洞中完成。测力试验马赫数范围为0.4~1.2,迎角范围为-4°~12°,基于弹身直径的雷诺数范围为Red=4.13×105~1.03×106/m。参考面积为弹身横截面积,力矩系数参考长度为全弹长,参考点为模型头部顶点。
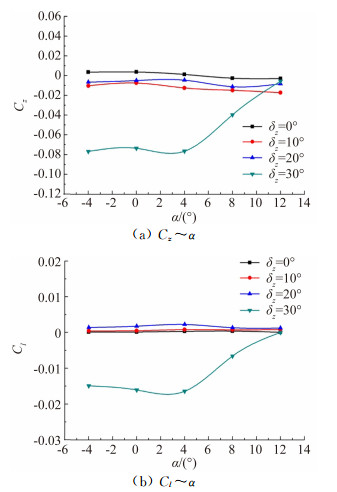
图 3所示为Ma=0.95、β=0°时,不同俯仰舵偏角下,全弹侧向力和滚转力矩系数随迎角的变化。从图中可以看出,在小迎角范围,当俯仰舵偏角达到30°时,全弹产生了较大的侧向力和滚转力矩,尤其是所产生的滚转力矩量值与滚转舵偏角5°时产生的滚转力矩相当,对全弹控制特性提出了挑战。针对该现象,项目组首先通过不同舵面位置进行互换,排除了模型加工误差的因素,另外在另一座风洞中进行了校核试验,排除了风洞流场的因素。另外,大量研究结果已经表明,在跨声速小迎角条件下,旋成体弹身不会产生非对称现象,因此初步断定非对称流动现象是由大偏度下尾舵引起的。而由图 2所示在俯仰舵偏角同为30°时,迎风面(下表面)、背风面(上表面)尾舵的布局形式是不同的,为进一步研究横向量是来源于上表面两片尾舵还是下表面两片尾舵,将上、下表面两片尾舵的俯仰舵偏角分别设为0°和30°,则此时有两种舵偏组合状态,即上表面尾舵舵偏角0°、下表面30°(标记为:T_δz=0,B_δz=30)和上表面尾舵舵偏角30°、下表面0°(标记为:T_δz=30,B_δz=0)。对这两种舵偏组合状态在α=0°,β=0°,Ma=0.4~1.2分别进行了测力试验。
|
| 图 3 Ma=0.95、β=0°时,不同俯仰舵偏角下,全弹侧向力和滚转力矩系数随迎角的变化 Fig. 3 Side force and rolling moment coefficients at Ma=0.95, β=0° |
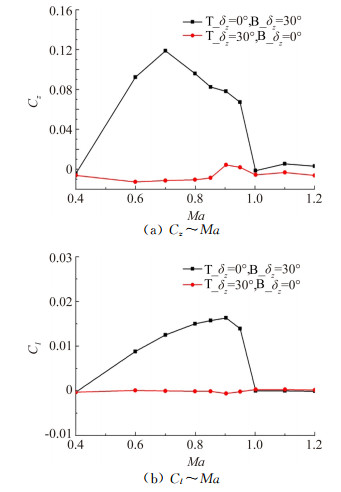
从图 4两种舵偏组合状态全弹侧向力和滚转力矩系数随马赫数的变化可以明显看出俯仰舵偏角30°时全弹横向量是由上面两片舵产生的。即当尾舵俯仰舵偏角达到30°时,呈开口形式的两片尾舵会产生非对称流动。
|
| 图 4 α=0°、β=0°时,俯仰舵偏角为30°时全弹侧向力和滚转力矩系数随马赫数的变化 Fig. 4 Side force and rolling moment coefficients of the two models at α=0°, β=0° |
为进一步从流场结构和流态上验证该测力试验结果,进行了粒子图像测速(PIV)试验。测试截面位于模型底部后方0.1d处。
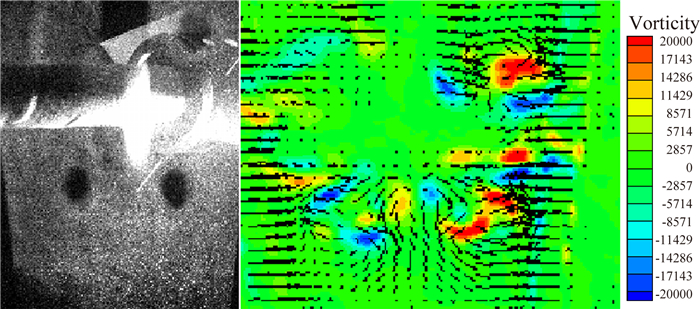
图 5为α=β=0°、δz=30°、Ma=0.95时PIV试验原始图像以及均速度场和涡量场。图中“黑洞”为模型尾舵产生的流向涡涡核位置。可以看出,与测力试验结果一致,“闭口形式”两涡核形态清晰,对称性较好,而“开口形式”呈现明显的非对称性。
|
| 图 5 PIV试验结果(Ma=0.95) Fig. 5 Results of PIV test(Ma=0.95) |
2 数值模拟方法及有效性检验
由于试验对流场细节观测的手段有限,以及试验过程中改变舵面参数和舵偏角较为困难,基于已有试验结果,我们借助数值模拟方法对非对称流场细节、舵面压力分布、不同舵偏角的影响、舵面形状影响等进行了细致的分析。
2.1 数值模拟方法控制方程采用三维雷诺平均N-S方程,在计算坐标系下可写为:

|
(1) |
基于SST湍流模式的DES方法通过对湍动能耗散项的改造,实现RANS模式和LES模式的切换。控制方程采用有限体积法进行离散,时间项采用双时间步法(Dual Time Step Method)进行离散求解以获取二阶精度。对流项及扩散项均采用二阶中心差分格式进行处理,为了抑制数值震荡加入四阶人工粘性项,具体参考文献[6-8]。无量纲时间步长取0.01,采用结构网格,远场边界距离物面均在15倍弹身长度以上,物面采用无滑移绝热壁面条件,远场边界采用无反射远场边界条件,全弹总网格量450万。计算采用时间精确求解,每个状态计算5000物理时间步,气动力系数基本在3000步趋于稳定。
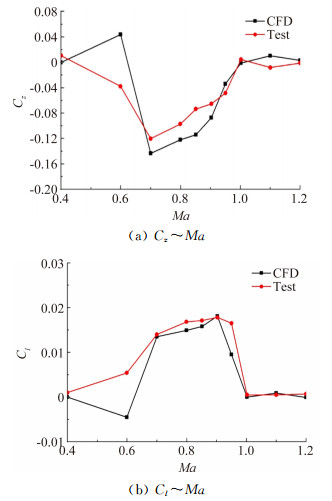
2.2 计算结果与试验结果的对比为验证所采用数值模拟方法和网格划分的有效性,首先在α=0°、Ma=0.4~1.2范围对全弹的横向量计算结果与试验值进行了对比,如图 6所示。从图中可以看出,与试验在α=0°、Ma=0.6~0.95范围全弹产生了较大的侧向力和滚转力矩的结果一致,计算结果也捕捉到了此非对称现象,并且从侧向力和滚转力矩系数量值来看,计算结果与试验值取得了较好的一致性。Ma=0.6时,计算与试验所获得的非对称现象所产生的横向量的方向是相反的,反映了此非对称现象产生的横向量的方向是不定的。总体来说,所采用的数值模拟方法能够准确捕捉本文所研究的非对称现象,基于此方法开展流动机理和主要影响参数研究是可行的。
|
| 图 6 全弹的横向量计算结果与试验值对比 Fig. 6 Comparison of the experimental data with CFD results |
3 计算结果分析 3.1 舵偏角的影响研究
由于测力试验时,俯仰舵偏角有限,仅对0°、10°、20°和30°舵偏角的全弹气动特性进行了风洞测力试验,测力试验和计算结果表明在Ma=0.6~0.95范围,舵偏角30°时呈开口布局的两片尾舵由于翼尖涡的非对称性,会使全弹产生较大的横向量,为寻求此非对称现象产生的临界俯仰舵偏角,分析临界状态下的流场特性,基于数值模拟方法在俯仰舵偏角20°~30°范围进行了舵偏角影响的计算分析。
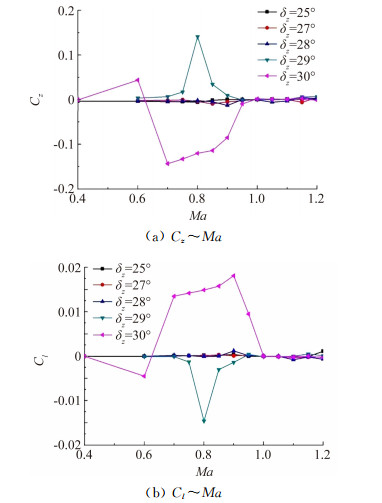
图 7所示为不同俯仰舵偏角下,全弹横向量随马赫数的变化,从图中可以看出俯仰舵偏角小于27°时,全弹横向量基本为0,即没有非对称现象产生,当舵偏角达到28°时,在马赫数0.9时开始有小的横向量产生,当俯仰舵偏角进一步增大到29°时,有横向量产生的马赫数区域增大,且横向量的量值增加。不难看出随着俯仰舵偏角的增加,呈开口布局一对尾舵的前缘距离逐渐减小,非对称现象逐渐增强。
|
| 图 7 不同俯仰舵偏角下,全弹横向量随马赫数的变化 Fig. 7 Side force and rolling moment coefficients of different angles of pitch |
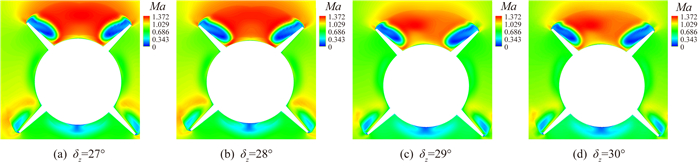
图 8和图 9为不同俯仰舵偏角下呈开口布局尾舵物面压力系数和典型剖面马赫数分布。与图 7全弹横向量随马赫数的变化结果一致,图 8和图 9呈现了流场的不对称性随俯仰舵偏角的发展,可以看出俯仰舵偏角27°时,呈开口布局的一对尾舵物面压力分布是对称的,俯仰舵偏角增大到28°时,左、右尾舵的翼尖涡开始呈现非对称性,右侧尾舵的翼尖涡强度略强,使得右侧尾舵物面的低压区范围较左侧尾舵略大,俯仰舵偏角增大到29°时,此非对称现象逐渐增强,左、右尾舵的物面压力差异增大,并且随着俯仰舵偏角的进一步增大此差异也进一步增加,俯仰舵偏角30°时,右侧尾舵的翼尖涡消失,右侧尾舵附近有较大面积的死水区,使得右侧尾舵物面压力系数较大。

|
| 图 8 Ma=0.9,呈开口布局尾舵物面压力系数 Fig. 8 Pressure coefficient distributions of the fin surface at Ma=0.9 |
|
| 图 9 x/d=9.22剖面马赫数云图随舵偏角的变化 Fig. 9 Mach number contours of typical section under different angles of pitch at x/d=9.22 |
3.2 非对称流动形成的机理分析
尽管自1952年Cooper等在试验中发现旋成体在大迎角零侧滑下出现非对称流动现象已数十年,然而由于其流动现象的影响因素的复杂性,非对称旋涡流型的形成机理至今还未得到很好的理解和一致的看法[9-10],但其中一个观点对解释本文所阐述的非对称现象具有一定的指导意义,即旋成体的一对背涡由于十分临近而引起的旋涡不稳定性形成非对称旋涡流型[11-13]。大量试验研究结果表明旋成体前体长细比(l/d)f对起始迎角和最大非对称侧向力具有决定性的作用,当(l/d)f越大(即旋成体头部半顶角越小),在旋成体头部两侧分离而形成的一对旋涡位置十分临近,使这一对反向旋转的旋涡变得不稳定,引起的非对称侧向力的起始迎角越小[14-15]。大量试验结果也表明这样的假设同样也可以用来解释大后掠尖缘三角翼的非对称流动现象,当三角翼后掠角大于75°时[16],由于翼面上方的一对前缘涡相距过近而互相干扰结果形成前缘涡的非对称分布,并且随着后掠角的增大,前缘涡非对称现象的起始迎角迅速降低。
通过上文变舵偏角的测力试验结果表明,当舵偏角为30°时,呈开口布局的一对尾舵出现了非对称流动现象,而10°和20°舵偏角下无非对称流动现象发生,这个现象也表明当舵偏角达到一定角度时,呈开口布局的一对尾舵前缘相距太近,其翼尖涡相互干扰形成了非对称分布,试验模型舵偏角30°时,呈开口布局的一对尾舵的翼前缘距离l仅为3.1mm。
为了验证此设想,我们进行了如下工作:
1)保持俯仰舵偏角和舵面形状不变,将呈开口布局的一对尾舵的相对距离增大。
尾舵按相向方向分别平移l和2l,此时翼尖的距离分别变为3l和5l,弹体的半径略有改变,分别为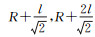
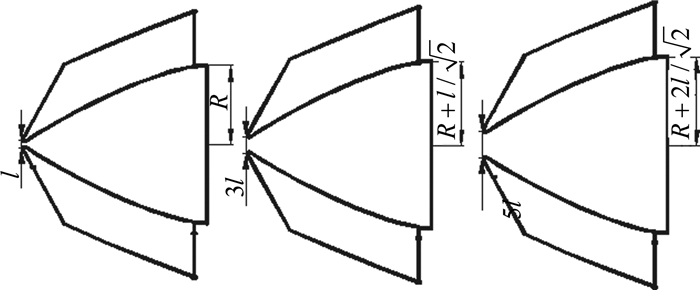
|
| 图 10 翼尖相对距离增大布局 Fig. 10 sketches of increasing the relative distance of the leeward pair of fins |
图 11给出了翼前缘距离分别为l(原始外形)、3l、5l时,全弹侧向力和滚转力矩系数的对比。从图中可以看出,翼前缘距离为3l时,全弹仅在马赫数0.85至0.95范围有非对称现象产生,且横向量与原始外形相比有所降低,当翼前缘距离进一步增加到5l时,非对称现象消失,进一步说明此非对称现象产生的机理与大迎角时旋成体布局以及三角翼布局的非对称现象产生的机理有共通之处。
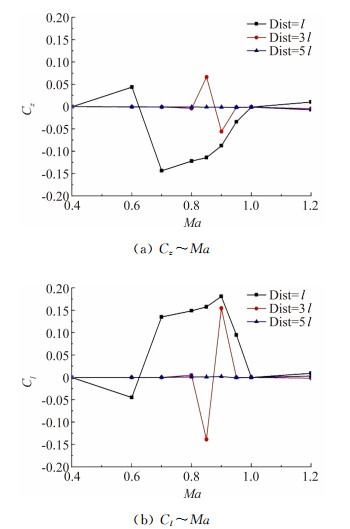
|
| 图 11 翼尖相对距离增大对横向量的影响 Fig. 11 Effects on side force and rolling moment coefficients of the relative distance |
2)保持弹身尺寸不变,以尾舵转心为参考点将尾舵进行缩比。
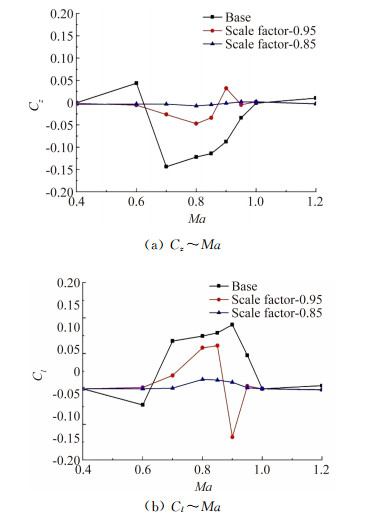
图 12所示为保持弹身尺寸不变、以尾舵转心为参考点将尾舵缩比前后对比示意图。分别将尾舵缩比为原始尺寸的95%和85%,此时翼尖的距离分别变为3.5l和4.6l。图 13给出了尾舵缩比前后全弹横向量的对比,可以看出随着尾舵尺寸的减小,尾舵翼尖相对距离逐渐增大,全弹横向量逐渐减小,与保持俯仰舵偏角和舵面形状不变,将呈开口布局的一对尾舵的相对距离增大的效果一致。
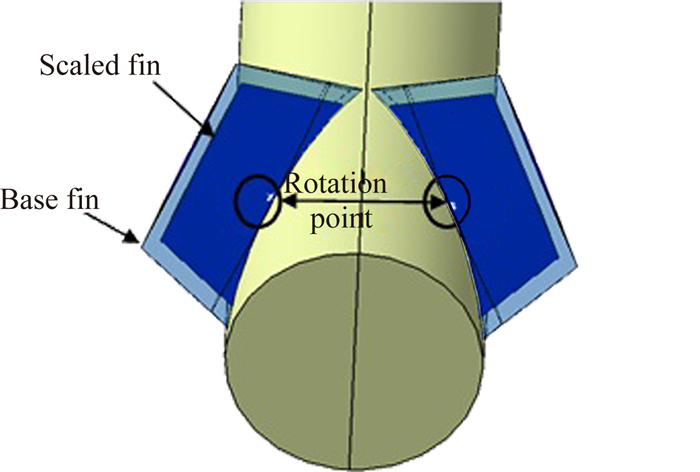
|
| 图 12 尾舵缩小布局示意图 Fig. 12 Sketch of scaling the leeward pair of fins |
|
| 图 13 尾舵缩小对气动特性的影响 Fig. 13 Comparison of the side force and rolling moment coefficients of the scaled fins with the original one |
3.3 消除非对称流动的方法研究
通过上文的研究可以看出,尾舵前缘距离是形成非对称流动的主要影响因素,因此降低尾舵前缘距离是消除非对称流动现象的突破点,然而与此同时又不能降低尾舵的舵面效率,我们尝试了以下两种布局方案:
1)前缘局部切角。如图 14所示,保持尾舵后掠角不变,将尾舵翼前缘局部进行切角,切除的小三角的边长为5l,以Cut进行标记。

|
| 图 14 前缘局部切角 Fig. 14 Sketch of cutting off the local area around the leading edge |
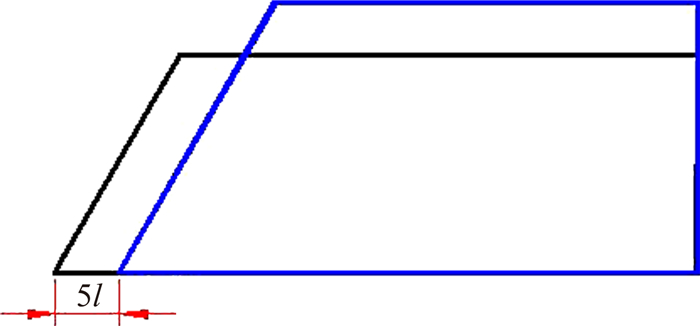
2)降低尾舵根弦长。如图 15所示,仍以5l作为特征长度,将翼根长度减小5l,同时为保持尾舵面积不变,将尾舵展长适当增大,以Short RC进行标记。
|
| 图 15 翼根长度变短 Fig. 15 Sketch of reducing the root chord length while increasing the span length |
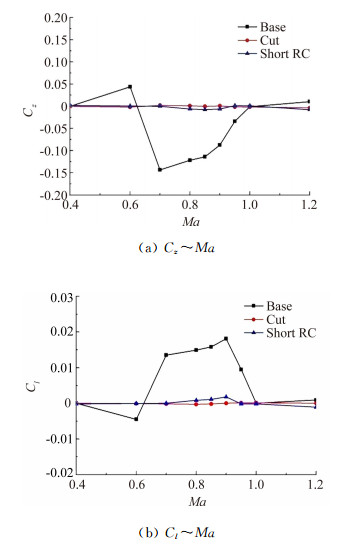
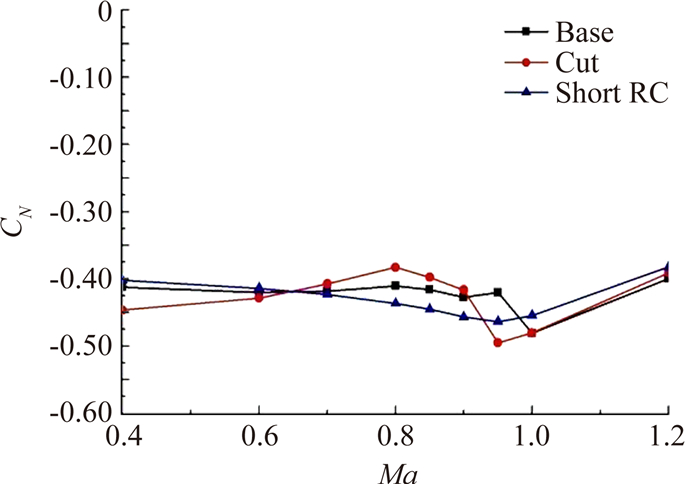
同样情况下,对以上两种布局的气动特性进行了数值模拟,从图 16所示两种尾舵布局条件下全弹侧向力和滚转力矩系数随马赫数的变化与基本布局的对比,可以看出以5l作为特征长度的前缘局部切角以及翼根长度缩短布局的横向量基本消失,达到了消除非对称流动的目标。另外从两种尾舵布局法向力系数与基本尾舵布局法向力系数的对比(图 17)中可以看出,两种尾舵布局法向力系数与基本尾舵的法向力系数相当,舵面效率没有损失,可以直接为工程所用。
|
| 图 16 不同布局对气动特性的影响 Fig. 16 Comparisons of the side force and rolling moment coefficients of different fins |
|
| 图 17 不同布局尾舵法向力的系数对比 Fig. 17 Comparisons of the normal force coefficients of different fins |
4 结论
本文通过数值模拟方法对小展弦比尾舵大偏度下产生的非对称流动现象进行了分析,得出如下结论:
1)随着舵偏角的增加,呈开口布局的一对尾舵的翼尖涡距离逐渐减小,翼尖涡相互干扰,翼尖涡强度由弱的不对称性逐渐发展,直到其中一侧翼尖涡消失;
2)采用尾舵前缘局部切角和适当降低尾舵翼根长度的形式,降低尾舵前缘的相对距离可以有效减弱和消除此非对称现象, 同时对尾舵的舵面效率影响不大。
本文的研究结果对类似布局设计有一定的参考价值。
| [1] | Bernhardt J E, Williams D R. Close-loop control of forebody flow asymmetry[J]. Journal of Aircraft, 2000, 37(3):491–498. DOI:10.2514/2.2624 |
| [2] | Ericsson L E, Reding J P. Aerodynamic effects of asymmetric vortex shedding from slender bodies. AIAA-85-1797[R]. Reston:AIAA, 1985. |
| [3] | Telionis D P, Zeiger M D, Vlachos P P. Unsteady separated flow over 3-D slender bodies, AIAA 99-3693[R]. Reston:AIAA, 1999. |
| [4] | Vadyak J, Schuster D M. Navier-Stokes simulation of burst vortex flowfields for fighter aircraft at high incidence[J]. Journal of Aircraft, 1991, 28(10):638–645. DOI:10.2514/3.46076 |
| [5] |
Zhou Naichun, Ye Zhengyin, Hu Handong. Asymmetric vortex structure ofslender revolution at high angles of attack[J].
Acta Aerodynamica Sinica, 2004, 22(4):486–493.
(in Chinese) 周乃春, 叶正寅, 胡汉东, 等. 细长尖头旋成体大迎角非对称涡系结构[J]. 空气动力学学报, 2004, 22(4) : 486–493. |
| [6] | Spalart P R, Deck S, Shur M L, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[M]. Liu C, Liu Z, eds. Advances in DNS/LES. Columbus, OH:Greyden Press. 1997:137-47. |
| [7] | Travin A, Shur M, Strelets M, et al. Physical and numerical upgrades in the Detached-Eddy Simulation of complex turbulent flows[J]. Fluid Mechanics and its Applications, 2002(65):239–254. |
| [8] | Haase W, Braza M, Revell A. DESider-A European effort on hybrid RANS-LES modelling:Results of the European-Union Funded Project, 2004-2007[M]. Springer-Verlag Berlin Heidelberg Press: 2009 . |
| [9] |
Gu Yunsong, Ming Xiao. Investigation of flow field characteristics on a slender body at high angle of attack[J].
Journal of Experiments in Fluid Mechanics, 2005, 19(2):1–6.
(in Chinese) 顾蕴松, 明晓. 大迎角细长体非对称空间流场特性的试验研究[J]. 实验流体力学, 2005, 19(2) : 1–6. |
| [10] | Hunt B L, Northrop C, Hawthorne C A. Asymmetric vortex forces and wakes on slender bodies. AIAA-82-1336[R]. Reston:AIAA, 1982. |
| [11] |
He Zhong, Fan Zhaolin, Wang Yuanjing. Analysis of compressibility effect tests on ogive slender body at high angles[WX)] [WX(4.5mm, 75.5mm] of attack[J].
Acta Aerodynamica Sinica, 2010, 28(3):332–336.
(in Chinese) 贺中, 范召林, 王元靖. 细长体大迎角压缩性效应试验分析[J]. 空气动力学学报, 2010, 28(3) : 332–336. |
| [12] | Skow A M, Erickson G E. Modern fighter aircraft design for high angle of attack maneuvering[R]. AGARD LS-121, 1982. |
| [13] | Polhamus E C. Prediction of vortex lift characteristics by a leading-edge suction analogy[J]. J. of Aircraft, 1971, 8(4):193–199. DOI:10.2514/3.44254 |
| [14] | Keener E R, Chapman G T. Similarity in vortex asymmetries over slender bodies and wings[J]. AIAA J., 1977, 15(9):1370–1372. DOI:10.2514/3.60795 |
| [15] | Woolard H W. Similarity relation for vortex-asymmetry onset on slender pointed forebodies[J]. AIAA J., 1982, 20(4):559–561. DOI:10.2514/3.7929 |
| [16] | Roos F W, Kegelman J T. An experimental investigation of sweep-angle influence on delta-wing flows. AIAA-90-0383[R]. Reston:AIAA, 1990. |



