2. 中国空气动力学研究与发展中心, 四川 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
近年来,随着科研工作者对计算精度的要求越来越高,高精度数值方法受到越来越多的关注。在众多的高精度方法中,间断有限元方法由于精度高且插值模板小,易于实现网格和阶数自适应,以及并行计算效率高等优点,在计算流体力学、计算声学、计算电磁学领域都得到了广泛的关注和发展[1]。
间断有限元方法发展于20世纪70年代,由reed和hill在其解决中子运输方程的论文中提出。20世纪80年代后期和90年代,cockburn和shu等人[2-5]发展了runge-kutta discontinuous galerkin(rkdg)方法,求解了非线性一维守恒律方程和方程组、高维守恒律方程和方程组,并给出了部分收敛性理论证明后,该方法才引起了人们注意,并开始逐渐应用于计算流体力学领域。目前dg方法不仅应用于双曲守恒律方程,还被广泛应用于求解椭圆型方程、对流扩散方程、kdv方程、maxwell方程、可压缩navier-stokes(n-s)方程等[6-18]。bassi等[6-8]采用dg方法结合k-ω两方程湍流模型求解了雷诺平均n-s方程,luo等[10-12]研究了基于加权本质无振荡(weighted essentially non-oscillatory, weno)的重构间断有限元方法,邱建贤等[13]针对weno限制器在dg方法中的应用展开大量研究;张来平等[14]发展了静动态混合重构的dg/fv混合格式。
间断Galerkin(DG)方法通过提高单元阶数来提高精度,可以在相对稀疏的网格单元上得到较高精度的数值解。但较稀疏的物面单元使得边界表述不够准确,从而引入额外的数值熵增[6],使得计算结果不准确。为了对边界进行高阶表述,文献[6, 15]采用高阶等参单元对二维和三维Euler方程进行了数值求解,文献[16-17]则借助于CAD工具对全场计算单元进行了高阶表述。为了减少计算代价,文献[18-21]采用一种边界弯曲方法在较稀疏的二维网格上得到了高精度的数值解。
本文作为二维DG方法研究[22-23]的拓展,将DG方法用于求解三维可压缩气动方程组。与以往工作不同点在于:将边界网格弯曲方法拓展到三维六面体网格单元,根据四边形面网格单元信息构造出相应的弯曲边界信息,更准确地表述了真实壁面特征,从而在相对稀疏的网格上求解气动方程组。为了提高DG方法的计算效率,文中采用了隐式计算方法。此外,文中发展的间断有限元方法理论上可以拓展到任意高阶精度。
1 控制方程守恒形式的Navier-Stokes方程可以表示为
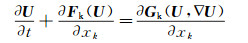
|
(1) |
其中守恒变量 U、对流通量F、黏性通量G可用下面的张量形式来表示:

|
(2) |
其中ρ、p、e、h分别是流体密度、压强、单位总能和单位总焓。ui=(u, v, w)是三维笛卡尔坐标系下的速度分量,σij是黏性应力分量,qj是热通量分量。若不考虑黏性通量G,则方程(1)退化为守恒形式的欧拉方程[12]。
2 数值方法 2.1 空间离散令Ω表示对计算区域的一个剖分,e为剖分单元体,文中为六面体单元,əΩe表示单元e的边界,n e表示单元边界əΩe的外法矢。在方程(1)两边同乘测试函数ω,在计算域积分后可得:

|
(3) |
其中, F(U, ▽U)是对流通量F(U)和黏性通量G(U, ▽ U)的和。定义分片多项式构成的有限元空间:
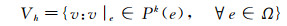
|
(4) |
其中Pk(e)表示单元e上定义的至多k次多项式。求解方程(1)的半离散间断有限元方法即为:求解U h∈Vh,使得对于任意单元和任意测试函数ωh∈Vh,有:
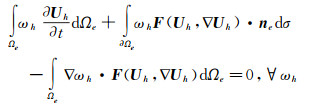
|
(5) |
方程(5)中存在二阶偏导数项,这里采用混合方法进行求解,将变量梯度看作额外变量,引入辅助变量 Θ=▽ U,得到如下方程组:
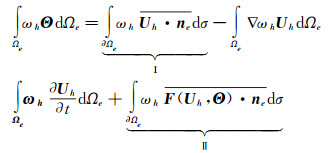
|
(6) |
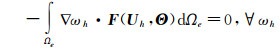
|
(7) |
采用the Second Bassi and Rebay Scheme(BR2格式)[8],数值通量I中取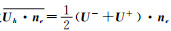

|
(8) |
从式(8)可以看出,辅助变量可以看成单元梯度解和修正量 R 的和:
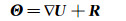
|
(9) |

|
(10) |
面的梯度修正量 r e可以表述为:
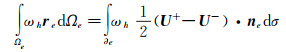
|
(11) |
方程右边表示在单元某个面上进行面积分,可以看出;
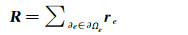
|
(12) |
采用以上方法求出方程(6)中的辅助变量,方程(7)中未知量仅剩下单元变量 U 为未知量。数值通量II中通量函数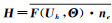
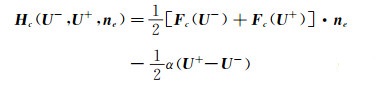
|
(13) |
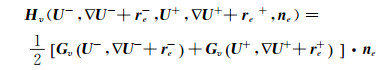
|
(14) |
式(7)的半离散系统可以写成常微分方程组:

|
(15) |
M 是块对角矩阵,R(u)是总残值, u是待求未知变量。采用牛顿方法进行线化,得到:

|
(16) |
右端项-R n通过方程(7)中单元积分和面积分得到。由于单元仅与周边单元有联系,左端项A=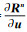
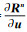
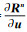
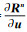

|
(17) |
采用块高斯赛德尔方法(BGS)方法对方程(17)进行求解:
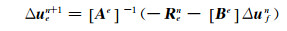
|
(18) |
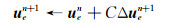
|
(19) |
其中,[ A e]表示单元e的对角块矩阵,[B e]表示非对角块矩阵,Δ u fn表示与单元e相邻的每个单元f在本时间步的Δ u 值。式(19)中,C∈[0, 1]为稳定因子,文中统一取0.5。
3 物面处理方法 3.1 弯曲物面构造方法与二维物面弯曲构造的方法相似[22],将三维物面边界的四边形单元从计算空间(x, y, z)转换到参考空间(ξ, η, ζ),在参考坐标平面构造曲面:
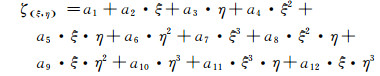
|
(20) |
系数根据点的坐标和加权法矢信息(式21)得到。
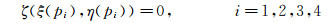
|
(21) |
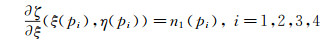
|
(22) |

|
(23) |
其中pi为计算空间四边形单元的顶点,n1(pi)、n2(pi)为顶点的加权偏导数项转换到参考平面后的数值。将参考空间构造得到的曲面映射到原(x, y, z)计算空间即得到重构的弯曲物面边界。区别于二维曲面重构后的连续和一阶导数连续的特性[18, 22],三维重构曲面仅有连续特性。具体曲面重构步骤如下:
1)在(x, y, z)计算空间根据加权方法得到四边形顶点的偏导数项Ni, i=1, 2, 3。
2)假设物面四边形的四个顶点处于同一平面,取其中三点pi(i=1, 2, 3)从计算空间(x, y, z)映射到(ξ, η, ζ)空间使满足式(21),可以得到两个坐标空间的映射矩阵T。根据映射矩阵T,将各顶点的法矢Ni转换到参考平面得到ni, i=1, 2, 3。根据ni计算得到n1(pj)和n2(pj):
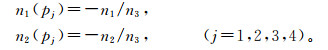
|
3)根据方程(21)~(23),求出系数a1~a12。
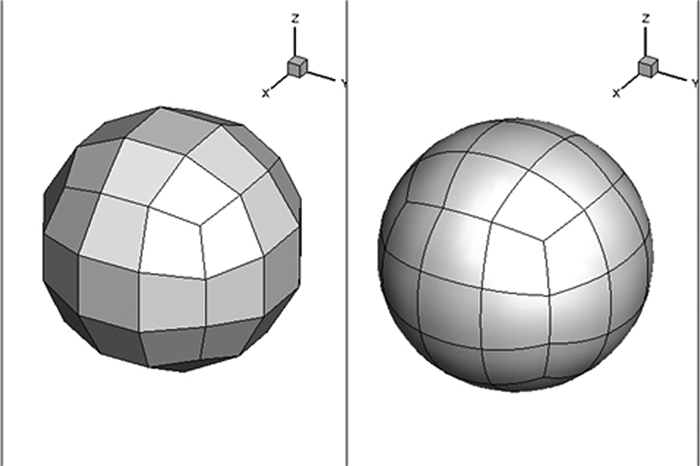
4)将(ξ, η, ζ)空间下的曲面信息映射到原(x, y, z)计算空间,得到高阶表述后的面单元(图 1)。
|
| 图 1 圆球的边界弯曲示意图 Fig. 1 Illustration of curved boundary representation method on a sphere |
实际计算中,为了尽可能满足步骤2中“四个顶点处于同一平面”的假设,在弯曲弧度较大的地方需要适当加密网格。
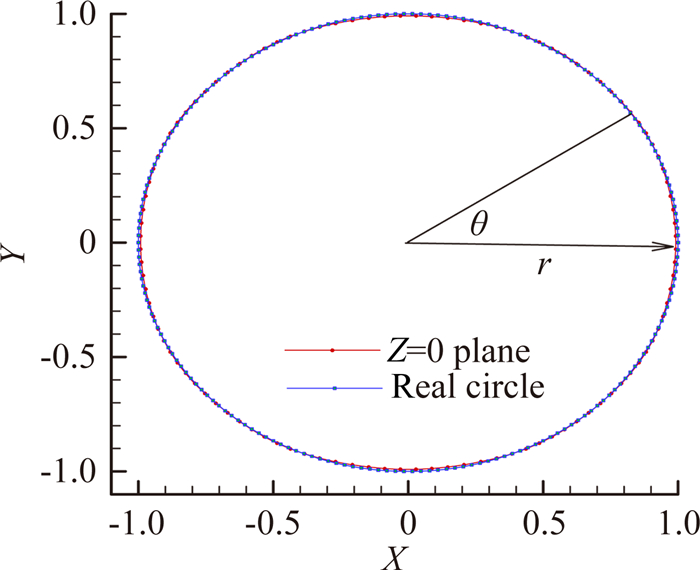
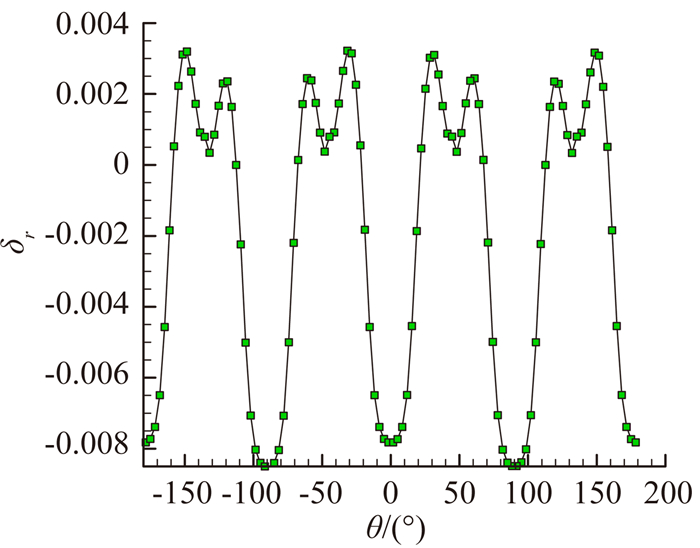
图 2给出了曲面构造后圆球Z=0截面与真实圆的误差,图 3给出了误差随角度的分布情况。该算例中Z=0截面的误差最大不足1%,实际计算中可以通过增加物面网格单元个数进一步减小曲面构造带来的误差。
|
| 图 2 曲面重构后Z=0截面的误差 Fig. 2 Illustration of the deviation on Z=0 plane |
|
| 图 3 曲面重构后Z=0截面的误差随角度的分布 Fig. 3 Illustration of the deviation according to the angle on Z=0 plane |
3.2 高阶单元映射
对于非物面单元,根据六面体单元的八个顶点进行线性映射:
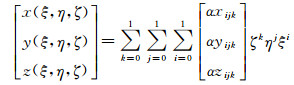
|
(24) |
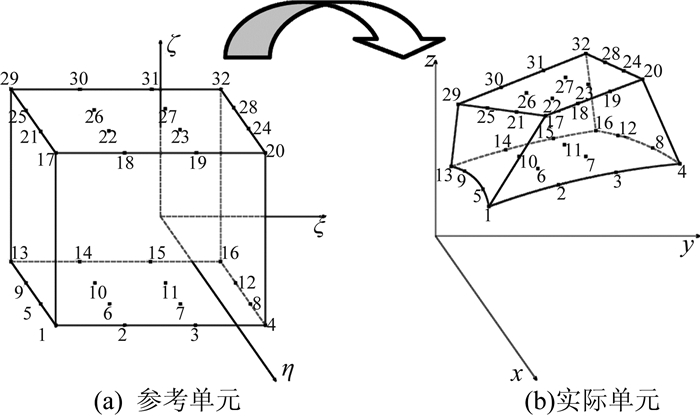
由于物面边界进行了弯曲重构,物面体网格单元采用32点进行高阶映射(图 4)。映射关系如下:
|
| 图 4 六面体单元映射点示意图 Fig. 4 Illustration of mapping points for 32-node hexahedral element |
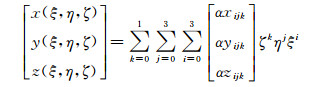
|
(25) |
根据已有坐标信息求出未知系数αxijk、αyijk和αzijk,即可得到单元映射雅克比矩阵及其他所需的映射关系。
4 数值结果与分析 4.1 三维含Bump管道内流采用该内流问题验证边界弯曲方法对间断有限元格式的精度影响。该算例计算区域的长度,宽度和高度分别为3、0.5、0.8。计算边界示意图见图 5,入口采用亚声速来流,马赫数M∞=0.5,出口为自由出流。两侧面和上表面为对称边界条件,下表面为滑移边界。下表面Bump的表达式为z=0.0625e-25x2, x∈(-1.5, 1.5)。由于该流动问题是求解欧拉方程,且几何和流动均光滑,所以理论上流场等熵,文中采用熵增作为衡量精度的标准。

|
| 图 5 含Bump管道内流边界示意图 Fig. 5 Illustration of boundary conditions for subsonic flow through a channel with a bump on the lower surface at M∞=0.5 |
熵增ε的定义如下:
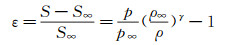
|
(26) |
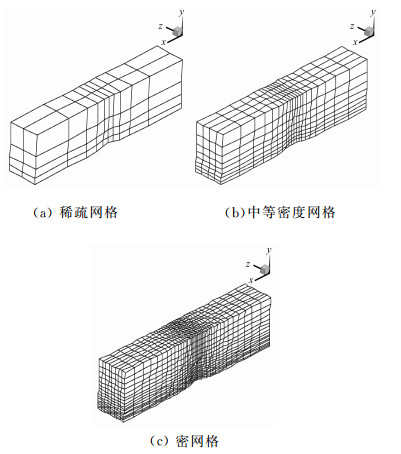
采用三套连续剖分加密的网格,网格点分布为11×5×3、21×9×5、41×17×9,单元数分别为80、640、5120,如图 6。
|
| 图 6 含Bump管道内流计算网格 Fig. 6 A sequence of three successively refined meshes used for computing subsonic flow through a channel with a bump |
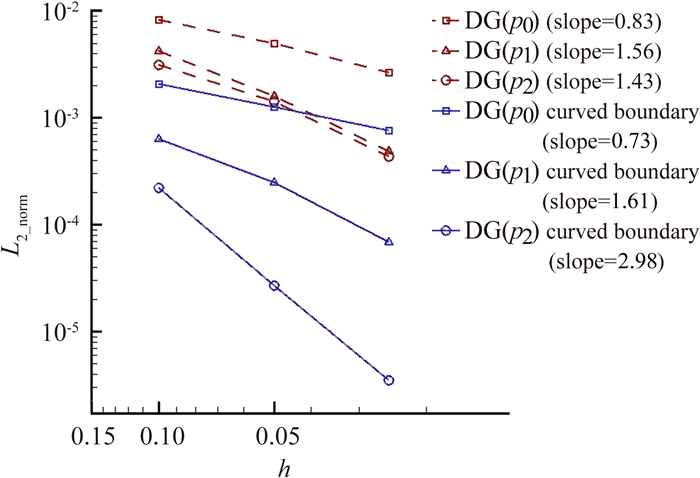
图 7为该算例的精度计算结果,横坐标表示网格的尺度。比较边界弯曲修正前后的精度曲线可知,当对弯曲几何的表述不足时,计算得到的熵增较大,且阶数较高时存在精度损失。边界弯曲修正方法提高了该算例的几何表述,从而空间离散达到了格式的设计精度。
|
| 图 7 三维含Bump管道内流精度测试收敛速率曲线 Fig. 7 Rates of convergence for subsonic flow through a channel with a bump |
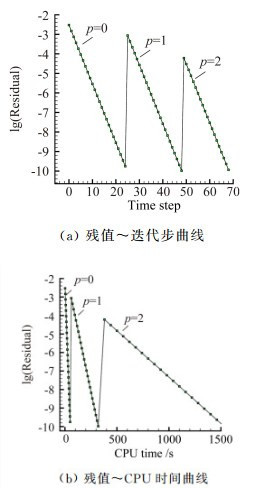
图 8为边界弯曲之后密网格上计算得到的三阶精度(p=2)的压力等值线图,可以看出,流场的等值线较光滑且对称性较好。图 9为边界弯曲后密网格上采用隐式计算方法(p=0~2)计算收敛所需的迭代步和计算时间,由于采用前一阶的计算结果作为下一阶数值计算的初值,计算时间和迭代步数大幅减少,密度残值收敛到-10量级仅需20个牛顿步。随着阶数的提高,自由度呈倍增加,计算所需的时间相应呈倍增加,在计算资源有限的情况下文中只计算到三阶精度(p=2)。

|
| 图 8 三维含Bump管道内流压力等值线图 Fig. 8 Pressure contours for subsonic flow through a channel with a bump |
|
| 图 9 三维含Bump管道内流密度残值收敛曲线 Fig. 9 Logarithmic density residual versus time step and CPU time for subsonic flow through a channel with a bump |
4.2 圆球黏性流动
选取低雷诺数圆球绕流算例验证边界弯曲方法在黏性流动中的适用性。自由来流条件为:马赫数 M∞=0.5,雷诺数Re∞=118。取半模进行数值计算,网格单元总数为9300,物面单元总数为192(图 10)。
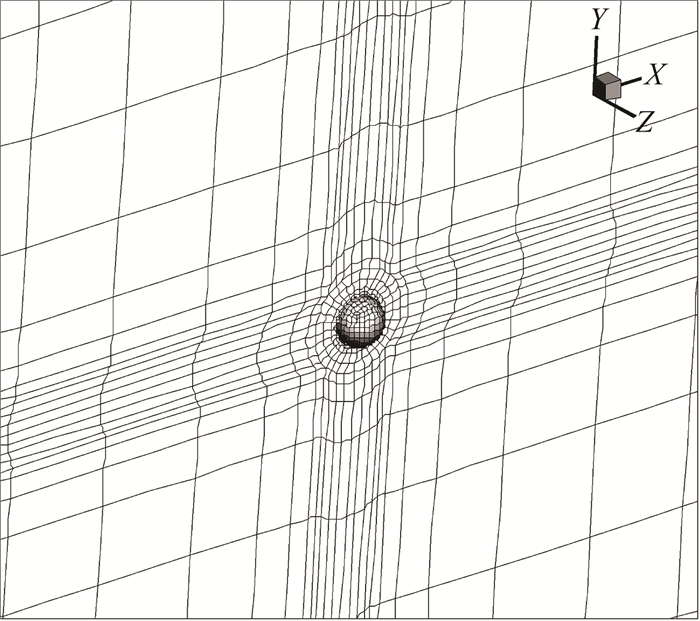
|
| 图 10 圆球黏性流动计算网格 Fig. 10 Mesh used for computing laminar flow past a sphere |
图 11为壁面弯曲前后三阶精度(p=2)下计算得到的球表面及Z=0对称面的压力等值线图。可以看出,准确的壁面表述对DG方法较为重要,壁面弯曲后计算得到的等值线较为光滑和对称。图 12为计算得到的Z=0对称面的压力系数曲线,经过壁面弯曲修正后得到的压力系数曲线较为光滑连续。

|
| 图 11 圆球黏性流动压力等值线 Fig. 11 Computed pressure contours in the flow field |
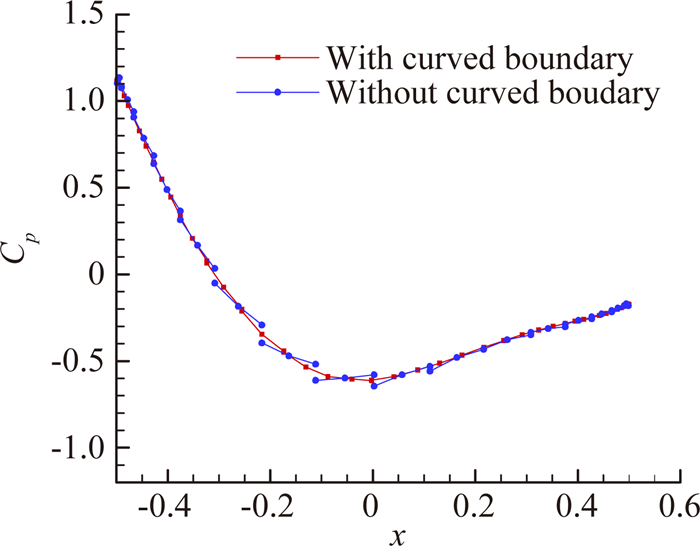
|
| 图 12 圆球黏性流动Z=0截面计算压力系数曲线比较 Fig. 12 Comparison of computed pressure coefficient on Z=0 plane |
图 13为壁面弯曲前后三阶精度(p=2)的密度残值下降曲线。可以看出,物面弯曲对隐式方法的收敛效率同样有较大影响。

|
| 图 13 三维圆球黏性流动密度残值收敛曲线 Fig. 13 Logarithmic density residual versus time step for flow past a sphere |
4.3 旋转流线体绕流
选取High-order CFD Workshop[25]的三维旋转流线体层流算例验证文中的边界弯曲方法对于较复杂曲面的适用性。计算自由来流条件为:马赫数M∞=0.5,雷诺数Re∞=5000,迎角α=1°。计算网格单元总数为18294,物面单元总数为582(图 14),在物面前缘和后缘进行网格局部加密。图 15和图 16分别给出了三阶精度(p=2)的计算等密度线图和等马赫线图,即使物面网格相对稀疏,采用边界弯曲方法后得到的结果依然较为光滑。图 17为本算例的密度残值收敛曲线,由于采用了高效的隐式计算方法,残值在30个牛顿步内均收敛到-6量级以下。

|
| 图 14 旋转流线体黏性流动计算网格 Fig. 14 Mesh used for computing laminar flow past a streamlined body |
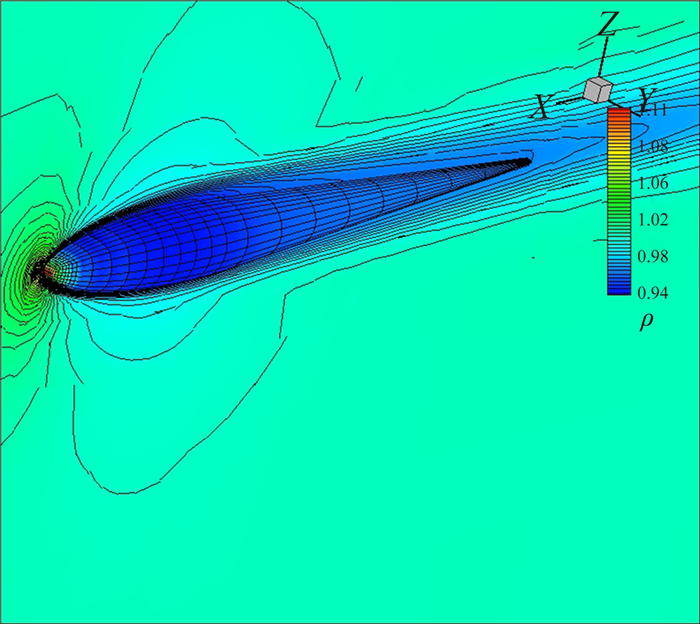
|
| 图 15 旋转流线体黏性流动密度等值线图 Fig. 15 Density contours for laminar flow past a streamlined body |
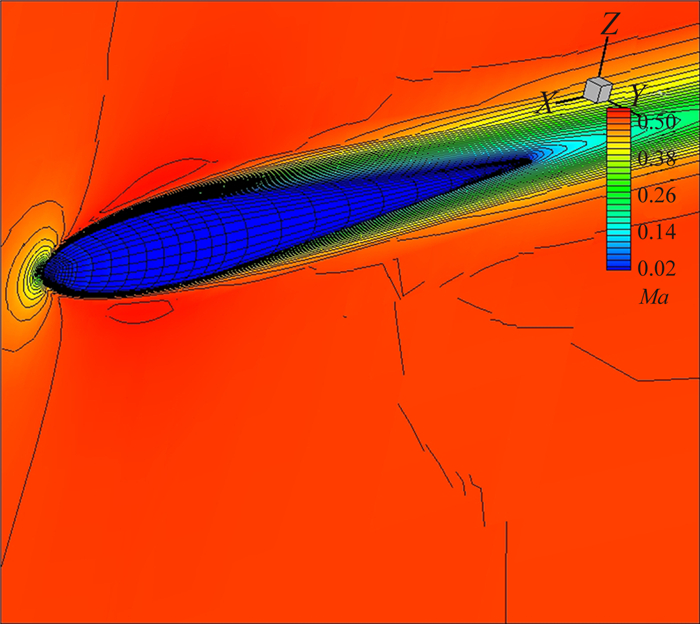
|
| 图 16 旋转流线体黏性流动马赫数等值线图 Fig. 16 Mach number contours for laminar flow past a streamlined body |

|
| 图 17 三维旋转流线体黏性流动密度残值收敛曲线 Fig. 17 Logarithmic density residual versus time step for laminar flow past astreamlined body |
5 结论
本文将间断有限元方法拓展到三维可压缩气动方程组的求解中。与以往一些数值方法的区别在于:在三维情况下对边界四边形网格单元进行了弯曲重构,更准确地表述了物面特征,从而使得DG方法在相对稀疏的网格上就能得到高精度的数值解。同时采用了鲁棒可靠的隐式方法,缩短了计算时间,提高了计算效率。对Euler方程和Navier-Stokes方程数值求解的结果表明,文中的壁面弯曲方法能较好地应用于间断有限元方法且有很好的鲁棒性。后续将设计高效的并行算法进一步提高计算效率,同时考虑加入湍流模型研究更复杂的流动问题。
| [1] | Wang Z J. High-order methods for the Euler and Navier-Stokes equations on unstructured grids[J]. Progress in Aerospace Sciences, 2007, 43(1):1–41. |
| [2] | Cockburn B, Shu C W. The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems[J]. Journal of Computational Physics, 1998, 141(2):199–224. DOI:10.1006/jcph.1998.5892 |
| [3] | Cockburn B, Shu C W. The local discontinuous Galerkin method for time-dependent convection-diffusion systems[J]. SIAM Journal on Numerical Analysis, 1998, 35(6):2440–2463. DOI:10.1137/S0036142997316712 |
| [4] | Cockburn B, Shu C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J]. Journal of scientific computing, 2001, 16(3):173–261. DOI:10.1023/A:1012873910884 |
| [5] | Cockburn B, Li F, Shu C W. Locally divergence-free discontinuous Galerkin methods for the Maxwell equations[J]. Journal of Computational Physics, 2004, 194(2):588–610. DOI:10.1016/j.jcp.2003.09.007 |
| [6] | Bassi F, Rebay S. High-order accurate discontinuous discontinuous finite element solution of the 2D Euler equations[J]. Journal of Computational Physics, 1997, 138(2):251–285. DOI:10.1006/jcph.1997.5454 |
| [7] | Bassi F, Rebay S. A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 1997, 131(2):267–279. DOI:10.1006/jcph.1996.5572 |
| [8] | Bassi F, Crivellini A, Rebay S, et al. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ω turbulence model equations[J]. Computers & Fluids, 2005, 34(2):507–540. |
| [9] | Lyu Hongqiang, Sun qiang, Qin Wanglong. 3D numerical solution of aero-noise with high-order discontinuous Galerkin method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 30(3):227–231. |
| [10] | Xia Y, Luo H, Nourgaliev R. An implicit Hermite WENO reconstruction-based discontinuous Galerkin method on tetrahedral grids[J]. Computers & Fluids, 2014, 96:406–421. |
| [11] | Luo H, Xia Y, Li S, et al. A Hermite WENO reconstruction-based discontinuous Galerkin method for the Euler equations on tetrahedral grids[J]. Journal of Computational Physics, 2012, 231(16):5489–5503. DOI:10.1016/j.jcp.2012.05.011 |
| [12] | Luo H, Luo Luqing, Nourgaliev R, et al. A reconstructed discontinuous Galerkin method for the compressible Navier-Stokes equations on arbitrary grids[J]. Journal of Computational Physics, 2010, 229(2):6961–6978. |
| [13] | Zhu J, Qiu J. WENO Schemes and their application as limiters for RKDG methods based on trigonometric approximation spaces[J]. Journal of Scientific Computing, 2012:1–39. |
| [14] |
Zhang Laiping, Li Ming, Liu Wei, et al. Recent development of high order DG/FV hybrid methods[J].
Acta Aerodynamica Sinica, 2014, 32(6):717–726.
(in Chinese) 张来平, 李明, 刘伟, 等. 基于非结构/混合网格的高阶精度DG/FV混合方法研究进展[J]. 空气动力学学报, 2014, 32(6) : 717–726. |
| [15] | Li S. A parallel discontinuous Galerkin method with physical orthogonal basis on curved elements[J]. Procedia Engineering, 2013, 61:144–151. DOI:10.1016/j.proeng.2013.07.107 |
| [16] | Wang L, Anderson W K, Erwin J T, et al. Solutions of high-order methods for three-dimensional compressible viscous flows[C]//42nd AIAA Fluid Dynamics Conference and Exhibit. New Orleans, 2012. |
| [17] | Hartmann R, Held J, Leicht T, et al. Discontinuous Galerkin methods for computational aerodynamics-3D adaptive flow simulation with the DLR PADGE code[J]. Aerospace Science and Technology, 2010, 14(7):512–519. DOI:10.1016/j.ast.2010.04.002 |
| [18] | Landmann B, Kessler M, Wagner S, et al. A parallel, high-order discontinuous Galerkin codes for laminar and turbulent flows[J]. Computers & Fluids, 2008, 37(2):427–438. |
| [19] | Lübon C, Keßler M, Wagner S. A parallel CFD solver using the discontinuous Galerkin approach[M]//High Performance Computing in Science and Engineering, Garching/Munich 2007. Springer Berlin Heidelberg, 2009:291-302. |
| [20] |
Yu Jian, Yan Chao. Discontinuous Galerkin method based on artificial viscosity[J].
Acta Aerodynamica Sinica, 2013, 31(3):371–375.
(in Chinese) 于剑, 阎超. 基于人工粘性的间断Galerkin有限元方法[J]. 空气动力学学报, 2013, 31(3) : 371–375. |
| [21] |
Xia Yidong, Wu Yizhao, Lyu Hongqiang, et al. Parallel computation of a high-order discontinuous Galerkin method on unstructured grids[J].
Acta Aerodynamica Sinica, 2011, 29(5):537–541.
(in Chinese) 夏轶栋, 伍贻兆, 吕宏强, 等. 高阶间断有限元法的并行计算研究[J]. 空气动力学学报, 2011, 29(5) : 537–541. |
| [22] |
Qin Wanglong, Lyu Hongqiang, Wu Yizhao. High-order discontinuous Galerkin solution of N-S equations on hybrid mesh[J].
Chinese Journal of Theoretical and Applied Mechani, 2013, 45(6):987–991.
(in Chinese) 秦望龙, 吕宏强, 伍贻兆. 基于混合网格的高阶间断有限元黏流数值解法[J]. 力学学报, 2013, 45(6) : 987–991. |
| [23] |
Qin Wanglong, Lyu Hongqiang, Wu Yizhao. Discontinuous Galerkin solution of RANS equations on curved mesh[J].
Acta Aerodynamica Sinica, 2014, 32(5):581–586.
(in Chinese) 秦望龙, 吕宏强, 伍贻兆. 弯曲网格上的间断有限元湍流数值解法研究[J]. 空气动力学学报, 2014, 32(5) : 581–586. |
| [24] | Toro E F, Spruce M, SpearesW. Restoration of the contact surface in the HLL-Riemann solver[J]. Shock Waves, 1994, 4(2):25–34. |
| [25] | High-order CFD Workshop. Problem C2.3. Analytical 3D Body of Revolution[OL/EB]. http://www.as.dlr.de/hiocfd/case_c2.3.html |



