动导数是飞行器气动力系数和气动力矩系数对飞行器无因次旋转角速度或姿态角变化率的导数,是飞行器研制控制系统设计和动态品质分析不可缺少的原始气动参数[1],它是关系到飞行器的飞行品质、自动驾驶控制系统控制律设计以及安全飞行的一个重要方面。长期以来,国内外空气动力研究机构一直致力于飞行器的动导数风洞试验技术研究和数值模拟分析工作,并为各类航空航天飞行器的研制提供了大量的基础试验数据[2-14]。同高性能计算机数值模拟手段相比,风洞试验仍然具有直观、可靠的优点,在将来的很长一段时间内将难以替代。但是到目前为止,大量的资料显示[15-18],动导数风洞试验相似准则的模拟、试验系统的设计以及数据误差的分析与控制等方面还存在较多的困难,动导数试验系统的精准度难以保证。
近年来,大型运输机、先进战斗机、推进与机体一体化布局等现代高性能飞行器的研制,为国内空气动力研究机构风洞地面模拟试验能力提出了更高的要求。就飞行器动态气动特性风洞模拟而言,同1m量级风洞动导数试验技术相比,2m量级风洞进行动导数试验具有模型尺度大、试验Re数高、外形模拟更加准确(由于振动空间给模型带来的局部修形少)、能够更真实地模拟飞行减缩频率(减缩频率是动导数试验研究非常关键的参数,达到与飞行条件一致最为理想,尺度为2.4m的风洞试验模型减缩频率可比相同外型在1.2m风洞进行动导数试验时提高50%左右)以及支撑系统干扰较小等优点,因此获取的动导数数据也会更加可靠。但是,在2m量级高速风洞开展动导数试验研究也将面临更大的困难,主要体现在模型尺度大,为满足质量控制的要求,其强度和刚度不易保证;其二,大尺度模型的稳态载荷或者感受到的高速风洞冲击载荷相对较大,导致试验装置的传动机构设计以及α、β耦合双转轴支撑结构设计非常困难;其三,大载荷驱动与控制系统的设计将会面临测试天平的较强电磁干扰,这会直接影响试验系统的精准度水平的提高。为此,为满足现代先进飞行器的动稳定性研究要求,提高在2m量级高速风洞开展动导数试验的能力,中国空气动力研究与发展中心高速所在2.4m跨声速风洞(FL-26)和2米超声速风洞(FL-28)开展了专项动导数试验技术研究工作。
1 试验原理及试验系统设计 1.1 试验原理2m量级高速风洞动导数试验,基于试验系统的安全考虑,一般建议选择强迫振动试验方法进行。强迫振动法是使用激振器强迫模型在某一自由度下作固定频率和固定振幅的简谐振动(偏转或平移)运动。根据达朗贝尔原理,在任一瞬间,作用在整个弹性系统上的各种力矩,即机械阻尼力矩、弹性恢复力矩、气动静力矩、气动阻尼力矩、惯性力矩和外加的强迫力矩等应保持平衡。按照此原理求解振动方程,即可获得所需要的动导数数据(参见后文数据处理公式)。强迫振动法可以测量各类动导数,而且能测量负阻尼导数,并能较方便地调整振动频率和振幅,此外,该方法既可采集一定时间的数据平均,又可利用相关滤波原理,有效地抑制风洞气流噪声的影响,确保获得的动导数试验数据具备较高的精准度。本文基于此试验原理,开展了相关的研究工作。
1.2 试验系统设计高速风洞动导数试验系统主要包括试验模型系统、模型支撑系统、作动机构系统、驱动与控制系统、测试天平系统、高速动态数据采集与处理系统等部分组成。图 1给出了2m量级高速风洞的动导数试验系统构成框图,从模型风洞支撑方案来看,可实现基本纵横向的状态试验;试验装置按照模型振动方向分为滚转、俯仰和偏航三套;试验系统的测控部分主要包括试验数据的高速动态采集系统、电机驱动与控制系统以及数据的处理与分析系统;另外,为保证试验系统的可靠性,还研制了专用的地面静态校准装置和用于考核验证的动态标准模型。从整个系统的设计来看,具有环节多、测控设备多、机械传动结构复杂等特点,所以在试验中数据的精准度及系统的可靠性等极不容易控制。系统研制完成后可实现模型俯仰、偏航以及滚转三个方向的直接阻尼导数、交叉阻尼导数以及交叉耦合阻尼导数的测量,直接阻尼导数重复性精度优于15%。
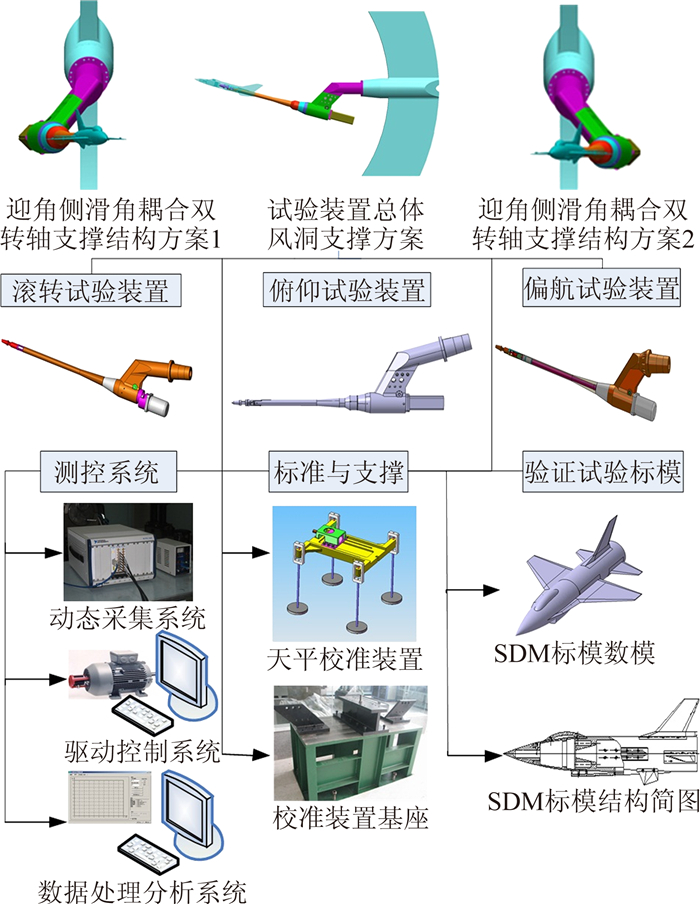
|
| 图 1 2m量级高速风洞动导数试验系统构成框图 Fig. 1 Block diagram of dynamic derivative test system in 2 meter scale high speed wind tunnels |
2 关键技术及解决措施 2.1 试验模型研制
同常规风洞测力试验模型相比,为了避免振动过程中模型惯性载荷的影响,在模型设计的过程中要求尽可能使其质心位置调整至机构的振动中心。并且,为了进一步提高支撑系统的固有频率,降低系统振动过程中的共振风险,控制模型的重量是动导数试验中尤其重要。目前,常用的动导数模型制造材料有两种,其一是航空铝材,其二是复合材料。这两种材料共同的特点是比重小,强度高,而且制造成本相对较低,是比较理想的模型制造材料。
对于2m量级风洞的动导数模型而言,翼展尺度约为1m,既要控制模型重量,还要保证强度和刚度,在设计过程中必须要注重细节,并且借助有限元分析等手段进行辅助设计。图 2给出了设计完成的SDM结构简图,模型总长约为933mm,展长约为604mm。本套模型采用航空铝材制作,实物模型的重量小于10kg,但这也基本是2m量级风洞动导数试验模型质量的最大值。对于展长更大的模型而言,航空铝材也难以满足质量控制要求,从而不得不选用质量更轻的复合材料进行制作,并在模型的尺寸控制及外形模拟等方面需要进行严格控制,以满足相似性的设计要求。
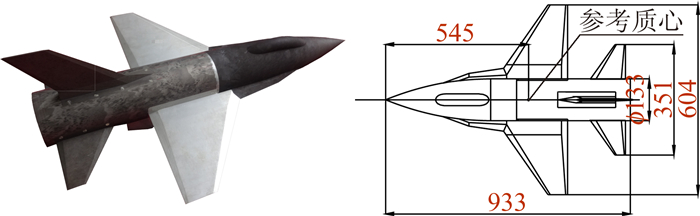
|
| 图 2 动导数试验SDM模型 Fig. 2 SDM model for dynamic derivative test |
2.2 试验支撑装置及传动机构设计
图 3给出了2m量级风洞俯仰/偏航动导数试验装置和滚转动导数试验装置结构简图。为了满足迎角、侧滑角连续变化的需要,在支撑装置的设计中采用了双转轴的设计思路,即通过前轴、后轴0°~360°的连续组合变化实现不同模型姿态角的试验测量。同常规风洞双转轴设计不同,本套双转轴装置还要兼顾作动机构中部传动杆的低阻尼、无间隙转动(间隙尽可能小),这极大地增加了机构定位、锁紧、安装拆卸的难度。作为支撑装置的另外一部分,尾支杆的设计同样存在较大的困难,主要体现在其是模型载荷的主要承载单元,但为了不对模型尾部支撑造成过大的外形破坏,支杆的直径还要尽可能的小,并且支杆内部还要布置传动杆、连接测力天平和布置天平的测量线等。尾支杆的强度和刚度是决定支撑系统安全以及提高系统固有频率的重要因素。
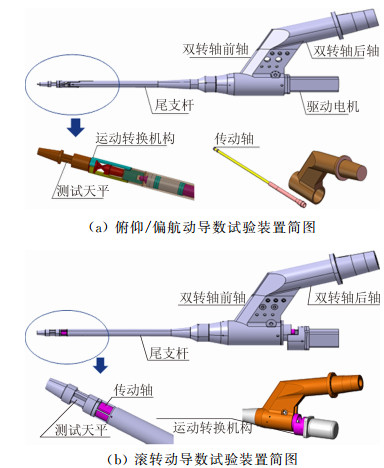
|
| 图 3 动导数试验装置简图 Fig. 3 Test devices of dynamic derivative test |
在试验装置的传动结构设计中,运动转换机构的传动杆、偏心球头等是关键部件。设计的难点在于需要解决大载荷条件下传动部件的可靠性问题,以及传动过程中间隙控制对试验系统结果的精准度的影响。为了验证设计结构,优化设计方案,本文采用有限元分析软件对试验装置开展了结构静力学和动力学特性分析。图 4给出了试验装置静力学分析的网格模型示意图,重点展示了偏心球头和传动连接件的网格模型。利用ABAQUS软件对整个支撑装置装配模型进行静力分析,获得了天平、传动球头以及传动轴连接部分的应力分析结果。分析认为在传动偏心球头的地方,在工作状态下,此处应力区域处于脉动应力状态,所以容易产生疲劳破坏。为避免疲劳破坏对装置运行产生影响,设计中通过增加接触面积有效提高了接触区域的接触强度。
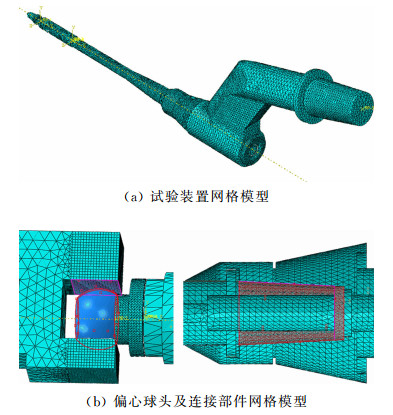
|
| 图 4 试验装置静力学分析网格模型 Fig. 4 Statics analysis grid model of the test devices |
在试验装置静力学特性分析完成后,为了确定在静态载荷和动态载荷作用下的模型支撑装置的机构动力学特性,本文应用MSC.ADAMS/VIEW软件进行了分析。这里以一组静态载荷为例,给出分析的过程。假定模型支撑装置承受的静态载荷为:法向力12000N,轴向力1000N和俯仰力矩600N·m,作用点位于天平力矩元件中心位置。在此载荷作用下,选择不同的偏心头位置摩擦系数以及电机不同驱动频率,计算偏心头处的摩擦力和力矩、电机驱动力矩以及力矩平衡杆振动角位移等。设置偏心球头与位移元件间接触的静摩擦系数为0.15,动摩擦系数为0.1,电机驱动传动轴旋转频率为4Hz,运用ADAMS/SOLVER进行机构运动学仿真计算。
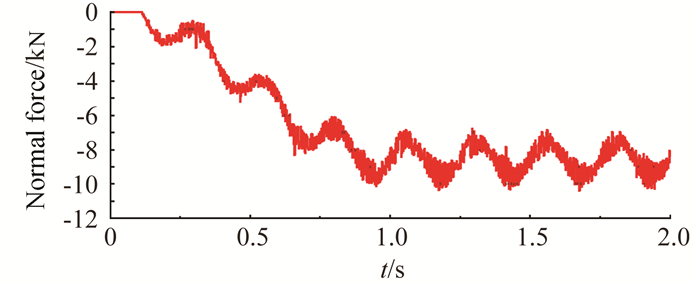
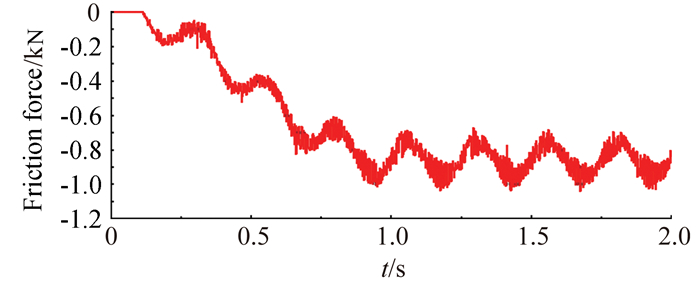
图 5、图 6显示了偏心球头与位移元件间接触法向力和摩擦力随时间变化曲线。可见,接触法向力产生源有两个:一是外载荷作用,二是偏心运动。第1s时外载荷达到最大值,此时外载荷引起的接触法向力达到最大。1s以后主要是偏心运动的作用,引起接触法向力类正弦变化,平均值约8700N,幅值约1780N,频率4Hz。接触摩擦力由接触法向力产生,也呈类正弦变化,平均值约870N,幅值约180N。
|
| 图 5 接触法向力随时间变化曲线 Fig. 5 Contact normal force curves along time |
|
| 图 6 接触摩擦力随时间变化曲线 Fig. 6 Friction force curves along time |
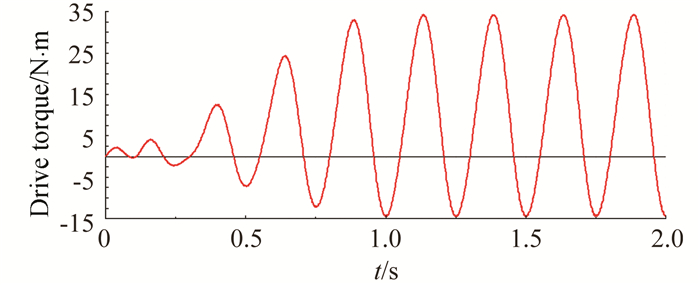
图 7给出了电机驱动传动轴的力矩随时间变化曲线,可知,电机驱动传动轴力矩变化范围为-15N·m~34N·m,与传动轴承受接触力扭矩大小基本相同,也表明电机驱动力矩满足要求。
|
| 图 7 电机驱动力矩随时间变化曲线 Fig. 7 Motor drive torque curves along time |
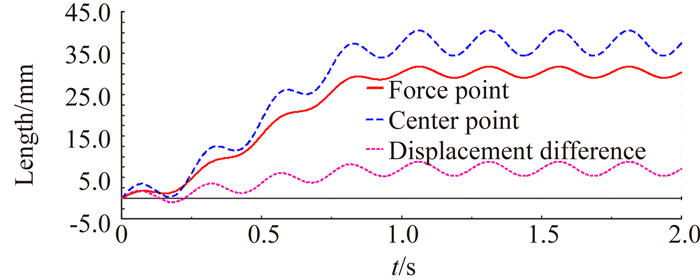
力矩元件的端面中心点以及外载荷作用点的垂直位移随时间变化曲线如图 8所示,其中两点间距为129mm。图 8同时给出了两点垂直位移之差随时间变化曲线,1s时刻后呈类正弦变化规律,振幅约1.73mm,频率为4Hz。将振幅除以两点间距,即得到位移元件振动角度幅值为:
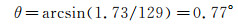
|
(1) |
|
| 图 8 振动位移随时间变化曲线 Fig. 8 Vibration displacement curves along time |
采用静力学和动力学特性分析手段可以获得已知载荷作用下的试验装置工作性能,这也为装置使用的边界载荷的确定提供了一个有效的手段,在优化设计装置的同时,进一步降低了试验装置在风洞试验过程中的运行风险。
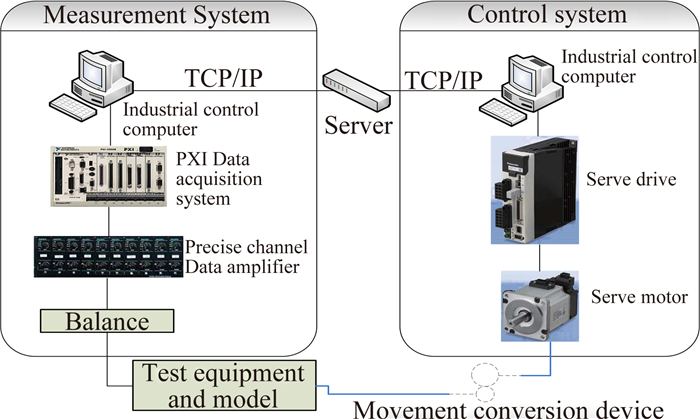
2.3 测量与驱动控制系统设计图 9给出本项动导数试验系统的控制与测量系统构成框图。对于系统的测量设备,经过调研,采用了PXI总线系统,相对VXI总线系统,该系统具有系统带宽高、结构尺寸紧凑的特点。在控制系统设计中,重点在于驱动电机的研制。2m量级风洞动导数试验载荷较大,常用的步进电机驱动力矩无法满足试验要求,且步进电机在特定运行条件下,转速不平稳,造成力矩信号的信噪比降低,并且步进电机不允许过载,否则会造成失步。相对而言,伺服电机转速平稳,驱动力矩大,允许瞬时过载,有利于提高信噪比,而伺服电机干扰问题可以采用信号线隔离、屏蔽和数据滤波技术加以解决。因此,2m量级风洞动导数试验装置拟采用伺服电机的驱动方式,并采用变频电源技术实现振动频率要求。
|
| 图 9 测控系统联调框图 Fig. 9 Measurement and control system interacted diagram |
2.4 数据处理系统设计
此处以单自由度俯仰振动为例,给出数据处理系统设计的基本原理。模型作单自由度俯仰振动运动时,其振动运动微分方程式为:
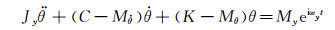
|
(2) |
式中:
Jy——模型绕y轴的转动惯量;
θ——振动角位移;
C——振动系统的机械阻尼力矩导数;
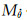
Mθ——气动俯仰恢复力矩导数;
My——绕y轴力矩;
ωy——模型绕y轴转动角速度;
K——弹性铰链提供的恢复力矩系数。
该方程是一个常系数、线性、二阶非齐次微分方程。方程的解由两部分组成,一部分是方程所对应的齐次形式的通解,另一部分是非齐次方程的特解。齐次方程的通解随时间很快就衰减掉了,因此关心的是其特解,即:
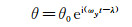
|
(3) |
由此可见:
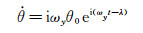
|
(4) |
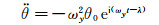
|
(5) |
代入方程(2)得:
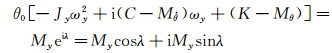
|
(6) |
由上式两端的虚部相等,可得模型的气动俯仰阻尼力矩导数为:
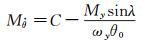
|
(7) |
同理,由式(6)两端的实部相等,可得模型的气动俯仰恢复力矩导数为:
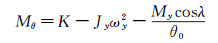
|
(8) |
无因次化动导数:
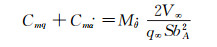
|
(9) |
为了考核试验系统的可靠性和获取试验结果的精准度水平,本文选择了具有代表性的SDM标模(Standard Dynamic Model,北大西洋公约组织统一使用的动态试验标模)和某大型飞机模型进行了试验研究。两期试验均获得了较好的试验结果,表明试验系统研制获得了成功。
3.1 试验系统SDM标模验证风洞试验研究系统验证性试验主要在气动中心高速所FL-26跨声速风洞(试验段截面尺寸2.4m×2.4m)和FL-28超声速风洞(试验段截面尺寸2m×2m)中完成。模型均选择高强度轻质材料(航空铝材或复合材料)制作,总重量控制在10kg以内。验证试验的主要内容包括试验系统结果的精度、准度、系统的可靠性以及设计技术指标的实现情况等。
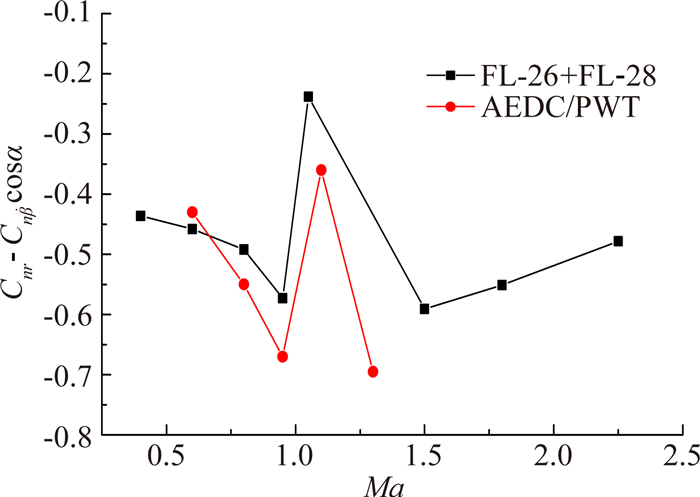
图 10给出了SDM标模在FL-26风洞和FL-28风洞的试验照片,图 11、图 12分别给出了0°迎角时,模型俯仰/偏航动导数随Ma数变化的试验结果曲线。从图 11和图 12来看,模型俯仰和偏航阻尼导数在跨声速附近出现较大的波动,且阻尼最大值出现在该区域;随Ma数进一步增加,在超声速区模型阻尼逐渐降低,但是曲线变化趋势较为平缓,这种规律与常规飞行器静导数的变化规律一致。另外,还可以看出,试验结果同国外风洞(AEDC/PWT)资料值相比,一致性较好,表明了试验系统结果的准确性。

|
| 图 10 SDM标模风洞动导数试验照片 Fig. 10 photo of the sdm model taken in the dynamic derivative test in fl-28 wind tunnel |
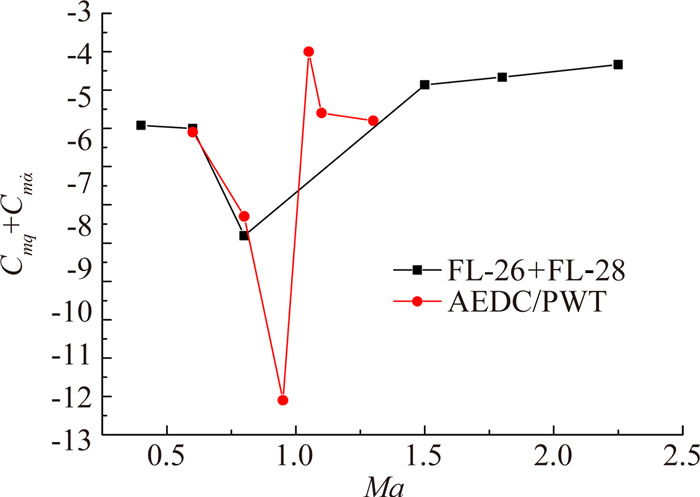
|
| 图 11 SDM标模俯仰动导数随Ma数变化曲线(α=0°) Fig. 11 Pitch dynamic derivative test results of the SDM model curves along Ma number(α=0°) |
|
| 图 12 SDM标模俯仰动导数随Ma数变化曲线α=0° Fig. 12 Yaw dynamic derivative test results of the SDM model curves along Ma number(α=0°) |
图 13给出了本套试验系统Ma=0.6时SDM标模滚转动导数随迎角的变化曲线,并同时给出了国外风洞的试验结果。可见,随迎角变化,试验结果与国外资料值的变化规律一致,且量值相当,验证了试验滚转动导数试验装置的可靠性。

|
| 图 13 SDM标模滚转动导数随迎角曲线(Ma=0.6) Fig. 13 Roll dynamic derivative test results of the SDM model curves along angel(Ma=0.6) |
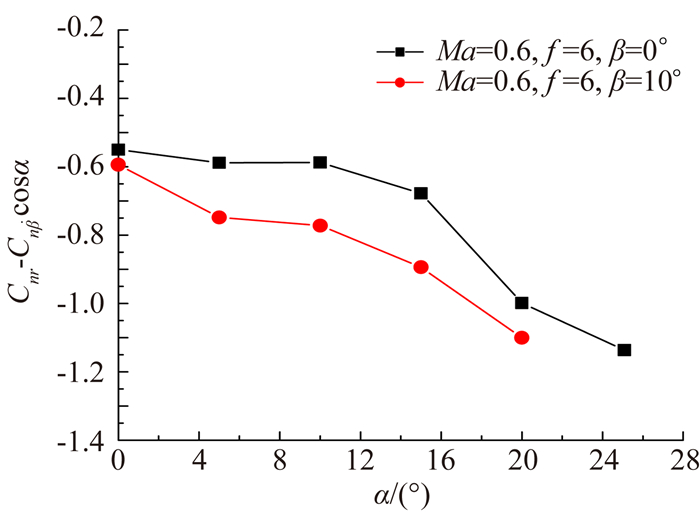
为了验证试验系统的迎角和侧滑角耦合的试验能力,本文利用SDM标模进行了相关研究。图 14给出了迎角α=0°~26°,侧滑角β=0°和β=10°条件下的SDM标模动导数试验结果曲线,由此图可见,在0°迎角时,侧滑角的改变对偏航动导数影响不大,但随迎角的增加,改变侧滑角会导致模型的阻尼增加,这与飞机模型横向阻尼面积的改变相关,总体来看,试验数据的规律合理,达到了预期的设计技术指标要求。
|
| 图 14 SDM标模偏航动导数随迎角曲线(β=0°,10°) Fig. 14 Yaw dynamic derivative test results of the SDM model curves along angel(β=0°, 10°) |
为了进一步验证试验系统的精度水平,本文在不同模型拆装条件下完成了SDM标模重复性试验。表 1给出了迎角α=0°、Ma=0.6时7次重复性试验结果,可见,测试值相对于均值的偏差均小于10%,对于高速动导数试验系统而言,可认为精度已达到较好水平。
| 测值 | -0.258 | -0.26 | -0.25 | -0.243 | -0.287 | -0.285 | -0.26 |
| 误差 | 3% | 2% | 5% | 8% | 9% | 8% | -2% |
3.2 某大展弦比飞机模型动稳定性风洞试验研究
试验系统研制完成以后,首次在FL-26风洞进行了某飞机模型的动稳定性试验研究。同SDM标模相比,该飞机模型展弦比更大,物面绕流特征更加复杂,进一步增加了动导数测试结果的精度和准度。图 15对比给出了常规测力与俯仰动导数的测试结果曲线,可见,失速迎角附近,升力系数非线性变化明显,此时获得的动导数结果也呈现较大的波动变化,甚至出现动不稳定的结果。为了验证在复杂流动条件下,动导数测试系统工作的稳定性,本文进行了Ma=0.74和Ma=0.79的试验研究。从图 15可见,试验的两个Ma数再现了同一动态气动特性变化规律,并且同常规静态测力反映的流动现象一致,充分说明测试结果可靠,至于反映出的动不稳定现象,还需要做进一步的研究。

|
| 图 15 某飞机模型俯仰动导数与升力系数随迎角变化曲线 Fig. 15 Pitch dynamic derivative and lift coefficient results of the transport model curves along angel |
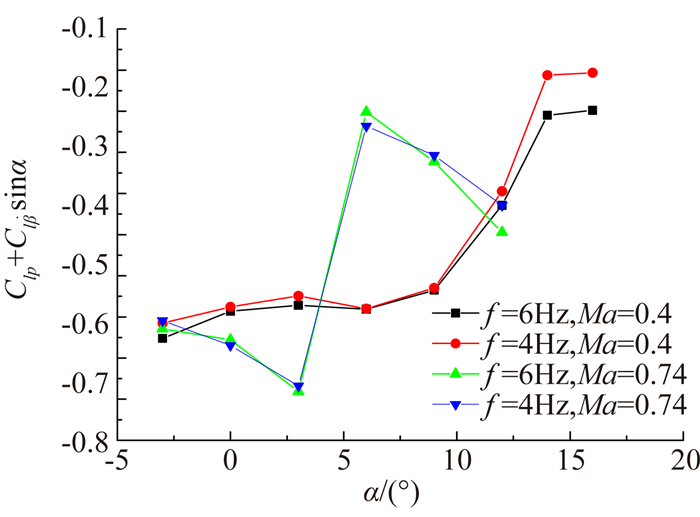
针对飞机模型非定常流动比较明显的实际情况,本文还研究了试验频率改变对测试结果的影响,试验Ma=0.4和Ma=0.74。图 16给出了滚转动导数的试验研究结果,可见,试验频率的改变对测试结果的影响较小,而且在Ma=0.74,容易出现失速绕流的情况下,试验系统仍然获得了规律一致的结果。
|
| 图 16 某飞机模型滚转动导数随迎角变化曲线 Fig. 16 Roll dynamic derivative test results of the transport model curves along angel |
4 结论
本文成功建立了2m量级大尺度风洞强迫振动动导数试验试验技术,通过SDM标模和某飞机模型的考核验证试验,有如下的结论:
1) 采用比重小、强度高的航空铝材和复合材料可有效控制2m量级风洞大尺度动导数模型的质量,而且模型的强度和刚度满足高速风洞试验要求;
2) 通过静力学和动力学以及运动学仿真等技术手段进一步优化了试验支撑系统、作动机构的设计,并确定了风洞调试试验系统可以承载的边界载荷,极大地降低了高速风洞试验的风险;
3) 测量与控制以及数据处理系统的合理设计保证了系统运行的可靠性,提高了试验结果的精准度水平。
4) SDM标模的验证表明,试验结果与资料值一致性较好,且测试值相对于均值的偏差均小于10%;某飞机模型的验证性试验也表明了在大载荷、复杂流动条件下系统工作的稳定性和可靠性。
| [1] |
Wang Faxiang.
High speed wind tunnel test[M]. Beijing: National Defence Industry Press, 2001 : 344 -362.
(in Chinese) 王发祥. 高速风洞试验[M]. 北京: 国防工业出版社, 2001 : 344 -362. |
| [2] | Hanff E S. Direct forced-oscillation techniques for the determination of stability derivatives in wind tunnel[R]. AGARD LS-114, Paper 4, 1981. |
| [3] | Cyram B. Sting interference effects on the static, dynamic, and base pressure measurements of the standard dynamic model aircraft at Mach numbers 0.3 through 1.3[R]. AEDCTR-81-3, 1981. |
| [4] | Coulter S M, Marquart E J. Cross and cross-coupling derivative measurements on the standard dynamic at AEDC. AIAA-82-0596[R]. Reston:AIAA, 1982. |
| [5] |
Zhao Zhongliang, Ren Bin. High angle of attack dynamic derivative experiment technique in 1.2m wind tunnel[J].
Experiments and Measurements in Fluid Mechanics, 1998, 12(1).
(in Chinese) 赵忠良, 任斌. 1.2m风洞大攻角动导数试验技术[J]. 流体力学实验与测量, 1998, 12(1). |
| [6] |
Zhao Zhongliang, Ren Bin, Huang Xuhui, et al. Investigation on model dynamic stability derivatives test techniques in trans-supers-hypersonic wind tunnels[J].
Acta Aeronautica et Astronautica Sinica, 2000, 21(1):52–54.
(in Chinese) 赵忠良, 任斌, 黄叙辉, 等. 跨超、高超声速风洞模型动导数试验技术研究[J]. 航空学报, 2000, 21(1) : 52–54. |
| [7] | Makoto Ueno, Hitoshi Miwa. New dynamic stability equipment for transonic wind tunnel testing at NAL. AIAA 2001-0406[R]. Reston:AIAA, 2001. |
| [8] | Anthony S. Pototzky, Patrick C. Murphy. Roll damping derivatives from generalized lifting-surface theory and wind tunnel forced-oscillation tests[C]//AIAA Sci. Tech., 52nd Aerospace Sciences Meeting. 2014, National Harbor, Maryland. |
| [9] |
Sun Zhiwei, Cheng Zeyin, Bai Junqiang, et al. A high efficient method for computing dynamic derivatives of aircraft based on quasi-steady CFD method[J].
Flight Dynamics, 2010, 28(2):28–30.
(in Chinese) 孙智伟, 程泽荫, 白俊强, 等. 基于准定常的飞行器动导数的高效计算方法[J]. 飞行力学, 2010, 28(2) : 28–30. |
| [10] |
Sun Tao, Gao Zhenghong, Huang Jiangtao. Identify of aircraft dynamic derivatives based on CFD technology and analysis of reduce frequency[J].
Flight Dynamics, 2011, 29(4):15–17.
(in Chinese) 孙涛, 高正红, 黄江涛. 基于CFD的动导数计算与减缩频率影响分析[J]. 飞行力学, 2011, 29(4) : 15–17. |
| [11] |
Guo Dong, Xu Min, Chen Shilu. An effective computation method based on field velocity approach for unsteady flow simulation and obtaining dynamic derivatives[J].
Journal of Northwestern Polytechnical University, 2012, 30(5).
(in Chinese) 郭东, 徐敏, 陈士橹. 基于网格速度法的非定常流场模拟和动导数计算[J]. 西北工业大学学报, 2012, 30(5). |
| [12] |
Mi Baigang, Zhan Hao, Zhu Jun. Calculation of dynamic derivatives for aircraft based on CFD technique[J].
Acta Aerodynamica Sinica, 2014, 32(6):834–838.
(in Chinese) 米百刚, 詹浩, 朱军. 基于CFD数值仿真技术的飞行器动导数计算[J]. 空气动力学学报, 2014, 32(6) : 834–838. |
| [13] | Koga S, Hidaka A, Tagai R, et al. Dynamic stability testing of a reentry lifting capsule in a transonic wind tunnel[C]//52nd Aerospace Sciences Meeting, 2014. doi:10.2514/6.2014-1119 |
| [14] |
Liu Xu, Liu Wei, Zhou Yunlong, et al. Numerical simulation of dynamic derivatives for air breathing hypersonic vehicle[J].
Acta Aerodynamica Sinica, 2015, 33(2):147–155.
(in Chinese) 刘绪, 刘伟, 周云龙, 等. 吸气式内外流一体化飞行器动导数数值模拟[J]. 空气动力学学报, 2015, 33(2) : 147–155. |
| [15] |
Xie Lijun, Yang Yunjun, Liu Zhou, et al. A high efficient method for computing danamic derivatives of aircraft based on time spectral method[J].
Acta Aeronautica et Astronautica Sinica, 2015, 36(6):2016–2016.
(in Chinese) 谢立军, 杨云军, 刘周, 等. 基于时间谱方法的飞行器动导数高效计算技术[J]. 航空学报, 2015, 36(6) : 2016–2016. |
| [16] |
Yang Enxia, Kong Fankai, Diao Yanfei. Bracing system for dynamic derivative of large attack angle[J].
Journal of Harbin Engineering University, 2002, 23(5):71–73.
(in Chinese) 杨恩霞, 孔凡凯, 刁彦飞. 大攻角动导数支撑系统的设计与研究[J]. 哈尔滨工程大学学报, 2002, 23(5) : 71–73. |
| [17] |
Huang Da, Zheng Sui, Wen Lihong, et al. Investigation on contain of the large amplitude test to the general dynamic derivative test[J].
Acta Aerodynamica Sinica, 2008, 26(1):111–114.
(in Chinese) 黄达, 郑遂, 文礼红, 等. 大振幅实验对常规动导数实验包容性研究[J]. 空气动力学学报, 2008, 26(1) : 111–114. |
| [18] |
Wang Xinke, Zhang Rui, Ju Bo, et al. Wind tunnel dynamic derivative pitching vibration test device design[J].
Ordnance Industry Automation, 2014, 33(8):72–74.
(in Chinese) 王新科, 张锐, 鞠波, 等. 风洞动导数俯仰振动试验装置的设计[J]. 兵工自动化, 2014, 33(8) : 72–74. |


