飞机及发动机结冰是危及飞行安全的严重问题,与结冰有关的飞行事故每年都有发生。当飞机穿越含有过冷水滴的云层时,过冷水滴撞击到飞机机翼以及发动机的进气部件表面,极易发生冻结。飞机及发动机部件结冰会改变部件的气动性能,对飞机造成极大的安全隐患。融化的冰如果被发动机吸入,会导致发动机叶片的机械损伤,引起发动机熄火停车,造成致命后果。
飞机结冰和防冰过程涉及了复杂的多相流动换热过程,其撞击水滴冻结过程的数学模型至今仍不完善。有关飞机结冰和防冰过程中大水滴撞击、水膜的流动与换热、结冰引起的表面粗糙度对流动换热的影响等研究工作在近年来得到了研究人员的广泛关注[1-6]。过冷水滴撞击特性是飞机结冰和防冰分析的基础。通常,直径小于50 μm的过冷水滴不考虑其在运动及撞击过程中的变形,在撞击机翼表面后不发生飞溅脱离现象。对于小水滴在机翼表面的撞击可以较为准确地采用拉格朗日方法和欧拉方法做出预测[7-8]。而直径大于50 μm的过冷水滴通常称为过冷大水滴(Supercooled Large Droplets, SLD)。大水滴在撞击飞机迎风表面后,会发生飞溅、反弹、二次撞击等多种情况。大水滴的破碎和飞溅会使得撞击水滴的直径和部件表面的水收集系数发生变化,从而影响部件表面生成的冰型。对于飞机结冰分析中大水滴的撞击特性,目前主要还是采用实验数据总结的经验模型进行计算分析[9-10]。由于SLD撞击特性的复杂性,目前还没有一个经验模型在各种结冰条件下都可以给出满意的撞击特性预测结果。因而对SLD撞击过程的机理研究还是非常迫切且必要的。
高速摄像技术的出现为大液滴撞击表面的实验研究提供了强有力的支持。近年来许多研究人员利用高速摄像技术和液滴生成装置研究了液滴撞击形态的变化。Thoroddsen等[11]、Yarin等[12]通过实验方法拍摄了液滴撞击壁面后的铺展、快速溅射、冠状溅射、收缩溅射、部分回弹、完全反弹等多种结果。Rioboo等[13]着重研究了壁面浸润性及表面张力对液滴撞击壁面铺展的影响。Pan等[14]研究了不同属性的液滴撞击不同粗糙度的固体表面的飞溅情况,通过高速摄像装置拍摄了大韦伯数(We数)液滴撞击壁面发生放射状飞溅和日冕皇冠状飞溅,发现当韦伯数足够大时即使在光滑壁面上也能发生液滴飞溅。Tsai等[15]实验研究了微纳米超疏水表面对液滴撞击的影响。液滴撞击的实验研究也具有很大的局限性,通过高速摄像只能得到不同时刻的液滴撞击的形态图片,液滴撞击过程中的速度分布、压力分布、换热情况等均不能测出。同时由于高速液滴撞击实验条件实现困难,目前大量进行的液滴撞击试验的初始速度一般小于40m/s。
理论研究方面,Naber和Reitz[16]在类比射流喷射的基础上考虑了液滴破裂、液滴碰撞、液滴融合以及空气涡流,提出了著名的N-R模型,认为韦伯数决定了液滴碰壁后形态变化。Rioboo等[17]定义了液滴撞击壁面后的几种不同状态:沉积、回弹、部分回弹、迅速飞溅、冠状飞溅、收缩破裂。Cossali等[18-19]、Pan和Law[20]、Pan等[21]通过大量实验及数据分析确定了液滴撞击湿表面不同形态结果的临界韦伯数。数值模拟方面,Gunjal等[22]使用VOF (Volume of Fluid)方法模拟了液滴撞击壁面的过程,并通过实验验证了VOF模型模拟液滴撞击壁面结果的可行性。Kim等[23]使用VOF模型数值模拟了不同速度、流变参数、表面张力条件下的液滴撞击壁面,结果表明液滴的铺展形态取决于雷诺数和韦伯数,液滴的收缩形态决定于毛细数、Bingham-Capillary数,并预测了液滴撞击壁面的最大铺展半径。Bussmann等[24]使用三维模型研究了液滴撞击不对称表面过程中的动态壁面接触角的影响,在模拟液滴撞击倾斜壁面时使用了实验测得的液滴铺展动态壁面接触角作为壁面边界条件,与实验结果较为符合,并在此基础上提出了一种新的给定动态接触角的方法。梁超[25]使用三维模型和VOF方法研究了液滴低速撞击等温壁面过程中的壁面接触角、液滴初始速度、表面张力系数、液滴动力粘度等的影响及液滴撞击热壁面的换热特性,此外还使用二维轴对称模型模拟了不同液滴初始速度、表面张力系数、液滴动力粘度、初始液膜厚度等条件下的液滴撞击液膜过程。贾小娟[26]使用三维模型完成了双液滴垂直及斜向撞击液膜的数值研究。Burtnett[27]使用二维轴对称模型模拟了50 μm液滴撞击微结构表面,对于干表面和渗透表面得到了不同的液滴撞击结果。Tan等[28]采用大水滴破碎、飞溅、反弹模型进行了结冰翼型表面的水滴撞击特性计算,并与试验结果进行了对比验证。
针对飞机结冰所涉及的SLD直径范围内的水滴高速撞击壁面和液膜的研究较少。本文借助VOF方法开展了大水滴撞击壁面过程的动态数值模拟研究,分析了大水滴撞击过程中形态变化、飞溅现象以及撞击特性,数值模拟结果加深了对飞机表面过冷大水滴撞击过程物理机理的理解。
1 计算模型 1.1 计算模型结冰云层中SLD直径分布大致在50 μm到500 μm的范围内。大水滴撞击飞机表面后会发生飞溅、反弹、二次撞击、铺展-收缩-振荡等多种情况。当飞机表面聚集的水滴足够多时,水滴会在飞机表面形成一层液膜,随后还会发生大水滴撞击薄液膜的情况。
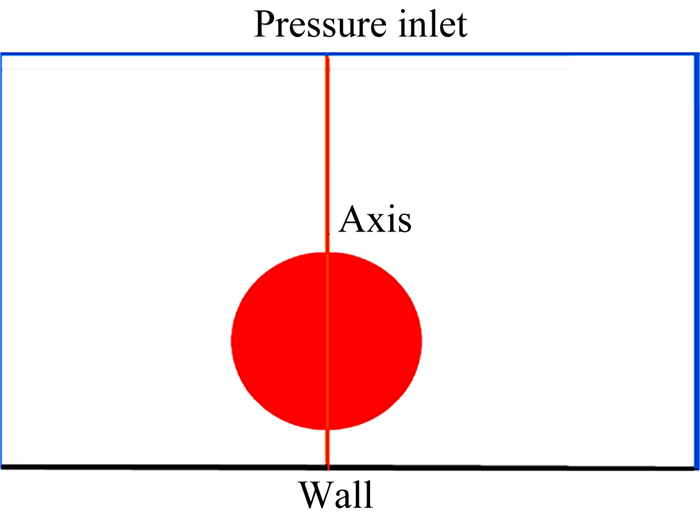
数值模拟中采用二维轴对称模型,计算区域为矩形区域,中间为对称轴,底面为壁面边界条件。对于大水滴高速撞击壁面的数值模拟,为了能够细致地计算出水滴的形态变化,要求计算区域的网格足够密集,使用二维轴对称模型能有效地减小网格数量,缩短计算时间。水滴撞击表面的几何模型如图 1所示。
|
| 图 1 水滴撞击壁面的几何模型 Fig. 1 Geometric model of droplet impingement |
在数值模拟中采用的二维轴对称模型,考虑了一些流体流动过程中的三维效应,能在一定程度上代替三维网格。在水滴低速撞击的很多文献中均使用二维轴对称模型模拟三维的液滴撞击壁面和液滴撞击液膜。相对于三维模型,二维轴对称模型认为流动过程中只存在沿径向的梯度,沿周向均匀分布,因此二维轴对称模型不能够完整捕捉液滴撞击壁面过程中出现的沿周向不均匀、不连续的现象。但使用二维轴对称网格模拟液滴撞击壁面,计算得到的液滴的铺展系数、液膜厚度等数据可信度高,同时能够捕捉到液滴铺展和收缩过程中的二次液滴飞溅、液膜断裂等现象。
1.2 VOF模型大水滴高速撞击壁面的数值模拟,是一种水-空气的两相流动分析。数值追踪两相流界面的方法包括Level-Set方法、粒子标记方法、VOF方法等。其中VOF方法相对于其他的界面追踪方法模型简单,追踪界面精确,能够考虑界面融合和分离现象[29]。
Hirt和Nichols[30]提出的VOF方法,计算中通过引入流体体积分数α来标记界面两边不同相的流体,动态追踪不同相的区域,采用界面重构技术来确定相界面。若假设计算域中共有n相流体,对于任意计算网格的第k相流体来说,其体积分数可能存在如下三种情况,即:
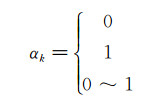
|
(1) |
如果αk等于0,说明在这个网格内不含有第k相流体;如果等于1则说明在这个网格内只存在第k相流体;而如果αk处于0和1之间,表明这个网格内部同时存在多相流体。由于VOF模型假定多相流体不能混合,可以认为该网格处于多相流体界面或流体界面附近。根据体积分数的定义,在同一个网格内部,各相流体的体积分数和应该为1,即:
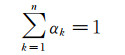
|
(2) |
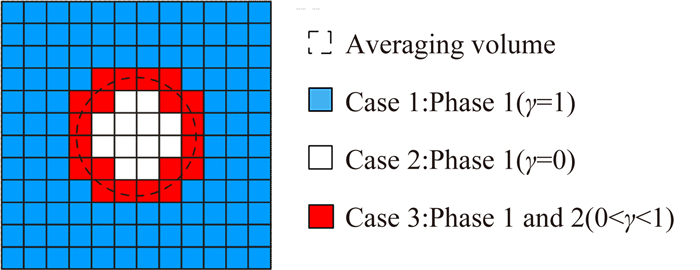
VOF方法在每一个网格内采用体平均来计算流动方程并通过流体体积分数捕捉相的界面,图 2为VOF界面追踪示意图。
|
| 图 2 VOF界面追踪示意图 Fig. 2 Interface tracking diagram of VOF method |
在本文讨论范围内,所涉及的流体相只包含空气相和水滴相两相,在每个计算网格中,第k相(k=1,2)的连续性方程可表示如下:
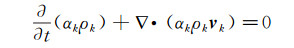
|
(3) |
在VOF模型中,认为在相同位置处的不同相流体具有同样的速度,因此对于空气相和水滴相采用同一套动量方程进行求解:
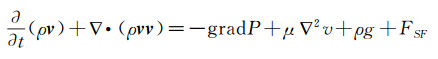
|
(4) |
其中,P为压力,FSF为由表面张力引起的动量源项。式(4)中的物性参数ρ和μ采用体积加权平均法获得:
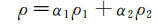
|
(5) |
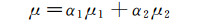
|
(6) |
表面张力采用连续表面张力CSF(Continue Surface Force)模型,CSF模型将VOF计算中附加的表面张力处理为动量方程的源项。相界面两侧的内外压差等于表面曲率和与表面张力系数之积:
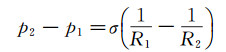
|
(7) |
式中,p1和p2分别为界面两侧的流体压力,R1和R2为两个主曲率半径。
在水滴撞击的过程中表面张力以及壁面浸润性起着重要作用,正是由于表面张力的存在,水滴在撞击壁面达到最大铺展直径后会发生收缩反弹、收缩振荡或者液膜在表面张力作用下拉裂等现象。由于水滴撞击过程中的动态接触角难以测得,数值模拟中使用静态接触角代替动态接触角。
水滴撞击壁面是一个瞬态不可压缩过程,数值模拟采用PISO算法。时间步长和空间步长的选取对于水滴撞击特性的数值模拟非常重要,合适的空间步长和时间步长能够用较少的时间得到精确的结果。空间步长的选取通过网格无关性验证来确定。时间步长通过克朗数确定:
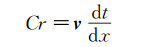
|
(8) |
其中:dt为时间步长;dx为空间步长;Cr可以理解为内扩散相在单位时间内前进的距离与空间步长的比值,这里Cr取为0.25确定初始时间步长。
2 计算方法模型验证结冰云层过冷大水滴直径为几十到几百微米,水滴撞击速度很大,要保证计算过程中合适的Cr,需要的网格步长很小。如果选择的网格较小,虽然能够更精确、细致地计算出大水滴撞击壁面后的形态变化,但是整个网格的数量将急剧增大,同时需要设定较小的时间步长,这样整个模拟的时间将大大增长;如果选择的网格步长过大,则不能精确地计算水滴撞击壁面后的形态变化,计算结果偏差较大,相的界面不清晰。
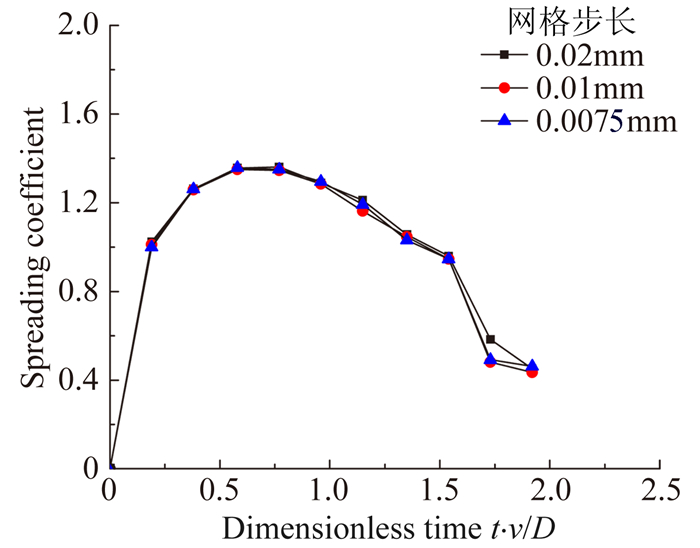
大水滴高速撞击的试验数据很少,因此这里以水滴速度较低的试验数据进行了计算方法的验证。选取试验条件水滴直径2.6mm,水滴初始速度0.5m/s,壁面接触角为160°作为对比算例。图 3为不同网格尺度下不同时刻水滴撞击壁面后的相图。图 4为撞击区域网格尺度分别为0.02mm、0.01mm、0.0075mm条件下水滴在壁面上的铺展系数(d/D)随无量纲时间(t · v/D)的变化曲线,其中d为水滴的铺展直径,D为水滴的初始直径。通过对比发现,相同时刻0.01mm与0.0075mm网格的水相形态和水滴铺展系数基本相同,而与0.02mm网格步长下的水滴形态差异相对较大。在本算例中,0.01mm是一个合适的网格步长,既能保证计算结果的精度,也能保证计算的速度,后面的模拟计算以此网格尺度所对应的无量纲网格尺度作为网格划分的参考依据。

|
| 图 3 0.02mm、0.01mm、0.0075mm网格下的相图(时间间隔为1ms) Fig. 3 Comparison of droplet phase at grids of 0.02mm, 0.01mm, and 0.0075mm(Δt=1ms) |
|
| 图 4 0.02mm、0.01mm、0.0075mm网格步长下的铺展系数变化曲线 Fig. 4 Spread coefficient curves at grids of 0.02mm, 0.01mm, and 0.0075mm |
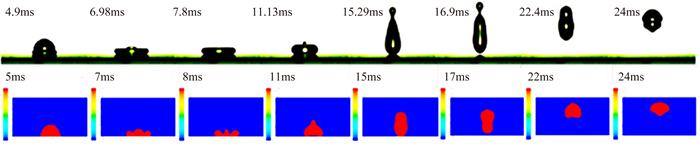
图 5为数值模拟得到的相同时刻水滴撞击壁面后的相图与文献[31]相同时刻实验拍摄图片的对比图。通过对比发现,数值模拟得到的结果与文献中实验得到的结果基本相同,验证了本文计算方法的可靠性。
|
| 图 5 水滴以0.5m/s速度撞击接触角为160°壁面的计算结果与文献中实验结果的对比图 Fig. 5 Numerical simulation results compared with experimental results when a droplet impacts on surface at the velocity of 0.5m/s |
3 计算结果及分析
数值模拟中大水滴直径D选取500 μm、300 μm、100 μm和50 μm,水滴初始速度v0选取30m/s、40m/s、50m/s、60m/s、70m/s。以铝合金材料表面模拟飞机部件表面,壁面接触角为75°。
3.1 大水滴直径对撞击特性的影响研究在高速情况下不同直径的水滴撞击壁面特性时,保持水滴的初始速度为60m/s。观察不同直径下水滴撞击壁面后的形态变化,分析水滴撞击壁面后的铺展系数及铺展时间。
以250网格/直径的网格模拟500 μm水滴撞击壁面的动态过程,确定了水滴的最大铺展半径大约为2mm,因此取模型计算区域为3mm×3mm的对称区域。由于使用该网格步长/直径模拟时,铺展液膜最薄处仅有2层网格的厚度。为了更精确地反映高速水滴撞击壁面过程,对计算区域近壁面处进行了局部加密处理,使用400网格/直径并采用渐密网格。贴近壁面的第一层网格高为0.1 μm,网格高度方向尺度增长率为1.01。
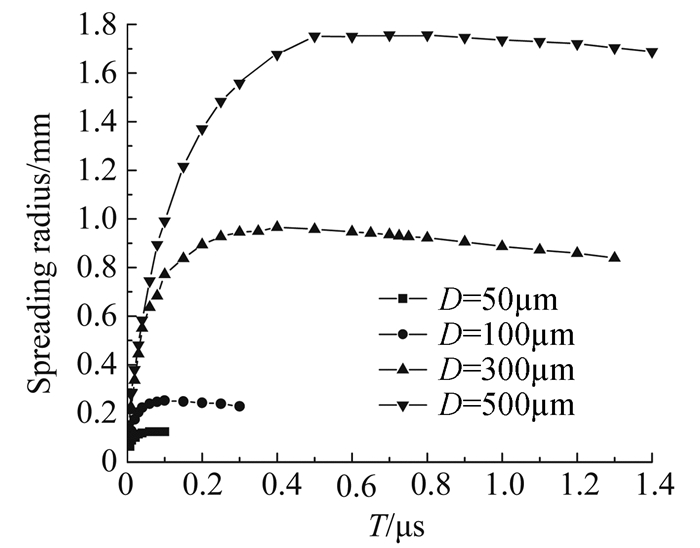
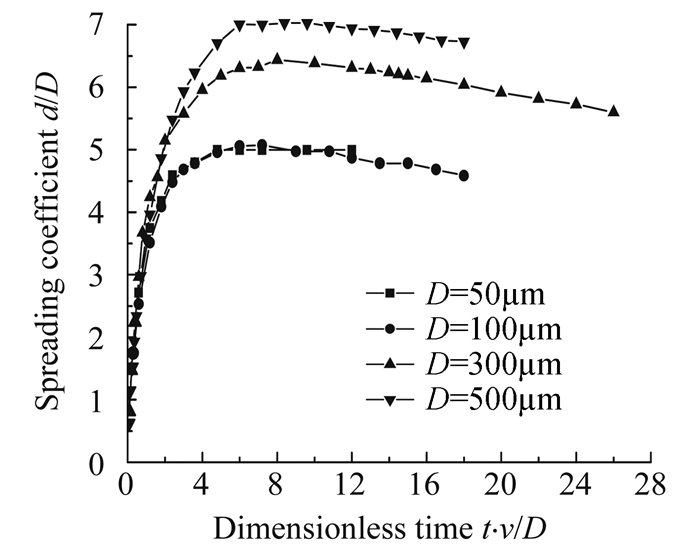
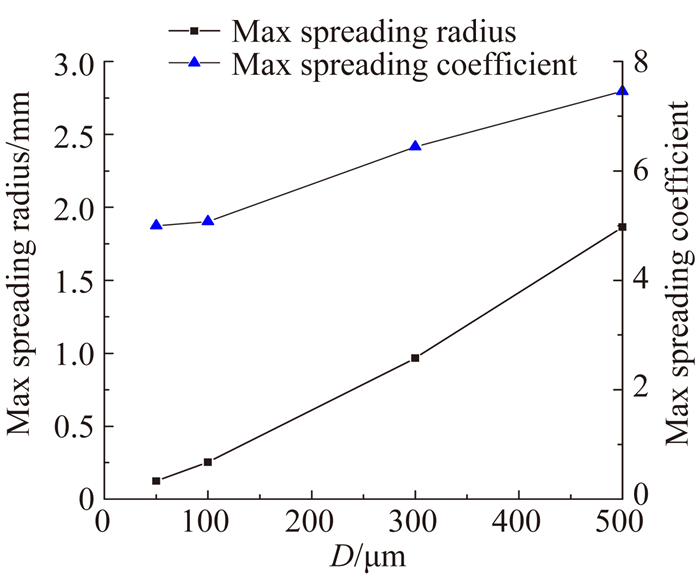
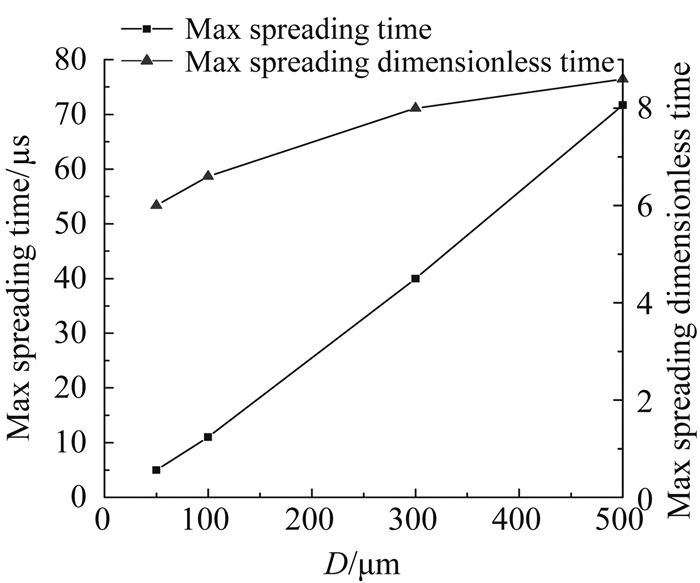
图 6为水滴以不同直径撞击壁面的铺展半径随时间变化曲线。图 7为水滴以不同直径撞击壁面的铺展系数随无量纲时间变化曲线。图 8为水滴直径与最大铺展半径及最大铺展系数关系曲线。图 9为水滴直径与达到最大铺展对应时间的关系曲线。分析图 6~图 9可以看出:大水滴高速撞击壁面时,随着大水滴直径的增大,同一时刻水滴的铺展半径和铺展系数都增大,水滴达到最大铺展对应的时间增大,对应的无量纲时间增大。
|
| 图 6 高速水滴以不同直径撞击壁面的铺展半径随时间变化曲线 Fig. 6 Spreading radius curves of high velocity droplet impacting on surface at different time |
|
| 图 7 不同直径撞击壁面的铺展系数随无量纲时间变化曲线 Fig. 7 Spreading coefficient curves of droplet impacting on surface at different dimensionless time |
|
| 图 8 水滴直径与最大铺展半径及最大铺展系数关系曲线 Fig. 8 Maximum spreading radius curve and maximum spreading coefficient curve varied with droplet diameters |
|
| 图 9 水滴直径与达到最大铺展对应时间关系曲线 Fig. 9 Time-diameter curve and dimensionless time-diameter curve when the droplet reaches the maximum spreading radius |
数值计算分析发现:大水滴以高速撞击壁面时,水滴在壁面上的铺展系数较大,中心液膜的厚度极薄,一般小于10 μm;水滴直径小于300 μm时,液膜的收缩阶段会发生液膜破裂;随着水滴直径的增大,在最大铺展时刻对应的液膜厚度增大,水滴铺展阶段伴随有部分水滴飞溅,飞溅的水滴直径小于50 μm。当水滴初始直径为500 μm时,水滴在壁面上快速铺展,在铺展过程中有发生飞溅现象。由于撞击的初始速度高,水滴铺展系数大,达到最大铺展系数时刻液膜的厚度只有7 μm。在表面张力的作用下,整个薄液膜逐渐收缩,但在收缩阶段并没有发生液膜拉断的情况。随着水滴初始直径的缩小,水滴撞击铺展后的液膜厚度逐渐减小。在直径为300 μm条件下,铺展过程伴随飞溅现象,由于达到最大铺展系数时刻液膜较薄,在表面张力的作用下,收缩阶段发生中心液膜拉断现象;由于被拉断的中心液膜面积较小,表面张力的回复作用不明显,水滴形态变化所储存的能量较少,表面张力在液膜收缩为中心小水滴过程中做功较少,中心液膜收缩形成的中心水滴具备的动能较低,中心水滴没有脱离壁面发生反弹,而是在壁面上不断振荡。在水滴直径为100 μm和50 μm条件下,由于铺展的液膜厚度太薄,表面张力的作用更加剧烈,整个液膜被拉断为多个部分,同时在表面张力的强烈收缩作用下,破裂液膜收缩形成的水滴伴随有飞溅和反弹脱离壁面的情况。由上述分析可知,在水滴撞击壁面达到最大铺展后,水滴的形态变化达到最大,同时水滴的表面张力达到最大,薄液膜开始收缩。如果水滴铺展形成的液膜厚度达到临界值,在较大的表面张力作用下,液膜会被拉断形成外围的液环和中心的液膜;在极端情况下,整个液膜会形成多个外层液环甚至整个液膜被完全拉断为不规则的多个部分(完全破碎)。表 1给出了不同直径大水滴撞击壁面的液膜厚度及飞溅、破裂情况。
| D0/μm | 最大铺展时刻液膜厚/μm | 水滴飞溅及水膜破裂状况 |
| 50 | 2.4 | 收缩阶段水膜破裂,破裂水滴直径10μm。 |
| 100 | 3.8 | 铺展阶段部分飞溅,飞溅水滴直径7μm;收缩阶段水膜破裂,破裂水滴直径10~30μm。 |
| 300 | 4.1 | 铺展阶段部分飞溅,飞溅水滴直径10~16μm;收缩阶段中心水膜拉断,中心水滴直径45μm。 |
| 500 | 7.1 | 铺展阶段存在飞溅,飞溅水滴直径10~30μm;收缩阶段水膜不破裂。 |
3.2 大水滴速度对撞击特性的影响
研究大水滴以不同速度撞击壁面的特性时,保持水滴的直径为300 μm,大水滴以初始速度分别为30m/s、40m/s、50m/s、60m/s、70m/s。观察不同初始速度的大水滴撞击壁面后的形态变化,分析不同时刻水滴的铺展半径及飞溅现象。
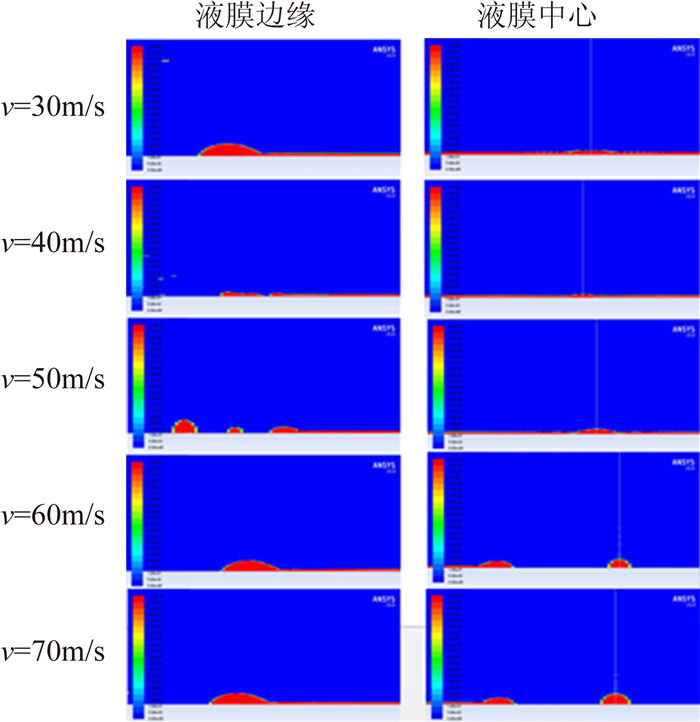
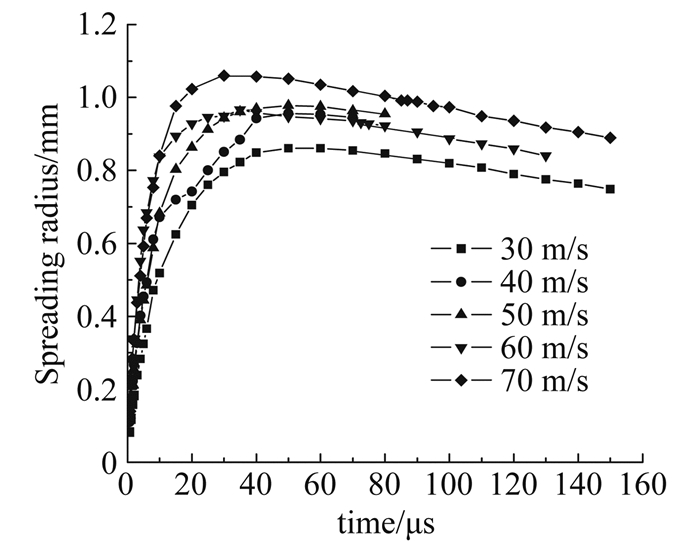
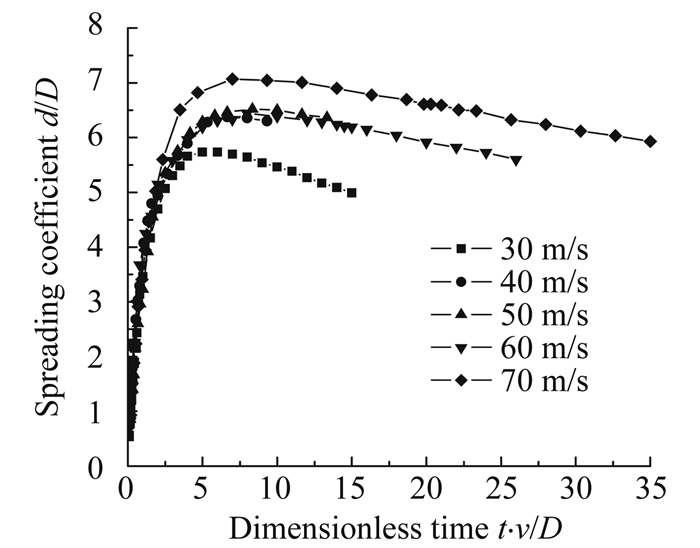
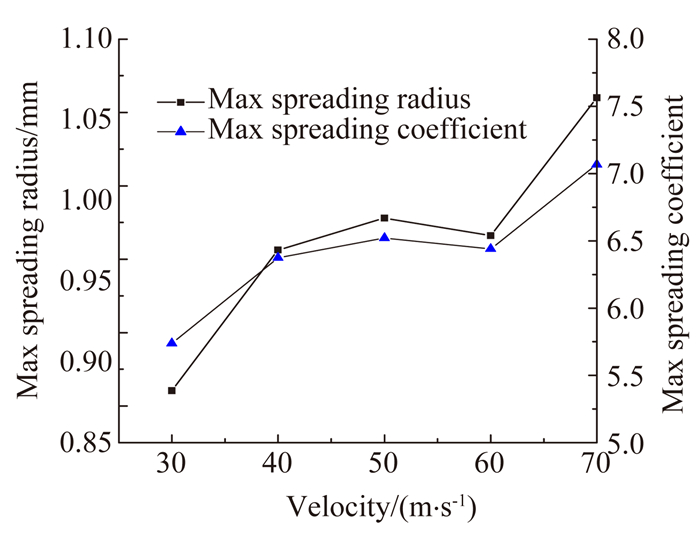
图 10为不同速度下大水滴撞击壁面后的局部放大相图。图 11为不同速度的大水滴撞击壁面后的铺展半径随时间的变化曲线。图 12为不同速度的大水滴撞击壁面后的铺展系数随无量纲时间的变化曲线。图 13为大水滴撞击速度与最大铺展半径及最大铺展系数关系曲线,图 14为大水滴撞击速度与达到最大铺展时间和达到最大铺展对应无量纲时间的关系曲线。从图 11~图 14可以看出:大水滴高速撞击壁面时,随着大水滴初始撞击速度的增大,同一时刻水滴的铺展半径和铺展系数同时增大,水滴的最大铺展半径也增大,水滴达到最大铺展对应的时间缩小,尽管水滴达到最大铺展对应的无量纲时间相差不大,但达到最大铺展时刻对应的液膜厚度减小。
|
| 图 10 不同速度下大水滴撞击壁面后的局部放大相图 Fig. 10 Enlarged pictures of droplet impacting on surface at different velocities |
|
| 图 11 不同速度的大水滴撞击壁面后的铺展半径随时间的变化曲线 Fig. 11 Spreading radius curves of droplet impacting on surface at different velocities |
|
| 图 12 不同速度水滴撞击壁面的铺展系数随无量纲时间的变化曲线 Fig. 12 Spreading coefficient curves of droplet impacting on surface at different velocities |
|
| 图 13 大水滴撞击速度与最大铺展半径及最大铺展系数关系曲线 Fig. 13 Maximum spreading radius and maximum spreading coefficient varied with droplet velocities |
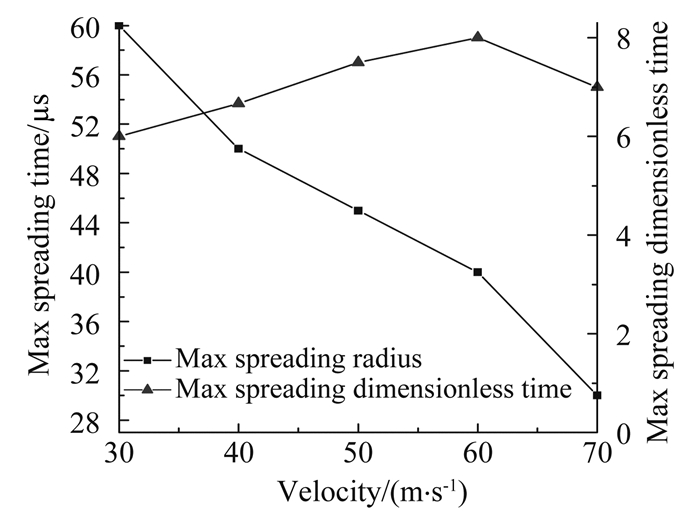
|
| 图 14 大水滴达到最大铺展半径时对应的时间及无量纲时间 Fig. 14 Time-velocity curve and dimensionless time-velocity curve when the impacting droplet reaches the maximum spreading radius |
表 2给出了不同速度的大水滴撞击壁面后的液膜厚度及飞溅情况。初始速度为30m/s的水滴具备的能量相对较低,撞击壁面形成的液膜铺展半径较小,在液膜收缩阶段不发生液膜断裂;初始速度为40m/s和50m/s的水滴具备的能量较高,液膜的铺展半径更大同时更不稳定,在液膜的收缩阶段,边缘液环与中心薄液膜连接处断裂,初始速度为50m/s的初始水滴形成的液膜更是断裂为三部分;初始速度为60m/s和70m/s的水滴能量更高,在薄液膜的中心部位发生了液膜断裂情况,中心液膜断裂并聚集为一个小水滴不断振荡。这是因为:在表面张力的作用下,水滴撞击壁面的收缩阶段,水滴形成的液膜有向液膜中心收拢的趋势。由于液膜边缘处表面张力的作用最为强烈,液膜边缘部分的水相率先向内运动,而液膜中心部位的水相运动趋势不明显,中心部位的液膜厚度基本不发生变化。边缘液膜运动的结果是液膜的铺展半径变小,同时在液膜边缘处水相堆积形成凸状液环。
| 初始速度v/(m·s-1) | 最大铺展时刻液膜厚/μm | 水滴飞溅及水膜破裂状况 |
| 30 | 7 | 飞溅液滴直径10~20μm; 收缩阶段水膜不破裂。 |
| 40 | 6.6 | 飞溅液滴直径10μm左右;收缩阶段边缘液膜拉断。 |
| 50 | 4.7 | 飞溅液滴直径10μm左右;收缩阶段边缘液膜拉断。 |
| 60 | 4.1 | 飞溅水滴直径10μm左右;收缩阶段中心水膜拉断,中心液滴45μm。 |
| 70 | 3.4 | 飞溅液滴直径10μm左右;收缩阶段中心液膜拉断,中心液滴48μm。 |
4 结论
使用VOF方法数值模拟了直径50~500 μm范围内的大水滴以高速撞击壁面的撞击特性。通过改变大水滴的直径和大水滴的初始速度,计算分析了不同条件下大水滴形态变化、撞击结果以及铺展系数的变化。
1) 直径50~500 μm的大水滴以高速撞击壁面时,水滴在壁面上的最大铺展系数较大,达到最大铺展后的液膜厚度界于1~10 μm之间。由于液膜的厚度很薄,在表面张力的作用下,可能发生液膜被拉断的行为。
2) 随着水滴直径以及撞击速度的增大,水滴的铺展速度、最大铺展半径、最大铺展系数均增大。水滴直径增大时,水滴达到最大铺展所用的时间变长,所用的无量纲时间呈微弱增大趋势;同一直径水滴初始速度增大时,水滴达到最大铺展所用的时间减少,所用的无量纲时间变化相对较小。
3) 低速情况下水滴撞击光滑壁面不易发生飞溅现象,但在水滴高速撞击光滑壁面的大韦伯数情况下,数值模拟发现了明显的飞溅现象。
致谢: 数值计算分析过程中得到了上海交通大学机械与动力工程学院工程热物理研究所陈勇老师的支持和帮助,这里对其帮助表示感谢。| [1] | Wright W B. Further refinement of the LEWICE SLD model. AIAA 2006-0464[R]. Reston:AIAA, 2006. |
| [2] | Honsek R, Habashi W G, Aube M S. Eulerian modeling of in-flight icing due to supercooled large droplets[J]. Journal of Aircraft, 2008, 45(4):1290–1296. DOI:10.2514/1.34541 |
| [3] | Rothmayer A P, Hu H. Solutions for two-dimensional instabilities of ice surfaces uniformly wetted by thin films. AIAA 2012-3133[R]. Reston:AIAA, 2012. |
| [4] | Zhang K, Blake J, Rothmayer A, et al. An experimental investigation on wind-driven rivulet/film flows over a NACA0012 airfoil by using digital image projection technique. AIAA 2014-0741[R]. Reston:AIAA, 2014. |
| [5] | Dong W, Zheng M, Zhu J, et al. Calculation and analysis of water film flow characteristics on anti-icing airfoil surface. AIAA 2015-0538[R]. Reston:AIAA, 2015. |
| [6] | Reulet P, Aupoix B, Donjat D, et al. Boundary layer and heat transfer characterization on a flat plate with realistic ice roughness[R]. SAE Technical 2015-01-2096. |
| [7] | 易贤.飞机积冰的数值计算与积冰试验相似准则研究[D].绵阳:中国空气动力研究与发展中心, 2007. |
| [8] | Dong W, Zhu J, Zhou Z, et al. Heat transfer and temperature analysis of an aero-engine strut under icing conditions[J]. Journal of Aircraft, 2014, 52(1):216–225. |
| [9] | Wright W B, Potapczuk M G. Semi-empirical modeling of SLD physics. AIAA 2004-412[R]. Reston:AIAA, 2004. |
| [10] | Rutkowski A, Wright W, Potapczuk M. Numerical study of droplet splashing and re-impingement. AIAA 2003-388[R]. Reston:AIAA, 2003. |
| [11] | Thoroddsen S T, Etoh T G, Takehara K. High speed imaging of drops and bubbles[J]. Annual Review of Fluid Mechanics, 2008, 40:257–285. DOI:10.1146/annurev.fluid.40.111406.102215 |
| [12] | Yarin A L. Drop impact dynamics:Splashing, Spreading, Receding, Bouncing[J]. Annual Review of Fluid Mechanics, 2006, 38(1):159. DOI:10.1146/annurev.fluid.38.050304.092144 |
| [13] | Rioboo R, Marengo M, Tropea C. Time evolution of liquid drop impact onto solid, dry surfaces[J]. Experiments in Fluids, 2002, 33(1):112–124. DOI:10.1007/s00348-002-0431-x |
| [14] | Pan K, Tseng K, Wang C. Breakup of a droplet at high velocity impacting a solid surface[J]. Experiments in Fluids, 2010, 48(1):143–156. DOI:10.1007/s00348-009-0697-3 |
| [15] | Tsai P, Pacheco S, Pirat C, et al. Drop impact upon micro-and nanostructured superhydrophobic surfaces[J]. Langmuir, 2009, 25(20):12293–12298. DOI:10.1021/la900330q |
| [16] | Naber J, Reitz R. Modeling engine spray/wall impingement[J]. SAE transactions, 1989, 97(6):118–140. |
| [17] | Rioboo R, Tropea C, Marango M. Outcomes from a drop impact on solid surfaces[J]. Atomization Sprays, 2001, 11(2):156–165. |
| [18] | Cossali G E, Coghe A, Marengo M. The impact of a single drop on a wetted solid surface[J]. Exp. in Fluids, 1997, 22(6):463–472. DOI:10.1007/s003480050073 |
| [19] | Cossali G E, Marengo M, Coghe A. The role of time in single drop splash on thin film[J]. Experiments in Fluids, 2004, 36(6):888–900. DOI:10.1007/s00348-003-0772-0 |
| [20] | Pan K L, Law C K. Dynamics of droplet-film collision[J]. Fluid Mesh, 2007, 587(587):1–22. |
| [21] | Pan K L, Cheng K R, Chou P C, et al. Collision dynamics of high-speed droplets upon layers of variable thickness[J]. Experiments in Fluids, 2008, 45(3):435–446. DOI:10.1007/s00348-008-0486-4 |
| [22] | Gunjal P R, Ranade V V, Chaudhari R V. Dynamics of drop impact on solid surface:experiments and VOF simulations[J]. AIChE Journal, 2005, 51(1):59–78. DOI:10.1002/(ISSN)1547-5905 |
| [23] | Kim E, Baek J. Numerical study of the parameters governing the impact dynamics of yield-stress fluid droplets on a solid surface[J]. Journal of Non-Newtonian Fluid Mechanics, 2012, 173-174:62–71. DOI:10.1016/j.jnnfm.2012.02.005 |
| [24] | Bussmann M, Mostaghimi J, Chandra S. On a three-dimensional volume tracking model of droplet impact[J]. Physics of Fluids, 1999, 11(6):1406–1417. DOI:10.1063/1.870005 |
| [25] |
Liang C. Numerical research on dynamic characteristics of micro droplet impact on surface and liquid film[D]. Chongqing:Chongqing University, 2013. (in Chinese) 梁超.微小液滴撞击固体壁面及薄液膜动态特性的数值研究[D].重庆:重庆大学, 2013. http://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201509045.htm |
| [26] |
Jia Xiaojuan. Numerical investigation on flow performance of droplet impinge upon aliquid film[D]. Dalian:Dalian University of Technology, 2012. (in Chinese) 贾小娟.液滴撞击液膜流动特性数值研究[D].大连:大连理工大学, 2012. |
| [27] | Burtnett E N. Volume of fluid simulations for droplet impact on dry and wetted hydrophobic and superhydrophobic surfaces[D]. Mississippi State:Mississippi State University, 2012. http://adsabs.harvard.edu/abs/2012PhDT.......107B |
| [28] | Tan S C, Papadakis M. Droplet breakup, splashing and re-impingement on an iced airfoil. AIAA 2005-5185[R]. Reston:AIAA, 2005. |
| [29] | Gopala V R, Wachem B G M. Volume of fluid methods for immiscible-fluid and free-surface flows[J]. Chemical Engineering Journal, 2008, 141(1-3):204–221. DOI:10.1016/j.cej.2007.12.035 |
| [30] | Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamic of free boundaries[J]. Comp. Physics, 1981, 39(81):201–225. |
| [31] | Mao T, Kuhn D C S, Tran H. Spread and rebound of liquid droplets upon impact on flat surfaces[J]. Aiche. Journal, 1997, 43(9):2169–2179. DOI:10.1002/(ISSN)1547-5905 |



