2. 北京航空航天大学 人机工效与环境控制重点学科实验室, 北京 100191
2. Fundamental Science on Ergonomics and Environment Control Laboratory, Beihang University, Beijing 100191, China
为了验证飞机防冰系统的性能以及各部件的有效性,防冰系统性能的理论分析和试验在飞机适航认证中缺一不可[1]。试验一方面验证理论计算,另一方面直接有力地检验飞机防除冰系统及其部件的有效性,而理论计算可用于任意条件下的防冰系统性能分析。自然结冰条件下的飞行试验是适航中必不可少的一个步骤,但风险性很高。因此在自然结冰飞行试验之前一般都要进行理论分析和计算,还要在冰风洞内或非结冰气象条件下开展防除冰系统性能试验,以初步地检验防除冰系统的性能。非结冰气象条件下防冰系统的理论计算为其在自然结冰条件下的理论计算提供依据。国内较少开展飞机防冰系统在非结冰气象条件下的数值模拟[2-3],也未曾得到试验验证,因此开展这方面的研究具有重要的意义。
本文以某型飞机为背景,开展了非结冰气象条件下机翼热气防冰系统的数值模拟研究,为此方法扩展到结冰气象条件下防冰系统的模拟提供依据,有助于提高飞机在自然结冰条件下的飞行安全。
1 数值模拟方法欧美国家由于有冰风洞试验数据的支持,已经开发了比较成熟的结/防冰计算软件,例如:美国的LEWICE[4],加拿大的FENSAP-ICE[5]和CANICE[6],英国的TRAJICE2[7],法国的ONERA[8],意大利的CIRAMMIL[9]等。本文采用内外传热耦合的方法进行防冰系统表面温度计算,实现了非结冰气象条件下防冰系统性能的预估。
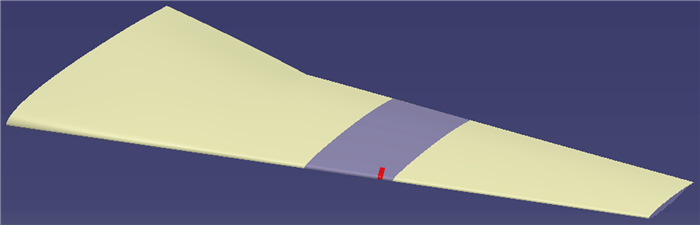
1.1 计算模型外部流场计算选取三维典型机翼的一段,并选取防冰腔某一段进行腔内热气流动与换热计算及防冰表面温度的计算,如图 1所示。选取的机翼段展长1.76m;防冰腔段展向长0.1m,蒙皮厚度1.6mm。
|
| 图 1 机翼及防冰腔计算模型位置 Fig. 1 Positions of the model of the wing and anti-icing cavity for simulation |
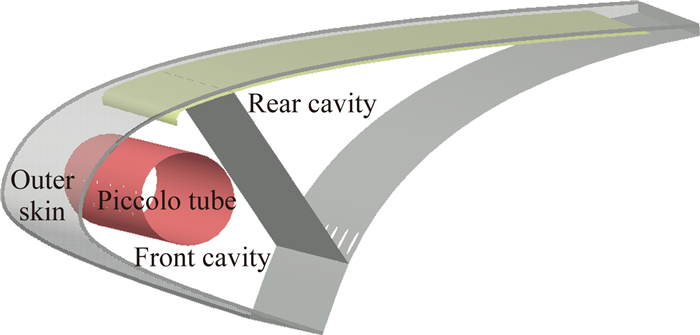
飞机机翼热气防冰系统比较复杂,本文研究的热气防冰系统示意图如图 2所示,是双排阵列笛形管喷口、双蒙皮热气通道结构。发动机引气出来的热气经过管路流到前缘缝翼内的笛形管内,热气从笛形管上的双排交错小孔射流出到前腔,同时加热蒙皮表面,热气经过双蒙皮通道后流到后腔,并从后腔的排气孔排出到环境中。
|
| 图 2 热气防冰腔示意图 Fig. 2 Schematic of hot air anti-icing cavity |
1.2 数值模拟总体思想
机翼热气防冰系统性能评价的重要指标之一是表面温度分布。本文数值模拟的最终目标是得到防冰系统工作时防冰表面温度结果。
热气防冰系统表面温度的计算需要考虑:①防冰腔外部即飞机机翼外部气流对蒙皮产生的换热;②防冰腔内热气对蒙皮产生的换热;③蒙皮本身的导热。简单来说,非结冰气象条件下防冰腔可认为是无相变气-气热交换器;结冰气象条件下防冰腔则是有相变(撞击水蒸发)气-气热交换器。复杂之处在于防冰腔内、外部空气的流动比较复杂,要想准确地预测传热现象比较困难。
防冰表面温度计算步骤如下:
步骤1计算翼身组合体外部流场。
步骤2设置表面温度初始值,计算防冰腔内部流动传热。
步骤3利用附面层积分方法计算外部对流传热系数,并分析外部散热热流。
步骤4将外部热流作为防冰腔外表面热流边界条件,进一步计算蒙皮导热以及防冰腔内部流动与换热,得到新的表面温度。
步骤5重复步骤3和步骤4直到所有控制容积相邻两步的表面温度结果的最大差值小于小量ε。
整个计算基于计算流体力学(CFD)的方法,最终得到非结冰气象条件下防冰腔表面温度结果。
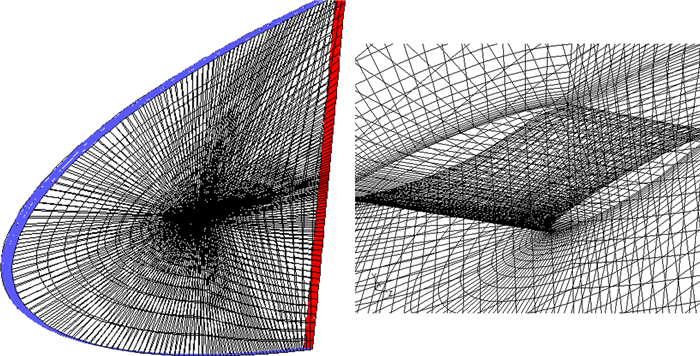
1.3 外部流场计算利用CFD方法计算机翼外部流场,采用Fluent计算工具。图 3给出了外部三维流场计算网格,划分工具采用Gambit软件。网格总数为147900个网格,为结构化的六面体网格。
|
| 图 3 外部流场计算网格 Fig. 3 Grid for external flow field of wing-body combination |
机翼外部流场计算采用压力远场边界条件,无黏流模型。压力修正采用分离式求解方法,即Simple算法。方程组的离散采用二阶迎风格式。外部流场计算收敛后可近似得到机翼附面层外边界处速度,为附面层积分方法计算外部对流传热系数做准备。
监控速度及能量的残差值来检验计算是否收敛。计算收敛后,将空气速度及温度结果导出,作为计算外部对流传热系数的输入条件。
1.4 外部对流传热系数计算外部对流传热系数时,根据机翼表面的空气流动特点,机翼可分成驻点、上表面和下表面,其中:上下表面均有层流区、湍流区和过渡区。本文总结了前人通过理论推导和大量试验得到的各区域的对流传热系数计算公式,采用的是附面层积分方法。
在驻点位置,根据Smith和Spalding经过大量试验后得出的结论,驻点区的对流传热系数计算式为[10]
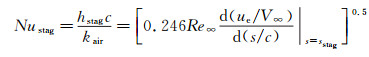
|
(1) |
式中: Nustag为驻点努塞尔数;hstag为驻点对流传热系数;c为机翼弦长;kair为空气导热系数;Re∞=V∞c/vair为基于弦长的远场雷诺数;V∞为远场空气速度;vair为空气运动黏度;ue为附面层外边界处切向方向速度;s为弧长。
层流区域的对流传热计算式为[11]

|
(2) |
式(2)考虑了压力梯度及非等温表面情况。式中:Res=ues/vair为基于弧长的当地雷诺数;Ve为附面层外界处速度;ΔT=Ts-Te为当地表面和附面层外边界处温差。
湍流区域的对流传热系数计算式为[11]
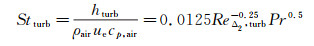
|
(3) |
式中:St为斯坦顿数;ρair为空气密度;cp, air为空气定压比热;ReΔ2, trub=ueΔ2/vair为基于焓厚度的当地雷诺数;Pr为空气普朗特数。ReΔ2, trub可近似为如下积分公式[11]
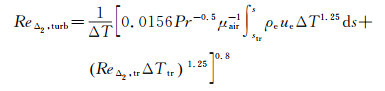
|
(4) |
式中:ReΔ2, tr为转捩起始位置的焓厚度雷诺数,计算表达式为
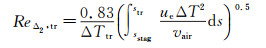
|
(5) |
过渡区域的对流传热系数计算引入间断因子γ(s),代表在弧长s处流动呈现湍流的概率,其表达式为[12]
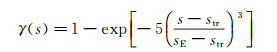
|
(6) |
式中:str为过渡区起始位置距离驻点位置的弧长;sE为过渡区终止位置对应的弧长。那么:
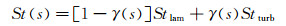
|
(7) |
通过以上积分公式的计算,可得到各区域的对流传热系数。
1.5 内部流场及蒙皮导热初始计算防冰腔内部热气流动与换热比较复杂,将内部热气流动换热及蒙皮导热问题一起考虑,本文利用计算流体力学软件Fluent来开展计算。首先需要将防冰腔内的空间及蒙皮离散化即划分网格。防冰腔曲面数量较多,结构复杂,不利于网格结构化划分,因此对模型进行简化如下:
1) 由于笛形管喷口喷射方向基本垂直于缝翼前缘,因此选择防冰腔段时垂直于前缘缝翼截取。
2) 根据双蒙皮通道位置,对双蒙皮曲面进行切割,构建通道轮廓,将部分小曲面改为平面,例如通道末端铣刀形状导致的小曲面。
3) 忽略双蒙皮通道内蒙皮的厚度。
4) 根据笛形管喷口位置,对笛形管圆柱曲面进行切割,构建与圆形喷口等面积的方形热气喷口,并忽略笛形管管壁厚度。
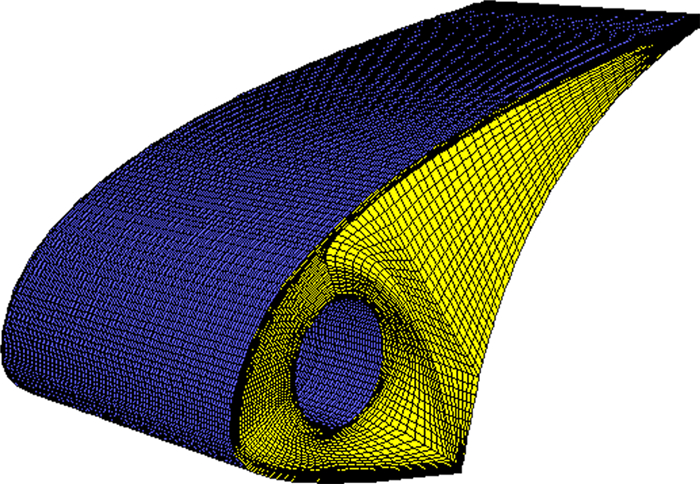
完成以上简化工作后,对模型进行网格划分,采用Gambit网格划分工具。图 4为防冰腔网格,包括蒙皮固体区域网格和流体流动区域网格。由于前腔流动变化剧烈,划分结构化的网格及蒙皮内表面附面层网格有助于提高计算的精度,为了保证前腔结构化网格的生成,前腔进行分区处理。固壁区域的网格数为46104,腔内气体流动区域的网格数为393924。
|
| 图 4 防冰腔内部流场计算网格 Fig. 4 Grid for internal flow field of anti-icing cavity |
防冰腔内热气流动换热以及蒙皮的导热计算需要联立求解热气的N-S方程、能量方程以及固体区域的导热方程。另外,湍流模型采用Spallart-Allmaras一方程模型,比较适合冲击射流曲面的流动计算。采用压力入口、压力出口边界条件,蒙皮外表面采取等温边界条件。
防冰腔内流动变化比较剧烈,特别是在壁面附近,尝试计算后,发现压力的修正采用Coupled算法在计算收敛方面更具优势。方程组的离散采用二阶迎风格式。
1.6 内外传热耦合计算表面温度为了得到蒙皮表面温度,本文将外部热流、内部热流以及蒙皮自身导热三者一起强固耦合计算,有别于结/防冰软件FENSAP-ICE所采用的松散耦合方法[13-14]。本文在计算导热与防冰腔内部流动与换热时,将外部热载荷作为边界条件加载到防冰腔蒙皮外表面,每个迭代步不断地交替更新表面温度和外部热载荷,通过监控相邻迭代步的表面温度变化来判断迭代计算的收敛,最终得到表面平衡温度。
这里将外部流场计算网格简称为外网格;内部流场计算网格简称为内网格;外网格和内网格的重合面称为界面。内外传热耦合计算表面温度存在的难点之一是:如何在界面处给内、外网格相互传递变量值的信息,达到传热耦合求解的目的。
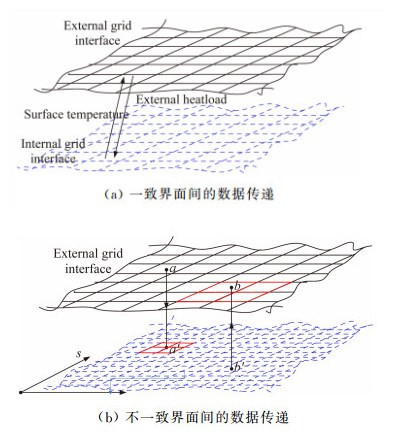
在文献[3]的研究中,外部流场计算区域在机翼展向方向的范围较小,仅为所研究防冰腔的展向长度,外网格和内网格在界面处的面网格一致,因此界面网格处的变量值传递时只需要寻找相同位置的网格即可,如图 5(a)所示,找到相同位置的界面网格后,就可以方便地将计算所得的外网格界面处的热载荷传递给内网格界面,作为计算新的表面温度的输入;将内网格计算所得的表面温度传递给外网格界面,作为计算新的防冰热载荷的输入。
|
| 图 5 内、外网格界面数据传递 Fig. 5 Data transfer between the internal-external grid interfaces |
由于本文外流场计算针对整个机翼进行,计算区域相对较大,若采用上述方法来实现界面的数据传递,外网格的界面网格必然会较密,网格数量的增多将降低计算速度。本文对界面间数据传递方法进行改进,采用了线性插值的方法进行双向插值,实现不一致界面间的数据传递,如图 5(b)所示。这样外网格的界面网格可以疏于内网格的界面网格,大大提高了计算速度。
根据外网格界面网格节点a的坐标找到内网格界面上的4个最近的网格,插值计算得到a′的表面温度,将a′的表面温度结果传递给外网格节点a。根据内网格界面网格节点b′的坐标找到外网格界面上的4个最近的网格,插值计算得到b的防冰热载荷,将b的热载荷结果传递给内网格节点b′。其他界面网格如法炮制,即可完成内、外网格界面间的数据传递。插值计算时根据展向z坐标以及弧长s进行二维线性插值,定义见图 5(b)。
编写子函数来寻找每个界面网格插值计算所需的4个网格,并在表面温度迭代计算之前运行,将网格序号存贮,为每次迭代计算中插值及传递数据使用。
利用上述内外传热耦合思想以及改进后的内、外网格界面数据传递方法,对防冰腔在非结冰气象条件下防冰表面温度开展了计算。
2 数值模拟结果与分析在计算表面对流传热系数时,则根据雷诺数大小来划分层流区、湍流区和过渡区。当雷诺数小于5×105,认为层流区[15];雷诺数大于2×106,认为湍流区[15];雷诺数在以上两者之间为过渡区。
计算状态如表 1所示,表中p为压力,α为迎角,T∞为环境温度,Ma为马赫数。
| p/Pa | α/(°) | T∞/℃ | Ma | |
| Case1 | 75 000 | 3 | 10 | 0.3 |
| Case2 | 65 000 | 3 | 4 | 0.4 |
表 1中状态1和状态2的防冰系统引气状态分别为:压力0.26 MPa,温度200 ℃;压力0.25 MPa,温度200 ℃。蒙皮固体区域导热系数为121W/(m·K)。
图 6和图 7给出了状态1的数值模拟三维云图结果。从防冰腔三维结果中抽取中间截面的温度与对流传热系数结果,如图 8所示。
|
| 图 6 防冰腔外表面对流传热系数三维云图 Fig. 6 Contours plot of the convective heat transfer coefficient of the anti-icing cavity external surface |
|
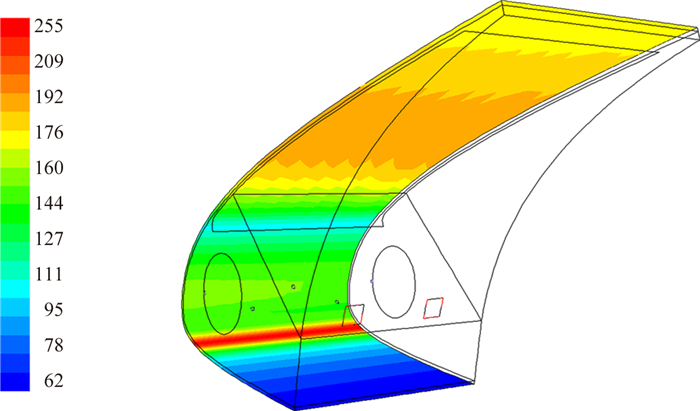
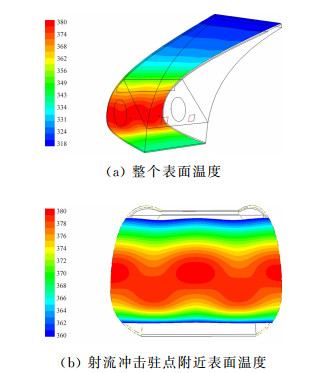
| 图 7 防冰表面温度三维云图(单位:K) Fig. 7 Surface temperature distribution of the anti-icing cavity(unit: K) |
|
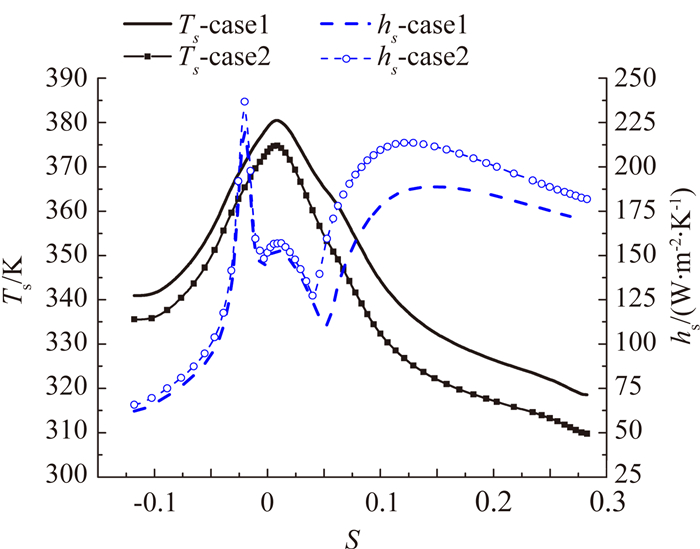
| 图 8 二维截面对流传热系数及表面温度模拟结果 Fig. 8 2D surface heat transfer coefficient and temperature simulation results |
由图 6可以看到,机翼实际驻点处的对流传热系数达到一个峰值;气流在驻点处分流,气流往上表面流动时,对流传热系数沿着气流流动方向首先在层流区逐渐下降,然后在过渡区逐渐升高,完全转变成湍流后对流传热系数又开始下降,这一点从图 8中二维截面的对流传热系数曲线图也可看出;气流往下表面流动时,由于流动速度较低,下表面一直处于层流状态,对流换热系数一直下降。气流往上表面流动时对流传热系数变化并不是一直都平滑,某些地方出现拐点,如图 8中二维截面s=0.1附近,分析发现s=0.1附近也是温度变化的拐点位置,对流传热系数与表面温度有关系,因为表面温度影响着附近空气的物性参数,从而影响对流传热系数。
由图 7可知,射流驻点附近的表面温度明显高于其他部分的温度,呈现出笛形孔交错排列的形状,上下表面温度逐渐降低。从图 8可知状态2的表面温度整体低于状态1的,这主要是因为状态2的环境温度低于状态1,另外还因为飞行速度高于状态1,这样导致对流散热量会高于状态1。对比图 8中状态1和状态2的对流换热系数可看出状态2驻点处hs要高于状态1的,且上表面层流向紊流的转变提前,导致上表面后部状态2的hs要高于状态1。
从本文计算结果来看,在非结冰气象条件下飞行时,此段防冰系统工作时能够使表面温度最高达到380K (107℃)左右,上表面最低达到310K (37℃)左右,下表面最低达到335K (62℃)左右。在结冰气象条件下,由于环境温度低加上撞击水的蒸发效果,表面整体温度会低于非结冰气象条件下的表面温度。但从此处非结冰气象条件下较高的表面温度结果来看,即使在结冰气象条件下,驻点附近以及下表面的温度能够满足防冰要求。因为在结冰气象条件下,上表面结冰相对于下表面结冰对飞机性能的影响要小,且一般来说机翼上表面水滴撞击范围要小于下表面的水滴撞击范围,上表面溢流水极限也会远小于上表面防护范围,因此在上表面后部即使温度低(在结冰气象条件下会远低于此处计算结果37℃),由于没有水的存在不会发生结冰。本文非结冰气象条件下机翼热气防冰系统性能的预测为飞机防冰系统在非结冰气象/结冰气象条件下的性能飞行试验提供了参考依据。
3 结论本文提出并详细介绍了内外传热耦合计算热气防冰系统表面温度的方法。该方法基于Fluent软件进行二次开发,可扩充性较好。
通过改进内外网格数据传递的方法,采用双向线性插值,实现了不一致界面间的数据传递。该方法可减小外流场计算网格,相对以往内外网格在界面网格处须一致的情况,有效地提高了计算速度。
采用该方法对某型飞机某段防冰系统在非结冰气象条件下的表面温度开展计算,结果表明整个防冰表面温度较高。射流驻点附近表面温度明显高于其他部分的温度,分布呈笛型孔交错排列形状。上表面表面温度低于下表面表面温度。
| [1] |
Civil Aviation Administration of China. Civil aviation regulations of China, Part 25:airworthiness standards for transport category airplanes. 4th ed.[S]. Beijing:Civil Aviation Administration of China, 2001:144. (in Chinese) 中国民航总局.中国民用航空规章第25部:运输类飞机适航标准第四次修订版[S].北京:中国民用航空总局, 2011:144. |
| [2] |
Bu Xueqin, Lin Guiping. Predictions of collection efficiency and anti-icing surface temperature[J].
Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(10):1182–1185.
(in Chinese) 卜雪琴, 林贵平. 基于CFD的水收集系数及防冰表面温度预测[J]. 北京航空航天大学, 2007, 33(10) : 1182–1185. |
| [3] |
Bu Xueqin, Lin Guiping, Yu Jia. Three dimensional conjugate heat transfer simulation for the surface temperature of wing hot-air anti-icing system[J].
Journal of Aerospace Power, 2009, 24(11):2495–2500.
(in Chinese) 卜雪琴, 林贵平, 郁嘉. 三维内外热耦合计算热气防冰系统表面温度[J]. 航空动力学报, 2009, 24(11) : 2495–2500. |
| [4] | Wright W B. User manual for the NASA Glenn ice accretion code LEWICE version 2.2.2[R]. NASA CR-2002-211793, 2002. |
| [5] | Morency F, Beaugendre H, Baruzzi G S, et al. FENSAP-ICE:a comprehensive 3D simulation system for in-flight icing. AIAA 2001-2566[R]. Reston:AIAA, 2001. |
| [6] | Saeed F, Paraschivoiu I. Optimization of a hot-air anti-icing system. AIAA 2003-0733[R]. Reston:AIAA, 2003. |
| [7] | Gent R W. TRAJICE2, A combined water droplet and ice accretion prediction program for aerofoil[R]. DRA Technical Report No. TR90054, 1990. |
| [8] | Hedde T, Guffond D. ONERA three-dimensional icing model[J]. AIAA Journal, 1995, 33(6):1038–1045. DOI:10.2514/3.12795 |
| [9] | Fortin G, Perron J, Mingione G, et al. CIRAAMIL ice accretion code improvement. AIAA 2009-3968[R]. Reston:AIAA, 2009. |
| [10] | Smith A G, Spalding D B. Heat transfer in a laminar boundary layer with constant fluid properties and constant wall temperature[J]. Journal of the Royal Aeronautical Society, 1958, 62(1):60–64. |
| [11] | Ambrok G S. Approximate solution of equations for the thermal boundary layer with variations in boundary layer structure[J]. Soviet Physics-Technical Physics, 1957(2):1979–1986. |
| [12] | Abu-Ghannam B, Shaw R. Natural transition of boundary layers——The effects of turbulence, pressure gradient and flow history[J]. Journal of Mechanical Engineering Science, 1980, 22(5):213–228. DOI:10.1243/JMES_JOUR_1980_022_043_02 |
| [13] | Croce G, Habashi W G, Guevremont G, et al. 3D thermal analysis of an anti-icing device using[R]. FENSAP-ICE. AIAA-1998-0193, 1998. |
| [14] | Wang H, Tran P, Habashi W G, et al. Anti-icing simulation in wet air of a piccolo system using FENSAP-ICE[R]. SAE paper 2007-01-3357, 2007. |
| [15] |
Qiu Xiegang, Han Fenghua.
Aircraft anti-icing system[M]. Beijing: Compilation and Examination Group of Aero Specialized Teaching Materials, 1985 : 166 .
(in Chinese) 裘燮纲, 韩凤华. 飞机防冰系统[M]. 北京: 航空专业教材编审组, 1985 : 166 . |



