2. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
飞机在含有过冷水滴的云层中飞行时可能遭遇结冰现象[1-2]。结冰是飞行安全的主要隐患之一,轻则使飞机的安全飞行范围减小,重则导致机毁人亡的严重事故。冰形是结冰对飞机安全影响研究的输入条件,也是防/除冰研究的依据和基础[3]。
冰风洞试验是获得冰形的主要手段之一。冰形将进一步制作成相应的模型,用于常规风洞中冰对气动特性的影响研究[4-5]。冰风洞试验直接得到的结冰形状复杂多样,有的外形极不规则,例如,温度较高、液态水含量较大的情况下的溢流和二次冻结可能导致形成羽状冰形,这种冰的外形极其复杂,很难精确加工成可安装在飞行器表面的冰模[6]。因此,冰风洞中直接得到的复杂冰形必须经过合理的修正和简化处理,才能应用于结冰对飞行安全的影响、防/除冰系的设计以及飞机的结冰适航取证等研究之中,复杂冰形的修正和简化方法的首要问题就是建立一套科学的结冰外形相似度评估和判定的方法[7-8]。
另外,数值仿真方法得到的冰形与实验数据以及其他软件仿真结果的对比、冰形试验的可重复性、冰形沿着展向变化规律等问题的研究也都需要对不同冰形进行相似度对比[9-10],这些研究工作的深入开展也依赖于科学的冰形相似度评估方法。
现阶段通常采取一些定性的方法进行比较,还没有一套被普遍认可的冰形相似度判定的量化标准,美国格林研究中心率先开展了一些研究,采用百分比差异方法对冰形基本的几何特征量进行简单比较[11],这项工作目前还处于初步探索的阶段,所提出的方法仅仅能够体现冰形在宏观的差异,几个特征量本身还存在一些相互矛盾之处,采用平均百分比差异的方法也没有考虑不同特征量之间的权重等问题,
国内在飞机结冰领域的研究起步较晚,用于生产试验的大型结冰风洞才刚刚建成,虽然在武汉,绵阳、沈阳等地有几座小型结冰风洞,但配套的测试设备、试验技术和理论尚需完善,从能公开查阅到的资料显示,目前对结冰风洞试验数据修正理论和方法以及与之紧密相关的冰形相似度判定准则及评估方法的研究国内尚属空白。
本文在Ruff[11]等的研究基础上进行了进一步的探索,提出了一种基于几何特征量、冰形差异率的冰形相似度的量化评估方法,并采用CFD手段分析不同相似度的冰块对NACA0012翼型气动性能的影响, 并对该方法进行了验证。
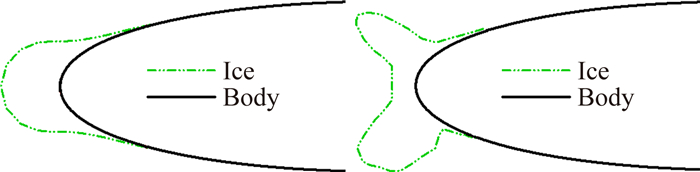
1 飞机冰形相似问题由于空气含水量和过冷水滴温度的不同、冻结过程中释放潜热排走的快慢不同,冻结过程形成的冰层在结构、强度、外观上有较大差异,外形轮廓大体上可以分为流线型和角状型两大类型,如图 1所示[12]。
|
| 图 1 典型冰形 Fig. 1 Typical ice shape |
结冰对气动特性、飞行特性的影响取决于结冰外形对流场的扰动作用[13]。因此,冰风洞试验或数值仿真方法模拟结冰过程时,最重要的一项内容就是得到飞机结冰的外形轮廓。而不同的冰风洞之间、计算结果与试验结果之间、不同软件的计算结果之间等进行对比验证时,以及同一冰风洞进行重复性试验时,最终的检验都需要评估不同的冰形是否具有相似性以及其相似程度[14]。
现阶段,结冰相似性研究依赖于视觉上的定性研究。以机翼结冰为例,通过跟踪单个的冰的外形轮廓得到冰形曲线,然后采用定性的方式对不同冰形曲线进行对比。在科学研究和工程实际过程中需要对试验或数值模拟结果的准确度进行量化的判定,而现阶段的方法往往只能得到“基本相似”等定性化的结论,这就需要建立一套科学的结冰外形相似度的量化评估方法[15]。
2 冰形相似度评估方法与普通的图形识别方法不同,冰形之间的差异往往较大,用于微观方面差异识别的基于矢量、三角剖分等算法的匹配方法并不适用于冰形相似度的量化评估。冰形相似的量化评估方法必须建立在试验或仿真过程目的特性的基础上,采用冰风洞试验或数值仿真方法得到冰形,目的是为了进一步得到结冰对气动特性、飞行特性的影响,因此,如果两种冰对飞行器气动特性、飞行特性的影响相似,就可以认为这两种冰形是相似的。冰对气动特性、飞行特性的影响度取决于冰形对周围流场的扰动作用的大小,通常,扰动源的宏观轮廓是影响度的主要决定因素,另外,由于冰是一个复杂的外形,仅仅依靠宏观轮廓还不能完全描述冰对流场的扰动作用,冰形细节之间的差异同样会影响其对流场的扰动作用。因此,冰形的相似度判定应该从宏观轮廓和冰形细节之间来提炼出一个综合相似度因子。结冰外形的综合相似度因子由两个量决定,一个为体现冰形典型几何特征相似性的特征量相似率,另外一个为体现冰外形细节相似性的冰形差异率,下面分别对这两个参数进行介绍。
2.1 冰形几何特征量冰的宏观轮廓可以通过提炼冰形几何特征量的方法来描述,针对流线型和角状型两种不同的冰,分别提炼出不同的几何特征量。
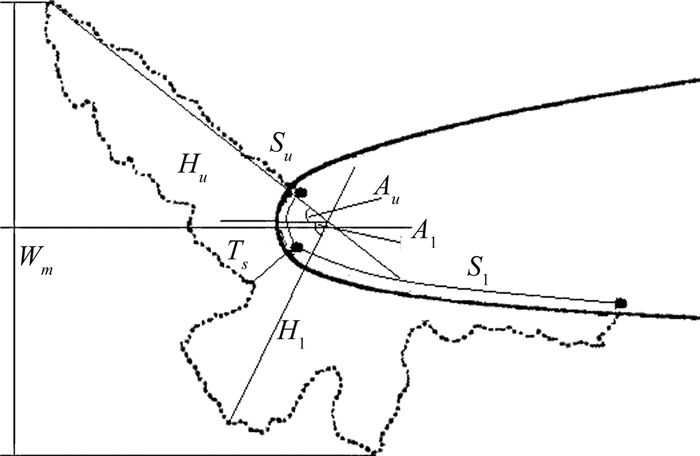
冰形特征量的建立,主要是为了从冰的宏观轮廓方面来衡量结冰外形对气动特性的影响,从外形可看出,角状冰最关键的参数是两个冰角以及冰角的长度,以及驻点处结冰厚度。冰形特征量可以由以下8个特征量来描述:驻点厚度Ts,冰宽度最大宽度Wm,冰角特征包括上、下冰角的长度(Hu和Hl)以及上下冰角的角度(Au和Al),结冰极限特征包括上极限Su和下极限Sl。如图 2所示。
|
| 图 2 各特征量计算方法 Fig. 2 Calculation method of geometric measurements |
而Ruff提出的角状冰特征量方法中,另外包含冰的最大厚度和极限厚度两个量,冰的最大厚度特征可以从冰角及其长度来体现,冰的极限厚度对流场的扰动影响相对较小,其特征可以从上下两个极限的值来体现,这两个量对流场的影响相对较小,它们的加入会降低主要特征量的权重,对冰型的特征量描述中将其忽略。冰的最大宽度特征也可从冰角长度及角度中体现,但是由于冰角长度及角度对流场的影响起着决定性的影响,另外,最大宽度本身也能体现冰形的具体特征,这个量与冰角角度与长度参数同时添加进来,以增加这方面特征量的权重。
流线型冰相对比较简单,采用驻点厚度Ts,冰宽度特征包括最大宽度Wm和极限宽度Wi,结冰极限特征包括上极限Su和下极限Sl等五个特征量就能基本描述其宏观轮廓,本文重点针对角状冰的特征进行分析。
根据冰的外形的描述以及冰形的特征量的提取,发展了一种特征量计算模型,如图 2所示,具体如下:
第一步,针对典型冰形,以翼型前缘处为分界线,将二维冰形分为上下两部分;
第二步,沿上下表面分别搜索冰形离物面最远的点,搜索过程中对冰形每一个单元段进行内插值,分别计算各点离物面的距离。这两个点即为上下冰角点,其距离分别即为上、下冰角的长度(Hu和Hl),上下冰角的角度(Au和Al);
第三步,搜索两个冰角点之间离物面最近处的点,该点即为驻点,驻点厚度为Ts;
第四步,计算冰形上下极限点离驻点的长度,分别记为上极限Su和下极限Sl;
第五步,搜索冰形沿Y坐标的上下极限,其差值即为最大厚度Tm。
根据以上结冰外形几特征参数,引入百分比差异的概念用于对比两种结冰外形是否相似,其定义式为:
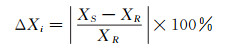
|
(1) |
其中,Xi为冰形几何特征,对于角状冰,i的取值范围为1~8,对于流线型冰,i的取值范围为1~5,下标R代表参考冰形,下标S代表对比冰形。
根据式(1)将得到5个(流线型冰)或者8个(角状冰)数据,不能直接给出冰形相似度的判定,为了得到唯一的判定依据,引入平均百分比差异判定法,定义
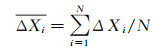
|
(2) |
式(2)中,N为5(流线型冰)或者8(角状冰)。很明显,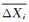
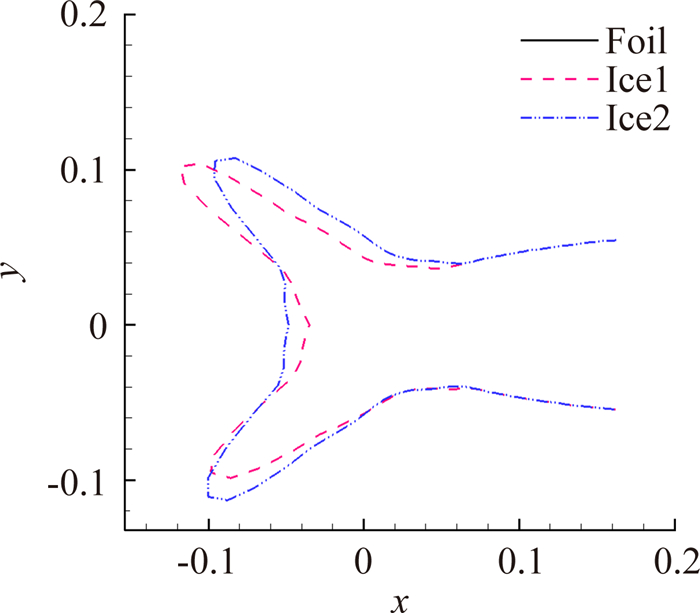
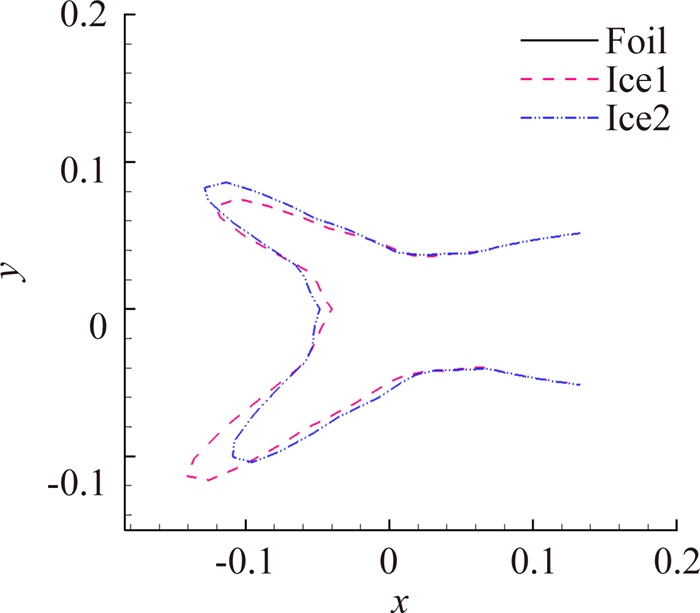
以NACA0012翼型上的冰形为例,采用平均百分比差异判定法进行了冰形相似度的比较,图 3和图 4分别为不同相似度的两组冰形,这两组冰形的相似度比较接近,很难通过目测直接得到哪一组相似度更好的结论,采用上述几何特征量方法,从表 1和表 2可以看到,图 3中的这组冰形几何特征量平均百分比差异为13.3,而图 4中这组冰形的几何特征量平均百分比差异为11.4。图 4中的冰形几何特征的相似度要稍高一点。
|
| 图 3 NACA0012翼型上两种冰形对比(1) Fig. 3 Ice shapes on NACA0012 airfoil (1) |
|
| 图 4 NACA0012翼型上两种冰形对比(2) Fig. 4 Ice shapes on NACA0012 airfoil (2) |
| ΔXTs | ΔXWm | ΔXSu | ΔXSl | ΔXHu | ΔXHl | ΔXAu | ΔXAl | 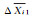 |
| 27.9 | 9.1 | 15.8 | 12.1 | 11.0 | 7.9 | 14.8 | 8.0 | 13.3 |
| ΔXTs | ΔXWm | ΔXSu | ΔXSl | ΔXHu | ΔXHl | ΔXAu | ΔXAl | 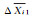 |
| 17.9 | 2.1 | 14.2 | 7.9 | 8.8 | 23.1 | 7.8 | 9.0 | 11.4 |
2.2 冰形差异率
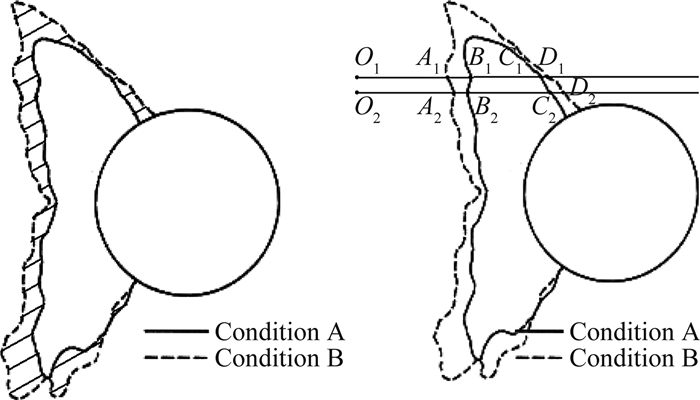
相似度达到100%的两个冰块对周围流动的扰动应该完全相似,显然,特征量相似率显然不能满足此项条件,纯粹基于几何特征量的相似率只能从冰形的宏观几何特征上来表征冰形之间的相似度,而冰形细节之间的差异同样对周围流动有着扰动作用,冰形细节之间的差异必须通过不同冰形之间的形位误差来体现,引入冰形差异率的概念来描述不同冰形之间的形位误差,定义为两个冰形所有不重叠面积之和与其两个冰形平均面积之比。如图 5所示,A冰形与B冰形的冰形差异率为阴影部分面积与A、B曲线所包含的平均面积之比。
|
| 图 5 冰形差异率 Fig. 5 Degree of difference between ice shapes |
由冰形差异率概念可知,得到求解形位误差的关键在于得到冰形的面积,可以采用数值积分求解封闭曲线面积的方法。其步骤如下:
第一步,通过一种射线法来判断线段、点与封闭曲线的关系,从封闭曲线外一个点向某个方向延伸出一条射线,从起点开始计算,当射线与封闭曲线有交点,且该交点的顺序数为奇数时,射线开始进入到封闭曲线内,当射线与封闭曲线有交点,且该交点的顺序数为偶数时,射线开始离开封闭曲线。
第二步,从远处O1、O2点沿x轴正方向作射线,由射线法可知,图中A1B1B2A2A1和C1D1D2C2C1两个区域属于两个冰形的不重叠部分,B1C1C2B2B1区域属于A冰形,A1D1D2A2A1属于B冰形。沿着y方向覆盖两个冰形的范围,每间隔Δy向x轴正方向作射线,Δy取一个足够小的量,采用积分方法可分别得到A、B冰形以及他们不重叠部分的面积。
第三步,由定义Rat=Sdif/Save求得冰形差异率,其中Rat为冰形差异率,Sdif两个冰形的不重叠部分面积,Save两个冰形的平均面积。
2.3 冰形相似度特征量相似率、冰形差异率这两个概念的提出是为了表征两个冰形之间的相似度,其中特征量相似率主要描述冰形之间的宏观几何特征的相似度,冰形差异率主要表征的是两个冰形细节之间的差异率。判断冰形相似度需要综合考虑这两个量,而在冰形处理如简化冰形等过程中,通常需要的是一个唯一的判定依据,通过加权计算的方法,可以得到一个冰形相似度的计算公式:
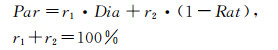
|
其中,Par为冰形相似度,Dia为冰形特征量相似率,r1、r2为加权因子,本文取:r1=0.7,r2=0.3。
3 结冰外形相似度评估方法的验证本文进一步采用CFD手段计算飞行器带相似度不同的冰块对飞行器气动性能的影响,以验证所提出结冰外形相似度评估方法的准确性。为便于量化对比分析,引入升力、阻力的相对影响度Beta的概念,升力、阻力的相对影响度分别定义为两个冰块对飞行器升力、阻力的影响量的差异与其平均影响量之比,相对影响度越小冰形越相似。
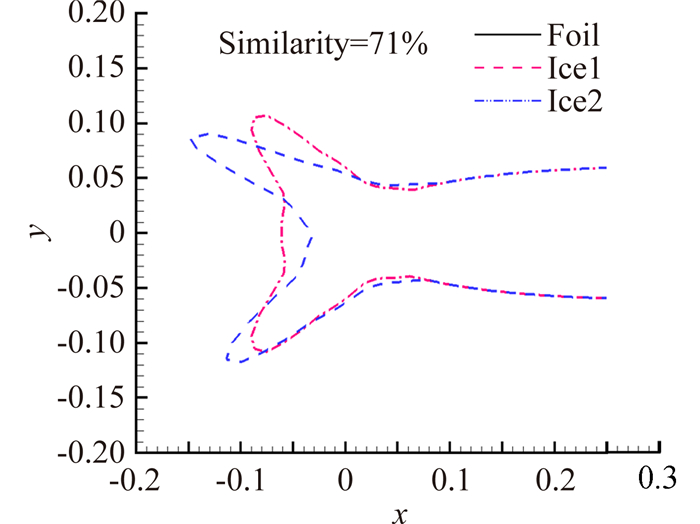
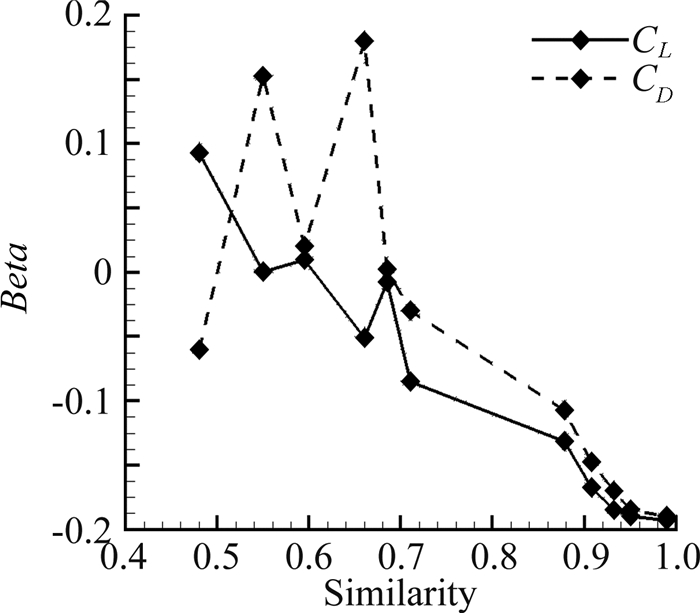
构造了不同相似度的冰形组,采用CFD手段分析带不同冰块的NACA0012翼型在一定气象条件下的气动特性,以研究冰形相似度与其对气动特性的影响关系。图 6、图 7、图 8分别为不同相似度条件下的典型冰形组合,给出的这三组冰形的相似度分别对应为54%、71%、93%。图 9是升力、阻力的相对影响度Beta与冰形相似度的关系,当冰形相似度较低时,冰形对气动性能的影响规律是无序的,由于此时冰形差异较大,目测就能得到冰形不相似的结论,进行定量分析的价值不是很高,当相似度大于85%时,相似度越高的冰块,升力和阻力的相对影响度都越小,对飞行器的气动性能影响也就越相似,这个结果验证了本文所提出冰形相似度评估方法的正确性。

|
| 图 6 相似度为54%的两种冰形 Fig. 6 Two ice shapes with similarity of 54% |
|
| 图 7 相似度为71%的两种冰形 Fig. 7 Two ice shapes with similarity of 71% |

|
| 图 8 相似度为93%的两种冰形 Fig. 8 Two ice shapes with similarity of 93% |
|
| 图 9 相对变化量与冰形相似度的关系 Fig. 9 Variety of lift and drag with different ice |
4 结论
本文提出了一种冰形相似度的量化评估方法,并采用CFD手段进行了验证,得到如下结论:
1) 根据所提出的冰形相似度的量化评估方法,相似度越大的冰对飞行器的气动性能影响也就越相似,证明了本文所提出冰形相似度量化评估方法的正确性;
2) 本文所提出的冰形相似度的量化评估方法适用于相似度较高冰形之间的量化评估,相似度很低的冰形对气动性能的影响规律是无序的,其量化评估的价值本身不是很大,可以采用目测的方式直接定性评估;
3) 基于几何特征量、冰形差异率的冰形相似度量化评估方法,不仅能体现冰形宏观轮廓特征,也能体现冰形之间的微观差异,这一点与当前的相似度量化评估方法具有显著差异;
4) 相比于Ruff的特征量方法侧重于冰外形整体相似性,本文提出的几何特征量更侧重于冰对气动力的影响,所提炼的特征量有所差异。
本文所建立的特征量描述方法中,各特征量之间存在相关现象,如最大厚度与冰角特征之间存在相关性,完善的冰形特征量描述方法必须提炼出完全相互独立的基本特征量,并根据冰形对气动力的影响得到各基本特征量的权重,这也是本文工作下一步需要改进之处。
| [1] |
Yang Qian, Chang Shinan, Yuan Xiugan. Study on numerical method for determ ining the droplet trajectories[J].
Acta Aeronautica et Astronautica Sinica, 2002, 23(2).
(in Chinese) 杨倩, 常士楠, 袁修干. 水滴撞击特性的数值计算方法研究[J]. 航空学报, 2002, 23(2). |
| [2] |
Yi Xian, Wang Kaichun, Gui Yewei. Study on Eulerian method for icing collection efficiency computation and its application[J].
Acta Aerodynamica Sinica, 2010, 28(5):596–601.
(in Chinese) 易贤, 王开春, 桂业伟. 结冰面水滴收集率欧拉计算方法研究及应用[J]. 空气动力学学报, 2010, 28(5) : 596–601. |
| [3] | Bourgault Y, Habashi W G, Dompierre J, et al. A finite element method study of Eulerian droplets impingement models[J]. Internernational Journal for Numerical Methods in Fluids, 1999, 29(4):429–449. DOI:10.1002/(ISSN)1097-0363 |
| [4] | Bragg M B, Broeren A P, Addy H E, et al. Airfoil ice-accretion aerodynamics simulation. AIAA 2007-0085[R]. Reston:AIAA, 2007. |
| [5] | Bragg M B, Broeren AP, Blumenthal L A. Iced-airfoil aerodynamics[J]. Progress in Aerospace Sciences, 2005, 41(5):323–418. DOI:10.1016/j.paerosci.2005.07.001 |
| [6] | Lee S, Bragg M B. Effect of simulated-spanwise ice shapes on airfoils:experimental investigation. AIAA-99-0092[R]. Reston:AIAA, 1999. |
| [7] | Anderson D N. Further evaluation of traditional icing scaling methods, NASA TM 107140[R]. 34th Aerospace Sciences Meeting, Reno:1996. |
| [8] | Papadakis M, Yeong H W, Shimoi K, et al. Ice shedding experiments with simulated ice shapes. AIAA 2009-3972[R]. Reston:AIAA, 2009. |
| [9] | Bragg M B, Gregorek G M. Aerodynamic characteristics of airfoils with ice accretions[R]. AIAA 20th Aerospace Sciences Meeting, 1992. |
| [10] | Ruff G A, Berkowitz B M. Users manual for the NASA Lewis ice accretion prediction code (LEWICE)[R]. NASA CR 185129, 1990. |
| [11] | Ruff G A. Quantitative comparison of ice accretion shapes on airfoils[J]. Journal of Aircraft, 2002, 39(3):418–426. DOI:10.2514/2.2967 |
| [12] | Lee S, Barnhart B P, Ratvasky T P, et al. Dynamic wind-tunnel testing of a sub-scale iced business jet. AIAA 2006-0261[R]. Reston:AIAA, 2006. |
| [13] | Papadakis M, Gile Laflin B E, Youssef G M, et al. Aerodynamic scaling experiments with simulated ice accretions. AIAA 2001-0833[R]. Reston:AIAA, 2001. |
| [14] | Papadakis M, Rachman A, Wong S C, et al. Water impingement experiments on a NACA 23012 airfoil with simulated glaze ice shapes. AIAA 2004-0565[R]. Reston:AIAA, 2004. |
| [15] | Lee S, Bragg M B. Experimental investigation of simulated large-droplet ice shapes on airfoil aerodynamics[J]. Journal of Aircraft, 1999, 36(5):844–850. DOI:10.2514/2.2518 |



