在遇到结冰气象条件时,飞机及发动机等部件的气动性能会由于结冰而恶化,严重影响飞机飞行安全。特别是过冷大水滴结冰时,会出现水滴撞击区域变大、更容易形成复杂冰形等情况,对飞行安全的危害会更加严重。目前过冷大水滴结冰机理和结冰过程的研究,已成为飞机结冰问题研究的热点之一,并得到了广泛关注。
近些年来,人们对过冷大水滴结冰进行了深入研究[1-2]。过冷大水滴与常规小水滴的一个主要区别是会出现显著的动力学特性,例如变形破碎、撞击飞溅等,会造成水滴轨迹变化,导致结冰收集系数的变化,而对结冰量和结冰位置产生较大影响。过冷大水滴结冰冰形的产生是多个动力学特性和热力学过程的综合作用结果。
美国联邦航空管理局的规章制定通告,将航空管理条例FAR 25部和33部适航规章确定的结冰条件扩展到了过冷大水滴结冰条件,同时建议增加了新的适航标准以改善安全性[3-4]。欧美发达国家的结冰数值分析软件,例如LEWICE等,通过研究过冷大水滴撞击特性及其对结冰过程影响,改进其软件内容,研究工作还在深入完善[5-6]。对过冷大水滴结冰环境,Vargas等[7]通过实验研究分析了大水滴在不同风速下的变形和破碎特性,给出了运动过程中水滴各参数的变化,比如韦伯数、雷诺数和阻力系数等;Quero等[8]通过与实验结果的对比研究,分析了几种飞溅和反弹模型的计算精度和适用范围以及影响规律。国内对过冷大水滴结冰数值模拟的研究工作开展得比较晚,周志宏和易贤等[9]进行了过冷大水滴结冰过程中的动力学效应研究;张辰和刘洪等[10]对大水滴的破碎过程和破碎判定准则进行了模拟研究;胡剑平等[11]大水滴环境下发动机进口支板的水滴撞击特性进行了研究。还有其它一些科研院所和高校科研团队正在不断加入到过冷大水滴结冰问题研究中来[12-14]。
本文通过对过冷大水滴条件下结冰条件及机理进行分析,基于动力学特性,分析过冷大水滴结冰过程及其影响规律。使用基于泰勒类比理论的变形破碎模型,对水滴运动和成冰过程进行模拟,分析水滴变形破碎对水滴运动和冰型生成的影响;采用飞溅计算模型,研究水滴飞溅对成冰过程和结果的影响;最后分析了水滴多尺度分布对撞击特性及结冰过程的影响规律。通过研究分析,说明过冷大水滴条件时考虑水滴动力学效应的必要性和计算方法的可行性,获得的影响规律和结论对于深入研究结冰问题具有重要参考价值。
1 常规水滴结冰计算方法结冰过程的数值模拟是基于对结冰机理的认识和探索,预测结冰的范围和形状及其影响,主要包括以下四步:空气流场计算、水滴运动及撞击特性分析、结冰过程计算、冰形确定。
1.1 空气流场计算流场中过冷水滴的运动、水滴与物面的碰撞以及物面结冰的相变过程等都在很大程度上决定于空气流场分布。因此,获得空气流场的基本信息是用数值手段进行结冰研究的基础。
非定常N-S方程可写成如下积分形式:
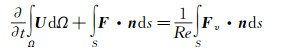
|
(1) |
其中F为对流项,Fv为粘性耗散项。
采用有限体积法和经典四步Runge-Kutta方法求解上述方程,利用Spalart-Allmaras一方程湍流模型,对于物面边界和远场边界,分别采用无穿透和无反射边界条件。算法详见文献[12]。
1.2 水滴运动及撞击特性分析在空气流场计算的基础上或与此同时,采用数值方法求解水滴运动方程得到水滴运动轨迹,获得结冰表面水滴撞击特性。本文基于拉格朗日方法来分析撞击特性并获得水滴收集系数[13-15]。
用拉格朗日法进行水滴流场求解时,对每个水滴进行跟踪,以确定水滴是否与物体发生碰撞,并确定碰撞位置。计算过程有如下假设:
1) 水滴在运动过程中既不碰撞也不分解;
2) 水滴的密度、温度等在运动中保持不变;
3) 水滴初速度与自由来流相同,水滴流场不会对空气流场产生影响。
考虑到作用在水滴上的阻力、重力和浮力,根据牛顿第二定律获得水滴的运动方程为:
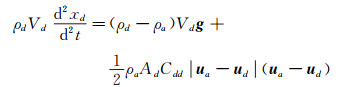
|
(2) |
其中,ρd为水滴密度,Vd为水滴体积,ρa为空气密度,u a为空气速度,u d为水滴速度。Cdd为水滴阻力系数,对于常规水滴采用如下公式[12]:
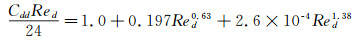
|
(3) |
通过求解式(2)分别跟踪每一个水滴,由水滴的初始位置,令此水滴的初始状态为该点空气流场的状态,然后计算Δt时刻后水滴的新位置。由此推进计算,直到水滴与翼面碰撞或者水滴运动到预先设定的计算区域以外,再对下一个水滴进行如此追踪,直到获得所有水滴的运动轨迹。在得到所有碰撞水滴的轨迹后,可以由水滴的初始位置和碰撞位置,得到局部收集系数。
1.3 结冰过程计算与冰形确定在空气流场及水滴撞击特性已知的基础上,对热力学系统建立传质传热模型,获得结冰表面的液态水分布及冻结量等,由给定时间内的冻结量得到每个控制体内冰层厚度的增长,从而在时间推进过程中完成结冰形状的变化计算和修正。
在结冰预测研究中,热力学过程的描述常采用基于平衡关系的Messinger模型。根据质量和能量守恒,控制体内的质量和能量平衡方程分别为:
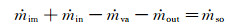
|
(4) |
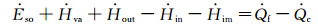
|
(5) |
在进行方程联立求解时,先确定结冰翼面驻点位置,与驻点相邻控制体内有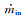
对于过冷大水滴,结冰过程模拟将出现一系列问题和变化,比如水滴的变形破碎、水滴飞溅所引起的质量及传热特性变化、水滴多尺度分布对结冰过程的影响等。
2.1 大水滴动力学特性及计算模型为了更好模拟大水滴变形后轨迹,需要对水滴阻力系数重新评估,本文采用如下模型[16]:
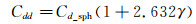
|
(6) |
其中γ表示水滴变形程度的大小,其表达式为:

|
(7) |
式中d0为水滴未发生变形时的初始直径,δ为水滴球赤道处半径的形变量。式(6)中Cd_sph表示球形颗粒阻力系数,为了计及雷诺数对该阻力系数大小的影响,对比式(3),采用如下不同形式:
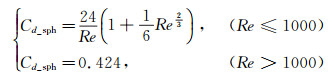
|
(8) |
对于破碎问题,Ibrahim等[17]提出了使用泰勒类比模型(TAB)模拟液滴破裂的详细理论,通过对控制液滴振荡与变形的TAB模型方程进行求解就可得到任意时刻液滴的振荡与变形。液滴受迫变形的控制方程为:
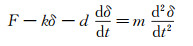
|
(9) |
上述方程的系数来源于泰勒类比:
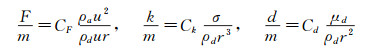
|
(10) |
其中,u为液滴相对速度,r为未发生变形前的液滴半径。依据实验数据经过理论推导[17],可知无量纲常数CF=1/3、Ck=8、Cd=5,由此可得液滴破碎时的临界Weber数约为13。
另一方面,Dai和Faeth使用脉冲全息照相技术对水滴破碎过程进行了拍摄,得到了水滴破碎后直径大小的预估公式[18]:
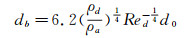
|
(11) |
其中d0与db分别表示破碎前后的液滴直径。一旦破碎后的子液滴尺寸求出之后,通过质量平衡就可以得到子液滴的数目,子水滴的位置和运动速度仍取当地值。使用本节中的方程求出破碎后的各子水滴参数,之后再用与不发生破碎时同样的方法获得水滴此时的阻力系数,传回水滴流场计算程序,采用拉格朗日方法获得局部水收集系数[12-13]。
在过冷大水滴结冰模拟中,水滴飞溅是一个不可忽略的过程。Mundo等[19]根据对水滴飞溅的实验研究,提出水滴撞击飞溅主要取决于水滴Re数和Oh数等无量纲参数。引入水滴撞击参数K,表示水滴撞击能的大小,其表达式为[19-20]:
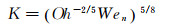
|
(12) |
其中Wen为水滴的撞击Weber数,与水滴法向入射速度相关。根据Mundo实验研究,撞击水滴如果满足K ≥57.7,将会发生飞溅现象。水滴飞溅的质量损失率可表示为[19-20]:
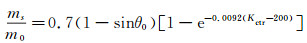
|
(13) |
式中, ms为水滴碰撞过程中损失的质量,m0为撞击液滴的总质量,θ0表示水滴入射速度与碰撞表面切向的夹角,Kctr表示水滴飞溅的临界值[20]。
为了进一步获得水滴飞溅后运动轨迹,判断水滴是否会与翼面发生二次碰撞,需要知道飞溅出的水滴大小和飞溅速度。设t代表切线方向,n代表法线方向,ξ和ζ分别表示水滴飞溅速度与入射速度在切向和法向分量的比值,并且设飞溅水滴直径为ds,撞击水滴直径为d0,则可得[20-21]:
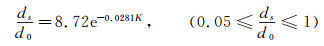
|
(14) |
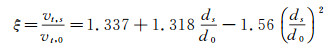
|
(15) |
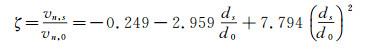
|
(16) |
在Mundo模型中,认为水滴的飞溅后的运动状态主要受到了飞溅水滴大小的影响。
2.2 大水滴多尺度分布特性在实际飞行时云层中水滴直径不是单一的,而是按照一定规律分布的。在一般结冰研究中用水滴平均容积直径(MVD)作为水滴直径参考值。不同尺寸水滴在总液态水中所占比例分布称为水滴尺寸分布函数FLWC[22],实际飞行时FLWC受到当地温度、海拔和气候条件等各种因素的影响。
由于水滴尺寸会对水滴局部收集系数和结冰过程产生影响,为了改善过冷大水滴结冰数值模拟的精度,应该考虑水滴多尺度分布特性。
在数值计算过程中,水滴尺寸按照一定的比例以离散的形式输入,分析多尺度分布水滴撞击特性的方法是将多尺度分成多个单一尺度单独计算,在得到每个物面段上针对所有尺寸水滴的局部收集系数后,多尺度分布水滴的局部收集系数可以由以下计算式求得:
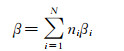
|
(17) |
其中, ni为第i类水滴的质量比例,βi为第i类水滴的局部收集系数。
不同飞行条件下水滴尺寸分布是不同的,所以每种条件下的最佳多尺度分布计算条件也会有所差别。在实际应用中,一般选用能够较好反映冰风洞喷雾模拟的Langmuir D粒子尺寸分布[22],此时水滴尺寸和质量比例如表 1所示。
| di/MVD | 0.31 | 0.52 | 0.71 | 1.00 | 1.37 | 1.74 | 2.22 |
| 质量比例 | 0.05 | 0.10 | 0.20 | 0.30 | 0.20 | 0.10 | 0.05 |
3 算例及结果分析 3.1 常规水滴结冰过程模拟及验证分析
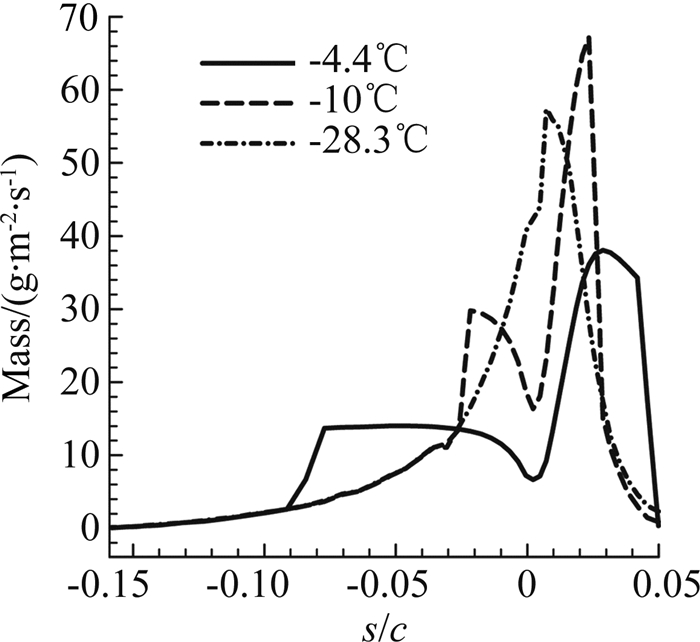
以广泛采用的典型NACA0012翼型为例,取翼型弦长c=0.5334m,来流速度u=67.05m/s,迎角α=4°,水滴平均容积直径MVD=20 μm,液态水含量LWC=1.0g/m3,结冰时间t=360s,选取三种不同结冰温度:Case1为T=-28.3℃(霜冰状态),Case2为T=-10.0℃(对应混合冰状态),Case3为T=-4.4℃(明冰状态)。
图 1显示了全部三种结冰温度下结冰质量分布的比较。随着结冰温度的不断升高,明冰范围逐渐变大,由图也可以看出在明冰和混合冰条件下翼型表面会出现两个分离的冰角。
|
| 图 1 结冰质量分布 Fig. 1 Icing mass on the surface |
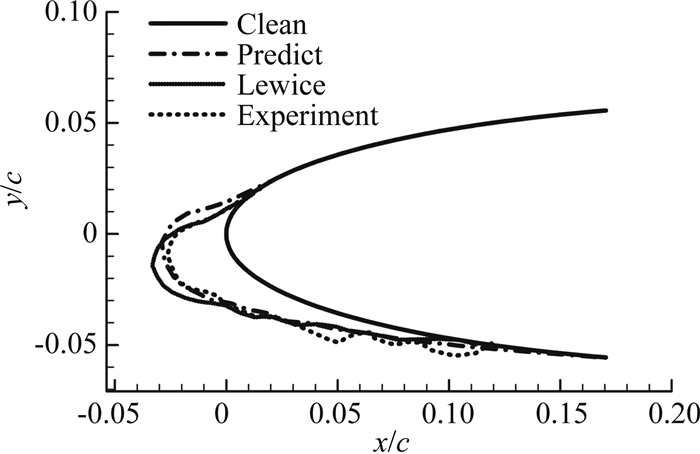
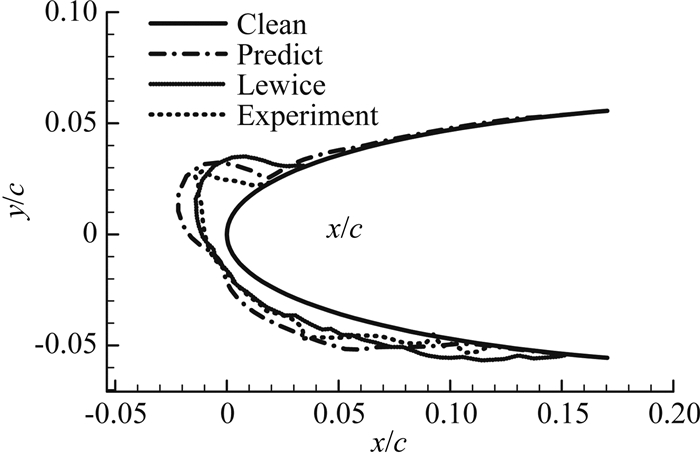
图 2和图 3分别为Case1、Case3条件下结冰计算结果及对比,用本文方法预测的冰形与实验结果以及LEWICE软件预测结果吻合良好,结冰上下极限位置一致,较准确的模拟出明冰中羊角产生的位置和方向,说明本文方法能够较好的预测常规小水滴结冰条件下的冰形生成过程。
|
| 图 2 Case1条件下结冰计算结果对比 Fig. 2 Comparison of computed results for Case1 |
|
| 图 3 Case3条件下结冰计算结果对比 Fig. 3 Comparison of computed results for Case3 |
3.2 大水滴动力学特性对结冰过程影响分析
同样以NACA0012翼型为例,取计算条件:翼型弦长c=0.5334m,来流速度u=90m/s,迎角α=0°,水滴平均容积直径MVD=490 μm,液态水含量LWC=1.0g/m3,结冰时间t=360s,结冰温度T=244.85K。
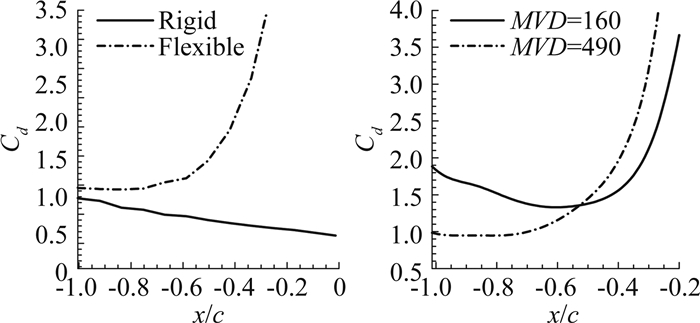
图 4给出了单个水滴阻力系数变化曲线。图 4(a)表示一个撞击翼型前缘点的水滴在加入和不加入变形模型两种情况下的阻力系数变化曲线,可以看出加入变形模型的水滴相比于没有变形的球形水滴的在靠近翼型前缘的过程中,阻力系数会有一个较大的上升。这是因为水滴由于变形引起其迎风面积变大,从而受到更大的空气阻力作用。图 4(b)表示不同大小水滴(MVD分别为160 μm和490 μm)在靠近翼型前缘点过程中的阻力系数变化。
|
| 图 4 水滴阻力系数变化曲线 Fig. 4 Computed drag coefficient of droplets |
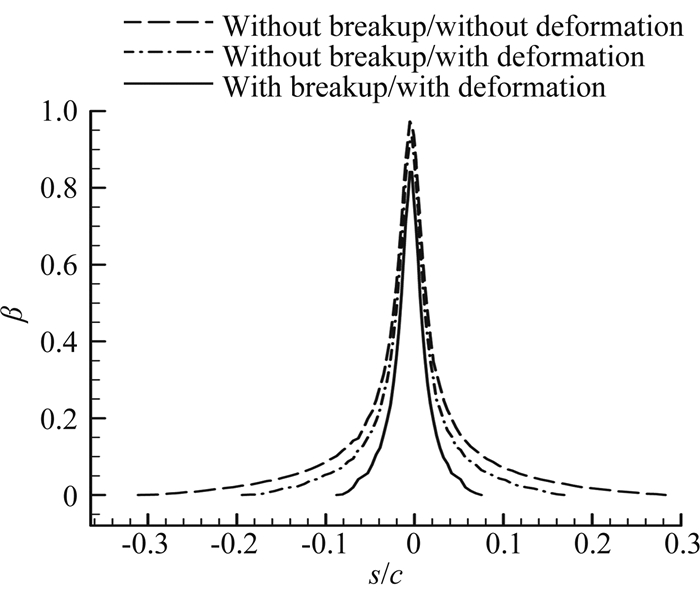
图 5给出了MVD=490 μm时撞击翼型前缘的水滴在不加模型,只加入变形模型和同时加入变形和破碎模型三种状态下的水滴收集系数曲线。在加入变形和破碎模型后,水滴的最大收集系数变小,撞击范围也有相应的减小。这是因为水滴由于变形破碎更容易受到空气流动影响,在撞击极限位置的水滴因此绕过翼型而向下游飞去。
|
| 图 5 不同状态的水滴收集系数 Fig. 5 Collection efficiency at different conditions |
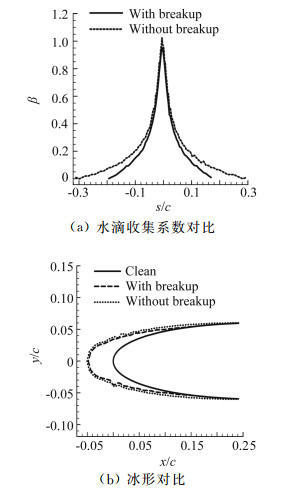
下面分析冰形生成,仍取本节NACA0012翼型计算条件,选取MVD=300 μm。由图 6可知,加入变形破碎模型后,上下撞击极限各减小了约1.1,最大收集系数减小了约0.4。说明对于大水滴,变形破碎的影响主要是改变了水滴的撞击范围,变形破碎对撞击前缘驻点附近区域的水滴,即最大收集系数附近的水滴轨迹影响相对较小,水滴的最大收集系数的位置和大小几乎没有明显的变化。
|
| 图 6 结冰计算结果对比图 Fig. 6 Comparison of computed results |
水滴飞溅影响主要表现在大尺寸水滴在撞击到翼面后由于撞击能量较大,不会立刻附着到翼面而是发生飞溅,部分水滴会离开表面。
以NACA0012翼型为例,取计算条件:翼型弦长c=0.5334m,来流速度u=77m/s,α=0°,MVD=160 μm,液态水含量LWC=1.0g/m3,结冰时间t=360s,结冰温度T=244.85K。本文采用Mundo飞溅模型,来分析水滴飞溅效应及其对结冰过程和冰形生成的影响。
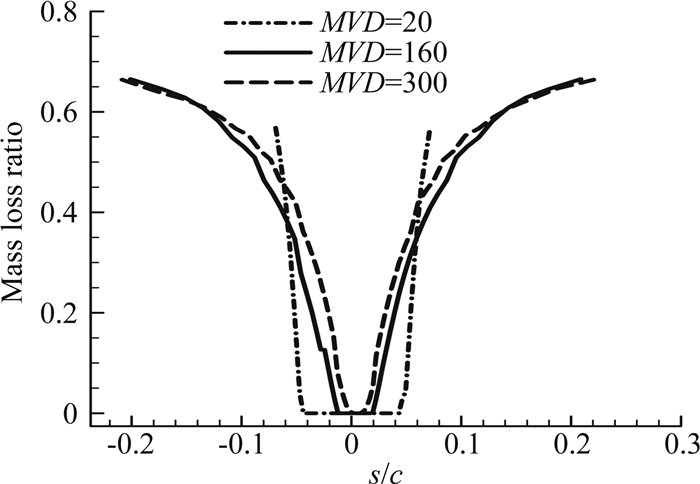
图 7为三种不同大小的水滴的飞溅质量损失率比较图。对于小尺寸水滴,只在两边撞击极限位置有很少的飞溅产生。而大尺寸水滴时,大部分碰撞位置均有飞溅情况发生,只在最大收集系数位置有少量区域由于撞击角度较大而不发生飞溅。而且越靠近两边碰撞极限,水滴飞溅导致的质量损失也就越大。同时水滴尺寸的增大也会引起飞溅范围变大,相同位置的飞溅质量损失率也越大。
|
| 图 7 不同水滴飞溅质量损失率对比 Fig. 7 Comparison of splashing mass loss for droplets |
图 8给出MVD=300 μm时加入飞溅模型和不加模型时的水滴收集系数和生成冰形的对比。可以看出,加入飞溅模型后,最大水滴收集系数的大小和位置、水滴撞击极限的位置都不会出现太大的变化,但整个水滴撞击区域内的收集系数会有明显的减小。这种变化反映到冰形上可以看出,结冰的极限位置和最大结冰厚度几乎没有改变,但是总结冰量却因为飞溅而变小,导致冰形发生变化。
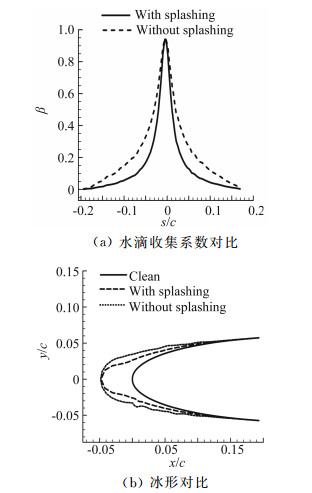
|
| 图 8 有无飞溅模型时计算结果对比 Fig. 8 Comparisons of computed results at splashing |
3.3 大水滴多尺度分布的影响分析
本节使用模拟大水滴多尺度分布时最常用的典型Langmuir D粒子尺寸分布,来探讨多尺度分布对过冷大水滴结冰过程的影响。
以NACA0012翼型为例,取计算条件:翼型弦长c=0.5334m,来流速度u=52m/s,迎角α=0°,液态水含量LWC=1.5g/m3,温度T=244.85K。设Case1为MVD=20 μm,Case2为MVD=80 μm,Case3为MVD=160 μm,讨论水滴多尺度分布对翼型表面水滴收集系数的影响。
图 9为Case2时水滴收集系数对比图,其中图 9(a)给出了Langmuir D分布条件下的每个单独组分水滴收集系数比较,图 9(b)是单尺度条件与多尺度条件下得到的水滴收集系数对比图。由图可知,在多尺度分布条件下,由于考虑到了更多不同直径水滴的影响,导致了水滴撞击范围的变大。
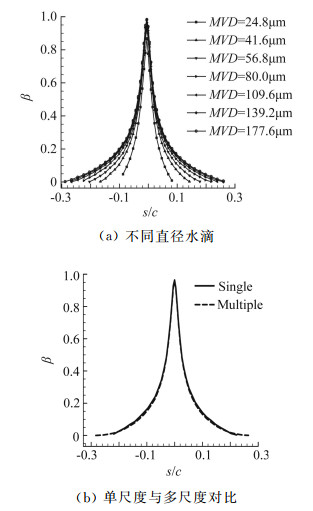
|
| 图 9 Case2条件下水滴收集系数对比 Fig. 9 Comparisons of collection efficiency for Case2 |
表 2给出了三种情况下水滴撞击极限位置的对比,其中su、sd分别代表上下翼面水滴撞击极限与驻点的距离。Case1时,加入多尺度模型后撞击范围增加了一倍,而随着MVD值变大,多尺度分布对水滴撞击范围的影响变小,Case3时加入多尺度模型后撞击范围只比单尺度情况下增加约8%,这是因为水滴尺寸越大导致其惯性也越大,受空气流动影响后运动轨迹越难以改变。
| 单一分布 | 多尺度分布 | 增长率 | ||
| Case1 | su sd |
0.079 0.068 |
0.161 0.148 |
103% 117% |
| Case2 | su sd |
0.219 0.223 |
0.261 0.265 |
19.1% 16.8% |
| Case3 | su sd |
0.283 0.265 |
0.306 0.287 |
8.1% 8.3% |
4 结论
本文主要开展了针对过冷大水滴条件下,在考虑其动力学特性和水滴多尺度分布时,翼型结冰过程及影响规律研究。结论如下:
1) 基于泰勒类比理论的变形破碎模型,对过冷大水滴的变形和破碎过程进行了模拟,探究了大水滴的变形破碎对水滴运动规律和成冰过程的影响。结果显示对于过冷大水滴结冰条件,变形破碎的影响主要是改变了水滴运动轨迹和撞击范围,使水滴的撞击极限变小。
2) 针对过冷大水滴结冰过程,讨论了Mundo水滴飞溅模型,分析研究了过冷大水滴条件下水滴飞溅过程运动规律及其对成冰结果的影响。结果显示水滴飞溅过程对结冰的极限位置和最大结冰厚度影响不大,但却使水滴的总收集系数变小,使得翼型前缘的冰形更容易出现变化。
3) 采用了Langmuir D分布,研究了水滴多尺度分布条件对水滴收集系数和撞击极限位置的影响规律,通过对过冷大水滴结冰过程的分析,说明了充分考虑大水滴动力学效应,可以更好地模拟水滴运动轨迹和撞击特性。
| [1] | Lee S, Bragg M B. Experimental investigation of simulated large-droplet ice shapes on airfoil aerodynamics[J]. Journal of Aircraft, 1999, 36(5):844–850. DOI:10.2514/2.2518 |
| [2] | Dunn T A, Loth E, Bragg M B. Computational investigation of simulated large-droplet ice shapes on airfoil aerodynamics[J]. Journal of Aircraft, 1999, 36(5):836–843. DOI:10.2514/2.2517 |
| [3] | FAA. Transport certification update:improving operation in icing conditions[EB/OL]. 2010, http://www.faa.gov/aircraftair-cert/design-approvals. |
| [4] | FAA. Aircraft ice protection appendix K:ice and icing condition detection[S]. AC20-73A, 2006. |
| [5] | Reid T, Baruzzi G, Ozcer I, et al. FENSAP-ICE simulation of icing on wind turbine blades Part 1:performance degradation. AIAA 2013-0750[R]. Reston:AIAA, 2013. |
| [6] | Colin S, Bidwell C S. Super cooled large droplet analysis of several geometries using LEWICE3D Version 3. AIAA 2010-7675[R]. Reston:AIAA, 2010. |
| [7] | Vargas M, Feo A. Deformation and breakup of water droplets near an airfoil leading edge[J]. Journal of Aircraft, 2011, 48(5):1749–1765. DOI:10.2514/1.C031363 |
| [8] | Quero M, Hammond D W, Purvis R, et al. Analysis of super-cooled water droplet impact on a thin water layer and ice growth. AIAA 2006-466[R]. Reston:AIAA, 2006. |
| [9] |
Zhou Z H, Yi X, Gui Y W, et al. Study of dynamics effects in the SLD icing process[R]. Chinese Congress of Theoretical and Applied Mechanics, August, 2015, Xi'an, China. (in Chinese) 周志宏, 易贤, 桂业伟, 等. SLD结冰过程中的动力学效应研究[R].中国力学大会, 2013年8月, 中国西安. |
| [10] |
Zhang C, Kong W L, Liu H. An investigation on the breakup model for icing simulation of supercooled large droplet[J].
Acta Aerodynamica Sinica, 2013, 31(2):144–150.
(in Chinese) 张辰, 孔维梁, 刘洪. 大粒径过冷水滴结冰模拟破碎模型研究[J]. 空气动力学学报, 2013, 31(2) : 144–150. |
| [11] |
Hu J P, Liu Z X, Zhang L F. Supercooled large droplet impact behaviors on an aero-engine strut[J].
Acta Aeronoutica et Astronautica Sinica, 2011, 32(10):1778–1785.
(in Chinese) 胡剑平, 刘振侠, 张丽芬. 发动机整流支板大尺寸过冷水滴撞击特性[J]. 航空学报, 2011, 32(10) : 1778–1785. |
| [12] |
Lu T. Numerical simulation of ice accretion at multi-scale distribution of large droplets over airfoil[D]. Xi'an:Northwestern Polytechnical University, 2014. (in Chinese) 鲁天.大水滴多尺度分布翼型结冰过程数值分析[D].西安:西北工业大学, 2014. |
| [13] |
Zhou Z H, Yi X, Gui Y W, et al. An efficient method to simulate water droplet trajectory and impingement[J].
Acta Aerodynamica Sinica, 2014, 32(5):712–716.
(in Chinese) 周志宏, 易贤, 桂业伟, 等. 水滴撞击特性的高效计算方法[J]. 空气动力学学报, 2014, 32(5) : 712–716. |
| [14] | Bai J Q, Li X, Hua J, et al. Ice accretion simulation in supercooled large droplets regime[J]. Acta Aerodynamica Sinica, 2013, 31(6):801–811. |
| [15] | Villedieu1 P, Trontin P, Guffond D, et al. SLD Lagrangian modeling and capability assessment in the frame of ONERA 3D icing suite. AIAA 2012-3132[R]. Reston:AIAA, 2012. |
| [16] | Liu A B, Reitz R D. Modeling the effects of drop drag and breakup on fuel sprays[C]. SAE Paper 930072, 1993. |
| [17] | Ibrahim E A, Yang H Q, Przekwas A J. Modeling of spray droplets deformation and breakup[J]. Journal of Propulsion and Power, 1993, 9(4):651–654. DOI:10.2514/3.23672 |
| [18] | Dai Z, Faeth G M. Temporal properties of secondary drop breakup in the multimode breakup regime[J]. International Journal of Multiphase Flow, 2001, 27(2):217–236. DOI:10.1016/S0301-9322(00)00015-X |
| [19] | Mundo C, Sommerfeld M, Tropea C. On the modeling of liquid sprays impinging on surfaces[J]. Atomization and Sprays, 1998, 8(6):625–652. DOI:10.1615/AtomizSpr.v8.i6 |
| [20] | Wright W B, Potapczuk M G, Levinson L H. Comparison of LEWICE and glenn ICE in the SLD regime. AIAA 2008-439[R]. Reston:AIAA, 2008. |
| [21] | Trujillo M F, Mathews W S, Lee C F, et al. Modeling and experiment of impingement and atomization of a liquid spray on a wall[J]. International Journal of Engine Research, 2000, 1(1):87–105. DOI:10.1243/1468087001545281 |
| [22] | Shah A D, Patnoe M W, Berg E L. Droplet size distribution and ice shapes. AIAA-98-0487[R]. Reston:AIAA, 1998. |


