2. 国网新源张家口风光储示范电站有限公司, 河北 张家口 075000
2. Zhangjiakou Wind and Solar Power Energy Demonstration Station CO. LTD State Grid Xin Yuan Company, Zhangjiakou 075000, China
由于全球气候变暖和能源危机,传统能源模式已难以为继,加快新能源开发利用势在必行。海上风电容量大、效率高,已成为全球风电发展的最前沿方向。与此同时,恶劣的海洋环境制约着海上风力机的发展,强烈的日光照射、高浓度的盐雾环境、高湿度、水分侵蚀等因素都会对叶片表面造成损害,影响机组安全,增加运行维护成本[1-3]。
海洋环境湿度较大,我国渤海湾长年湿度在50%-95%之间,翼型及叶片周围压力、温度的变化在一定条件下会引起水蒸汽发生凝结现象。凝结不仅会显著改变翼型表面附近的压力、温度等流动参数,甚至还会引起稳定或振荡的激波,导致翼型升力、阻力特性发生改变,影响其气动性能[4-5]。此外,叶片表面结冰问题也与湿空气及凝结现象紧密相关,湿空气凝结是形成冰晶的重要机制之一[6]。
国内外许多研究机构和学者对湿空气凝结流动问题开展研究。NASA实验研究了湿空气凝结对机翼气动性能的影响[7]。Schnerr研究了均匀凝结流动中湍流边界层和冲击波相互作用[8];Rusak等[9]学者理论分析了凝结起始马赫数和凝结放热量等方面与凝结流动之间的相似性;Karabelas和Markato[10]数值研究了高对流条件下翼型的水蒸气凝结造成的影响;孙秀玲、李亮等[11-12]数值模拟了跨声速条件下RAE 2822翼型及ONERA M6机翼湿空气非平衡凝结流动对气动性能的影响。
研究表明:流动与凝结过程相互耦合,速度、迎角、空气湿度等参数与凝结过程相互影响,湿空气凝结对翼型升力、阻力特性有显著影响。尽管如此,在湿空气凝结流动研究方面,仍有一些重要的问题没有解决,温度、压力、相对湿度、速度及几何条件等对凝结发生及气动性能的影响,目前尚没有一般性的结论,凝结影响机翼气动性能的一般规律也并不清楚;且之前的研究多是针对航空翼型或机翼,针对风力机领域的研究还没有,特别是随着海上风电的大力发展,高恶劣海上气候条件对风力机叶片设计的要求更加苛刻,需要进一步了解湿空气对海上风力机叶片气动性能、噪声的产生传播乃至结构的影响。
本文以海上风力机高湿度环境为背景,考虑湿空气的物理特性及凝结过程,根据湿度不同,将湿空气考虑为水蒸气和空气的混合气体,采用输运模型研究翼型的升阻力,并与实验对比;在输运模型基础上,考虑凝结发生,通过FLUENT编写表面凝结自定义函数(UDF)实现翼型表面凝结,研究凝结发生情况下的翼型气动性能。
1 模 型常规翼型及风力机CFD计算,以干空气为流动介质。考虑实际海上湿度环境,将湿空气(干空气和水蒸气的混合气体)作为流动介质,采用组分输运模型,更接近实际情况,计算结果较干空气更加可靠。在输运模型基础上,考虑湿空气中水蒸气的凝结,通过编写用户自定义凝结函数,实现水蒸气在壁面凝结。
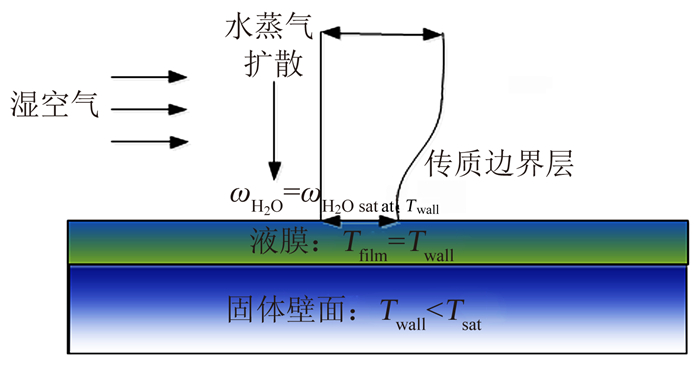
凝结原理(图 1):当湿空气流过物体表面,壁面温度低于该流体的饱和温度时,表面发生冷凝,形成液膜,且在流体重力和剪切力作用下流动。凝结过程中,非凝气体(空气)在气液交界面逐渐累积,阻碍蒸汽扩散到壁面,降低了水汽的凝结速率。尽管凝结是涉及流动、传质换热的多相耦合过程,但在某些条件下,凝结速率主要取决于蒸汽相的扩散过程。如果凝结液膜的热阻非常小,可以认为气液界面的温度与壁面温度相同,凝结速率可以通过求解蒸汽流动和非凝气体的分布预测。壁面冷凝边界条件允许蒸汽相质量传递,非凝气体为零净传质速率。
|
| 图 1 蒸汽壁面凝结原理 Fig. 1 Water vapor condensation on the wall |
基于以上原理,作以下假设:
①冷凝发生由于水蒸汽通过组分边界层扩散。
②液膜和壁面存在热平衡。
③气液界面是饱和状态。即交界面水蒸气分压力等于壁面温度下的饱和蒸汽压力。
④不考虑液膜运动带来的影响。由于流体剪切力和重力,液膜可能运动,但是运动不影响空气流动和凝结。
⑤分析仅限于膜状凝结,不考虑滴状冷凝。
⑥液膜的热阻忽略不计。
空气和水蒸气各组分的质量流量方程为:
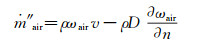 (1)
(1) 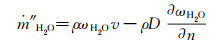 (2)
(2) 其中,ω为质量分数,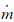
由二元混合物质量分数定义可得:
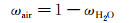 (3)
(3) 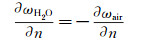 (4)
(4) 气液交界面混合物质量为:
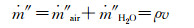 (5)
(5) 根据假设②由于液相只包含水,因此:
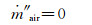 (6)
(6) 将公式(3)、(4)带入(1),联合公式(5)可得:
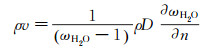 (7)
(7) 通过在近壁面使用质量(连续性)源项来代表冷凝率,即:
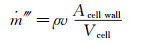 (8)
(8) 其中, 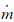
UDF中,假定壁面温度等于或小于表面水蒸气分压力对应的饱和温度时发生凝结。如果温度高于饱和温度,水蒸气质量分数等于壁面邻近单元的值。为了满足气液交界面局部热力学平衡的假设,当温度低于或等于饱和温度时,代表气液交界面的水蒸气质量分数被分配一个值,使得水蒸汽的分压等于水在局部壁面温度下的饱和压力。为此,近壁面邻近单元的组分方程中的源项必须包含扩散通量。
由公式(8)结合公式(2)、(5)、(6)得:
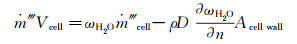 (9)
(9) 组分方程中移除壁面邻近单元的水汽量,等于连续方程中移除壁面邻近单元的水汽量,即:
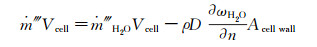 (10)
(10) 公式(10)减去公式(9)重排后得:
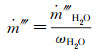 (11)
(11) 公式(11)中混合物的体积质量源项为:
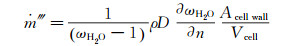 (12)
(12) 水蒸气的体积质量源项为:
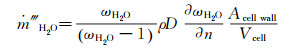 (13)
(13) 为验证翼型数值模拟方法的可行性,以NACA63418翼型为测试翼型,计算翼型的升力系数、阻力系数、表面压力系数等气动参数,并与实验数据对比,以验证本次计算的数值方法。为了便于与实验数据对比,网格划分方法及网格数参考文献[13],外流场计算边界取30倍弦长。测试翼型为标准翼型,弦长为1m,雷诺数Re=3 000 000,常温下空气密度ρ=1.225kg/m3,粘性系数μ=1.7894×10-5kg/m·s。
采用有限体积法求解偏微分方程,离散方程采用基于压力的simple算法求解,对流通量选取二阶迎风格式。为了解不同湍流模型对气动性能的影响,分别采用k-ω SST模型、S-A流模型、transition SST(4eqn)模型计算翼型的气动性能,并与实验数据对比。
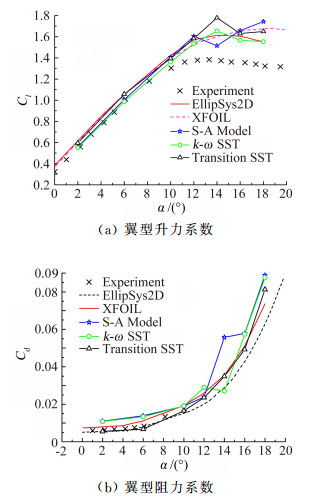
图 2为不同模型对应的升力系数和阻力系数。对比实验数据可以看出,三种模型整体上模拟结果与实验结果吻合较好,特别是在迎角小于10°时,各模型计算结果与实验值一致。升力系数方面,k-ω SST模型和S-A模型,其计算值与实验结果吻合度最高;而阻力系数Transition SST模型与实验结果最接近。迎角大于10°时,各模型计算结果与实验结果相差较大。综合考虑计算精度和计算时间,本次计算选取k-ω SST模型。
|
| 图 2 升力系数和阻力系数 Fig. 2 Lift coefficient and drag coefficient |
2.2 凝结模型验证
湿空气中水蒸气的凝结在许多工程应用中发挥重要的作用,例如空调设备、电厂换热器、湿烟气余热回收以及窗户结雾都涉及到水汽凝结。通过计算湿空气流过水平板后凝结与Sparrow[14]实验结果对比,来验证凝结UDF函数的可用性。图 3为计算几何模型。指定入口流体速度、温度、蒸汽质量分数及壁面温度,蒸汽质量分数根据相对湿度确定。通过表面凝结UDF计算气液交界面处凝结后的水蒸气质量分数。

|
| 图 3 平板几何及边界条件 Fig. 3 Geometry and boundary conditions for condensation onahorizontal flat plate |
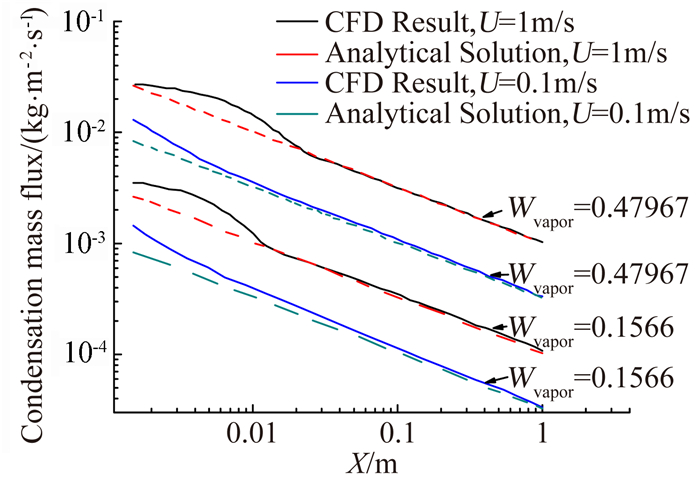
图 4是计算结果与强制对流凝结解析解[15]的对比。x轴为沿平板方向的距离,y轴为凝结速率(kg/m2·s)。CFD预测凝结速率除了平板前缘区之外,与解析解能够很好的吻合。结果表明,自定义函数能够满足凝结边界的求解。
|
| 图 4 CFD计算结果与解析解 Fig. 4 Analytical and CFD results for condensation rates |
3 结果分析
为全面地理解湿空气对翼型气动性能的影响,翼型的迎角计算2°、6°、10°、16°四种工况,翼型弦长为1m。考虑实际海上湿度范围一般为55%~95%,温度-20°~45°,本次计算选取相对湿度RH为25%、50%、70%、90%四种湿度工况,分别对应温度为30°和40°。湿空气根据温度和湿度考虑为干空气和水蒸气按相应比例的混合气体。
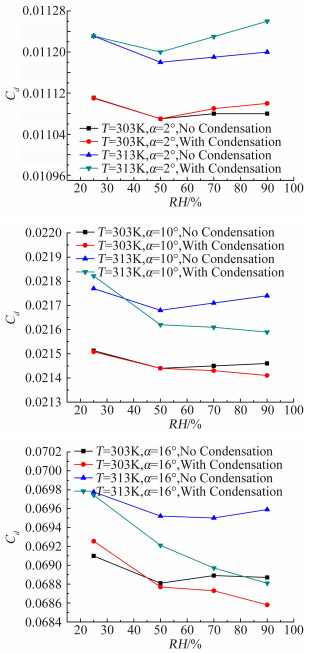
图 5为两种模型计算的对应三个迎角和两个温度下湿度对阻力系数的影响。由图看出,三种迎角阻力系数随湿度变化趋势不完全相同。2°迎角时,阻力系数先降低后增大。10°迎角和16°迎角时,除了温度为40°不考虑凝结的工况,其余工况阻力系数基本上随湿度增大而减小。阻力系数较升力系数,考虑凝结和不考虑凝结,两种模型变化趋势基本一致。同时可以看出,温度对阻力系数的影响,相同湿度条件时,温度高阻力系数高。
|
| 图 5 不同迎角阻力系数随湿度变化曲线 Fig. 5 Variation of the drag coefficient asa function of humidity level |
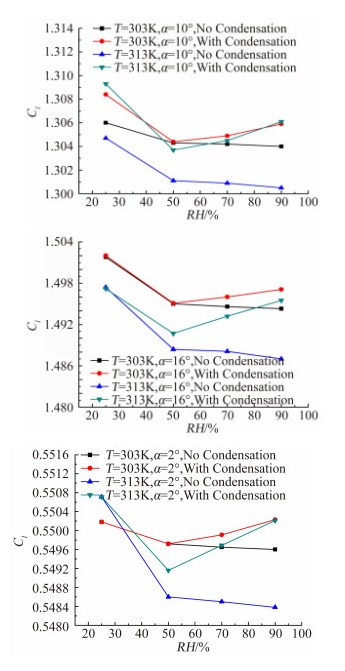
图 6为不同湿度下翼型升力系数曲线。可以看出,不考虑凝结时,组分输运模型计算升力系数变化趋势一致,随湿度增大升力系数减小。考虑凝结时,升力系数变化均先降低,再增大。主要是两种温度下,相对湿度为25%时,没有发生凝结,流动认为单相流动,气动性能改变主要是由于湿空气密度的变化所引起的,计算结果趋势与输运模型结果趋势一致;湿度增大到50%时,温度30°的工况没有发生凝结,而温度40°的工况已发生凝结,当湿度增大到70%以后,计算达到稳定后,两种温度下均发生凝结,产生液体,空气中的水蒸气在翼型表面凝结成水膜,气动性能发生改变。
|
| 图 6 不同迎角升力系数随湿度变化曲线 Fig. 6 Variation of the lift coefficient asafunction of humidity level |
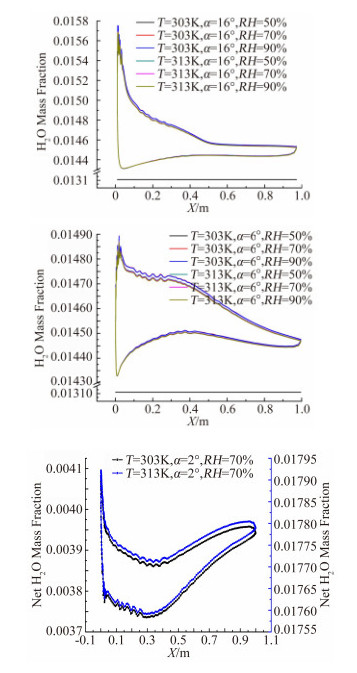
图 7是相同迎角不同湿度沿翼型表面水蒸汽质量分数分布。可以看出,两种迎角下,30°温度时,相对湿度为50%的翼型表面水蒸汽质量分数为定值,说明没有发生凝结;迎角相同,翼型表面水质量分布一致;温度相同时,相同迎角翼型的表面水蒸汽质量分数随湿度增大,净质量分数增大。湿度相同时,温度高净质量分数越大。比较净质量分数数值,发现温度对凝结的影响高于湿度对凝结的影响。
|
| 图 7 不同湿度翼型表面水蒸汽净质量分数分布 Fig. 7 Water vapor mass fraction distribution across the airfoil surface for different Relative Humidity |
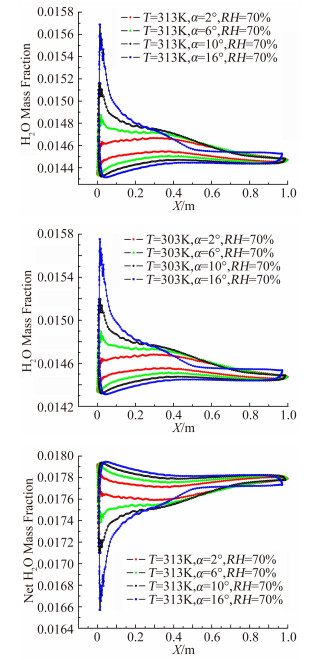
图 8是相同湿度和相同温度下不同迎角翼型表面水蒸气质量分数分布和净质量分数分布图。净质量分数是凝结前质量分数减去凝结后的质量分数。发现,两种温度下迎角越大,翼型表面水蒸气的质量分数越高。从第三张净质量分数分布图也看出,迎角越大,净水蒸气质量分数越大,说明凝结掉的水蒸气越多。
|
| 图 8 不同迎角翼型表面水蒸汽质量分数分布 Fig. 8 Water vapor mass fraction distribution across he airfoil surface for different angles of attack |
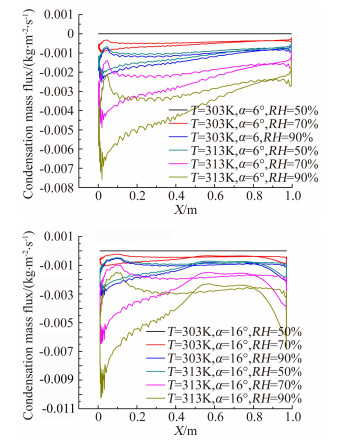
图 9为不同工况下翼型表面水蒸气的凝结质量流率。可以看出,温度相同时,相对湿度越高,凝结质量流率越大;相同湿度时,温度越高,凝结质量流率越大。靠近前缘处,凝结质量流率越大。
|
| 图 9 不同湿度翼型表面凝结质量流率 Fig. 9 Condensation mass flux across the airfoil surface for different Relative Humidity |
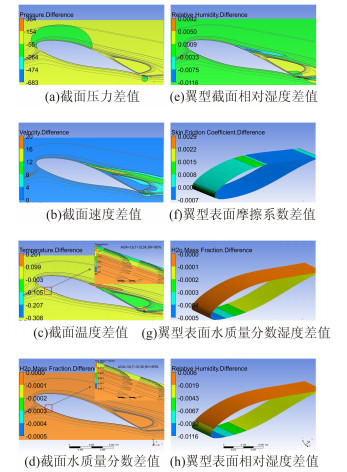
翼型上的诸多力来源于压力分布及翼型与流体的表面摩擦,表面摩擦主要形成阻力,对压力积分求得的力包括升力和阻力两个分量。因此通过分析流动参数(压力、速度等)的变化可以了解气动性能发生变化的机理。图 10为16°迎角翼型凝结前后参数差云图,此参数差为90%相对湿度下,凝结后各参数值与凝结前对应参数的差值,参数差能够反应凝结前后参数的变化情况。由图 10(a)、(b)、(c)可以看出,开启凝结模型后,整体的压力、速度和温度值增大,这些改变是凝结导致的,压力变化主要发生在翼型上表面前半部分对应的上部区域,该区域压力减小,其他大部分区域压力增大;开启凝结模型后,翼型周围绝大部区域速度值增大,增速最大区域发生在流动分离区,漩涡的外侧,速度增大的原因可能是凝结发生后,空气中的水蒸气析出,空气的粘性阻力减小,速度增大;相对应的,凝结放出热量,使翼型周围流体温度升高,且最高温度差区对应最大速度差区,同时发现,漩涡中心区温度降低。翼型截面相对湿度差分布与温度分布差相对应,最高温度差区对应于最低相对湿度差区,说明凝结发生后,水蒸气析出,放出热量,温度升高,相对湿度减小。图 10(f)、(g)、(h)为翼型表面摩擦系数差、水质量分数湿度差及相对湿度差云图,可以发现,翼型表面摩擦系数差在翼型前缘到上表面约二分之一位置处为正值,说明该表面区域凝结后,表面摩擦系数增大,其他翼型表面区域摩擦系数变小;翼型表面水质量分数差分布与相对湿度差分布近似相同,最大水质量分数差位于翼型下表面前半部分,与图 9翼型表面凝结质量流率曲线相对应;水质量分数差越大,凝结质量流率越大,凝结出的水蒸汽越多。
|
| 图 10 16°迎角翼型(T=313K, RH=90%)凝结前后参数差云图 Fig. 10 Contours of parameter difference before and after condensation at 16 degree angle of attack airfoil (T=313K, RH=90%) |
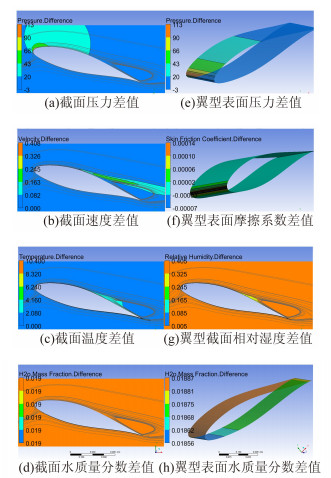
图 11为16°迎角翼型90%相对湿度与50%相对湿度的参数变量差,此变量差为开启凝结模型后,90%相对湿度下各变量与50%相对湿度下对应变量的差值,通过变量差可以了解翼型气动参数随湿度变化的趋势,有助于流动机理的了解。由图 11可以看出,随着湿度增大,流过翼型周围压力增大,对应速度增加,相对湿度增大40%,速度最大增加约0.4m/s,增速较大的区域在漩涡分离外侧区;湿度增大,温度差增大,最大温度差达到10.4℃,对应两种湿度下凝结露点温度的差值,且发生温度变化的区域为翼型上下表面层流边界层和湍流边界层,观察图 11(g)相对湿度差分布图,与温度差分布变化趋势相同,越靠近翼型表面,湿度差越小,说明凝结量越大,释放的热量越多,温度变化越大。由图 11(e)翼型表面压力差发现,翼型表面压力随湿度变化的区域主要在翼型上表面前半部分。由图 11(f)翼型表面摩擦系数差分布看出,随湿度增大,表面摩擦系数增大,且在前缘点附近增幅最大。由图 11(g)翼型表面水质量分数差分布可以看出,90%相对湿度(质量分数0.042)较50%相对湿度(质量分数0.023)上表面相差约0.01887,上表面质量分数差值较下表面大,说明上表面凝结量少,下表面凝结量多,这与图 9翼型表面凝结质量流率相对应。
|
| 图 11 16°迎角翼型(T=313K, RH=90%-50%)不同湿度参数差云图 Fig. 11 Contours of parameter difference of two humidity condition at 16 degree angle of attack airfoil (T=313K, RH=90%-50%) |
4 结 论
湿空气中的水汽凝结影响翼型的气动性能。采用组分输运模型和壁面凝结模型研究湿空气流过翼型表面的气动性能。通过求解壁面边界条件凝结组分的体积源项,实现凝结,通过预测平板表面蒸汽凝结与理论结果对比分析,验证了凝结模型的正确性。对湿空气流过翼型表面气动性能的初步研究发现,升阻力系数随湿度变化而改变,不考虑凝结时,升阻力系数随湿度增大而减小,当发生凝结时,升力系数增加。迎角不同,翼型表面凝结分布不同,翼型前缘点附近凝结量最大;相同迎角时,凝结质量流率随湿度升高增大;温度越高,凝结量越大。
湿空气凝结流动涉及复杂的相变过程,如果考虑大气中尘埃、离子等各种微小悬浮颗粒对凝结过程的影响,模型将更为复杂。因此,有必要在计算和实验两方面进一步研究凝结物理过程对翼型乃至叶片气动性能和流动的影响。
| [1] | James F C, Joseph R C, Christopher L R. Oberservation of air plane flow fields by natural condensation effects[J].Journal of Aircraft, 1989, 26(7):593–604.DOI:10.2514/3.45809 |
| [2] | Schenrr G H, Mundinger G. Similarity, drag and lift in transonic flow with given internal heat addition[J].European Journal of Mechanics-B/Fluids, 1993, 12(5):597–612. |
| [3] | Schenrr G H. Transonic aerodynamics including strong effects from heat addition[J].Computers Fluids, 1993, 22(3):103–116. |
| [4] | Li Liang, Sun Xiuling, Feng Zhenping, et al. Transonic flow of moist air around an NACA 0012 airfoil with non-equilibrium condensation[J].Progress in Natural Science, 2005, 15(9):838–842.DOI:10.1080/10020070512331343000 |
| [5] | Sun Xiuling, Li Liang, Li Guojun. Transonic flow of moist air around the ONERA M6 wing with non-equilibrium and homogeneous condensation[J].Research Journal of Applied Sciences, Engineering and Technology, 2013, 6(10):1825–1833. |
| [6] | William L W, Glenn G, Thomas J H. Aircraft-Produced Ice Particles (APIPs): additional results and further insights[J].Journal of Applied Meteorology and Climatology, 2003, 42(5):640–651.DOI:10.1175/1520-0450(2003)042<0640:AIPAAR>2.0.CO;2 |
| [7] | Jordan F L. Investigation at near-sonic speed of some effects of humidity on the longitudinal aero dynamic characteristics of a NASA supercritical wing research airplane model[R].Hampton: NASA Langley Research Center, 1972. |
| [8] | Schenrr G H, Li P. Shock wave/ boundary layer interaction with heat addition by non-equilibrium phase transition[J].International Journal of Multiphase Flow, 1993, 19(5):737–749.DOI:10.1016/0301-9322(93)90040-2 |
| [9] | Rusak Z, Lee J C. Transonic flow of moist air around a thin airfoil with nonequilibrium and homogeneous condensation[J].Journal of Fluid Mechanics, 2000, 43(1):173–199. |
| [10] | Karableas S J, Markatos N C. Water vapor condensation in forced convection flow over an airfoil[J].Aerospace Science and Technology, 2008, 12(2):150–158.DOI:10.1016/j.ast.2007.05.003 |
| [11] |
Sun Xiuling, Li Liang, Li Guojun. Numerical study of the effects of condensation of moist air on the aerodynamic characteristics of the ONERA M6 wing[J].Acta Aerodynamica Sinica, 2010, 28(2):143–148. (in Chinese) 孙秀玲, 李亮, 李国君. 湿空气凝结对ONERA M6机翼气动特性影响的数值研究[J]. 空气动力学学报, 2010, 28(2) : 143–148. |
| [12] |
Sun Xiuling, Li Liang, Li Guojun. Numerical investigation of moist air flow with non-equilibrium condensation around airfoils[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(8):1546–1551. (in Chinese) 孙秀玲, 李亮, 李国君. 翼型湿空气非平衡凝结流动的数值研究[J]. 航空学报, 2010, 31(8) : 1546–1551. |
| [13] | Franck B, Niels S, Jeppe J. Wind turbine airfoil catalogue[R]. Roskilde: Risø National Laboratory, 2001. |
| [14] | Sparrow E M, Minkowycz W J, Saddy M. Forced convection condensation in the presence of noncondensables and interfacial resistance[J].International Journal of Heat and Mass Transfer, 1967, 10(12):1829–1845.DOI:10.1016/0017-9310(67)90053-1 |
| [15] | Bell B. Application Brief: Film Condensation of Water Vapor[R]. Lebanon, 2003. |


