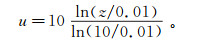2. 长安大学 公路学院, 陕西 西安 710064
2. School of High way, Chang'an University, Xi'an 710064, China
正如风洞试验需要在风洞内重现充分发展的大气边界层,在计算风工程中,构建水平均一的(horizontally homogenous)大气边界层是保证数值模拟结果准确可靠的关键前提。所谓水平均一,是指来流物理量沿流向梯度为0,即计算域入口处的来流在无干扰条件下到达出口保持不变。这样的边界层可称为平衡边界层。构建平衡边界层,需要来流边界、湍流模型和壁面条件三者相互协调。由于问题十分复杂,通常难以给定一个既能满足理论要求,还能与场地实测数据相符的来流边界条件,因此在数值模拟中实现平衡大气边界层十分不易。
边界层在计算域入口段产生的物理量变化,将与结构物对来流的扰动作用叠加,共同体现在计算结果中。同时,边界层的物理量变化,将使得作用在结构物上的风剖面与入口处的预设条件不符。两种效应降低了数值模拟的可靠性与准确性。
对于如何构建平衡大气边界层的问题,诸多学者进行了研究。Blocken[1]等指出入口风速剖面中包含的粗糙长度应该与壁面函数相匹配,否则来流在计算域内将发展成一个新的平衡边界。然而仅按照其建议的方法修改壁面参数,来流在计算域内依然发生变化。Richards和Hoxey[2](1993)从标准k-ε模型方程出发,基于对平衡大气边界层的一系列假设,推导出一组边界条件及其相应的模型常数,但是其给出的湍动能剖面只能是常数,与实际不符。在此基础上,Yang[3]等推导出标准k-ε模型方程的通解,给出了一组符合实测的边界条件,但Yang没有给出模型常数设置方法,给出的边界方程不能直接得到相应的模型常数。
本文首先对Richards与Yang提出的两类边界条件进行理论对比。然后应用两种方法,对《公路桥梁抗风规范》(JTG-TD60-01-2004)中建议的A类风场进行足尺数值模拟[4]。通过对两个算例结果的比较,分析了两类边界条件的差异及各自的适用条件。根据模拟结果,本文对模型常数和边界条件做了调整,改善了平衡大气边界层的模拟结果。
1 平衡大气边界层的边界分析 1.1 第一类边界条件定常流的标准k-ε模型控制方程为:
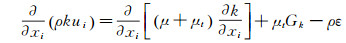 (1)
(1) 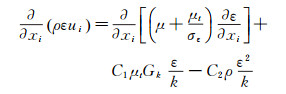 (2)
(2) 式中,湍流粘性的定义为:
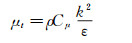 (3)
(3) Richards与Hoxey(1993)首先对平衡大气边界层做了以下假设:(1)边界层内竖向速度为0,对于二维流场,有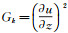
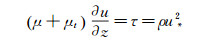 (4)
(4) 其中,τ为大气内部切应力,u*为剪切速度。在大气边界层局部区域内,该假设近似成立。
其次,研究者对计算域入口处的平均风速剖面使用对数律表达式拟合:
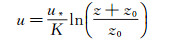 (5)
(5) 式中K为冯卡门常数,通常取值为0.4~0.42。
在风速u、湍动能k与湍流耗散率ε水平方向梯度为0的条件下,由方程(1)可以得到μtGk=ρε,即:
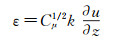 (6)
(6) 由于μ远小于μt,可将其忽略。将方程(3)~(5)联立求解,不难得出Richards等建议的入口湍动能k及其耗散率ε表达式:
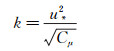 (7)
(7) 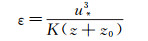 (8)
(8) 这组由k-ε湍流模型方程(1)推导出的边界条件表达式(5)、(7)和(8)自然能够满足方程(1)。再将其代入模型方程(2)中,要使得方程成立,模型常数需满足关系式:
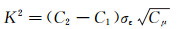 (9)
(9) 第二类边界条件由Yang等推导,没有使用方程(4),而是将方程(3)、(5)和(6)直接代入到方程(1)中得到:
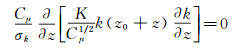 (10)
(10) 可以导出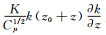
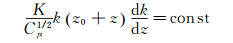 (11)
(11) 分离变量后得该微分方程通解:
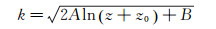 (12)
(12) 代入方程(6)得到:
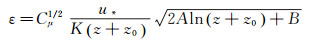 (13)
(13) 方程(5)、(12)和(13)就是Yang等建议的入口边界条件。
将方程(5)、(6)和(8)代入到方程(2)中,方程左边为0,而方程的右边:
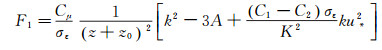 (14)
(14) 可见Yang推导的边界条件没有直接对标准k-ε湍流模型中的常数关系进行限制,但在入口边界条件确定后应验算F1是否为0。若F1不等于0,则模型方程(2)不能满足,来流将在计算域内发展成一个满足模型方程的新边界层。
1.3 两类边界条件对比从以上两类边界条件的推导过程可以看出,二者的最大差异在于是否假设边界层内切应力相等。该假设仅在大气边界层的小范围内近似成立,与真实情况略有出入。使用该假设,引入方程(4),使得第一类边界条件中的湍动能k沿高度方向保持不变,与实际大气边界层不符。但第一类边界条件中,平均风速剖面中的剪切速度u*物理意义明确,湍动能耗散率ε表达式简单,同时标准k-ε模型中的常数也有确定的关系。
第二类边界条件没有使用方程(4),而是使用与第一类边界条件相同的平均风速剖面表达式,推导出标准k-ε模型控制方程(1)的通解(9)。该解能够通过改变算式中的参数A和B,拟合湍动能k随高度变化的数值,使得计算域入口的湍动能设置更接近实际情况。然而这样的改进也引来新问题:将方程(2)整理后得到的等式
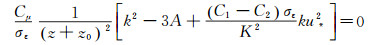 (15)
(15) 并不能得出确定的模型常数关系。此外,将方程(3)、(6)代入切应力表达式(4),得到:
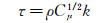 (16)
(16) 由此可以看出,随着湍动能k沿高度的变化,大气边界层内的水平方向切应力沿竖直方向的分布是变化的。因此,平均风速剖面表达式中的u*值也应沿高度变化。
2 算例验证 2.1 风场参数确定按照我国《公路桥梁抗风规范》推荐的A类风场设置计算域入口平均风速剖面与湍动能剖面。
首先假定风速的参考高度为10m,设该高度处的风速为10m/s,则A类风场的平均风速剖面为:
“规范”中只给出A类风场不同高度的流向湍流强度,需要换算才能得到相应的湍动能剖面。在只关心流向湍流强度的前提下,可进一步假定竖向脉动风速为0,按关系式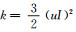
| z | u | I | k |
| 10 | 10.00 | 15% | 3.38 |
| 20 | 11.00 | 14% | 3.56 |
| 30 | 11.59 | 13% | 3.41 |
| 40 | 12.01 | 12% | 3.11 |
| 50 | 12.33 | 12% | 3.28 |
| 70 | 12.82 | 11% | 2.98 |
| 100 | 13.33 | 11% | 3.23 |
| 150 | 13.92 | 10% | 2.91 |
| 200 | 14.34 | 10% | 3.08 |
2.2 入口边界条件设置
取冯卡门常数K=0.42,则剪切速度u*=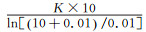
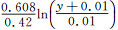
第一类边界条件中的湍动能k值只能为常数,这里取k=3.4,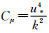
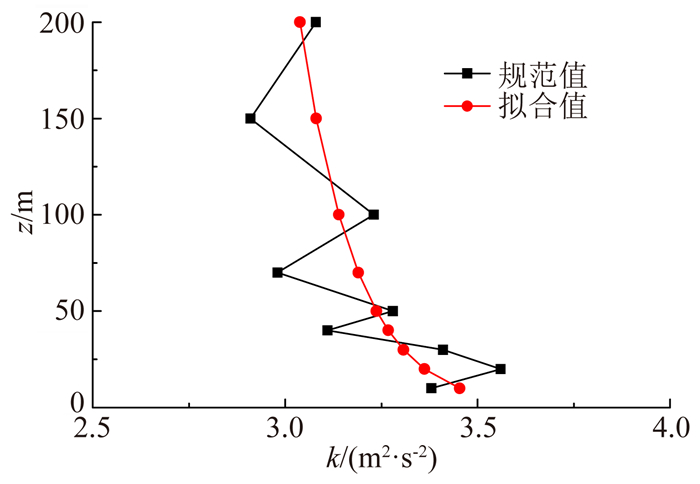
在第二类边界条件中,湍流强度剖面拟合的表达式为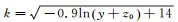
|
| 图 1 湍流强度拟合结果 Fig. 1 Turbulence intensity fitting results |
模型常数取值与第一类边界条件相同,得到湍动能耗散率剖面为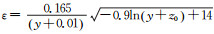
| 第一类边界条件 | 第二类边界条件 | |
| 平均风速 u | 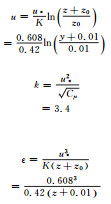 | 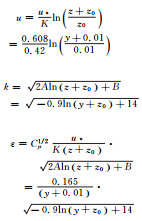 |
| 湍动能 k | ||
| 湍动能耗 散率ε |
2.3 计算模型
采用二维模型验证两类边界条件的适用性,矩形计算域大小为400m×5000m(y×x),计算域中不设置任何结构物。采用结构化网格对计算域进行离散,水平向网格间距为10m,竖向首层网格高度取0.32m,渐变率1.08,首层网格中心高度zp=0.16m。网格总数为60 000。采用SIMPILEC算法求解,对流项的离散格式选用QUICK。以各物理量的无量纲残差低于10-5为计算收敛标准。计算平台为Fluent6.2。
2.4 壁面函数及其他参数设置locken[1]与Richards[5]均指出,壁面函数中粗糙高度Ks与边界层粗糙长度z0并不相等。二者之间的关系需由平均风速剖面,湍动能剖面与壁面函数三者共同确定。
Fluent中标准壁面函数[6]为:
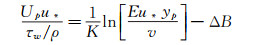 (17)
(17) 式中,Up为首层网格中心高度处平均风速;yp是首层网格中心高度;v是动力粘度,取值为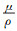
;Cs为壁面粗糙常数;u*为剪切速度,等于Cμ1/4kp1/2;E为经验常数,约取9.793。Ks+=u*Ks/v,Ks+>90时,
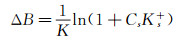 (18)
(18) 壁面剪切速度:
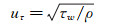 (19)
(19) 在平衡大气边界层中u*=uτ。此时壁面函数表达式为:
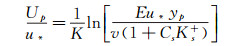 (20)
(20) 又由于CsKs+>>1,将方程(5)代入,整理得:
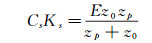 (21)
(21) 设Cs=1,可以得到Ks=0.092。
第二类边界条件中的平均风速剖面的形式虽然与第一类边界条件相同,但剪切速度u*在不同高度取值不同。首层网格中心高度处的实际摩擦速度应为u′*=Cμ1/4kp1/2=0.671,代入方程(20),整理得:
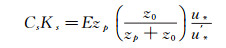 (22)
(22) 设Cs=1,解得Ks=0.122,即为第二类边界条件的壁面参数。
此外,应该注意到空气分子粘性μ=1.71×10-5Ns/m2,空气湍流粘性为:
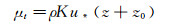 (23)
(23) 按照第一类边界条件,在计算域顶部,μt=125Ns/m2。湍流粘性比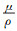
其他模型常数为C1=1.5,C2=1.92,σk=1。
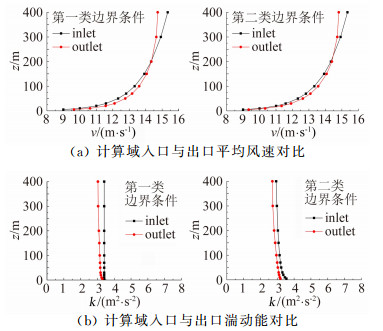
2.5 计算结果使用两类边界条件计算得到的入口与出口平均风速和湍动能的对比如图 2所示。
|
| 图 2 两类边界条件计算结果对比 Fig. 2 Comparison of two kinds of boundary conditions calculation results |
图 2(a)表明,使用两类边界条件计算得到的出口与入口平均风速剖面相差较小。在计算域顶部,出口平均风速低于入口设定,这主要是受计算域顶面的边界条件影响,可以通过在顶面施加剪应力而改善[7-8]。在计算域底部,出口处平均风速均略高于入口设定,且第二类边界条件计算得到的平均风速改变量小于第一类边界条件。这是由于第二类边界条件在地面附近设置的湍动能值高于第一类边界条件,由此推算出的壁面Ks值更高导致的。方平治[9]讨论了Ks对平均风速剖面的影响,从中可以看出,增大Ks值能够减小计算域底部平均风速剖面沿高度方向的梯度。图 2(b)表明使用两类边界条件计算得到的出口处湍动能要小于出口处的设置值。同样,使用第二类边界条件湍动能的改变量略小于第一类边界条件。
比较两个算例可以看出,使用两类边界条件得到的计算结果都能近似满足构建平衡大气边界层的要求。第一类边界条件的设置方法较简单便捷,但湍动能的设置与实测结果有偏差,仅适宜在湍动能沿高度变化小的情况下使用。第二类边界条件可以设置湍动能沿高度的变化,更接近实际风场。而且地面附近区域设置的湍动能值更大,也使得壁面Ks增大,从而减小了计算域底部平均风速剖面沿高度方向的梯度,与入口平均风速剖面更加吻合。因此,第二类边界条件适宜在计算准确性要求更高及湍动能强度随高度变化大的情况下使用。
3 对第二类边界条件的改善为得到更加平衡的大气边界层,针对第二类边界条件得到的湍动能偏小的情况,本文首先从满足模型控制方程(2)的要求入手,对F1是否为0进行验算。从算式(14)可以看出,F1在z较小的壁面附近数值较大,减小C1将减小F1值,因此可以适当修改C1改善计算结果。
Durbin[10]指出C1合理取值应为:
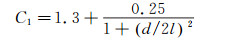 (24)
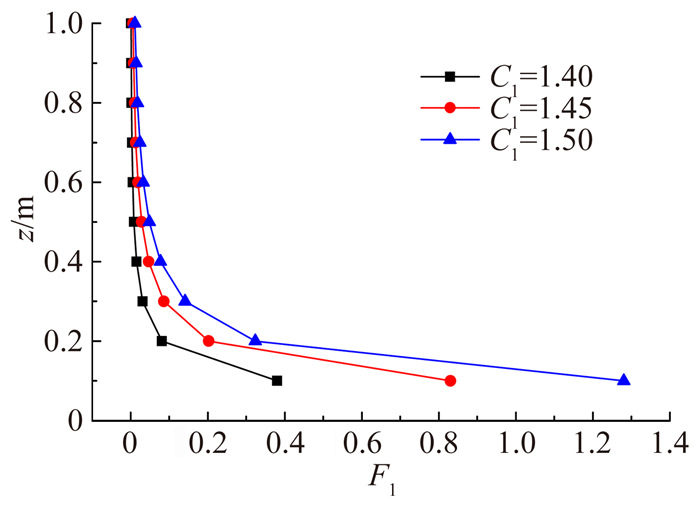
(24) 其有效取值范围在1.3~1.55之间。在不改变边界条件与其他模型常数的前提下,本文尝试修改C1=1.45与C1=1.40。C1不同取值时F1的数值如图 3所示。
|
| 图 3 不同C1取值时F1的数值 Fig. 3 F1 values with diffirent C1 |
图 3表明,随着C < 1的减小近壁面位置F1更接近0。不同C1取值得到的计算结果如图 4所示。
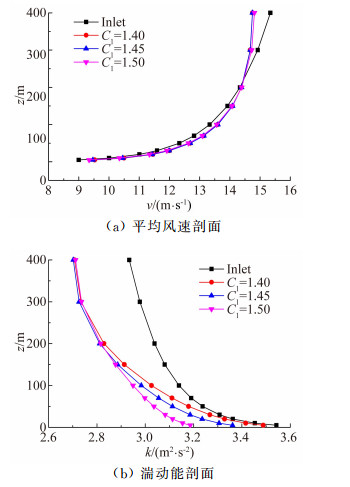
|
| 图 4 C1值计算结果 Fig. 4 Calculation results with diffirent C1 |
从计算结果可以看出,随着常数C1的降低,平均风速的取值几乎没有变化。而湍动能的变化有其特点:高空位置(>200m)的湍动能差异微小,而200m以下位置的湍动能值随着C1的降低而增大,越接近壁面,增大的数值越多。
为减少高空位置湍动能的衰减,本文尝试修改其他边界条件。注意到即便是第一类边界条件,当标准k-ε湍流模型两个控制方程完全满足平衡大气边界层条件时,来流物理量经过计算域后依然发生变化。这是由于边界条件的前提假定与计算域内的实际流场的微小差异引起。这样的误差难以预估,因此,鉴于以上模拟结果显示湍动能在出口处小于入口值,本文尝试将入口处的湍动能耗散率剖面表达式上增加一个系数,使得
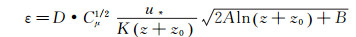 (25)
(25) D分别取0.9、0.8和0.7,得到的计算结果如图 5所示。
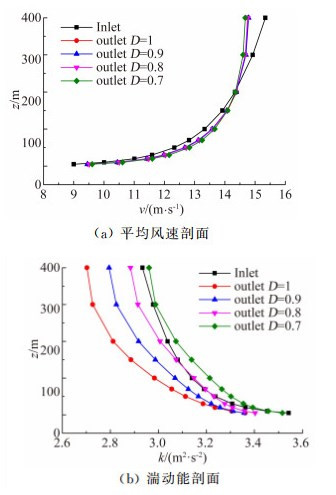
|
| 图 5 不同D值计算结果 Fig. 5 Calculation results with diffirent D |
从图 5可以看出,计算域入口处设置湍动能耗散率的变化同样不影响出口位置平均风速值,而且对出口位置全部高度范围内的湍动能值都有影响。具体表现为:在入口处湍动能耗散率减小的同时,出口处的湍动能值在全部高度范围内都有增加,但增加的数值并不相同。高处的湍动能增加值较大,越接近壁面增加值越小。D取0.7时,高空处的湍动能与入口条件吻合度较好,但在200m以下低风速位置湍动能值高于入口值。D取1与0.9时,出口处湍动能仍小于入口值。取D=0.8时,计算域出入口的湍动能吻合度较好。
4 结论本文首先分析了两类平衡大气边界层的入口边界条件,并通过算例验证了其准确性与适用性。进而对边界条件中的参数进行了研究,以期改善数值模拟结果。总结全文,得出如下结论:
1) 第一类边界条件的设置方法相对简单,但湍动能为定值,只适宜在湍动能沿高度分布均匀的大气边界层模拟中使用。第二类边界条件的设置方法较复杂,但允许湍动能沿高度变化分布,在大气边界层模拟中的适用范围广泛。
2) 减小C1会增大计算域内壁面附近位置的湍动能,但不影响高空处湍动能。同时C1对平均风速剖面影响微小。
3) 减小ε能增大计算域内的湍动能值,效果随高度的增大而增加。ε对平均风速剖面影响微小。
| [1] | Blocken B, Stathopoulos T, Carmeliet J. CFD simulation of the atmospheric boundary layer: wall function problems[J].Atmos. Environ., 2007, 41(2):238–252.DOI:10.1016/j.atmosenv.2006.08.019 |
| [2] | Richards P J, Hoxey R P. Appropriate boundary conditions for computational wind engineering models using the k-ε turbulence model[J].Journal of Wind Engineering and Industrial, 1993, 46-47:145–153.DOI:10.1016/0167-6105(93)90124-7 |
| [3] |
Yang Wei, Gu Ming, Chen Suqin. A set ofturbulence boundary condition of k-ε model for CWE[J].Acta Aerodynamica Sinica, 2005, 23(1):97–102. (in Chinese) 杨伟, 顾明, 陈素琴. 计算风工程中k-ε模型的一类边界条件[J]. 空气动力学学报, 2005, 23(1) : 97–102. |
| [4] |
JTG/TG-T D 60-01-2004, Wind-resistant design specification for highway bridges[S]. JTG-/T D 60-01-2004, 公路桥梁抗风设计规范[S]. |
| [5] | Richards P J, Norris S E. Appropriate boundary conditions for computational wind engineering models revisited[J].J. Wind Eng. Ind. Aerodyn., 2011, 99:257–266.DOI:10.1016/j.jweia.2010.12.008 |
| [6] | Fluent 6.1 Documentation[R]. Fluent Inc. 2003. |
| [7] |
Yang Wei, Jin Xinyang, Gu Ming, et al. A study on the self-sustaining equilibrium atmosphere boundary layer in computational wind engineering and its application[J].China Civil Engineering Journal, 2007, 40(2):1–5. (in Chinese) 杨伟, 金新阳, 顾明, 等. 风工程数值模拟中平衡大气边界层的研究与应用[J]. 土木工程学报, 2007, 40(2) : 1–5. |
| [8] | Hargreavesa, D M, Wright N G. The use of commercial CFD software to model the atmospheric boundary layer[C]//The Fourth International Symposium on Computational Wind Engineering, Yokohama, Japan, 2006: 797-800. |
| [9] |
Fang Pingzhi, Gu Ming, Tan Jianguo. Numerical wind fields based on the k-ε turbulent models in computational wind engineering[J].Chinese Journal of Hydroynamics, 2010, 25(4):475–483. (in Chinese) 方平治, 顾明, 谈建国. 计算风工程中基于k-ε系列湍流模型的数值风场[J]. 水动力学研究与进展, 2010, 25(4) : 475–483. |
| [10] | Durbin P A. Separated flow computations with the k-ε-v2 model[J].AIAA Journal, 1995, 33(4):659–664.DOI:10.2514/3.12628 |
| [11] | Svetlana Poroseva, Gianluca Iaccarino. Simulating separated flow using k-ε model[R]. Annual Research Briefs 2001, Center for Turbulence Research, Standford University, 2001: 375-383. |
| [12] | Yang Yi, Gu Ming, Chen Suqin, et al. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering[J].J. Wind Eng. Ind. Aerodyn., 2009, 97(2):88–95.DOI:10.1016/j.jweia.2008.12.001 |
| [13] |
Zeng Kai, Wang Congjun, Huang Bencai, et al. Suggestion and analysis of several key factors in computational wind engineering[J].Acta Aerodynamica Sinica, 2007, 25(4):504–508. (in Chinese) 曾锴, 汪丛军, 黄本才, 等. 计算风工程中几个关键影响因素的分析与建议[J]. 空气动力学学报, 2007, 25(4) : 504–508. |
| [14] | Launder B E, Spalding D B. The numerical computation of turbulent flows[J].Computer Methods in Applied Mechanics and Engineering, 1974, 3(2):269–289.DOI:10.1016/0045-7825(74)90029-2 |
| [15] | O'Sullivan J P, Archer R A, Flay R G J. Consistent boundary conditions for flows within the atmospheric boundary layer[J].J. Wind Eng. Ind. Aerodyn, 2011, 99(99):65–77. |